一种模糊PID控制器的设计与仿真
黄良沛, 邹东升, 陈磊, 王岳峰
(湖南科技大学a.机械设备健康维护湖南省重点实验室;b.机电工程学院,湖南湘潭411201)
0 引言
PID控制技术是工业过程控制中最广泛使用的控制技术[1-15],PID控制技术建立在被控对象具有精确数学模型(传递函数和状态方程)的基础上[16],采用PID控制对被控对象进行控制时,通过调节PID控制器的3个控制参数Kp、Ki、Kd来获得期望的控制效果。被控对象的数学模型精确,PID控制的控制效果较好。对于难以建立精确数学模型的复杂系统,PID控制的控制效果不理想。模糊控制在求解复杂系统时不依赖精确的数学模型,能实现参数的自适应调整,结合PID控制与模糊控制的模糊PID控制技术,具有模糊控制的参数自适应调整与PID控制技术控制精度高的优点,将模糊PID控制技术用于难以建立精确数学模型的复杂系统能获得较好的控制效果,模糊PID控制器不依赖于精确的数学模型[17]对被控对象求解,而根据控制规则对PID控制参数实行自调整来获得较好的控制效果,适用于复杂系统等建模不准确的系统。本文介绍了模糊PID控制器的工作原理及参数自整定调整的原理;确定了模糊PID控制器的模糊论域与隶属度函数;制订了模糊PID控制器的控制规则;设计了一种模糊PID控制器并以二阶系统作为测试系统,考虑加入干扰的影响,以模糊PID控制器与常规PID控制器同时对系统进行控制,并对两者的控制性能进行对比分析性能,分析结果更具有意义。
1 模糊PID控制器的设计
1.1 模糊PID控制器的工作原理
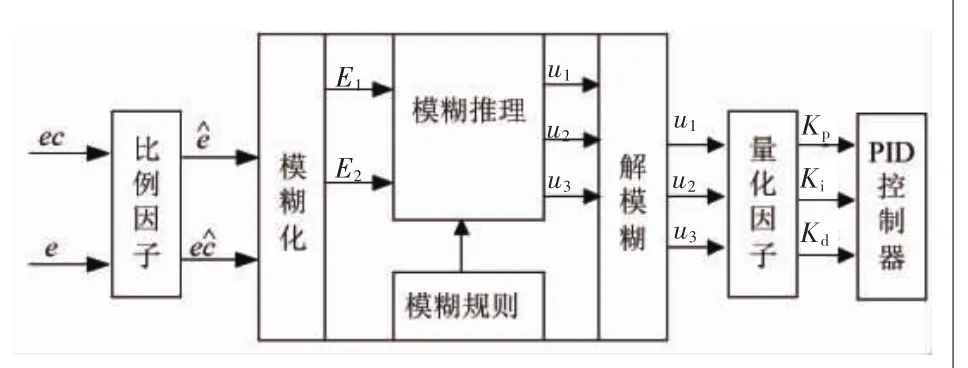
图1 模糊PID控制器结构示意图
模糊PID控制器的输入为误差e和误差变化率ec,误差为反馈值与控制设定值通过对比所得,输出为PID的三个调节参数Kp、Ki、Kd。控制器工作时,首先通过比例因子Ke和Kec将误差和误差变化率转化到标准值e^、ec^∈[-1,1],再经过模糊化处理将标准值e^、ec^生成模糊变量E1、E2,然后基于Mamdani算法和模糊推理规则求解出U1、U2、U3。最后经过解模糊方法(如最大隶属度法,加权平均分等)得到标准化u^1、u^2、u^3再乘以相对应的量化因子k1、k2、k3即得到PID调节值Kp、Ki、Kd。将调节值传入控制器即可对被控对象实行控制。模糊PID控制器结构如图1所示。
1.2 模糊PID控制器的论域与隶属度函数
设定模糊推理的输入e和ec的论域均为 {-3,-2,-1,0,1,2,3},对应的语言值为{负大(NB),负中(NM),负小(NS),零(ZO),正小(PS),正中(PM),正大(PB)},采用的隶属度函数均为三角形(trimf);设定模糊推理的输出Kp、Ki、Kd的论域均为{1,2,3,4},对应语言值{零(ZO),正小(PS),正中(PM),正大(PB)},采用的隶属度函数为三角形(trimf),Z型(zmf)和S型(smf)三种。模糊推理使用隶属度函数的大小表征误差的大小,影响模糊PID控制器输出的PID调节值的大小。
1.3 模糊PID控制器的控制规则
模糊控制规则是模糊PID控制器中最重要的一部分,决定着模糊PID控制器的控制精度与控制性能。在系统处于不同的e和ec值时,为了获得好的控制结果,需要设定以下模糊控制规则:当误差e的绝对值与误差变化率ec的绝对值较大时(误差语言值为正大或正中,对应论域分别为±3,±2),为了降低调整时间,初始Kp调节值要取较大值(Kp语言值为正大,对应论域为4);为了保证系统在可控范围内,Kd值应该较小(Kp语言值为0,对应论域为1);为了防止控制过程中系统出现较大的超调量,应限制积分环节,Ki取值应该极小(Ki语言值为正小,对应论域为2。当误差e的绝对值与误差变化率ec的绝对值适中时(误差语言值为正中或正小,对应论域分别为±2、±1),为了降低超调,Kp值应稍微降低(Kp语言值为正大,对应论域为4);系统响应速度取决于Kd的取值,此时Kd值应适中(Kd语言值为正小或正中,对应论域分别为2、3)。同时为了增强控制效果,Ki值不宜太大(Ki语言值为正小或零,对应论域分别为2、1)。当误差e的绝对值与误差变化率ec的绝对值较小时(误差语言值为正小或零,对应论域分别为±1、0),为了获得好的稳态性能,取较大的Kp(Kp语言值为正大,对应论域为4),Ki(Ki语言值为正大,对应论域为4);此时系统可能出现振荡现象,为防止出现这种现象,当e的绝对值与误差变化率ec的绝对值趋向于减小,Kd取较大值(Kp语言值为正大,对应论域为4),当e的绝对值与误差变化率ec的绝对值趋向于增大,Kd取较小值(Kp语言值为零,对应论域为1)。根据以上分析,可以总结出Kp、Ki、Kd的自调整规则,如表1所示。
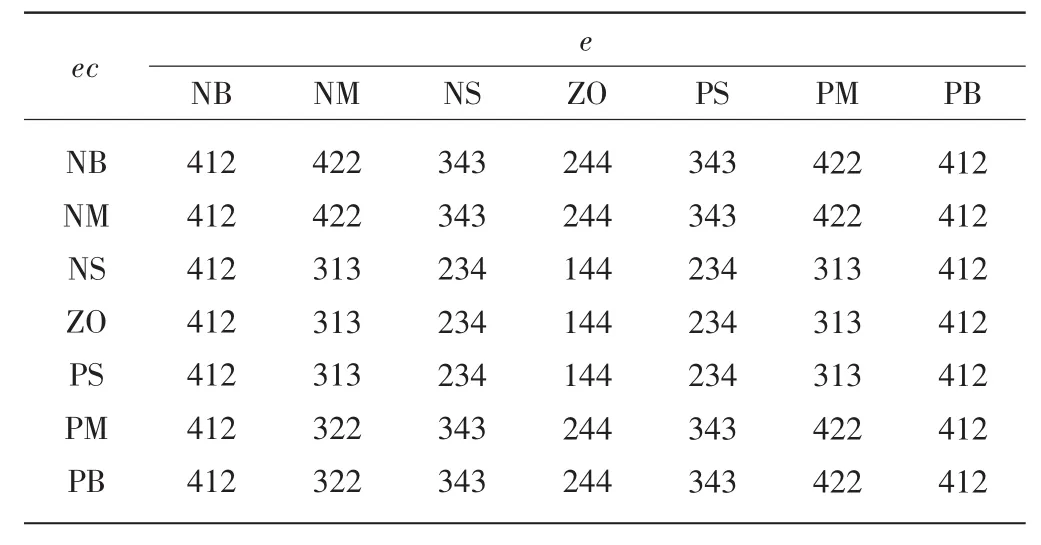
表1 模糊PID控制规则中Kp、Ki、Kd值查询表
根据模糊PID控制器的隶属度函数、论域及控制规则查询表,可在MATLAB软件中的fuzzy工具箱生成模糊PID控制器,生成的模糊PID控制器为两输入,三输出系统,包含49条模糊规则。输入变量e、ec的隶属度曲线如图2所示,输出变量Kp、Ki、Kd的隶属度曲线如图3所示。
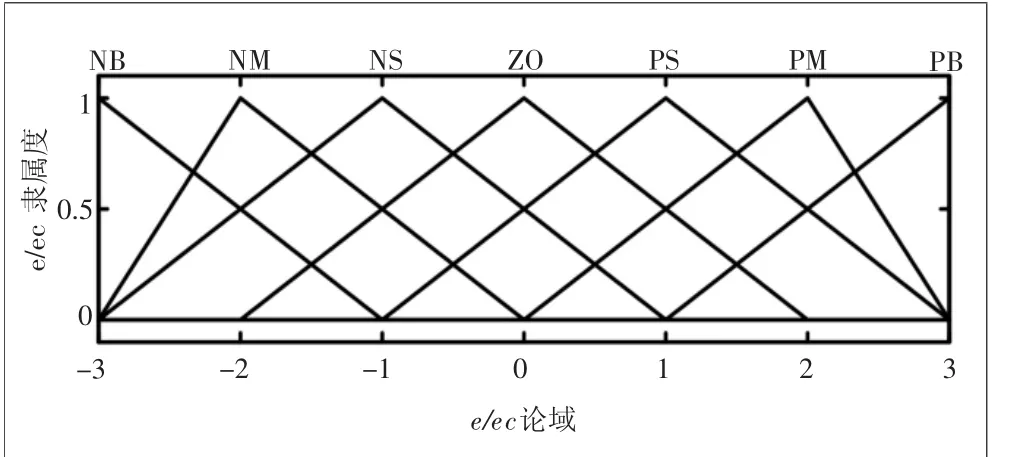
图2 输入变量隶属度曲线
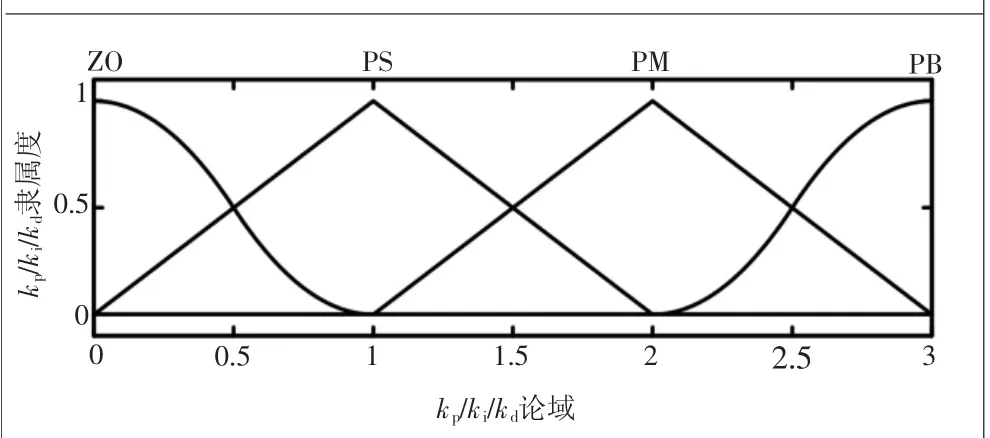
图3 输出变量隶属度曲线
1.4 模糊PID控制器参数自整定原理
由表1可知:模糊PID控制器的调整参数由三个参数决定:e,ec的绝对值对应的论域和PID控制参数的论域。设定某时刻e,ec的绝对值|e|、|ec|已知。根据表1,可写出PID调节器中Kp对应的每条调整规则,如第一条可写为:R1:if|e|=NB and |ec|=NB then Kp=PB。
该条规则隶属度计算公式为
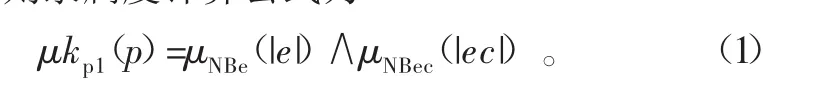
式中:μNBe(|e|)表示误差e对应语言值为NB时的隶属度函数,μNBc(|ec|)表示误差变化率ec对应语言值为NB时的隶属度函数;同理可求出Kp的其他所有规则的隶属度μkpi(p)(i=1,2,3···,n),其中,n为Kp的总规则条数,pi为第i条规则中Kp所取论域的中心值。
Kp调整值的计算公式为
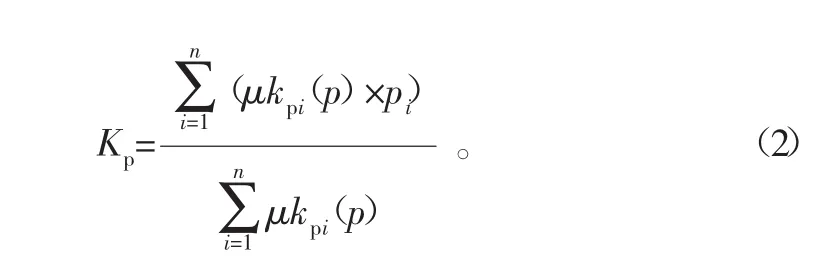
同理可以得出Ki,Kd的计算公式,其中μkIi(I)(i=1,2,3···,n) 为Ki所有规则的隶属度,l为Ki的总规则条数,Ii为第i条规则中Ki所取论域的中心值;μkdi(D)(i=1,2,3···,n)为Kd所有规则的隶属度,其中n为Kd的总规则条数,Di为第i条规则中Kd所取论域的中心值。计算公式如下所示:
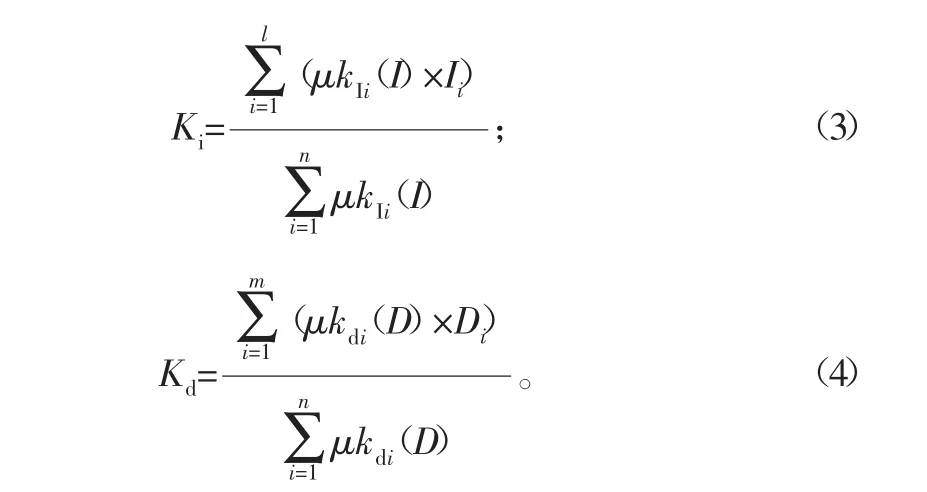
由式(1)~式(4)中可知,Kp、Ki、Kd调整值与误差、误差变化率之间存在着函数关系,满足了系统在不同e、ec状态下对PID控制参数的调节需要。在MATLAB软件中的fuzzy工具箱可查看模糊PID控制器在不同误差和误差变化率下的PID控制参数调整值,下面列举一些在不同误差和误差变化率下的PID控制参数调整值。误差隶属度为0.5,误差变化率隶属度为0时,Kp调整值为1.1,Ki调整值为1.92,Kd调整值为1.58。误差隶属度为1.5,误差变化率隶属度为0时,Kp调整值为1.5,Ki调整值为1.48,Kd调整值为1.53。误差隶属度为0,误差变化率隶属度为0.5时,Kp调整值为1.12,Ki调整值为2.2,Kd调整值为1.7。误差隶属度为0,误差变化率隶属度为1.5时,Kp调整值为1.25,Ki调整值为2.2,Kd调整值为1.72。由以上数据可知控制参数是实时调整的,满足了系统在不同e,ec状态下对PID控制参数的调节需要。
2 模糊PID控制器建模与仿真分析
2.1 模糊PID控制器建模
在MATLAB/simulink仿真软件下建立系统仿真模型,模型主要由模糊PID控制器,干扰信号,被控系统(被控对象),控制设定值等组成,如图4所示。
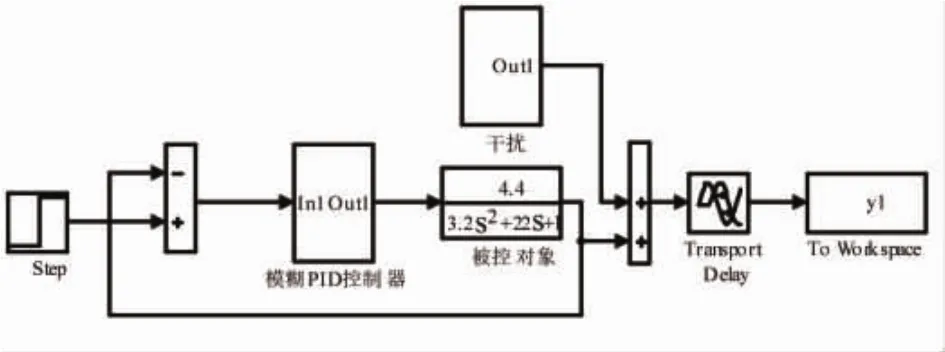
图4 仿真模型
2.2 模糊PID控制器仿真分析
选择二阶系统G(S)=4.4/(3.2S2+22S+1)作为被控系统进行仿真,测试信号为单位阶跃信号,分别在无干扰和加入随机干扰条件下进行仿真,仿真结果分别如图5、图6所示。
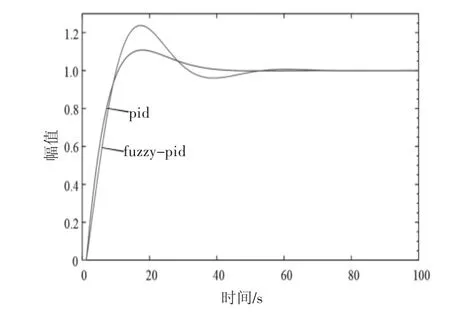
图5 无干扰仿真结果
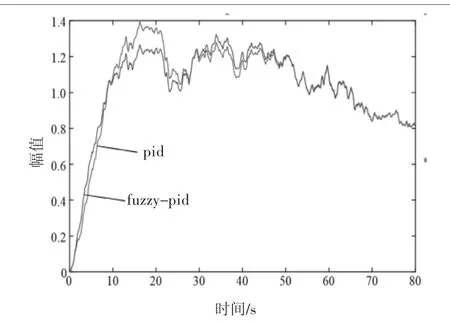
图6 有干扰仿真结果
测试信号为单位阶跃信号,即控制设定值的大小为1。将图5进行处理后可以得到以下结论:在无干扰条件下,在模糊PID控制器控制下,系统的调整幅值峰值为1.08,经计算可知其超调量为8%;调整时间为41 s。常规PID控制下,系统的调整幅值峰值为1.25,经计算可知其超调量为24%,调整时间为72 s。在两种控制器控制下,系统的响应时间相差不大。在有干扰条件下,模糊PID控制器的控制效果也要优于常规PID控制器的控制效果。

