基于改进Canny算子的脑部MR图像分割算法的研究

曲蕴慧，弓明，廖尹坤，王鑫，扬伍连

西安医学院 a. 计算机教研室；b. 医学技术学院，陕西 西安 710021

引言

随着医学成像技术的不断提高以及核磁共振（MR）技术在临床医学领域的广泛使用，医学核磁共振图像数量不断增多，给医生浏览判读带来了巨大的工作量，导致医生视觉疲惫，不可避免地发生误判。随着计算机视觉技术以及图像处理算法的发展，借助医学图像处理与分析手段不仅可以减轻由于图像过多而使医生解读费时的压力，同时极大地提高了医生诊疗水平，从而为医学研究的进一步发展提供了坚实的基础[1]。

在医学图像处理与分析领域，医学图像分割是对医学图像进行进一步处理和分析的基础。图像分割就是把医学图像分成若干个特定的、具有独特性质的区域并提取感兴趣目标的技术和过程。由于MR图像的多样性和复杂性，以及目前核磁共振设备成像技术上的特点，使得MR图像存在一定的噪声， MR图像的分割更加困难[2]。

本文针对传统的Canny算子在脑部MR图像分割时存在的易受噪声干扰等问题，提出改进的Canny 算子，并将其运用于脑部MR图像分割中，实验结果证明，改进后的Canny算子能够有效地检测出对象边缘，并对MR图像中常见噪声有很强的鲁棒性。

1 传统Canny算子

Canny算子是John F. Canny 于1986 年提出的一种经典的边缘检测算法，具有信噪比大，检测精度高等优点，在很多领域都有非常广泛的应用[3]。传统Canny算法流程，见图1。

图1 传统Canny算子算法流程图

1.1 图像平滑

传统Canny算子利用Gaussian滤波器对图像进行平滑处理。Gaussian平滑滤波器是将输入图像的每一个像素点与高斯内核进行卷积运算，将卷积和作为输出图像该像素点的像素值。Gaussian平滑滤波器的输出是邻域像素的加权平均，离中心越近，像素权重越高[4]。

Gaussian滤波函数如式(1)所示：

其中，σ为图像的标准差。二维Gaussian函数的示意图，见图2。

图2 二维Gaussian函数

1.2 计算梯度的幅值和方向

梯度的计算是Canny算子最核心的环节。设G是式(1)所示的2D高斯函数，将原图像为f(x，y)与算子Gn做卷积，Gn是G沿n方向的一阶方向导数，如式(2)所示：

对于图像f(x,y)，边缘的法向n如式(3)所示：

1.3 对梯度幅值进行非极大值抑制

为了防止所得的边缘点太过于密集、出现部分伪边缘的情况，传统Canny算子在每个像素点使用3×3的模板进行非极大值抑制，去掉伪边缘点。

图像的边缘位于Gn与图像f卷积在n方向上的局部最大值位置处，有式(4)成立：

将式(2)代入式(4)，可得非极大值抑制算子，如式(5)所示：

1.4 双阈值方法检测连接边缘

由于噪声引起的单个边缘的虚假响应会造成边缘轮廓断开的情形，这种问题可以通过滞后阈值化来消除。故在传统Canny算子中，认定所有灰度大于高阈值的点为边缘点；灰度在高低阈值之间的点，如果周围有大于高阈值的像素则认定该点也是边缘点；灰度小于低阈值的点不是边缘点[5]。

1.5 传统Canny算子的缺点

（1）传统Canny算子采用高斯函数对图像做平滑处理，因此具有一定的抑制噪声的能力，可以用于一些边界较光滑、受噪声污染小的医学图像的边缘检测，但对于受伪影影响的脑部MR图像，会将一些高频边缘平滑掉，造成边缘丢失。

（2）传统Canny算法对阈值选取比较敏感，如果Canny算子的高阈值选取过大，则会丢失灰度值变化较小的边缘；阈值选取过小则会造成细节过多，增加伪边缘数目。此外，如果一个点的灰度处于高低阈值之间，又与边缘点相邻，则被认定为边缘点，这样检测得到的边缘往往较厚，很难达到单像素级[6]。

2 改进的Canny算子

本文针对传统Canny算法应用于脑部MR图像分割时所产生的两方面问题，对传统的Canny算子进行了改进。

2.1 对图像平滑方法的改进

传统Canny算子采用高斯函数进行平滑滤波处理，但对于MR图像中的伪影（如运动伪影、部分容积伪影等），高斯滤波函数效果一般，很难去处伪影的影响；本文采用Gabor滤波+Gaussian滤波的方式，以求在保证图像边缘的同时，去除伪影和噪声的影响。

Gabor滤波器具有在空间域和频率域同时取得局部最优的特性，因此能够很好地描述空间频率（尺度）、空间位置及方向选择性等局部结构信息。Gabor滤波器的频率和方向表示接近人类视觉系统，常用于纹理表示和描述。二维Gabor小波变换是图像的多尺度表示和分析的良好工具[7-8]。

二维Gabor滤波函数φ(x,y)如公式(6)所示：

其中，σx和σy分别为X轴和Y轴上的标准方差，决定了滤波器作用区域的大小；ωx为复正弦函数在横轴上的频率。

图像的Gabor滤波可通过图像I(x,y)与Gabor函数φ(x,y)的卷积来完成。将(6)式的Gabor滤波器函数分解成为实部φR(x,y)和虚部φI(x,y)两个分量，则其作用于图像I(x,y)进行滤波如公式(7)所示：

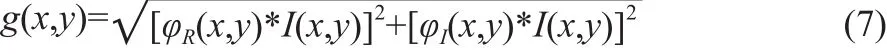
其中，*代表卷积运算；g(x,y)为Gabor滤波器提取出的特征图像[9]。

2.2 对双阈值检测连接边缘的改进

传统的Canny算子进行双阈值检测连接边缘时，对整幅图像采用了两个阈值T1和T2，一般取T2=2×T1，得阈值边缘图N1(x,y)和阈值图像N2(x,y)。后者通过使用高阈值得到，因此没有假边缘，但是中间会有不连续的地方。在N2(x,y)中对边缘进行连接，形成轮廓，结束的时候，就在N1(x,y)的8邻域位置寻找合适匹配的边缘，反复地进行，在N1(x,y)中循环收集图像边缘，直到N2(x,y)连接好为止。所以，两个阈值的选取对最终得到的边缘有决定作用。传统的阈值选取往往是通过经验或者是随机选择，不能适用于每幅脑部MR图像的检测，得到的边缘往往误差较大[10-11]。

本文对其进行改进，在双阈值检测时，采用Ostu算法，主要思想为：按图像的灰度特性,将图像分成背景和目标两部分。背景和目标之间的类间方差越大，说明构成图像的两部分的差别越大，当部分目标错分为背景或部分背景错分为目标都会导致两部分差别变小，这使得类间方差最大的分割错分概率最小[12-13]。

本文算法基于Ostu的思想，设使用阈值T将图像分为目标和背景两部分，即：目标C0=[0,T-1]；背景C1=[T,255]。则目标C0和背景C1产生的概率分别为：

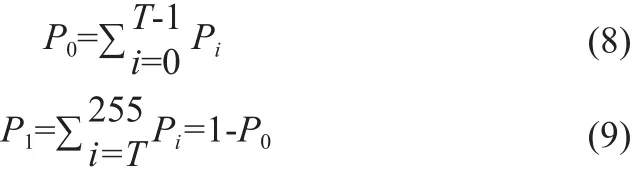
所以目标和背景部分所对应的平均灰度分别为：

整幅图像的平均灰度为：

目标和背景区域的总方差则为：

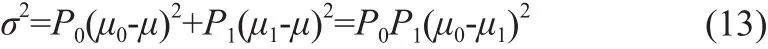
故在确定双阈值时，使得T在[0，255]区间范围内由小到大变化，取使得σ2最大的T作为高阈值T2，取低阈值T1=T2/2。

3 实验结果与分析

3.1 实验对比

本文分别以Shepp-Logan数字体模和实际采集到的脑部MR图像为实验对象，如图3a以及图4a所示，对传统的Canny算子以及本文所提出的改进Canny算子分别采用Visual Studio 2010 + Open CV平台编程实现[14-16]，对比验证本文所提出的改进算法的有效性。图3b以及图4b为传统Canny算子分割结果，图3c和图4c为本文提出的改进Canny算子分割的结果。

3.2 结果分析

由图3对比可看出，对于Shepp-Logan数字体模，没有噪声干扰，改进后的Canny算子可以提取到精确的图像轮廓，而传统Canny算子轮廓提取效果会受到高低阈值的影响，图3b是高低阈值分别为80，160的检测结果。由于阈值不能提前获知，只能通过先验知识设置或逐步更改阈值进行测试。图5显示了不同阈值下的检测结果。

而改进后的Canny算子不需手动设置高低阈值，可自动计算出最优分割时的阈值，减少了人工干预，增加了分割的精细度。

图3 Shepp体模检测对比

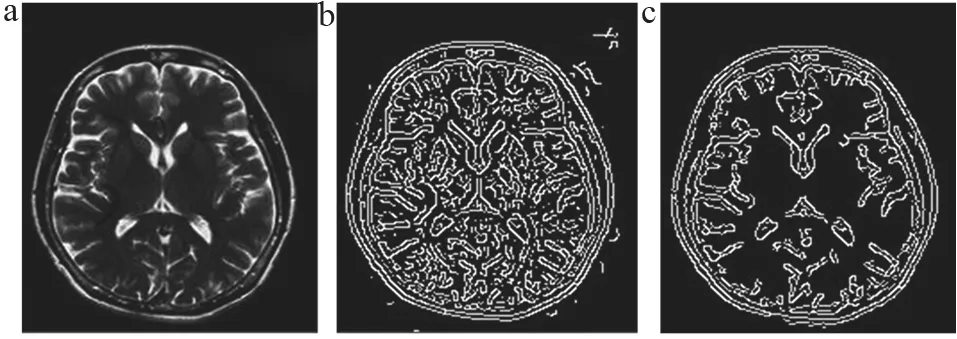
图4 脑部MR图像检测对比

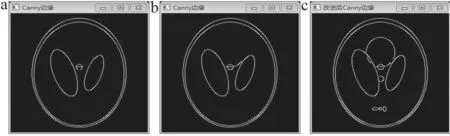
图5 不同高低阈值下传统Canny算子检测结果

由图4对比可看到，在实际采集到的脑部MR图像中，由于受到噪声以及伪影等的干扰，传统Canny算子检测到的轮廓会产生伪边缘（图4b）；而改进后的Canny算子加入了Gabor滤波，尽可能去除了伪影等噪声的影响，具有更高的鲁棒性（图4c）。

4 结语

针对传统的Canny算子存在的易受噪声干扰以及最终结果受高低阈值设置影响等缺陷，本文提出改进的Canny算子，加入Gabor滤波，并结合Ostu自动阈值计算。实验对比结果表明，改进后的Canny算子在医学图像领域尤其是脑部MR图像方面取得了更好的发展与应用，使得图像处理技术为临床诊断提供了极为重要的临床意义。