一种基于最小二乘法的离散点螺旋线式拟合算法

尤中桐 王太勇 刘清建 辛全琦

1.天津大学机械工程学院，天津，300350

2.天津职业大学机械工程与自动化学院，天津，300410

0 引言

在对非圆二次曲线与样条曲线轮廓进行机械加工时，一般做法是在特定的容差范围内用一系列折线替代原始曲线［1］，或用圆弧、双圆弧逼近原始曲线［2⁃3］。但是这种方法存在拟合精度不够高或程序段多等缺点，造成机床频繁加减速，进而影响到实际的加工精度与效率。所以探索一种既能保证较高精度，又能减少数据量的曲线离散点拟合算法显得十分重要。一些学者采用阿基米德螺线拟合曲线离散点，进行了数控加工的研究工作。王可等［4］在分析了阿基米德螺线特性与误差计算方法后，用阿基米德螺线逼近涡旋盘轮廓，并将其与直线、圆弧拟合对比，指出阿基米德螺线的逼近特性优于直线和圆弧。张彦博［5］提出了一种用阿基米德螺线逼近椭圆来获得曲线节点的算法，并通过一个实例证明，在精度满足要求的前提下，该算法比等误差直线逼近的程序段少得多。他们在求解阿基米德螺线参数时只用到了首末两点，没有兼顾到中间点对参数计算的影响。李泽蓉等［6］用平面二维优化方法求解阿基米德螺线参数来逼近大直径圆弧，但是其计算涉及迭代，较为复杂，计算量也较大。

本文分析了阿基米德螺线上某一点处切矢、径矢夹角与螺线参数的关系，为近似确定阿基米德螺线段的中心提供依据。拟合算法基于最小二乘原理，把中间数据点的误差平方和作为目标函数，引入约束条件，考虑了中间数据点对阿基米德螺线参数计算的影响。通过对离散点集进行前寻、回溯，在保证精度的前提下，用阿基米德螺线与小线段完成离散点集的拟合。最后通过一个实例验证所提算法，并将其与文献［4⁃5］的方法和文献［2］的圆弧拟合方法相对比，证明本文方法的优势与应用价值。

1 基于不完全约束最小二乘原理的拟合算法

1.1 阿基米德螺线方程

如图1所示，阿基米德螺线的极坐标方程可表示为

式中，ρ为螺线上的P点到螺线中心O的距离；θ为射线OP与X轴正方向的夹角；ρ0、v0为常数，ρ0为零度角对应的螺旋线上的点到螺线中心的距离；v0为单位角度变化量对应的距离增量。

图1 平面阿基米德螺线Fig.1 Archimedes spiral in the plane

由式（1）可得到对应的直角坐标参数方程：

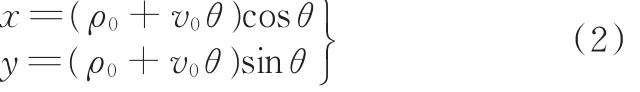
1.2 阿基米德螺线中心坐标的确定

如图1所示，假设P点处螺线切矢T=（Tx，Ty），径矢R=（Rx，Ry），二者的夹角为α，则有

依次取 θ=0o，60o，120o；以|ρ0/v0|为自变量研究其与夹角α的关系，在MATLAB中绘制二者的关系曲线，如图2所示。

图2 |ρ0/v0|与α的关系Fig.2 The relationship between|ρ0/v0|and α

就拟合计算得到的阿基米德螺线而言，|ρ0/v0|一般大于50，由图2可知此时α接近90°，即T与R两向量近似垂直。所以在确定螺线中心时，可以把阿基米德螺线当作圆弧处理，将首末两端点的法线交点作为螺线中心。如图3所示，实际计算时，以通过该段首点且垂直于首点与第二个点连线的直线为该段首点处的法线，同理，可确定该段尾点的法线。联立两直线方程，即可求得该段螺线中心点O的坐标。

图3 计算螺线中心点坐标Fig.3 Calculation of center point of the spiral

1.3 ρ0与v0的求解

就一段阿基米德螺线的方程而言，其未知参数为ρ0、v0、中心坐标（x0，y0），上文已经确定了中心坐标，所以还剩ρ0、v0待求解。前人往往仅利用首末两点构建方程组来求解ρ0与v0，忽视了中间点的影响。本文采用不完全约束最小二乘法来保证拟合精度，同时妥善处理拟合后曲线连续性的问题，考虑中间数据点对参数计算的影响，以较少段螺线拟合所有数据点。不完全约束最小二乘法是指，拟合计算后曲线的起点与终点是原有数据点列的起点与终点，螺线段之间的连接节点不一定是原数据点列中的点。如图4所示，对以一段螺线拟合的数据点列而言，螺线终点一般并不与该数据点列的最后一个点重合。把该数据点列最后一个点对应的角度代入拟合计算出的螺线方程，可以得到螺线终点，用得到的螺线终点替代该数据点列的最后一个点，同时作为下一段螺线的起点，如图4中的连接节点G。

图4 不完全约束最小二乘螺线拟合Fig.4 Spiral fitting based on incomplete constraint least square method

假设某段螺线要拟合的数据点为P1(ρ1,θ1)，P2(ρ2,θ2)，…，Pn(ρn,θn)。构造目标函数S：

其中，ρi为点 Pi到螺线中心的距离，θi为点 Pi与螺线中心的连线同X轴正方向的夹角，二者均可通过点Pi的直角坐标求得。

引入螺线通过首点这一约束条件：

这样对参数ρ0与v0的求解就转化为约束条件下的优化问题。根据拉格朗日乘子法［7］，定义新函数

这样关于参数ρ0与v0的约束条件下的优化问题就转化成了关于F的无约束优化问题，确定F(ρ0,v0,k)的极值时，可利用其偏导数为零进行求解：

化简式（8）得到线性方程组：

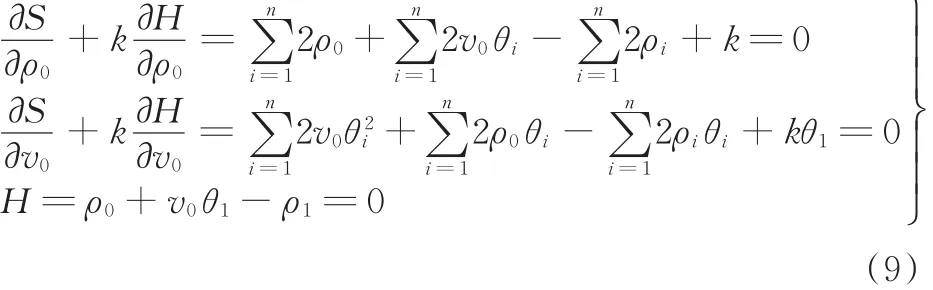
即可求解ρ0与 v0。

1.4 拟合误差的计算

在图5中，根据点集{ps,ps+1,ps+2,…,pi，…，pe-2,pe-1,pe}，利用前述计算方法得到的螺线方程ρ = ρ0+v0θ，中心点为 O′。除首点 ps外，点集中某点Pi的拟合误差δpi的计算可采用以下方法：①计算点Pi在坐标系X′O′Y′中的坐标，进而得到其对应的极径ρp与转角α；②把α代入螺线方程，得到点对应的极径；③pi与两点极径差值的绝对值即为点pi处的拟合误差。即

图5 拟合误差计算Fig.5 The calculation of the fitting error

设ε为该段螺线的拟合误差，则

1.5 数据点的前寻与回溯

对于离散点的拟合计算，由于无法预知其转折点、尖点等特征信息，所以在拟合计算过程中，最好能遍历所有数据点，以保证不会丢失某些关键数据点，从而不丧失原轮廓的特征信息。本文采用了一种前寻、回溯方法［8］来搜寻、遍历所有数据点。如图6所示，若点集的当前尾点为pi且拟合误差满足要求时，则向前搜寻点pi+1作为新的尾点，重新进行拟合计算，判断是否满足误差条件，这称为数据点前寻；若点集的当前尾点为pi且拟合误差不满足要求，则向后搜寻点pi⁃1作为新尾点，这时的点集即为某段待拟合的点集，这称为数据点回溯。该前寻、回溯方法最大限度地拟合一段螺线较多的数据点。

图6 前寻回溯数据点Fig.6 Search forward and backward the data points

1.6 拟合算法的流程

拟合算法流程见图7，具体步骤如下：

（1）输入待拟合的离散点集。

（2）读入第一个数据点，将其作为首点。

（3）判断待读取数据点的个数：若为0，则结束拟合算法；若为1，则输出首点与待读取的最后一个点确定的小线段，结束拟合算法；若大于等于2，则读入2个数据点，开始拟合计算。

（4）判断该段拟合的首点与步骤（3）读取的两点是否共线：若共线，则输出第一点与第三点确定的小线段，同时把第三点作为下段拟合的首点，转到步骤（3）；若不共线，则根据上文的计算方法用这三点计算螺线参数，然后计算拟合误差ε。

（5）判断拟合误差ε是否满足要求：若满足要求，则转到步骤（7）；若不满足要求，则转到步骤（6）。

（6）如果拟合的数据点数超过3，则回溯一个数据点，根据这时的数据点集计算螺线参数并输出，同时根据这组参数更新尾点坐标，作为下段拟合的首点；如果拟合的数据点数是3，则输出前2个点确定的小线段，同时尾点回溯一个数据点，作为下段拟合的首点。转到步骤（3）。

（7）判断是否还有数据点待读取：若有，则前寻一个数据点，然后根据这时的数据点集重新计算螺线参数与拟合误差ε，转到步骤（5）；若没有，则输出上次计算出的螺线参数，结束拟合算法。

图7 拟合算法流程图Fig.7 The flow chart of fitting algorithm

2 算法仿真与分析

上述算法已经通过Visual C++编程实现，现以一含有255个数据点的点集为例，在计算机上进行该算法的仿真测试分析。测试环境如下：操作系统为Windows 7旗舰版；内存为8 GB；CPU为Inter Core i5⁃4570 3.20 GHz。

给定拟合精度5 μm，采用本文算法计算得到所需阿基米德螺线段数为27，如图8所示，实心点为离散点，空心点为螺线端点，实线为螺线，表明这些螺线段很好地拟合了离散点。

图8 基于最小二乘法的阿基米德螺线拟合结果Fig.8 Spiral fitting result based on least square method

给定拟合精度5 μm，采用文献［2］的圆弧拟合算法去拟合这些数据点，计算得到所需圆弧段数为56，如图9所示。

图9 基于文献［2］最小二乘法的圆弧拟合结果Fig.9 Circle fitting result based on the least square method from reference［2］

给定拟合精度5 μm，采用文献［4⁃5］中仅用首末两点的方法计算得到所需螺线段数为31，如图10所示，比本文拟合算法多出4段螺线，且增加的4段螺线均出现在曲率变化剧烈的部分，可见本文提出的算法要优于文献［4⁃5］方法。对比以上3种结果可知，相同拟合精度下，基于最小二乘法的阿基米德螺线拟合算法能使数据量得到缩减。

使用53段阿基米德螺线，分别采用本文提出的算法与文献［4⁃5］的方法去拟合该离散点集，再使用53段圆弧采用文献［2］的方法去拟合该离散点集，得到各自的拟合误差如图11～图13所示。段数相同时，基于最小二乘法的阿基米德螺线拟合算法的精度更高，再将其与已有的阿基米德螺线插补算法［9⁃10］结合，便可实现离散点集基于离散点螺旋线式拟合算法的数控加工。

图10 基于文献［4-5］方法的阿基米德螺线拟合结果Fig.10 Spiral fitting result based on the method from reference［4-5］

图11 基于最小二乘法的阿基米德螺线拟合误差Fig.11 Sspiral fitting error based on the least square method

图12 基于文献［4-5］方法的阿基米德螺线拟合误差Fig.12 Spiral fitting error based on the method from reference［4-5］

图13 基于文献［2］最小二乘法的圆弧拟合误差Fig.13 Circle fitting error based on the least square method from reference［2］

为了比较本文所提算法与前人算法的时间花费，在给定相同的数据点集（上述255个数据点）与拟合精度（10 μm、5 μm、1 μm）的前提下，通过调用Windows系统的API高精度计时函数Query⁃PerformanceCounter（）可得到3种算法的运行时间，如表1所示。可知本文提出的拟合算法在计算效率上介于文献［4⁃5］的拟合算法与文献［2］的拟合算法之间。

表1 三种算法的运行时间Tab.1 The running time of the three algorithms

3 结论

（1）阿基米德螺线上某点处的切矢、径矢夹角随 |ρ0/v0|的增大而趋近于90°。

（2）通过最小二乘法引入了中间数据点对螺线参数计算的影响。与前人算法相比，本文算法具有更好的数据压缩效果。

（3）在相同段数的前提下，使用基于最小二乘法的阿基米德螺线拟合离散点集，具有更高的拟合精度。