浅谈高中数学教学中数学文化的渗透

欧阳建胜

(福建省泉州实验中学 362000)

一、数学文化在几何体外接球教学中的渗透

立体几何对一般学生来说，由于缺乏一定的空间想象能力和抽象能力，学生学起来还是比较吃力的，久而久之，会让学生的学习激情大大降低，适当地结合数学文化教学，能加深印象，提高学习效率.

案例1 探究几何体外接球的球心.

立几外接球的表面积或是体积的求解，是立几题型的要点之一，也是很多同学感觉比较困难的题型之一，而要解决这类问题，很关键的一个步骤是确定球心的位置.由于立几图形的抽象性，很多同学都找不到点上，所以对这种问题都比较为难.下面，我们来探究下几类可以转化为长方体外接球的几何体的外接球球心.

请在图中作出下列几何体的外接球球心.(1)长方体ABCD-A′B′C′D′.(2)直棱柱ABC-A′B′C′，其中∠ACB=90°(古文称之为壍堵).

(3)已知四棱锥P-ABCD中，PA⊥平面ABCD，其中ABCD为矩形(古文称之为阳马).

(4)已知三棱锥P-ABC中，PA⊥平面ABC，其中∠ACB=90°(古文称之为鳖臑).

(5)已知三棱锥P-ABD中，PA⊥平面ABD，其中∠DAB=90°(古文称之为墙角).

(6)已知三棱锥P-ABC中，PA=BC,PC=AB,PB=AC.

方法：利用长方体为载体，通过补形，可把这几类几何体的外接球转化为长方体的外接球.

在教学过程中渗透数学文化知识，尤其是这几个古文名称，很不好读，当场查询，多读几遍，让学生有更深刻的印象，为熟练掌握这几类几何体求外接球等相关问题提供了很好的帮助.

二、数学文化在三角形面积求解教学中的渗透

三角形面积的求解，在正余弦定理这个章节上显得特别重要，也是高考考查的内容之一，近年来的高考题型中经常出现这个考点.如何结合正余弦定理这个章节的内容，利用三角形最基本的元素来求解，显然是这个考点的重要内容.那么在推导出新的面积求解公式后，我们不妨进一步探究一下不同类型的求解方法.

案例2 探求三边长的三角形面积.

在△ABC中，已知三边a,b,c的长度，求△ABC的面积.

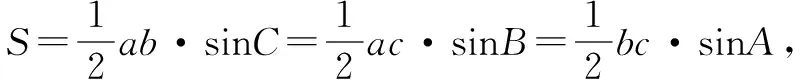
三、数学文化在数列递推关系教学中的渗透

数列内容中的递推关系是整章的重难点内容，它的逻辑推理能力要求较高，很多同学刚开始接触，一脸茫然，不知从何下手，甚至产生了放弃的想法.如果能在教学过程中渗透一些数学文化，引导学生观察数据的变化规律，让学生发现数学的美，可以培养学生的学习兴趣！

案例3 利用杨辉三角数的规律探究递推关系

观察杨辉三角：

思考1 杨辉三角中数字的排放顺序是有规律性的，并且是比较直观的.(比较容易观察，可以让学生畅所欲言，容易引发学生的探究欲望.)那么你能观察出哪些规律呢？

基于对数字上下、左右结构的特点，学生加以分析，教师适当的引导，容易得出对称性和总和性，亦即两个常见的组合数公式.有了前面成功的基础，那接下来，下面的研究就可以继续地进行了.

思考2 如果我们换个角度看待这些数，比如看下图斜线，每条线上的数相加又有什么规律？如果从数列的角度来观察这些和，又能得出什么不一样的结论？

慢慢地从学生的角度，引导学生去观察和思考，从而培养学生的探索能力，有助于发展他们思维的深度和广度，而这也恰恰是学生所缺漏的.在此题中，我们不难得出以下数据：1，1，2，3，5，8，13，21，34，…

记此数列为{an},则有a1=a2=1,an+2=an+an+1.这个数列从第三项开始，每一项是它前面两项的和，这个数列，我们把它称为斐波那契数列.接下来，我们可以适当地介绍下这个数列的发展史，斐波那契是意大利数学家，在他的著作《算盘全书》中以兔子繁殖为背景，提出了这个问题.这个数列如果继续研究下去，还可以得出很多有趣的结论，这样，学生对这个数列的认识就会更加深刻，为递推数列的推理取得了一定的效果，甚至还可以扩充学生的思维，原来事物的联系是如此的巧妙，现实生活中隐藏着很多特别有趣的数学文化，中西文化也可以这样完美地融合在一起.接着，我们可以继续来研究以下这个问题.

思考3 前阶段有个号称要打败淘宝的“云联惠”电商平台，它的运营模式是“买多少，返多少”，号称全部让利给客户，它的返还金是递减式的.比如你买了10000元钱，云联惠会以每天万分之五的递减式返还给您，直至返还完.那么请问同学们，要用多久才能把这10000元钱返还完？首先，要解决这个问题，那么我们就要真正去弄清楚它的这个返还模式;我们如果消费10000元，第一天按万分之五返还，那么第一天就是返还5元，但是第二天呢？还是5元吗？错了，第二天返还的是剩下9995元的万分之五，第三天返还的是扣除前两天返还剩下的万分之五，依此类推……所以，每天返还的钱数是越来越少.从数列的角度分析，这也是个递推数列的问题，我们把每天返还的钱数看作数列的每一项，那你们能写出这个数列的递推公式吗？显然a1=5,a2=(10000-a1)×0.0005,……,an=[10000-(a1+a2+…+an-1)]×0.0005，利用数列求和，10000元要全部返还的话至少要100年.显然，这是一个多么精致的骗局，不懂内幕的消费者，以为一天返还5元，2000天也就是5年多就能再多赚10000元，何乐而不为.而且据说那平台里面的产品比其他地方的贵，它就是打着“消费全返”的旗号在骗取用户的消费，而且它对进驻的商家也有类似的做法.这再次说明了数学的重要性，没有一定的数学文化，可能我们很容易就会上当受骗.

总之，在平时的数学教学中，适当地渗透数学文化，既可以丰富整节课的内容，又可以调节课堂氛围，还可以培养学生对学习数学的兴趣，更可以传承古代数学的美与思想，真的值得我们去尝试.当然，我们自身也要加强对数学文化的了解，以及研究如何合理地在教学中渗透数学文化，才能取得最佳的效果.也许就是因为你的传承，下一个数学家将在你的座下诞生！