基于特征组合段理论研究数控铣削加工参数优化—以洗衣机金属波轮零件为例

张 磊

淮北职业技术学院机电工程系，淮北，235000

洗衣机的波轮部件，由众多复杂非规则曲面构成，要求加工精度高，表面粗糙度值小，属于难加工零件。类似研究较多的是自适应在线数控铣削参数优化［1］，原理是利用数控铣床的CNC和测试系统，监控加工中动态切削力，满足约束条件下，数控铣床CNC系统能够自动调解主轴转速和背吃刀量，得到期望的加工参数，但有时传感器等器件稳定性及成本难如人愿，一定程度上会影响其实际应用。也有采用离线参数优化方法研究波轮加工参数，即基于经验，预指定各工序参数，以零件成本、效率和质量的一个或多个作为参数，建立目标函数模型，用合适优化算法为某加工工序选择一组固定的最佳参数，而后用数控仿真验证确认。因实际生产的复杂性，这种优化参数方法在应用上存在一定的局限性，比如优化目标函数效率高，能够优化出最短加工时间和最快加工速度的参数，但这并不意味着加工效率就最高，因质量和成本等参数对效率也影响巨大，故应是多目标的优化参数［2］。

实际加工波轮零件时，时间、速度、成本、质量等参数相互制约，不同工序的优化目标也应不同。基于此，本文针对洗衣机波轮零件探讨多目标加工参数优化问题。但考虑到其加工的每次走刀中，既包含切削速度、切削深度、切削宽度和每齿进给量优化加工参数信息，也势必会产生切削力、加工误差目标约束信息，如果将包含加工参数信息和约束信息的走刀定义为加工特征段，那么自动生成的数控加工程序就可能包含上万个加工特征段，若每个加工特征段都进行参数优化，不仅计算时间长，而且需要随时调整机床参数，这在加工过程中不可能做到。

基于此，本文在文献［1-3］基础上，提出了用加工特征组合段理论研究洗衣机波轮加工多目标参数优化问题，并用优化参数和经验参数通过NC程序对其铣削时间和成本进行验证，求解算法正确有效。

1 构建波轮零件数控铣削加工参数优化数学模型

1.1 加工特征段

数控铣削工艺过程包括工序、工步和走刀，每一个走刀中的特征可以用切削速度、切削深度、切削宽度和每齿进给量参数进行描述，构成走刀中的几何信息。走刀中的物理信息可以用铣削力和加工误差进行描述，将既包含几何信息和物理信息的走刀定义为加工特征段［2］。

1.2 设计变量

实际波轮零件铣削中为了取得较好的优化效果，应对每一个加工特征段都进行优化，但存在NC计算处理时间长、需要时刻调整加工参数的弊端。实际上每个特征段的切削深度和切削宽度大致相当，为此将各个加工段组合起来一并进行参数优化，这就大大降低了控制的复杂性。整个零件的加工过程可以用设计矢量X表示成（1）式，可以视为n个加工程序段构成。

式中，Fzi为铣刀的每齿进给量；vi为对应于切削深度api、切削宽度aei下的切削速度。

1.3 目标函数

目标函数是加工时间、生产成本和产品质量［4］。

（1）加工时间

如果用相同参数，使用单一刀具加工完一个零件所需时间包括加工时间、换刀时间和辅助时间，用式（2）定义。

式中，tm为铣削时间；f为进给率；L为铣削长度；tc为更换一次铣刀所用时间；tt为铣刀平均寿命；tz为工装设备准备时间；v为铣削速度；fz为铣刀每齿进给量；z为铣刀齿数；D为工件直径；cv、qv、kv、m、yv、xv、uv、pv为常数系数，可以查金属切削手册得到。如果使用不同的设计参数，一个波轮零件总加工用式（3）表示。

（2）加工成本

用式（4）定义一个单独波轮零件使用相同工艺参数的加工成本。

式中c1为铣刀消耗成本；ct为单位时间劳动力消耗成本及其他各类生产性支出成本。

当使用不同参数，一个完整加工过程总成本用式（5）表示。

数控铣床的参数优化是一个非线性规划问题，涉及机床、刀具、夹具和工艺等属性［5］。为追求加工时间和加工成本的最佳组合，本文采用多目标线性加权求和法建立（6）式数学模型，作为多目标函数评判标准，用于通过参数优化达到数控机床工装最佳使用。

式中，Tallo、Cpo分别为优化前的加工时间、加工成本，λ1、λ2分别为反映加工成本和时间重要程度的权重系数，一般根据经验选定。为克服不同量纲的影响，将（3）（5）代入（6）将单一目标函数归集成综合目标函数。

1.4 约束条件

1.4.1 平均切削力的约束

式中，Pxp为与工件材料和刀具相关的系数，MR（v，fz，ae，ap）为材料切除率，与刀具每齿进给量、切削深度、切削宽度以及进给速度有关。Fmax为机床许用最大进给力，ρ是切削进给力与平均切向进给力比值。

1.4.2 瞬时切削力的约束

即瞬时法向切削力Fn应不大于机床最大许用切削力 Fmax，N。

1.4.3 基于材料切除率功率约束

式中，Pmax为机床输出功率的最大值，η为功率的系数。

1.4.4 主轴转速约束

式中，nmax和nmin为机床允许最大最小转速。

式中，fmax和fmin为机床允许最大最小进给速度。

1.4.6 加工误差约束

式中，δ和δmin为工件表面加工误差及最大允许加工误差。

1.4.5 进给速度约束

1.5 加工参数优化模型

基于上述设计变量、约束条件和优化目标，构建优化模型。

2 加工参数优化

式（13）的优化模型中，设计参数 vi（i＝1，2，…，n）、fni（i＝1，2，…，n）共有 2n个，过多参数不利于求解，为此先利用数控仿真软件获得每次走刀的切削深度和切削宽度，找出最大最小的切削深度和切削宽度区间，并分成3个等宽子区间，所有走刀的切削深度和宽度都会落入上述3个子区间内，统计出落入3个不同子区间的走刀次数和子区间的平均切削深度、切削宽度，这样在同一子区间的所有走刀都用平均切削深度和切削宽度表示，构成了加工特征组合段，优化问题的求解难度会大大降低［2］。

2.1 优化问题分解

不同的加工特征组合段具有不同的设计参数，即各个加工特征组合段的每齿进给量fZ和切削速度v之间相互独立，所以将综合目标函数分解成子目标函数之和，如式（14）所示。

式中 Mi（vi，fzi）是子目标函数，C是固定的加工准备工时所对应的成本归一化处理后的值。

由于各个加工特征组合段的切削条件相互独立，所以可以将式（14）综合目标函数优化转化成式（15）的n个子目标函数优化问题，进而通过对各加工特征组合段的局部优化达到全局优化之目的。

2.2 遗传算法优化

式（16）描述的是加工波轮零件的第i个特征组合段目标函数，是带约束的最小优化数学模型，如果使用传统的优化方法对其优化，计算麻烦，也很难能搜寻到全局最优解［3］，如果将此转化为带罚函数的无约束优化数学模型并进行优化计算，问题可得到简化。

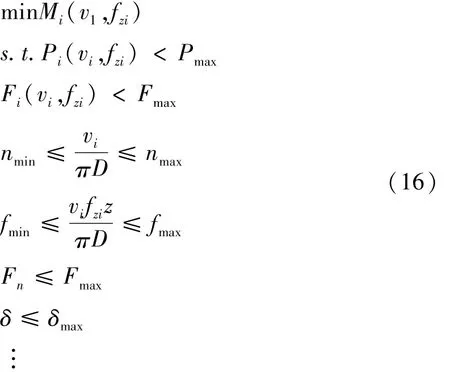
取适应度函数S为优化目标函数，则第i个加工特征段相应的适应度函数Si为式（17）。式中惩罚项是 RjP（x），惩罚因子是 Pj（x）＝Rj［min（0，x）］2；Rj（j＝1，2，…，6）

遗传优化算法的步骤［6］为：

（1）编码。对每一个设计参数根据需要按不同长度进行二进制编码，构成一个整体染色体串。

设任意参数 xi的上下线是 ximax、ximin，xi用长度是k的二进制编码表示，设为mi，则用式（18）表示xi和mi之间的关系。

（2）选择。赌轮选择法，即适应度越高的个体被选择的概率就越大。

（3）交叉。先采用单点交叉法，如果连续几代参数都未被选中，为了提高搜索效果，可以采用两点交叉加速收敛。

（4）变异。对待操作的个体任选其一进行取反操作，即一点变异法。

（5）群体规模PS的设定。PS过大，收敛极慢，PS太小，又难以收敛到实际值。

（6）遗传算法初始参数设定。初始种群为PS＝100，变异概率为 Pm＝0.01，交叉概率为 Pc＝0.95，迭代次数为Imax＝2000。

（7）染色体种群的初始化。评判标准取式（17）中Rj＝1000，染色体种群随机取100个种群，并在v、fz的区域中，即 fzmin≤fz≤fzmax、vmin≤v≤vmax。

3 波轮零件的优化验证

3.1 实验参数

波轮零件毛坯材料为Ly12，根据其技术要求，在数控铣床上需要经过粗铣、半精铣和精铣三道工序才能完成，各道工序的铣削参数如表1所示。

表1 波轮零件的数控铣削参数

3.2 参数的优化过程

在计算机上用数控仿真软件，对波轮零件分别进行粗铣、半精铣、精铣，获得铣削宽度、铣削深度与走刀次数的关系，构造加工特征组合段共计12个，其中粗铣5个，半精铣5个，精铣2个，具体划分如表2。仿真优化计算选取的通用参数和加工参数见表2和表3。

表2 波轮零件数控铣特征组合段划分表

表3 通用参数表

利用上述遗传算法对波轮零件加工特征组合段的切削速度和每齿进给量进行优化，经验参数和优化参数见表4。

表4 优化参数和经验参数对比表

3.3 优化结果验证

用经验参数和优化后参数进行铣削波轮零件，分别测定其所需要时间和成本，对比结果见表5。

由此可见，参数优化后加工时间减少了15.61%，加工费用降低了14.12%，优化后的参数经过验证效果明显。

表5 优化前后比较结果

4 结论

针对洗衣机波轮零件数控铣削参数优化问题，引入加工特征段概念，利用数控加工仿真软件，计算出每次走刀的切削深度、宽度并划分成不同区间，在每个组合划分区间内所有走刀次数构成一个加工特征组合段上构建多目标优化模型，模型用遗传算法对每个数控铣削加工特征组合段进行参数优化，并用优化参数和经验参数通过NC程序验证其铣削时间和成本，在保证零件质量前提下，降低了成本，缩短了加工时间，说明模型建立和算法的可行性。