基于SM算法的钢桁架结构冗余度优化

吴星煌， 朱南海

（江西理工大学建筑与测绘工程学院，江西 赣州341000）

钢桁架桥梁以其结构造型优美、受力合理、跨越性好受到广泛关注[1].鉴于材料成本、拼接工艺、拓扑构型等因素，设计一个受力合理、用量少、成本低的结构成了一个亟待解决的优化问题.以往在截面设计方面多是按极限状态设计方法进行，通过逐个考虑构件的承载能力和节点的位移来获得构件的截面尺寸，该方法并没能考虑到结构的整体效应，不能形成合理的受力模式而有效发挥构件的性能.所以亟待找到一种能够反映结构整体性能的量，并运用优化算法来对该量进行解的搜索方法.

结构冗余度作为反映结构在局部危险状态下保证构件受力替补性和内力重分布的一个量[2]，恰好可以用来反应结构的整体性能.文献[3-4]基于结构刚度给出了结构冗余度的计算方法，却没有考虑荷载对结构冗余度的影响；文献[5]讨论了荷载对结构冗余度的影响；文献[6]基于敏感性理论分析了荷载作用下结构冗余度.所以需要一个能考虑荷载作用、结构几何属性的冗余度评估方法，并能有一个高效的算法对冗余度进行优化从而实现结构的优化设计.在结构的优化设计上主要有截面优化、形状优化、拓扑优化和选型优化[7].截面优化作为结构优化设计最基础的一步，通常伴随着单纯形算法、模拟退火算法、遗传算法等运用,文献[8-11]分别对这几种优化算法及其混合算法在截面优化设计上的运用做了相应的研究，鉴于对算法搜索效率的考虑，选取SM算法(单纯形算法)做结构冗余度优化来实现构件截面的优化设计.

SM算法作为一种简单、局部搜索效率高的确定性下降的方法,通过引入结构冗余度的概念并做相应改进后完全可以适用钢桁架桥的截面设计.文中将传统无条件约束的局部搜索能力的SM算法做了一个改进，首先将解的搜索空间扩大了一倍，其次对解的边界进行自适应处理，然后在每代新解中引入变异[12]，最后运用理想点法[13]将结构冗余度差值最小、结构体积最小两个目标整合成一个目标函数后形成一个具备全局搜索能力的改进SM算法.通过改进SM算法对符合目标函数的解空间的搜索，选出了钢桁架桥构件最优截面，最后以Abaqus仿真分析的结果来验证算法在钢桁架桥截面优化设计中的有效性.

1 结构冗余度计算

结构冗余度与结构响应敏感性成反比，根据Pandey等[14]基于敏感性理论在冗余度上的研究，提出如下冗余度评价指标：

式（1）中：GRi为构件单元i的冗余度；NE为结构单元总数；Vj为j单元的体积；Sji为j单元对第i单元的应变响应敏感性；V为结构总体积.

2 SM算法改进及其对冗余度的优化

2.1 传统SM算法理论

传统SM算法是一种从n+1个顶点出发，不断重复反射、延伸、缩短、缩边过程直到满足目标终止条件的多面体搜索算法，是一种局部搜索速度快、无条件约束的确定性算法，主要由以下几部分组成：

1）n+1个初始解的产生

式 （4） 中：X0为初始解矩阵；n为变量的维数；fieldDR为描述变量上下边界的矩阵；crtrp为遗传算法中产生符合均匀分布实值的函数，详情参阅文献[17].

2）解的反射

式（5）中：X0,r为反射的解矩阵；Xh0为最大目标函数值的解；X0,mean为除去Xh0后X0中所剩解的均值；reflct为以X0,mean为反射中心的反射系数.3）解的延伸

式（6）中：X0,e为延伸的解矩阵；extd为延伸系数.

4）解的缩短

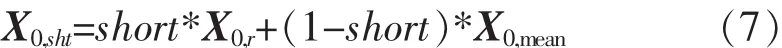
式（7）中：X0,sht为缩短的解向量；short为缩短系数.

5）解的缩边

式（8）中：Xi0为解空间 X0中第 i个解向量；Xl0为最小目标函数值的解；shrnk为缩边系数.

6）终止条件

式（9）中：fT0为终目标函数；fl0为最小目标函数；eTol为判敛误差限；sqrt、sum分别为开方、求和函数.

2.2 传统SM算法改进

为适应结构冗余度优化对搜索速度和数据精度的要求，并获得一个在有边界约束条件下具备全局搜索能力的SM算法，现对SM算法做如下改进：

改进1，借鉴复形法[18]，将初始搜索顶点由n+1扩展成2n，防止多面体搜索空间退化.

改进2，对边界约束做如下自适应处理：

式（10）中：x0,i为解 X0第 i个分量为 x0，i下限；xu0为 x0，i上限；mod为取余数函数.

改进3，为增强算法的全局搜索能力，在每次搜索循环后对新解产生一个符合柯西分布[19]的随机扰动后再进入新一轮的搜索，具体如下：

式（11）、式（12）中：deltax 为柯西随机扰动；xl0,i为扰动后产生的新解；x0l为上一轮搜索的优化解；Cauchyrnd为柯西分布随机函数；其中α取0，θ取1.

改进4，为防止过度优化和循环次数过多，将式（9）改为：

式 （13） 中：log fT0、log fl0分别为 fT0、fl0取自然对数的值，保证优化前后的解在同一量级时就终止.

2.3 改进SM算法对结构冗余度的优化

结构冗余度初始优化模型为：

式（14）中：f0、f0V分别为结构冗余度、结构体积的目标函数；XL0、XU0分别为解空间的下、上限向量.

为使改进后的SM算法能一次性考虑结构冗余度优化中的两个目标，对式（14）用理想点法将结构冗余度最小、结构体积最小两个目标进行多目标优化[20]整合，得最终结构冗余度优化模型为：

式（15）中：min fT0为终目标函数最小值；fT为目标函数f0、f0V的解空间；min V为最小体积值；T为理想点空间；min T为理想点空间集；repmat为矩阵复制函数，用来得到2n个理想点空间.

结合式（4）～式（13）得改进 SM 算法后，再引入结构冗余度计算式（1）～式（3）形成基于SM算法的结构冗余度优化算法，最后依据最终优化模型式（15）按图1所示流程对结构冗余度进行优化.

图1 改进SM算法对结构冗余度的优化流程

3 钢桁架桥算例分析

3.1 钢桁架桥简化模型

取位于密执安的Old North Park Bridge钢桁架桥做优化模型，桥长32m，桥高5.5m，桥身由8段桁架组成，每段长4 m，容许载重10 kN，桁架构件容许应力400 MPa，桥梁构件分为顶梁及侧、桥身弦杆、底梁三类.依照Old North Park Bridge钢桁架桥，缩小2倍得图2所示16节点29杆平面钢桁架尺缩模型，所以桁架模型跨度16m，高2.75m，桥身8段，每段长2m，容许荷载5 kN，左端固定铰约束，右端活动铰约束.杆件截面规格均按《结构用厚壁无缝钢管表》选用，截面尺寸变量（外径、壁厚）按连续变量处理，外径 40～350mm，壁厚 3～15mm.构件弹模200 GPa、泊松比0.3，为便于型钢与圆钢管的比较，对构件截面做圆截面换算和回转半径处理，表1为Old North Park Bridge钢桁架桥的几何性能参数.

图2 平面钢桁架桥有限元模型

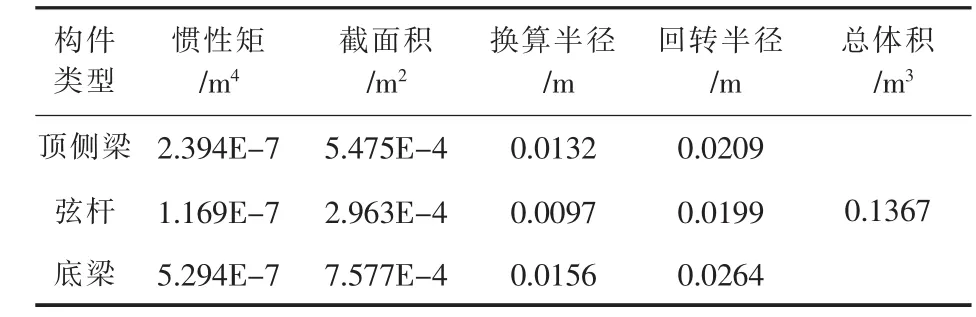
表1 型钢桁架桥中各种构件的几何性能参数

3.2 SM算法对钢桁架桥的截面优化

将图2钢桁架桥构件截面分为顶侧梁、弦杆、底梁三类截面变量，每类变量由Di、ti两个变量组成，即每个解向量Xi0是6维的行向量.根据式（1）～式（15）的描述，得钢桁架桥截面优化数学模型为：

式 （16） 中：fT为终目标函数集合；Tf为结构冗余度、体积的集合函数；T为理想点集合函数；logfTi为终目标第i个分量的自然对数函数；logfli为最小终目标第i个分量的自然对数函数；Di、ti分别为钢管外径、壁厚；eTol为判敛误差限.

取反射系数reflct=1，延伸系数extd=2，缩短系数short=0.5，缩边系数shrnk=0.5，判敛误差限eTol=0.01.图2钢桁架桥在自重和各节点5KN容许荷载的共同作用下经上述改进SM算法循环优化100次后得到图3、图4，表2所示结果.

由图3、图4可知，经SM算法100次循环迭代后各类构件外径、壁厚迭代前后数值趋于一致，即得到了满足终目标函数的构件最优外径、壁厚解.

图3 构件壁厚均值优化趋势

图4 构件外径均值优化趋势

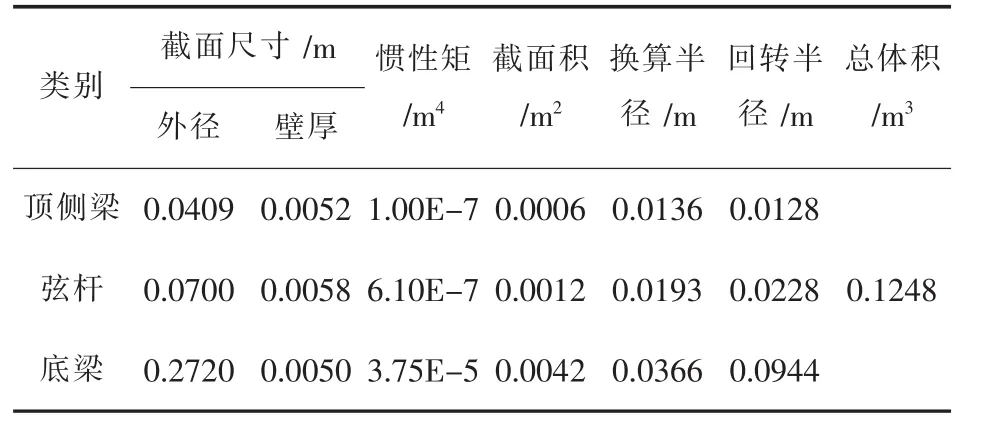
表2 SM算法对构件截面优化设计所得结果

对比表1和表2可知：文中提的改进SM算法设计出的截面优化构件所组成的钢桁架桥比之前按承载力设计的钢桁架桥的用钢量少了0.0119m3；依照《混凝土规范》中长细比与稳定系数、构件承载力成反比的关系，优化后作为主要承载构件底梁的回转半径明显增大，即优化后桥梁的稳定性也有所提高.其中对结构冗余度布置的优化效果如图5所示.

对比图 5（a）、图 5（b）中结构冗余度标准差基准线的取值可知：经改进SM算法优化后，结构冗余度标注差明显减小 （即经改进SM算法优化后，钢桁架桥各构件间冗余度的布置更加均匀）；对比构件1～16所对应的关键构件底梁和顶侧梁的冗余度分布可知：文中所提的改进SM算法对关键构件的冗余度均匀布置效果更加明显.

4 Abaqus对优化结果的分析验证

按表2所示优化后的截面特性，将钢桁架桥在Abaqus中建模，并将表1经过圆截面换算和回转半径处理后的未优化的钢桁架作为对照组，通过二者的仿真分析结果做钢桁架桥的强度、刚度对比分析，结果如图6、图7所示.其中强度按第一强度准则，以容许应力400 MPa作为判别标准；刚度参照《钢结构设计规范》[21]选取跨度的1/400作为判别标准，故文中容许扰度值为40 mm.

图5 钢桁架桥经改进SM算法优化前后的冗余度分布图

图6 钢桁架桥经改进SM算法优化前后的应力分布云图

图7 钢桁架桥经改进SM算法优化前后的位移分布云图

从图6（b）可知，经改进的SM算法设计所得钢桁架桥除非主要受力的顶侧梁外，其他构件应力分布都比较均匀，其中主要承受桥面板与汽车动力荷载的受拉底梁相比其他构件而言，承载能力得到了增强，应力最大值93.81 MPa明显小于构件容许应力400 MPa，即经SM算法设计所得钢桁架桥满足强度要求.从图7（b）可知，经SM算法设计所得钢桁架桥符合简支梁的弯曲特点，其中最大扰曲点（底梁中点）位移值8.562mm明显小于容许扰度值40mm，即经文中所提的改进SM算法截面优化设计所得的钢桁架桥满足刚度要求.

对比图 6（a）和图 6（b）知，经 SM 算法优化设计所得钢桁架桥明显比未经SM算法优化的按构件承载力设计所得结构应力分布要均匀，特别是底梁这种承受桥面荷载的关键构件不会出现应力分布不均的现象；从两图中最大应力值可知，经SM算法优化设计后所得的结构在获得较小用钢量的同时，虽对顶侧梁承载力有所削弱但并不影响结构整体的承载力，反而使得关键构件得到了增强，得到了一种更为合理的结构受力模式.对比图7（a）和图7（b）知，文中提出的基于结构冗余度的改进SM算法做钢桁架桥的截面设计与按传统的按构件承载力做结构的截面设计方法一样，变形形式都满足简支梁的变形特点，虽然经SM算法截面优化所得钢桁架桥的最大位移有所增加，但与按传统的承载力设计方法所得结构的位移在同一个量级（差值在毫米范围），都满足结构设计所需的刚度要求.通过上述对比表明：本文所提的基于结构冗余度的改进SM算法在钢桁架桥截面设计上可行.

5 结 论

文中通过引入结构冗余度、SM算法改进、实例计算和有限元软件的仿真分析，表明了本文提出的基于结构冗余度的改进SM算法在考虑结构整体性能后的截面优化设计方法对于钢桁架桥截面设计的有效性，并得出如下结论：

1）基于响应敏感性的结构冗余度能有效地反映结构的整体承载力，为结构整体性能的优化提供结构层面的一个优化量.

2）结构冗余度在SM算法中的引入，使得做截面优化的同时能充分考虑到结构的受力、变形、稳定性等因素，为优化变量的减少提供了途径.

3）文中提出的基于结构冗余度的改进SM算法跟传统的按构件承载力设计方法一样，对钢桁架桥的截面优化设计同样适用，并且能在满足设计所需的强度、刚度、稳定性要求的同时获得结构的较小用钢量.