各向异性HTI介质中的剪张源矩张量特征研究

唐 杰,张文征,温 雷,李 聪

(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛266071)

1 各向异性HTI介质中的剪张源模型

1.1 含流体HTI介质参数分析

KRIEF等[11]认为,背景各向同性岩石的体积模量K与剪切模量μ和固体基质的体积模量Km与剪切模量μm满足以下关系:

式中:φ是孔隙度。公式(1)和公式(2)是经验速度-孔隙度公式,能够模拟不同孔隙度的岩石弹性特征,即背景各向同性介质的弹性模量参数。

SCHOENBERG等[12]将裂缝当成一个特殊界面来处理,应力通过该界面时是连续的,而位移存在不连续现象。对于含垂直裂纹的HTI介质(图1),可以利用该方法获得干燥岩石的刚度矩阵表达式:

(3)

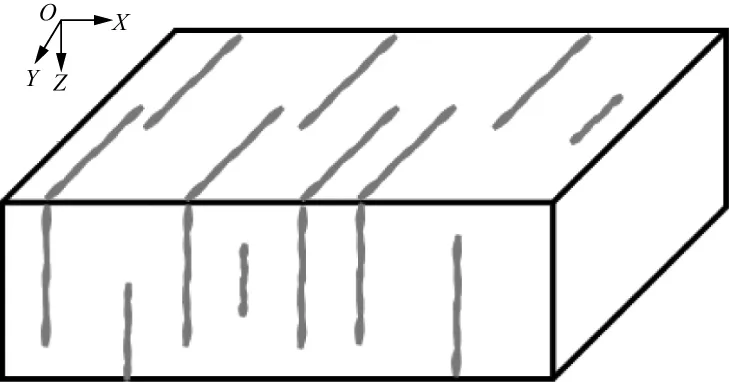
图1 HTI介质图示

式中:Q是纵波模量,Q=λ+2μ,λ是背景各向同性介质的拉梅参数,满足λ=K-2μ/3;ΔN和ΔT分别是法向和切向裂隙弱度,满足ΔN=ZNQ/(1+ZNQ),ΔT=ZTμ/(1+ZTμ),ZN是附加的裂隙法向韧度,ZT是附加的裂隙切向韧度;r=λ/(λ+2μ)。

GASSMANN将各向异性岩石的饱和刚度矩阵表述为干燥岩石刚度矩阵和一个附加的流体影响项,因此利用各向异性GASSMANN方程可以获得饱和各向异性岩石的刚度矩阵各分量[13-14]:

式中:Kfl是孔隙流体的体积模量。

本文采用的模型基质体积模量满足Km=37GPa,基质剪切模量μm=44GPa,基质密度为2.65g/cm3。首先采用KRIEF等[11]给出的方法加入孔隙形成各向同性介质,然后将裂隙参数加入各向同性背景中形成干燥HTI介质。选择水作为孔隙流体,流体密度ρfl=1.02g/cm3,流体体积模量Kfl=2.7GPa,在孔隙和裂缝中加入流体形成饱和HTI介质。图2给出了孔隙度φ=0.2,ΔT=0.2时干燥、饱水HTI介质的参数变化。由图2可知,不同的流体饱和状态会影响纵波速度分布、横波分裂程度和快横波偏振方向,根据横波分裂的观测结果可以反演获得地下裂隙的状态。

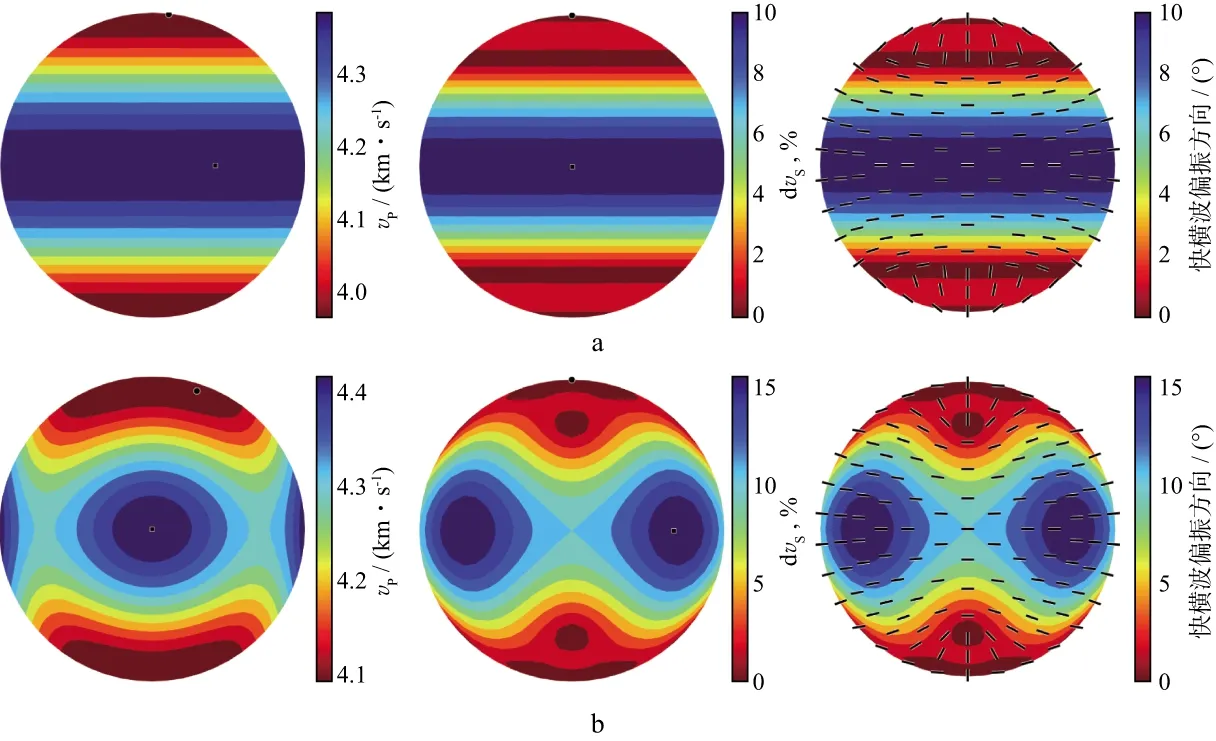
图2 干燥(a)、饱水(b)HTI介质参数变化(φ=0.2,ΔT=0.2)

1.2 HTI介质中剪张源的源张量与矩张量

假定裂纹面的法向方向为n=(n1,n2,n3)T,位错方向为v=(v1,v2,v3)T,图3为剪张源模型的示意图,采用走向角φ、倾向角δ、滑动角θ和张裂角α表示的裂纹面参数满足[15]:

n1=-sinδsinφ,n2=sinδcosφ,n3=-cosδ

(9)

v1=(cosθcosφ+cosδsinθsinφ)cosα-

sinδsinφsinα

v2=(cosθsinφ-cosδsinθcosφ)cosα+

sinδcosφsinα

v3=-sinθsinδcosα-cosδsinα

(10)

走向角φ、倾向角δ、滑动角θ和张裂角α通常是空间位置和时间的函数,为了简化可以忽略其时空变化,将剪张错动近似为点源。走向角、倾向角和滑动角描述了断层面的法向和沿着断层面位错矢量的切向,而张裂角描述了偏离断层面的位错矢量的偏离程度[16-17]。张裂角α∈(-90°,90°),当α>0时代表剪张源,对于纯张裂源,α=90°;α<0代表压裂源,对于纯压裂源,α=-90°;对于纯剪切源而言,α=0。

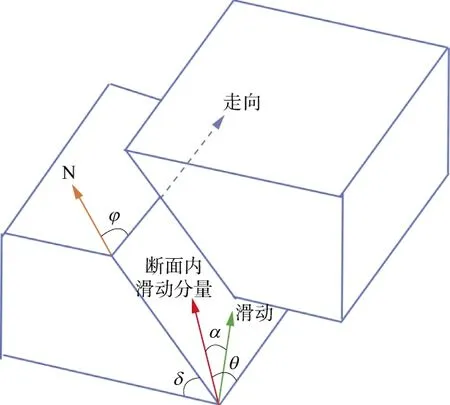
图3 剪张源模型图示

采用裂纹面的法向和位错方向可以获得剪张源的源张量D:

(11)

式中:u是位错矢量的大小,S为断层面积,uS为源强度。

各向异性介质微地震矩张量可以由源张量和震源区介质参数获得:

(12)

式中:Cpqkl(p,q,k,l=1,2,3)为震源区的各向异性刚度参数,四阶弹性张量Cpqkl可以与二阶弹性张量Cij(i,j=1,2,3,4,5,6)相互转化。

2 各向异性HTI介质中的震源特征分析

采用Hudson图可以对微地震震源机制进行分类描述[18]。Hudson图中横坐标表示剪切组分T值,纵坐标表示张性组分k值,T,k的取值范围均为-1～1。此外还可以采用钻石图来表示震源机制中的各个组分[4]。

2.1 矩张量分解

釆用特征值分解法可以将微地震震源矩张量分解为双力偶部分(DC)、补偿线性矢量极偶成分(CLVD)以及各向同性部分(ISO)[19],求取地震矩张量M的特征值和特征方向。设特征值为M1,M2和M3,|M1|≤|M2|≤|M3|,则各向同性分量MISO=(M1+M2+M3)/3。

(13)

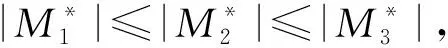
(14)

(15)

对于纯CLVD源,ε=±0.5;对于纯DC源,ε=0;对于膨胀源,ε是正的,对于收缩源,ε是负的。

ISO,DC和CLVD分量在地震矩张量中所占的比例满足[20]:

(16)

其中HISO和HCLVD可正可负,HISO>0代表体积膨胀,相反HISO<0代表体积压缩;HCLVD的正负由ε控制;HDC为正。

2.2 非DC分量变化特征分析

各向异性介质中的矩张量参数依赖于各向异性的类型和强度以及断层面的方向等参数,图4为HTI裂隙介质中由于剪切断裂产生的非DC分量,其中断层面走向30°,倾向角为40°,滑动角为20°,张裂角从-90°变为90°。图4a为Hudson图,其中黑色表示各向同性介质,红色表示干燥介质,绿色表示饱和HTI介质;图4b为各向同性介质中的矩张量分解结果;图4c为干燥HTI介质中的矩张量分解结果;图4d为饱水HTI介质中的矩张量分解结果。由图4 可知饱和介质中的ISO分量和DC分量相对干燥介质有所增加。此外,对于各向同性介质,当张裂角为0时,为纯剪切源,只包含DC分量;而介质为各向异性时,由于震源区介质参数的影响,矩张量中仍然包含非DC分量。研究表明,较小角度的张裂角也会产生较大的非DC分量。

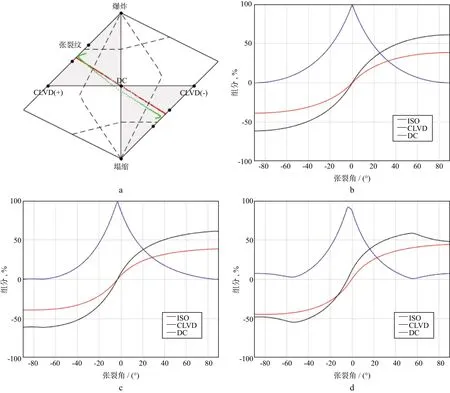
图4 剪张源的源参数(张裂角从-90°到+90°)a Hudson图;b 各向同性介质中的矩张量分解;c 干燥HTI介质中的矩张量分解;d 饱水HTI介质中的矩张量分解

图5给出了背景介质孔隙度变化时的剪张源矩张量分解结果,背景介质孔隙度从0变化到0.3,其中断层面走向30°,倾向角为40°,滑动角为20°,张裂角为10°。可以看出,背景介质孔隙度变化会对剪张源矩张量产生影响。各向同性介质中各分量比例不随孔隙度的变化而变化,而各向异性介质由于背景介质孔隙度的变化会影响各向异性参数,因而会对震源矩张量产生影响。

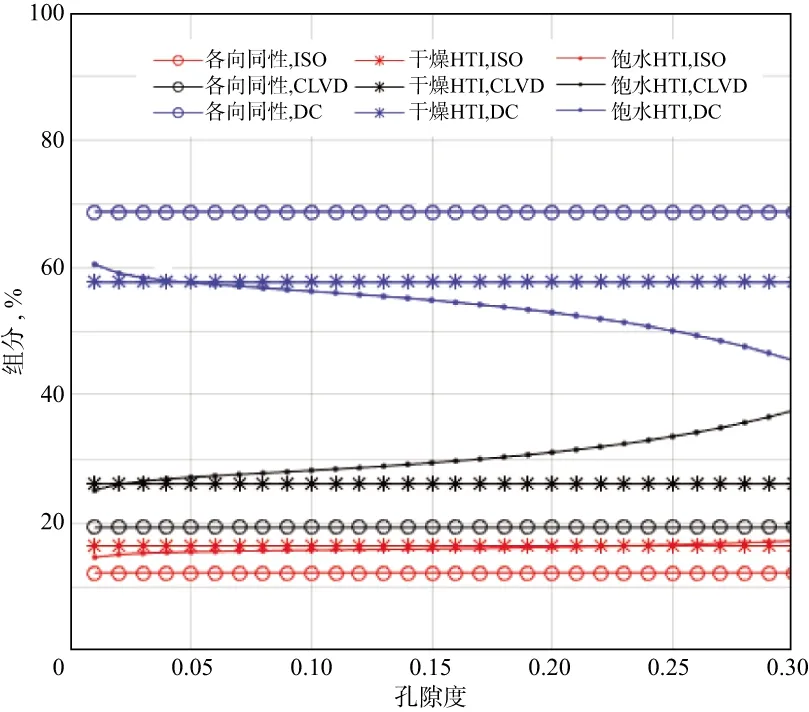
图5 不同孔隙度介质中的剪张源矩张量分解结果(孔隙度为0～0.3)

图6给出了裂隙切向弱度参数变化时的剪张源矩张量分解结果,裂隙切向弱度参数从0变化到0.3,剪张源参数同图5。可以看出,裂隙切向弱度参数变化会对剪张源矩张量产生影响,震源区各向异性介质由于切向弱度参数的变化会影响各向异性参数,因而会对震源矩张量产生影响。

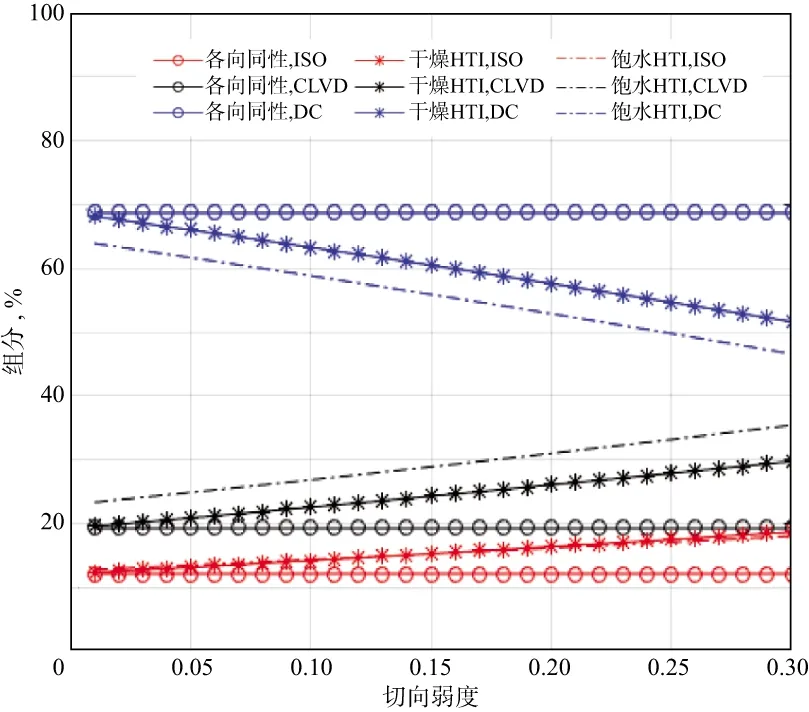
图6 不同切向弱度介质中的剪张源矩张量分解结果(切向弱度ΔT为0～0.3)

3 震源沙滩球与辐射花样分析

3.1 矩张量变化特征分析

图7给出了不同介质中不同张裂角条件下的震源机制沙滩球,从上到下依次为各向同性介质、干燥HTI各向异性介质和饱和HTI各向异性介质,从左到右张裂角分别为0,10°,50°,90°。从图7可知背景介质会对震源沙滩球中的极性分布产生影响。

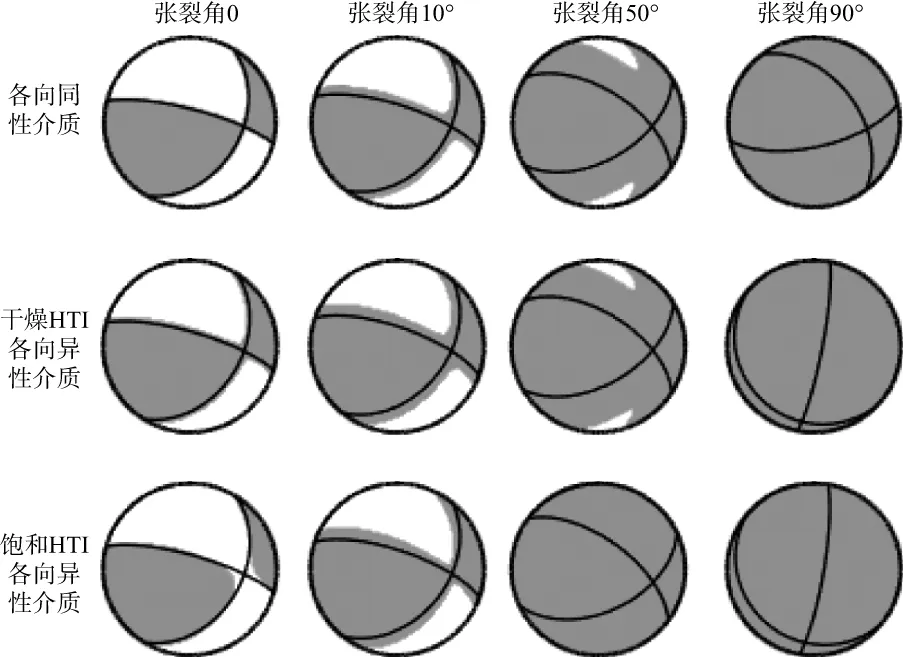
图7 震源机制沙滩球

3.2 各向异性介质中张裂源的辐射花样

依据HTI介质各向异性地震矩张量解析表达式,结合Aki和Richards公式,计算了远场P波辐射花样[21],如图8所示。需要说明的是,这里的计算假定了传播介质是全空间各向同性,而震源区是各向异性介质。图8中的断层面走向30°,断层面倾角40°,断层面滑动角为20°,从上到下依次为各向同性介质、干燥HTI各向异性介质和饱和HTI各向异性介质,从左到右张裂角分别为0,10°,50°,90°。

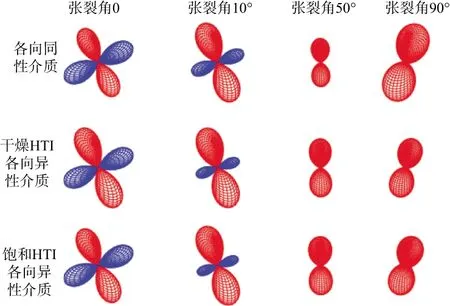
图8 P波辐射花样

4 结束语

本文分析了含裂隙干燥和饱和HTI介质的弹性参数以及各向异性HTI介质中的剪张源矩张量与微地震矩张量,比较了震源区为各向同性介质、干燥和饱水HTI各向异性介质情形下的剪张源震源机制与地震矩张量沙滩球,研究了震源区HTI各向异性对双力偶分量(DC)、补偿线性偶极子分量(CLVD)和各向同性分量(ISO)的影响以及各向异性HTI介质中剪张源的辐射花样。研究结果表明,各向异性介质中的矩张量参数依赖于各向异性的类型和强度以及断层面的方向等参数。研究各向异性矩张量能够提供震源区的各向异性信息,有利于了解地震如何破裂和扩展,具有重要的价值和应用前景。