基于优化fastICA盲源分离算法的地震属性融合方法研究

邱 玥,孙成禹,唐 杰

(中国石油大学(华东)地球科学与技术学院,山东青岛266580)

目前地震属性融合方法大致分为人工叠合、基于属性颜色融合和基于属性数据融合3类方法。人工叠合法操作简单但精度较低,对信息的综合处理及分析能力较差;基于属性颜色融合法以RGB技术[1-2]为代表,充分利用了地震属性中地质构造和岩性变化信息,但无法消除属性间的冗余信息;基于属性数据融合法包括多元线性回归、人工神经网络、独立分量分析等。这些方法直接对由数学统计和人工智能等手段提取得到的最优属性数据进行融合,能够获得更高精度和更可靠的融合效果。

与主成分分析(principal component analysis,PCA)方法相比,独立分量分析(independent component analysis,ICA)算法主要针对数据的高阶统计特性,能够有效地去除高阶统计特性中的冗余信息,更好地揭示数据的本质结构[3-4]。ZARZOSO等[5]提出了以最小互信息(minimum mutual information)为目标函数的方法。BELL等[6]提出了名为Informax的自适应算法,该算法通过选择逼近源信号概率分布的最佳非线性函数来有效地恢复源信号分量。YUAN等[7]提出了极大似然目标函数与非线性PCA方法。HYVARINEN等[8]提出了以峰度为目标函数的一种快速独立分量分析(fastICA)算法。普艳香[9]将fastICA算法引用到地震多属性分析中。李小霞[10]研究了ICA算法在宽频带数据谱融合中的应用。上述方法都未针对含噪地震属性融合进行研究。

本文采用具有鲁棒性强、统计特性明确的负熵近似[11]作为目标函数。避免了上述方法中目标函数复杂、非线性函数选取困难的缺点。目标函数的优化方法选用基于固定点迭代理论的fastICA算法,通过快速寻优迭代找出非高斯性最大值。避开了常规ICA梯度算法[12]需要选取参数和步长的步骤。同时对初值采取降敏感性处理,选取具有5阶收敛速度的迭代公式提高迭代稳定性,减少迭代发散的可能性。引入满足非高斯分布且实用性较强的贝叶斯阈值函数对含噪属性数据进行随机噪声压制,改善了fastICA模型对含噪属性数据去噪效果不显著的局限性,进一步提高了融合资料的品质。最后用理论模型数据及实际地震资料进行了应用测试。

1 基本原理

1.1 地震属性融合的fastICA算法

当输入信号处于未知状态,且信号传输所处环境亦未知的情况下,仅依据仪器检测到的混合信号估计出源信号,是盲源分离技术研究的内容[13]。针对某一目标储层,假设最终观测得到的地震属性是表征目标储层特征的各种岩性、物性、含流体性质参数的线性混合,将这些储层特性参数等效为输入的未知源信号,借鉴盲源分离思想,可将这些混合特征参数恢复成相互独立的成分。

本文采用fastICA算法进行盲源分离。经过该算法得到的属性数据分量间去掉了高阶相关性,实现各分量的统计独立[14]。利用fastICA算法进行地震多属性融合的思想来源于多源信息融合,将由不同仪器模式或采集技术得到的二维地震属性等效成图像。为了加快算法处理效率,首先将根据任务目标选择出的地震属性数据进行平滑分块,并从中随机挑选出不少于1000的属性块作为fastICA算法输入[15];然后利用优化的fastICA基函数完成属性数据块从空间域至ICA域的映射,并在ICA域中利用构造的贝叶斯阈值函数和4种效果不同的图像融合规则对含噪声属性数据进行去噪和融合;最后将经过随机噪声压制的融合地震属性数据映射回空间域。

1.2 融合规则

不同的融合规则对应于不同的数据取舍,均值融合规则侧重于保持数据背景信息,最大绝对值融合规则主要保持数据边界特征,加权融合规则是最大绝对值融合规则的拓展,而基于区域的融合规则综合了最大绝对值和均值两种融合规则。针对具体目标要求,可以选择不同的融合规则。

1) 均值融合规则。

(1)

2) 最大绝对值融合规则。

(2)

3) 加权融合规则。

对第i个属性块数据,以其在变化域中均值作为指示因子,计算其权值:

(3)

则融合表达式为:

(4)

某些情况下,权值wi的分母可能很小,会导致计算的数值不稳定,此时可对这些属性块采用均值融合规则或最大绝对值融合规则。

4) 基于区域的融合规则。

(5)

mi=1的区域采取保持边界特征的最大绝对值融合规则或加权融合规则;mi=0的区域采取保持背景信息为主的均值融合规则[16]。上述公式求取的是第i个属性块的融合结果,按此方法类推,便能求出所有属性块在ICA域的融合结果。

2 fastICA算法优化

fastICA算法能够从多维数据中寻找出暗含在混合信号中彼此独立的成分并使此种统计意义上的独立性最大化[17]。假设t时刻观测得到的混合信号为:

(6)

式中:X代表在时刻t经观测获取的线性混合信号;S代表原始信号;A代表混合矩阵。目标是根据唯一已知的X分离或估算出S[18]。通常无法得知混合系统的特征,故允许比例不定性及顺序不定性现象存在。当计算出的矩阵A存在逆矩阵时,只要源信号数据满足非高斯性的前提条件成立,便可以估算A的逆矩阵W,经公式:

(7)

得到彼此之间完全独立的估计源信号数据Y,Y是源数据S的最优逼近。首先,需要对观测数据进行预处理,包括零均值化及白化处理。其中白化处理通过PCA算法[19]实现:

(8)

在快速寻优的过程中,本文选用负熵的近似作为目标函数:

(9)

式中:J(·)表示求负熵,即目标函数;E[·]表示求变量均值;g(·)代表非二次型函数,其表达形式有很多,本方法选用g(Y)=-(1/4)Y4;Yg是高斯随机变量。目标是求(9)式最大值,等效于找出(7)式中具有最大非高斯性的分离矩阵W。为了提高迭代计算速度,采用具有5阶收敛速度的改进迭代公式[20-21]:

(10)

式中:g′(·),g″(·)分别代表g(·)的一阶和二阶导数。

(11)

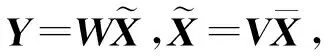
(12)

利用fastICA基及其逆矩阵可实现地震属性数据空间域与ICA域的相互映射。但是传统的ICA算法对随机噪声压制效果不强。因此,利用贝叶斯方法构造出满足非高斯分布的阈值函数在ICA域中对随机噪声进行去噪处理。贝叶斯阈值函数相较于常规的硬阈值等函数来说更符合地震数据特征的分布规律,对随机噪声具有更好的压制效果。

假设有效信号S中混入了均值为0,方差为σ的高斯白噪声N,则接收到的观测数据Z可以表示为:

(13)

h(zi)=

(14)

综合上述算法,基于优化fastICA的地震属性融合流程如图1所示。

图1 基于优化fastICA算法的地震属性融合流程

3 模型测试与实际资料效果分析

3.1 优化基函数模型测试

选取图2所示的4个信号作为原始信号,将其通过随机产生的矩阵,经线性变换得到如图3所示的混合信号。分别采用传统fastICA算法和对初值进行降敏感性并具有5阶收敛速度的优化后的fastICA算法进行分离,得到的信号如图4和图5所示。

计算两种方法分离出的有效信号的波形相似度和信噪比,结果如表1所示。可以看出,采用优化后的fastICA算法分离得到的信号,波形相似度和信噪比都有了一定的提高。

同时,比较运行10次后得到的平均迭代次数,fastICA平均迭代次数为19.20次,方差为5.156,而优化后的算法平均迭代次数为16.80次,方差为2.56,说明优化后的算法收敛性更强,稳定性更高。

3.2 实际属性数据对比分析

3.2.1 实例一

图6为提取的某河道砂体的平均峰值振幅、总能量、均方根振幅和相干体4种含噪属性,其中图6a,图6b和图6c的振幅类属性中椭圆位置表明地层中发育古河道,且含有一些砂体信息。图6d的相干体包络反映了河道的边界信息,具有前3个属性不具备的特有信息。图7是经fastICA处理后得到的4种地震属性数据。图8是利用图像融合中最大绝对值融合、均值融合、加权融合和基于区域融合4种不同融合规则对图6中4种地震属性进行融合后的数据。图9是加入贝叶斯阈值函数对原始各单一属性进行去噪处理后再利用融合规则进行融合的结果。图8和图9中色标代表经归一化处理后各融合规则下融合数据的相对大小。

图2 原始信号

图3 混合信号

图4 采用原始fastICA算法分离出的信号

图5 采用优化fastICA算法分离出的信号

表1 算法性能比较

图9与图8相比,随机噪声得到明显压制,剖面的清晰度变高,有效信息得到凸显。将融合后的地震属性(图9)与原始单一属性(图6)进行对比,发现图9 中蕴含更多的地质信息,既能显示出河道的内部变化特征,又能突出其边界特征,类似于给河道进行了镶边处理,更能多角度地反映出目标地质体的响应特征。对比4种不同的融合结果可以发现,这种镶边效果在取最大绝对值融合结果(图9a)中尤为明显,主要是因为取最大绝对值融合规则侧重于保持边界信息,故突出保留了河道的边界特征,但该规则忽略了常值背景中的信息,使得融合后的地震资料中河道内部信息不明显。取均值融合(图9b)则保留了河道内部的信息,融合后的结果较为平滑,由于其边缘信息过度平滑,所以并没有出现镶边效果。加权融合规则(图9c)是对上述两种融合规则的综合,融合后的结果较为折中,但是该算法不能考虑数据中目标的特性,而一般数据中的目标轮廓是不规则形状,所以有时会引起融合图像中背景对比度下降,造成融合图像对比度低于原始图像数据对比度。而基于区域的融合规则(图9d)在融合过程中对数据中的边界和背景信息分别采用与之相适应的融合规则,使最终的融合结果中综合了背景及边界的信息,更能体现数据中目标的特征。对比图9c和图9d黑色虚线框中的部分也可看出针对该数据基于区域的融合规则效果更好。

图7 经fastICA处理后的4种地震属性a 平均峰值振幅;b 总能量属性;c 均方根振幅属性;d 相干体属性

图8 不同融合规则下的融合效果(实例一)a 最大绝对值融合;b 均值融合;c 加权融合;d 基于区域融合

3.2.2 实例二

图10为XQ工区内选取的总能量和相干体属性(含噪声),其中总能量属性展示了该工区内砂体空间分布情况,相干体属性展示了该工区断层分布情况。仅通过fastICA处理图10中的两种属性而不加入融合规则时得到图11所示结果。在传统fastICA算法和加入阈值去噪函数的优化fastICA算法下采用不同融合规则对总能量属性和相干体属性进行融合,分别得到图12和图13所示结果。

由图11可看出,经fastICA处理,能将反映地质体本质特征的源参数特征从属性空间中提取出来。但是仅由fastICA处理的数据,图11a中椭圆部分缺少断层信息,图11b中又不能准确描绘砂体边界,所以需要加入融合规则进一步综合地质信息。由图12和图13可以看出,加入融合规则后,不仅能同时得到砂岩与断层的地质信息,较为清晰地反映研究区域中砂岩与断层的相互切割关系,而且与图11相比砂体的范围描述更加精确。图13d中绿色虚线代表砂体区域,黑色虚线代表断层分布。对比图12与图13可以明显看出,图13中包含的噪声更少。同时,为了验证优化fastICA算法对随机噪声的压制效果,对基于区域融合规则下的数据选用硬阈值、软阈值函数与该优化方法进行对比,所得峰值信噪比参数见表2。

表2 含噪属性融合性能对比

表2中峰值信噪比参数表明,优化fastICA算法融合后的结果中随机噪声较硬阈值和软阈值去噪方法更少,该方法对随机噪声的压制效果更好,能够获得品质更高的地震属性融合结果。对比图13中4种融合规则的融合效果,可以看出,图13b比图13a更注重背景信息,缺少细节信息;而图13c和图13d效果类似,都是图13a和图13b的折中表现,只是图13c在断层分布和融合数据的上部常值背景中对比度较图13d稍差,所得结论与实例一相似。

图9 去噪后不同融合规则下的融合效果(实例一)a 最大绝对值融合;b 均值融合;c 加权融合;d 基于区域融合

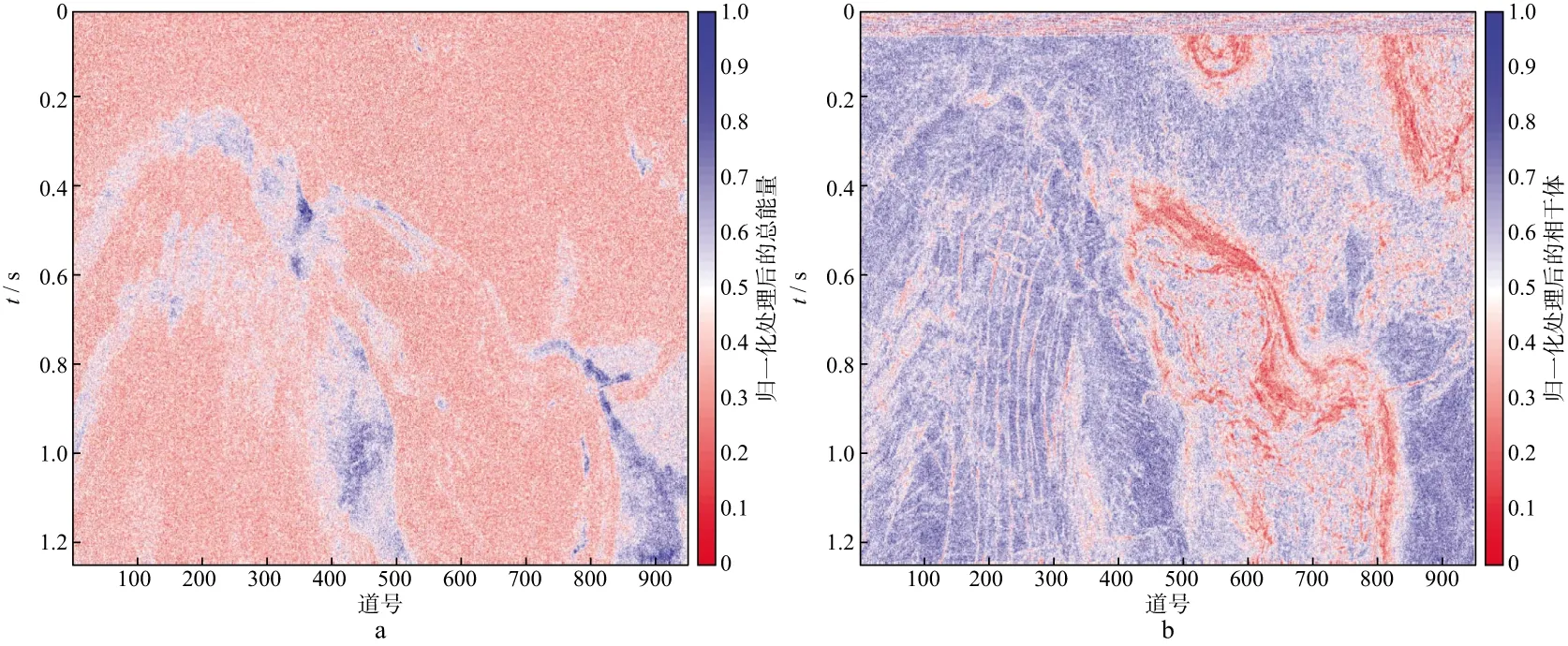
图10 XQ地区总能量属性(a)和相干体属性(b)

图11 采用fastICA对XQ地区总能量属性(a)和相干体属性(b)进行处理的结果

图12 不同融合规则下的融合效果(实例二)a 最大绝对值融合;b 均值融合;c 加权融合;d 基于区域融合

图13 去噪后不同融合规则下的融合效果(实例二)a 最大绝对值融合;b 均值融合;c 加权融合;d 基于区域融合

4 结论

本文将基于优化fastICA盲源分离的算法引入地震属性融合技术中,得到了以下结论。

1) 优化后的fastICA算法在迭代次数、波形相似度和信噪比方面都有一定的提高,而且突出了地震属性间的高阶统计特征,是分解混合观测数据中所蕴含的独立信息的一种有效方法。

2) 地震属性数据资料试验结果表明,经优化fastICA算法融合后,资料中基本包含了单一属性所蕴含的地质信息,更有利于突出与研究目标相关的地质特征,从而使研究人员能多角度、全方位地观察目标体的响应特征。

3) 优化fastICA算法在实现地震属性融合的过程中对随机噪声具有较好的压制效果,能得到较高信噪比的地震属性融合数据,而不必再采用其它去噪算法对融合后的地震数据进行去噪处理。算法快速稳健,运用方便,具有十分良好的应用前景。

4) 不同的融合规则对应于不同的融合效果,取最大绝对值融合注重边界信息,取均值融合注重背景信息,加权融合和基于区域融合是取最大绝对值和均值融合的折中表现,但鉴于加权融合有时会降低融合图像中背景对比度,故建议使用基于区域的融合规则。