富有机质泥页岩岩石物理横波速度预测方法研究

张秉铭,刘致水,刘俊州,包乾宗,折向毅,夏红敏,刘兰锋

(1.中国石油化工股份有限公司油田勘探开发事业部,北京100728;2.长安大学地质工程与测绘学院,陕西西安710064;3.中国石油化工股份有限公司石油勘探开发研究院,北京100083;4.西北有色勘测工程公司,陕西西安710000)

横波测井速度是叠前地震资料反演、脆性因子计算、应力分析、储层预测的基础数据之一[1-4]。受限于测井成本及技术,实际研究中经常缺乏横波测井数据。为解决此问题,地球物理研究人员利用相关的数学方法和常规测井资料预测横波速度。横波速度预测方法主要分为3类:经验关系式法[5-7]、岩石物理模型法[2-4,8-10]以及神经网络法[11]。经验关系式法是基于实验室测量数据或测井数据,拟合横波速度与纵波速度(或者孔隙度、泥质含量等参数)之间的线性或者简单非线性关系,再利用此关系预测横波速度;神经网络法是根据大量的多种测井数据,由神经网络训练得到横波速度与其它测井数据的强非线性关系,再根据此关系预测横波速度;岩石物理模型法则是基于波在介质中的传播过程,根据岩石的物质成分和结构,构建能够表征岩石微观特征参数与弹性参数之间关系的数学公式,再利用此公式预测横波速度。对比3类方法可以发现:①经验关系式法和神经网络法依赖于输入的数据样本,当输入数据样本的质量不高时,则无法获得可信的预测结果;②经验关系式法和神经网络法只能代表输入数据样本的规律,没有明确的物理意义,可推广性差;③岩石物理模型法的基础是波传播理论,具有明确的物理意义而与输入数据无关,针对某种岩石物理特征提出的模型可自然推广应用于具有类似岩石物理特征的储层。因此,基于岩石物理模型的横波速度预测方法已经成为石油与天然气勘探工业中的主流横波速度预测方法。这类方法中,针对碎屑岩[3,8-11]和碳酸盐岩[12-15]等常规储层的研究较多,针对泥页岩[16]的研究相对较少,而针对非常规富有机质泥页岩[2,17-19]的方法研究则更少。复杂的矿物组成、孔隙结构以及有机质的存在使得在常规储层中应用效果较好的方法不能很好地应用于富有机质泥页岩。从岩石物理理论角度来说,针对多矿物组成及复杂孔隙结构的相关研究较为成熟[1-4,8-15],而针对干酪根的研究则极少。干酪根的体积模量和剪切模量都较小[1,18],其数值接近于盐水,与矿物差别较大;但是干酪根与盐水又有根本的不同,即干酪根是具有剪切模量的固体,而盐水是没有剪切模量的流体。针对这一问题,有两种解决思路:一些学者[17-19]在构建富有机质泥页岩的岩石物理模型时将干酪根等效为固体颗粒,通过使用含有包含物的模型来考虑干酪根对岩石速度的影响,这就需要能够同时考虑固体和流体包含物、又不受“稀疏”含量包含物限制的岩石物理模型[18]。另一些学者[2]则将干酪根等同于流体,利用类似流体替代的固体替代理论将干酪根加入岩石中,从而计算富有机质岩石的弹性参数。

本研究的地质目标是鄂西渝东地区建南构造侏罗系下统自流井组东岳庙段富有机质泥页岩,针对目标层钻探的J111井及JYHF-1井均获得工业气流,与这两口井邻近的多口老井在该段见良好的天然气显示。该套页岩气有利地层在区内分布稳定,一般为130～200m,普遍含有一定的有机质,自底至顶大体可分为两个层段:下层发育大套灰黑色页岩、泥岩夹少量介壳灰岩薄层;上层发育灰黑色页岩、泥岩,其中含较多的灰质、砂质成分,并且含大量薄层状介壳富集层[20]。整体来看,该段地层矿物复杂(主要包含粘土、石英、方解石、长石),含有机质,孔隙结构复杂(主要包含裂缝、粒间孔、生物孔),目前尚无较好的针对此类地层的岩石物理横波速度预测方法。针对建南构造侏罗系东岳庙段的富有机质泥页岩特征,以Keys-Xu岩石物理模型[21]为基础,引入Gassmann方程[23]、Voigt-Reuss-Hill(VRH)平均公式[1]、Wood方程[1]、Brown-Korringa固体替代技术[24]及Berryman的特殊孔隙理论[22],提出了一种考虑多矿物、复杂孔隙类型和有机质(干酪根)含量的富有机质泥页岩岩石物理模型,在纵波速度的约束下预测富有机质泥页岩的横波速度。

1 理论基础

富有机质泥页岩岩石物理横波速度预测方法是基于Keys-Xu岩石物理模型、Gassmann方程、Brown-Korringa方程、Berryman的三维特殊孔隙理论等构建的模型,本节对这几种重要的基础理论进行介绍。

1.1 Keys-Xu岩石物理模型

Xu-White模型[3]是目前工业界应用最为广泛的岩石物理模型,该模型针对泥质砂岩提出,后被推广到碳酸盐岩[4,14]和富有机质泥页岩[18]。Xu-White模型的核心技术在于将微分等效思维应用到Kuster-Toksöz理论中,通过多次迭代以求取包含刚性孔隙与柔性孔隙的干岩石的体积模量和剪切模量,该技术虽然很好地解决了Kuster-Toksöz理论[8]不适用于大孔隙度岩石的问题,但是存在计算量大的缺陷。针对这一缺陷,KEYS等[21]提出了一种干岩石情况下的Xu-White模型近似公式,本文称之为Keys-Xu模型,Keys-Xu模型能够使计算结果与Xu-White模型基本一致的情况下,避免了Xu-White模型较大计算量的问题。Keys-Xu岩石物理模型的公式为:

式中:φ为孔隙度;K0,G0分别为岩石基质的体积模量和剪切模量;K(φ),G(φ)分别为含孔隙干岩石的体积模量和剪切模量;P,Q分别为干孔隙对岩石体积模量和剪切模量的影响因子[22],统称为形状因子。Keys-Xu岩石物理模型使用WU的孔隙理论[25]描述孔隙对岩石弹性性质的影响,该理论将岩石中的孔隙等效为椭球体,使用椭球体的短长轴之比(孔隙横纵比α)描述孔隙的形状及其对弹性性质的影响:孔隙横纵比α在0～1之间,α越接近于0表示孔隙越扁(裂缝状孔隙),岩石速度降低;α越接近于1则表示孔隙越趋于圆形(球形孔隙),岩石速度增加。WU的椭球形孔隙假设与实际岩石中真实的复杂孔隙形态差别较大,且公式较为复杂而不易应用。针对该问题,BERRYMAN[22]提出了四种特殊孔隙形态(球形、针形、硬币状、裂缝状)的形状因子来描述岩石中的复杂孔隙结构与弹性参数之间的关系,其中裂缝状孔隙的物理意义与Wu的理论近似,但是其公式要比Wu的公式简单。LIU等[9]证明,含针形孔隙岩石的速度低于含球形孔隙岩石的速度,且二者近似于含孔隙横纵比为0.3的裂缝状孔隙岩石的速度,多个研究[9,15]证实,将岩石中的孔隙等效为球形孔隙与裂缝状孔隙的组合,通过二者体积比的变化能够有效描述岩石中复杂的孔隙形态,获得较为准确的速度,因此本文选择Berryman三维孔隙理论中的球形孔隙、裂缝状孔隙来描述富有机质泥页岩中的复杂孔隙系统。在基质m中加入包含物i时,令球形孔隙或球形包含物对岩石体积模量和剪切模量的影响因子为Ps和Qs,硬币状裂缝孔隙或裂缝状包含物对岩石体积模量和剪切模量的的影响因子为Pc和Qc,则公式(1)和公式(2)中的P=Ps+Pc,Q=Qs+Qc。Ps,Qs,Pc,Qc的公式分别为公式(3)、公式(4)、公式(5)、公式(6)。

式中:β=G(3K+G)/(3K+4G);ζ=G(9K+8G)/6/(K+2G);α为硬币状包含物的横纵比;下标m,i分别表示基质和包含物。在岩石物理模型中,假设包含物随机分布,以使其等效为各向同性。当需要计算干岩石的体积模量和剪切模量时,则将包含物模量(Ki和Gi)设为0,当需要计算流体饱和岩石的体积模量和剪切模量时,则将包含物的剪切模量(Gi)设为0。

1.2 Gassmann方程

Keys-Xu模型是在干岩石(孔隙中不含流体)条件下推导得到的。要获得饱含流体岩石的弹性参数,则需要利用流体替代技术向孔隙中加入流体,即利用Gassmann方程由干岩石速度预测饱和流体岩石速度。Gassmann方程适用于低频情况,即当波的频率足够低时,孔隙流体具有充分的时间流动而且波动没有诱发孔隙压力产生梯度变化时才成立。Gassmann方程的公式为[23]:

式中:Ks,Kd,K0,Kf分别为饱和流体岩石、干岩石、岩石基质及孔隙流体的体积模量;Gs和Gd分别为饱和流体和干岩石的剪切模量;φ为孔隙度。

1.3 Brown-Korringa固体替代理论

BROWN等[24]利用岩石弹性张量表示Gassmann方程,提出了各向异性流体替代理论。该理论经过简单的改造就可以用来将岩石中的固体替换为另一种固体,即进行固体替代。由于干酪根的弹性参量不同于固体也不同于流体的独特性质,本文利用固体替代理论将干酪根加入岩石中。固体替代公式为:

(9)

式中:Se,Sd,S0分别为富有机质岩石、干岩石、岩石基质的四阶柔度张量;Vk为干酪根体积含量;Sφ和Sk分别为孔隙空间及孔隙空间填充的干酪根的四阶柔度张量;柔度张量的下标i,j,k,l,m,n,p,q分别在整数1～3之间变化。

2 基于Keys-Xu模型的富有机质泥页岩横波速度预测流程

根据富有机质泥页岩的特征,本文将其等效为基质矿物、干酪根、含流体孔隙组成的混合物(图1)。其中岩石基质矿物等效为石英、方解石、长石、干黏土四种;总孔隙度被等效为由裂缝状孔隙(黏土湿裂缝和有效孔隙中的裂缝体积之和)和球形孔隙组成,球形孔隙与裂缝状孔隙体积分数自适应变化,以此来描述岩石中复杂的孔隙类型。与Xu-White方法一样,本文的富有机质泥页岩横波速度预测流程由多个岩石物理模型组合来构建(图2),详述如下。

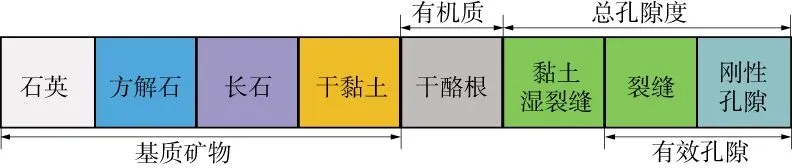
图1 等效富有机质泥页岩岩石物质组成

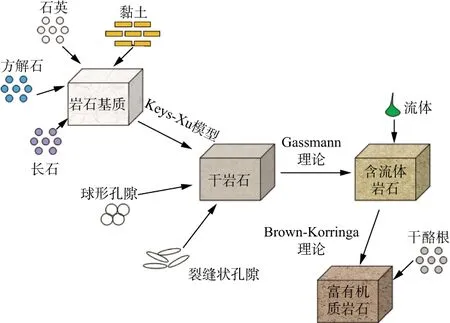
图2 富有机质泥页岩岩石物理速度预测流程

1) 使用VRH平均公式[1]计算岩石基质(混合矿物)的弹性模量:

(10)

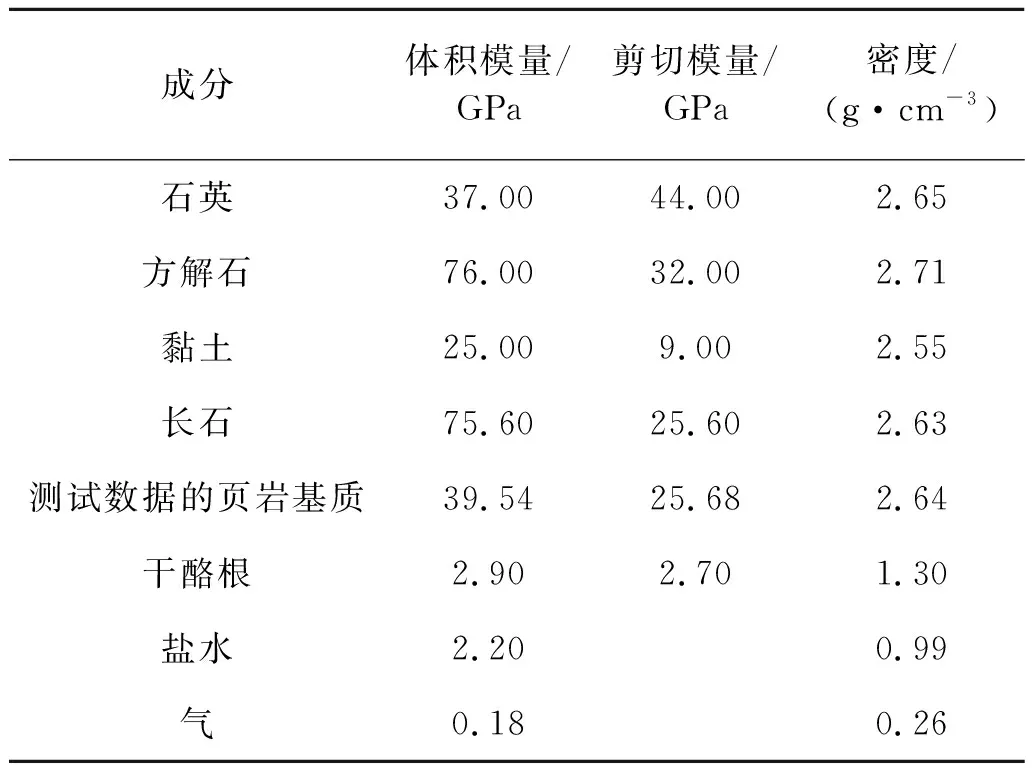
表1 岩石组成成分的弹性参数和密度[1]

2) 利用Keys-Xu岩石物理模型(公式(1)和公式(2))计算含干孔隙岩石(干岩石)的体积模量Kd和剪切模量Gd,其中孔隙由球形孔隙与裂缝状孔隙组成,总孔隙度由测井解释得到[24]。

3) 利用Wood方程计算混合流体的体积模量Kf,公式为:

(11)

式中:Kg和Kw分别为气和水的体积模量;Sg和Sw分别为含气和含水饱和度,由测井解释得到[24],Sw+Sg=1。

4) 利用Gassmann方程(公式(7)和公式(8))计算饱和流体泥页岩的体积模量Ks和剪切模量Gs。

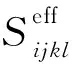
6) 最后,利用纵、横波速度与弹性参数之间的关系计算饱和流体岩石的纵、横波速度,公式为:

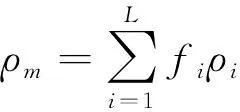
这样,就建立起了纵、横波速度与可变的孔隙参数(球形孔隙体积分数φs和裂缝状孔隙分数φc,φs+φc=1)之间的关系。在横波速度预测过程中,通过使计算和实测的纵波速度vPc,vPm之差的绝对值达到极小值(表示为ε)来建立目标函数:

(14)

采用迭代算法求解公式(14)以反演得到孔隙参数(φs和φc)。再将φs和φc代入图2所示的流程中(从第②步骤代入)计算横波速度vSc。

3 应用

将本文所构建的富有机质泥页岩岩石物理横波速度预测方法应用于实验室测量数据与测井数据,在纵波速度的约束下求取横波速度。为了定量评价横波速度预测方法的准确性,计算实测结果与预测结果之间的均方根误差(dRMSE)和线性拟合相关系数R2,分别为公式(15)和公式(16)。

(15)

(16)

3.1 实验室数据

利用VERNIK等[26]在实验室针对饱和盐水岩石超声测量的数据(70MPa围压环境)测试了本文提出的富有机质泥页岩岩石物理横波速度预测方法。测试时使用了其测量的20个岩石样品数据里的19个,未使用纵、横波速度较高的1个样品。19个样品的干酪根含量为1.4%～36.3%,孔隙度为0.97%～30.90%。

图3对比了利用前述速度计算流程正演的结果与实验室的测量结果[26],其中红线表示基质中加入2%的干酪根,纵、横波速度随孔隙度(0～40%,含盐水孔隙)的变化曲线,黑线表示基质中加入35%的干酪根,纵、横波速度随孔隙度(0～40%)的变化曲线。从上到下的六条红线和黑线分别为球形孔隙体积比(φs)为100%,80%,60%,40%,20%,0,相应的裂缝状孔隙体积比(φc)则为0,20%,40%,60%,80%,100%时的变化曲线。彩色圆点为VERNIK等[26]实际测量数据,颜色表征干酪根含量。由图3可知:当孔隙度不变、干酪根含量增加时,岩石的速度降低;在干酪根含量不变、孔隙度增加时,岩石的速度降低;随着球形孔隙含量的降低,岩石的速度降低。由图3可知,通过孔隙度、干酪根含量的变化,可以覆盖所有数据点,即新模型可以解释测量数据的孔隙度—干酪根含量—速度之间的关系。

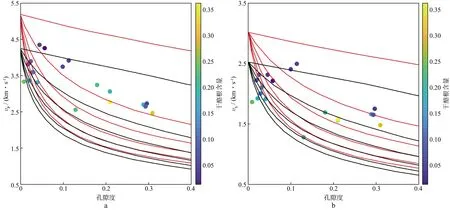
图3 基于富有机质泥页岩岩石物理横波速度预测方法的纵波速度(a)和横波速度(b)正演结果与实测数据

利用所构建的横波速度预测流程预测VERNIK等[26]数据的横波速度,并将预测速度与实测数据进行对比以测试本文方法的有效性。图4为预测速度与实测速度的交会图,表2为预测纵、横波速度的均方根误差和拟合相关系数统计。图中位于红色对角线上的数据点代表预测速度与实测速度之间吻合度高。由图4及表2可见:①预测的纵波速度与实测纵波速度基本吻合,计算的dRMSE为0.0199,R2为0.9989,说明预测的纵波速度与实测数据几乎完全一致,其原因在于纵波速度在计算过程中是约束量;②总体上,预测的横波速度均匀分布于红色对角线两边,计算的dRMSE为0.0945,R2为0.9439,说明实测数据与预测数据吻合率较高。个别点离红色对角线稍远,其原因是所取的基质参数与该数据点的实际情况差别较大,孔隙度、孔隙类型、干酪根含量的变化不足以消除这种影响,这说明在实际应用中,需要根据具体的研究对象选择基质参数。

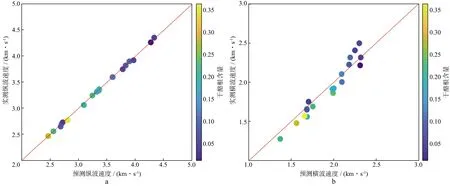
图4 预测速度与实测速度交会a 纵波速度;b 横波速度

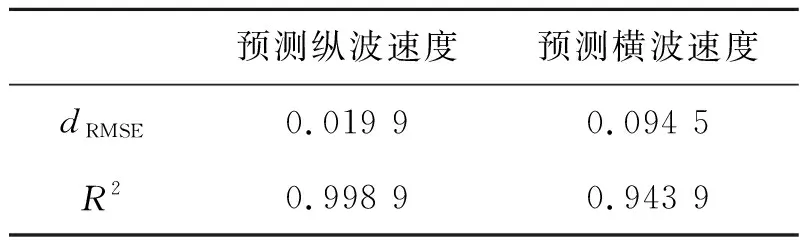
表2 预测纵、横波速度的均方根误差与拟合相关系数统计

图5a和图5b分别是计算的球形孔隙及裂缝状孔隙体积分数与孔隙度的交会图;图5c和图5d是计算的球形孔隙及裂缝状孔隙体积分数与干酪根含量的交会图。由图5a和图5b可见,随着孔隙度的增加,球形孔隙的体积分数呈非线性增加趋势,裂缝状孔隙的体积分数呈非线性降低趋势,由这些数据点拟合孔隙度和球形孔隙体积分数、孔隙度与裂缝状孔隙体积分数之间的关系,发现所计算的球形孔隙和裂缝状孔隙的体积分数与孔隙度呈对数关系,公式显示在图中。由图5c和图5d可见,所求得的球形孔隙和裂缝状孔隙的体积分数与干酪根并无特别的关系。

3.2 油田实际数据

将本文方法应用于建南构造页岩气区域A井侏罗系东岳庙段地层的横波速度预测。图6显示了该井目的层段的录井岩性、储层位置、测井解释结果、孔隙类型计算结果,纵、横波慢度(速度的倒数)的实测与预测结果。录井资料显示,该井目的层段下部(约612～645m)以页岩为主,上部(约525～612m)以泥岩为主。根据多矿物测井解释方法[27]估算矿物含量、孔隙度、含气饱和度,其中测井解释矿物主要包括石英、长石、方解石、黏土。根据CARBOLOG方法[28]求算干酪根体积分数,结果显示干酪根主要分布在530～560m及600～640m之间。将岩性、干酪根、孔隙度、流体饱和度数据引入所述方法中,在纵波速度的约束下计算球形孔隙与裂缝状孔隙的体积分数,进而预测横波速度。为了与测井习惯相符,将速度求倒数以慢度方式显示在图6中。由图6可见,作为约束的纵波慢度与实测慢度基本一致,其均方根误差和相关系数分别为1.8170和0.9613;而预测横波慢度与实测横波慢度趋势一致,大部分层段吻合较好,在部分层段(615～625m)预测效果略差,图中所示整段数据的均方根误差和相关系数分别为4.9340,0.8936,这个结果证明本文所构建的岩石物理横波速度预测方法能够在研究区目的层段获得较为准确的预测横波速度。对不吻合层段进行分析后认为预测速度效果不好的层段都是在脆性矿物(石英、方解石)含量较高的层段中出现高黏土含量薄层,在这种层段易发育裂缝,较高的裂缝密度使得这些层段速度特征更加复杂,且表现出强的各向异性,从而导致本文所提出的各向同性岩石物理横波速度预测方法的应用效果降低。

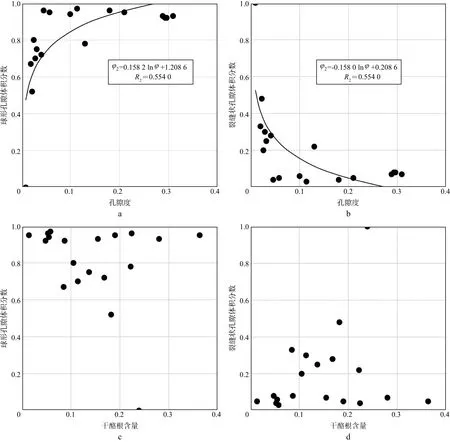
图5 利用实验室测试资料计算得到的球形孔隙与裂缝状孔隙体积分数与孔隙度、干酪根含量关系a 球形孔隙体积分数与孔隙度交会;b 裂缝状孔隙体积分数与孔隙度交会;c 球形孔隙体积分数与干酪根含量交会;d 裂缝状孔隙体积分数与干酪根含量交会

图7a和图7b是利用本文方法对实际测井数据计算的球形孔隙及裂缝状孔隙体积分数与孔隙度的交会图;图8a和图8b是计算的球形孔隙及裂缝状孔隙体积分数与干酪根含量的交会图。图7和图8与图5所展现的规律一致,即计算的球形孔隙和裂缝状孔隙体积分数与孔隙度呈对数关系,而球形孔隙和裂缝状孔隙体积分数与干酪根并无特别的关系。根据图5,图7所示的球形孔隙及裂缝状孔隙体积分数与孔隙度之间的关系,给出了利用孔隙度计算球形孔隙及裂缝状孔隙体积分数的公式(17)和公式(18),由此可以利用孔隙度计算球形孔隙及裂缝状孔隙体积分数,进而在不反演孔隙类型的情况下求取横波速度。

式中:φs和φc指球形和裂缝状孔隙体积分数;φ为孔隙度;a和b为常数。

图6 建南构造页岩气区域A井侏罗系东岳庙段富有机质泥页岩速度预测与实测数据对比(1ft≈0.3048m)

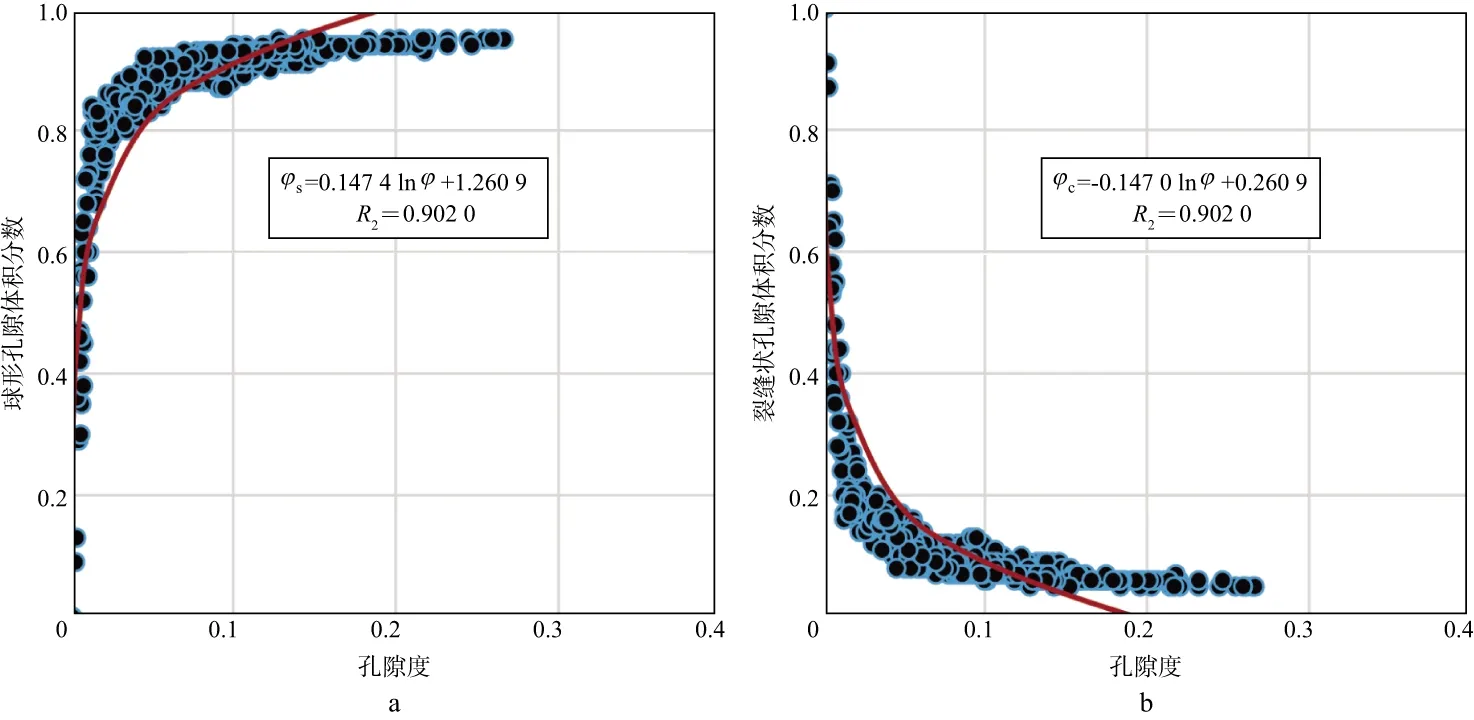
图7 利用实际测井资料计算得到的球形孔隙与裂缝状孔隙体积分数与孔隙度关系a 球形孔隙体积分数与孔隙度交会;b 裂缝状孔隙体积分数与孔隙度交会

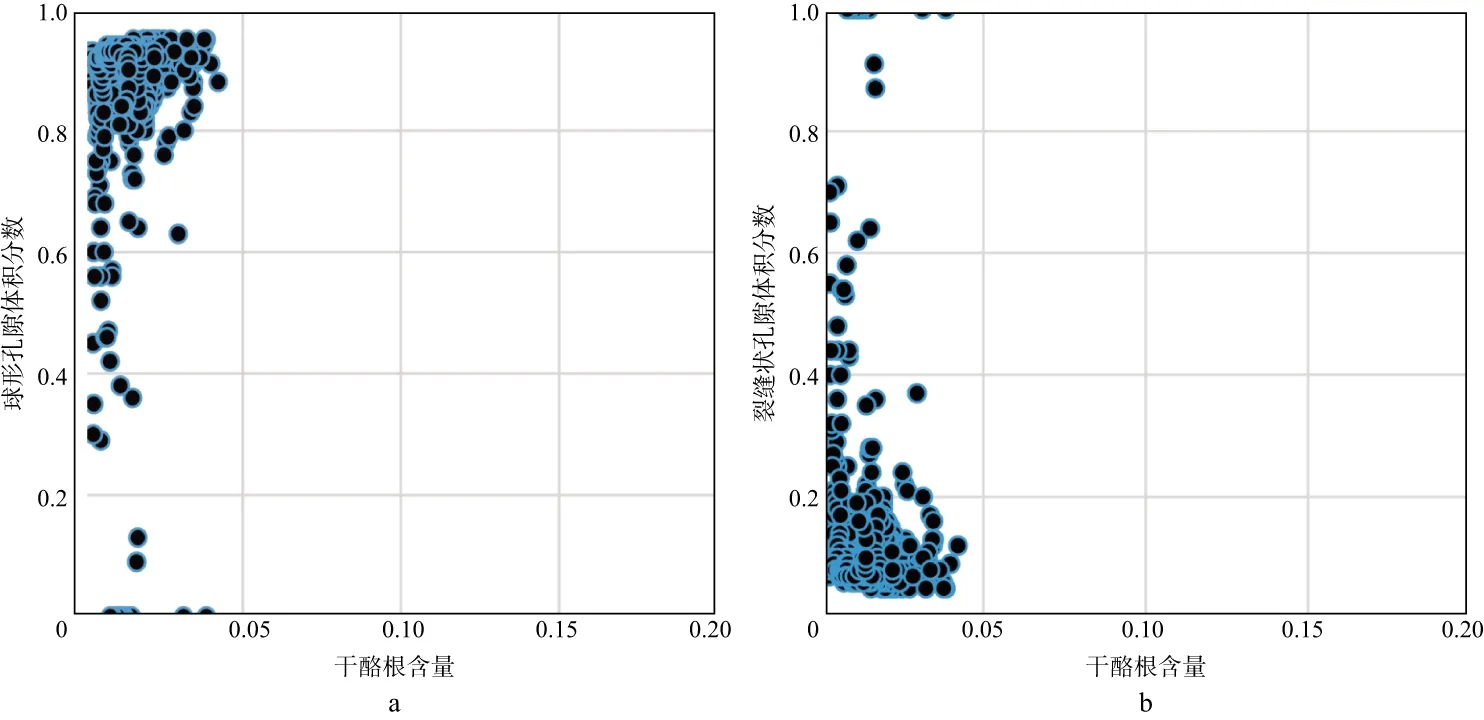
图8 利用实际测井资料计算得到的球形孔隙与裂缝状孔隙体积分数与干酪根含量关系a 球形孔隙体积分数与干酪根含量交会;b 裂缝状孔隙体积分数与干酪根含量交会

4 结束语

本文综合Keys-Xu岩石物理模型、Berryman的三维孔隙理论、Brown-Korringa固体替代技术、Gassmann流体替代技术等岩石物理理论和技术,提出了一种针对具有多矿物、复杂孔隙结构、含有机质的富有机质泥页岩岩石物理模型,在纵波速度约束下,利用该模型求取球形孔隙与裂缝状孔隙体积分数,再将所求的孔隙体积分数代入岩石物理模型预测横波速度。应用该方法对实验室测试资料及实际测井资料求取横波速度,结果显示,预测横波速度与实测横波速度较为吻合。19个样点的实验室测试资料和950个样点的井资料的相关系数分别为0.9439和0.8936,证明了本文所提出的横波速度预测方法在富有机质泥页岩横波速度预测中的有效性。