基于动态时间规整ICA算法地震随机噪声压制

逯宇佳,曹俊兴,田仁飞,吕雪松,何 沂

(成都理工大学地球物理学院,四川成都610059)

独立分量分析(ICA)是20世纪末出现的一种新型信号处理方法,该方法可在信源未知的条件下,仅依赖混合信号将混叠在一起的不同信号分离开来[1]。其基本思想是假设原始信号为相互独立的非高斯信号,利用信号的高阶统计量信息,提取观测信号独立分量成分,最终得到相互独立的源信号的近似估计[2-7]。1994年,COMON[8]首次提出了基于特征值分解的独立分量分析方法。1998年,CICHOCKI等[9]利用独立分量分析对含有加性噪声的混合信号进行解混,取得较好的效果。在地球物理领域中,ICA主要应用于地震数据去噪处理。2003年,刘喜武等[10]假设地震记录中有效信号和随机干扰在统计上独立且服从非高斯分布,对相邻两道地震记录进行ICA处理实现地震资料的去噪;LU等[11]提出基于独立分量分析的最大峰度自适应衰减算法实现了模型数据的多次波压制;2006年,MIRKO[12]将独立分量分析应用于P波和S波的波场分离;2011年,DONNO[13]将独立分量分析与最小二乘法相结合提出了改进的多次波消除算法;吕文彪等[14-16]先后利用改进的ICA算法对叠后数据、地震属性以及叠前数据进行了去噪处理;2012年,王维强等[17]将经验模态分解(EMD)技术与ICA技术结合应用于地震信号随机噪声压制;2016年,孙成禹等[18]通过构造度量数据非高斯性的目标函数,将地震数据转换到ICA域,结合阈值法实现了复杂地震资料的去噪处理。

传统的ICA算法如基于负熵的快速ICA算法只适用于地震同相轴较平缓的叠后数据,且算法不够稳定,容易出现解混失败现象,计算效率较低。针对这个问题,本文运用两步奇异值分解法对传统ICA算法的白化过程进行改进,将语音识别中的动态时间规整(DTW)与ICA算法相结合,利用动态时间规整进行地震道间的模式匹配,度量时间序列的相似程度,将地震数据的同相轴一一匹配,再利用ICA算法进行去噪处理。

1 方法原理

1.1 ICA算法

独立分量分析处理需要对观测信号矩阵进行去均值、预白化、ICA迭代处理。其中传统的白化过程需要利用类似于主成分分析(PCA)方法,如零时滞的协方差矩阵的特征值分解来完成。利用两步奇异值分解改进白化过程。

当观察信号个数(m)大于源的个数(n)时,ICA算法中白化过程可利用两步奇异值分解法(图像处理中又称AMUSE算法,即多个未知信号提取算法)[19]完成。这一过程能够实现源信号与噪声信号的分离。主要实现步骤如下。

1) 观测信号X减去它的均值,得到零均值观测信号,实现X的中心化。

2) 估计观测信号X的相关矩阵,即为协方差矩阵RX(0):

(1)

3) 利用奇异值分解(SVD)算法对RX(0)进行分解:

(2)

式中:VS为前n个特征值ΛS(从大到小排序)相对应的特征向量;VN为ΛN中后面m-n个不重要特征值ΛN=diag{λn+1,λn+2,…,λm}相对应的特征向量,λ为特征值。

5) 进行稳健的预白化变换:

(3)

(4)

(5)

(6)

经过以上两步奇异值分解,即可完成解混过程,避免了传统方法中复杂的迭代过程,在提高计算效率的同时也增加了算法的稳定性。

1.2 动态时间规整(DTW)

设时间序列X=(x1,x2,…,xn),Y=(y1,y2,…,yn),则X,Y的DTW距离[20-22]DDTW(xi,yj)定义为[23]:

(7)

式中:Dbase(xi,yj)表示向量点xi和yj之间的基距离,可以根据情况选择不同的距离度量。不失一般性,本文使用欧氏距离作为度量。根据公式(7),得到如图1所示的一个邻接矩阵,然后采用回溯法在邻接矩阵上对DDTW(xi,yj)值进行递归回溯搜索DTW弯曲路径。

图1 DTW弯曲路径示意

DTW距离允许序列点自我复制后再进行对齐匹配,能够很好地支持时间轴弯曲,并且它可以对非等长时间序列进行度量,也支持时间轴伸缩。DTW距离实际上就是确定序列X与Y上每个点之间的对齐匹配关系(点对匹配)。

弯曲路径必须满足以下3个基本条件[24]。

1) 边界条件:路径起始于点(x1,y1)、终止于点(xn,yn),它表示两个序列的起始点和结束点对应匹配。

2) 连续性:路径上的任意两个相邻点(xi1,yj1)和(xi2,yj2)满足条件0≤|i1-i2|≤1,0≤|j1-j2|≤1。

3) 单调性:若(xi1,yj1)和(xi2,yj2)为路径上前后两个点,则须满足i2-i1≥0,j2-j1≥0。

满足上述条件的弯曲路径有很多,每条弯曲路径都代表一种点对匹配关系。设弯曲路径为F=(f1,f2,…,fk,…,fK),fk=(i,j)k是弯曲路径上第k个元素,它表示xi和yj建立的匹配关系,路径长度满足max(n,m)≤K≤n+m-1。

点对匹配关系中,点对基距离之和的最小值即为DTW距离,对应的弯曲路径为最佳路径。DTW距离表示为:

(8)

求解最佳路径需要构造一个m行n列的累积距离矩阵Mm×n,矩阵中的每个元素γi,j定义为:

γi,j=Dbase(xi,yj)+min{γi-1,j,γi-1,j-1,γi,j-1}

(9)

γi,j为序列X[1∶i]与序列Y[1∶j]的DTW距离,因此,DDTW(X,Y)=γm,n,γm,n可以用动态时间规整法求解[25]。

1.3 基于动态时间规整的ICA算法实现步骤

基于动态时间规整的ICA算法去噪过程主要分为以下3个步骤:

1) 选取第1道地震记录作为模型道(模型道可以任选),利用动态时间规整算法对正演记录的同相轴进行特征匹配(具体实现过程如图1所示),在保证上覆水平层不变的情况下对下层倾斜地层同相轴进行校正拉平;

2) 利用两步奇异值分解法进行去噪处理;

3) 利用动态时间规整提取的道间时差将拉平且去噪后的地震数据还原为原始形态,完成整个去噪过程。

2 应用实例

2.1 模型测试

为了验证基于动态时间规整的ICA算法在地震随机噪声压制中的可行性,建立如图2a所示的速度模型,模型包含水平界面、倾斜界面、断层以及弯曲界面。通过正演模拟得到自激自收地震记录如图2b所示。在生成的正演记录中加入信噪比为0.5的高斯随机噪声见图3a。利用ICA算法直接(未使用DTW)对加噪数据进行去噪处理,图3b为去噪后的地震剖面,图3c为去除的噪声。由图3b可以看出,ICA算法在同相轴水平的位置去噪效果较好,而当同相轴倾斜或弯曲时,能够明显看到一部分有效波的信息被当成噪声去除了(图3c),有效信号损失严重,断层位置处尤为明显。

利用动态时间规整ICA算法对加噪数据进行去噪处理。图4a为动态时间规整特征匹配后的拉平剖面,图4b为两步奇异值分解法对拉平剖面的去噪结果,图5a为基于动态时间规整ICA算法去噪的结果剖面,与图3b对比可以看出,经过动态时间规整处理的去噪结果中随机噪声得到压制,且在复杂界面如断层、倾斜和弯曲界面的有效波信号保留较好,差剖面中没有残留有效信号(图5b)。

2.2 叠前去噪应用

高信噪比的地震数据是进行地震解释的重要基础。解释工作开始前,往往需要对叠前CRP道集数据进行层拉平或去噪处理,但这一工作非常费时,因此在保证去噪效果的同时,算法的计算效率显得尤为重要。为了验证两步奇异值分解法的实际效果,本文选用叠前CRP道集进行验证。叠前CRP道集是来自地下同一反射点的一系列地震响应特征,其每一道数据之间有极大的相似性,因此可利用ICA算法对其进行去噪处理。

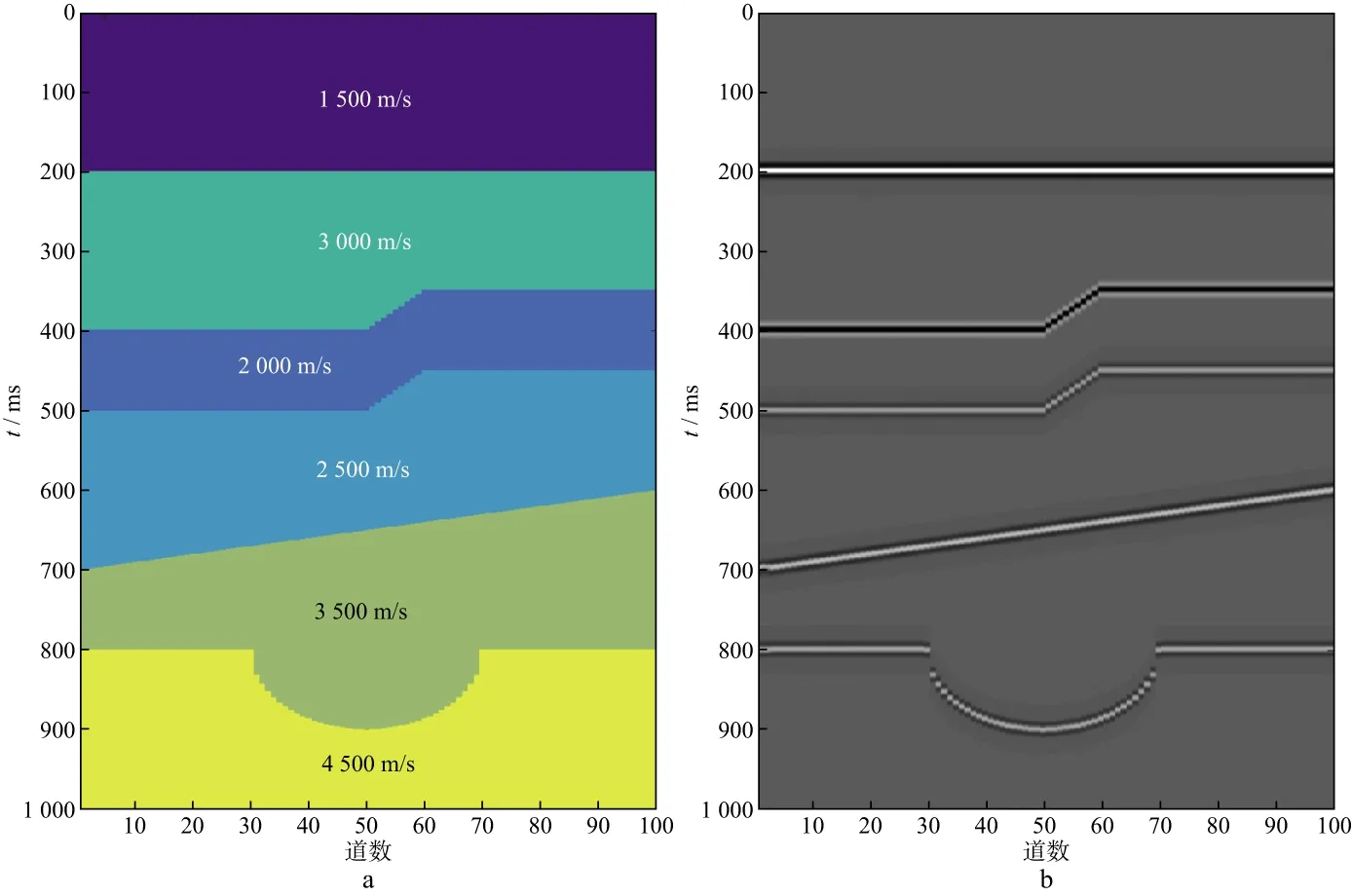
图2 速度模型(a)和正演记录(b)

图3 利用ICA算法处理的去噪效果(未使用DTW)a 加噪剖面;b 去噪后剖面;c 去除的噪声

去噪效果如图6所示。其中,图6a为原始CRP道集,图6b为基于负熵的快速ICA算法去噪结果,图6c为两步奇异值分解法的去噪剖面,图6d为两步奇异值分解法去除的噪声。相比于原始记录,两种去噪方法都能够有效去除原始剖面中的随机噪声,增强同相轴连续性。但是基于负熵的快速ICA算法处理结果中出现了由于迭代不收敛产生的坏道(图6b红色箭头处),破坏了原有的有效波信息。而两步奇异值分解法速度快,稳定性高,不需要复杂的迭代过程,可以直接对矩阵进行分解,最终得到的剖面同相轴连续,去噪效果有明显的改善。图7为图6 中叠前CRP数据对应的叠加剖面。对比图7a,图7b和图7c可以看出,利用两步奇异值分解法对叠前资料进行去噪处理后所得叠后剖面同相轴连续性增强(红色矩形框内较为明显),信噪比有所提高。

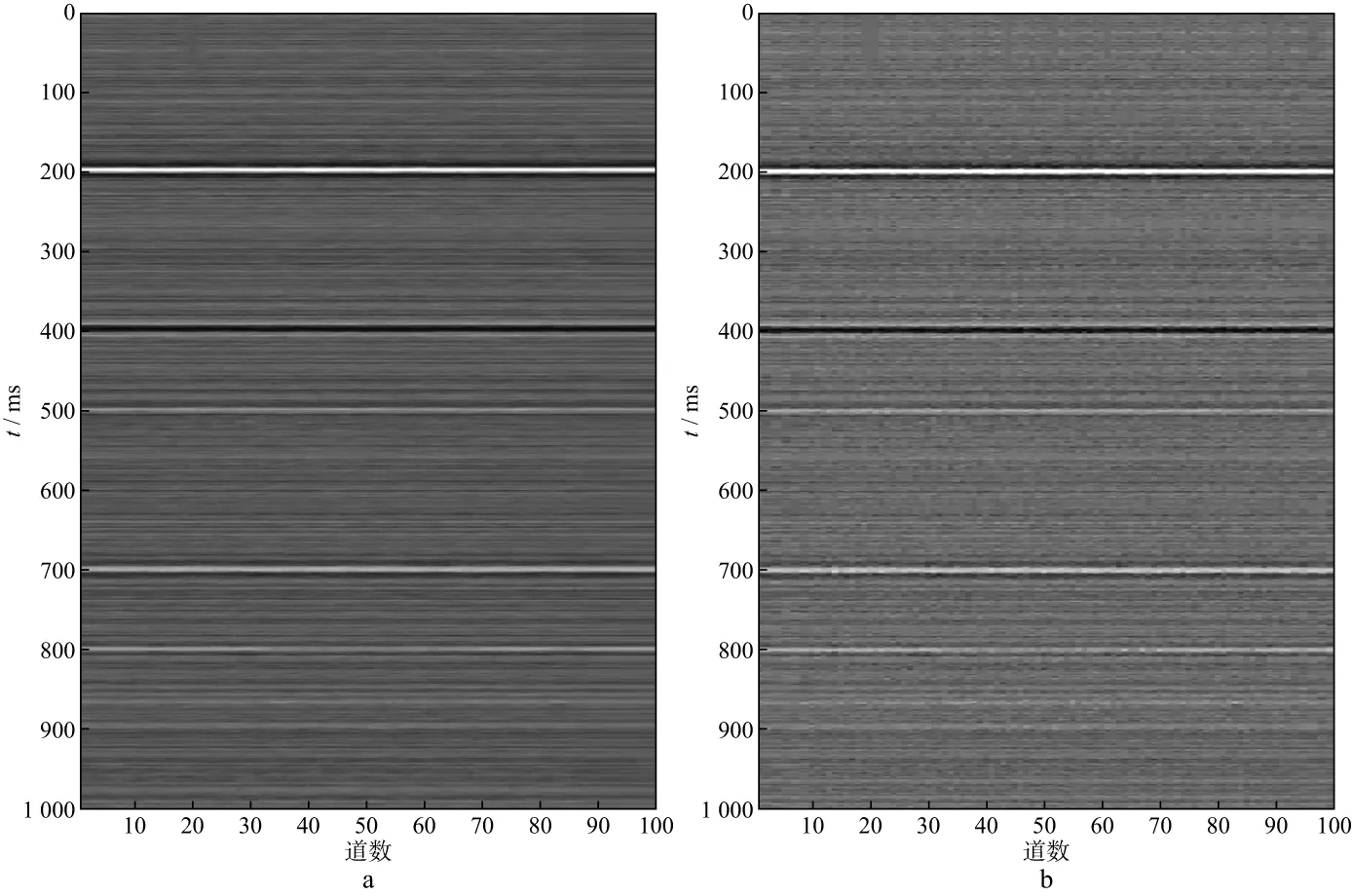
图4 基于动态时间规整ICA算法去噪效果(Ⅰ)a 动态时间规整特征匹配拉平剖面;b 两步奇异值分解法对拉平剖面去噪结果

图5 基于动态时间规整ICA算法的去噪效果(Ⅱ)a 基于动态时间规整还原后的去噪结果剖面;b 去除的噪声

2.3 叠后应用实例

将基于动态时间规整ICA算法应用于叠后地震资料随机噪声压制,结果如图8和图9所示。其中,图8a 是处理前的原始地震剖面;图8b是经过DTW处理后的层拉平剖面,由于原始地震资料的品质限制,中心位置拉平效果一般;图8c是拉平后两步奇异值算法去噪结果。图9b是基于负熵的快速ICA算法去噪结果,图9c是基于动态时间规整的ICA算法去噪结果。对比图9a,图9b和图9c可以看出,针对地层倾角较大且有断层存在的复杂剖面,基于负熵的快速ICA算法虽然能去除一部分的随机噪声,但是处理后的有效波同相轴能量变弱,连续性反而变差,这是因为在处理过中相邻地震道存在的时差使得地震道之间的相似性降低,从而导致算法不收敛产生坏道。采用基于动态时间规整的ICA算法去噪后,同相轴连续性明显增强,弱振幅信号得到放大,整体能量更为均一,断层信息更为突出,断点清晰可见(图9c红色椭圆标注)。图10对比了基于动态时间规整ICA算法去噪前、后的频谱,可以看出,本文方法去噪前、后频谱基本一致,未改变原始资料的频谱特征。相比于传统的方法,基于动态时间规整的ICA算法更适合复杂地震资料的随机噪声压制,有较好的实用价值。

图6 叠前CRP道集去噪效果a 原始记录;b 基于负熵的快速ICA算法去噪结果;c 两步奇异值分解法去噪结果;d 两步奇异值分解法去除的噪声

图9 叠后剖面去噪效果a 原始剖面;b 基于负熵的快速ICA算法去噪结果;c 基于动态时间规整ICA算法去噪结果;d 基于动态时间规整ICA算法去除的噪声

图10 基于动态时间规整ICA算法去噪前、后的频谱对比

3 结论

本文将ICA算法与动态时间规整相结合,提出了基于动态时间规整ICA算法,实现了叠前叠后数据的随机噪声压制处理,获得以下结论和认识:

1) 利用两步奇异值分解法对矩阵进行稳健白化,可将有效波和噪声分离。提高了ICA算法的稳定性和计算效率,随机噪声压制效果明显;

2) 将动态时间规整与ICA算法相结合,解决了仅利用ICA算法对非平缓同相轴的地震资料去噪不适应性问题;

3) 基于动态时间规整的ICA算法在实际资料应用中取得较好效果。既可以应用于叠前资料的随机噪声压制,也可以应用于叠后地震资料,具有普适性。