基于变权层次分析法的桥梁状态评估
胡铁明, 汪子龙, 韩基刚
(1. 沈阳大学 建筑工程学院, 辽宁 沈阳 110044;2. 辽宁省交通规划设计院有限责任公司, 辽宁 沈阳 110005)
近年来已建桥梁在运营过程中发生的特大安全事故屡见不鲜, 运营期桥梁的状态评估成为业主单位和管养部门关注的焦点. 桥梁状态评估是根据桥梁定期检查及桥梁长期监测结果, 运用科学的数据分析方法, 对现役桥梁状态(安全性、适用性、耐久性)进行评估[1]. 叶培伦等[2]结合混凝土桥梁结构特性构造了桥梁状态评价层次结构, 对评价指标进行了标准化计算, 建立了混凝土桥梁综合性能的评估模型; 张永清等[3]将层次分析法与多级模糊综合评判法相结合, 计算出各指标权重及隶属度, 根据评价得分确定桥梁状态等级.
基于层次分析法进行桥梁状态评估,是通过构造判断矩阵对定性问题进行定量分析,减少了决策者的主观影响,评价指标的选取更加灵活,具有整体性、灵活性、简洁性等优点.但其也存在一定缺陷,例如当某些指标所占权重小,而该指标存在很大缺陷,已经影响桥梁健康状态,却在总体评分体现不明显,缺陷被忽略,导致状态评估不真实.采用专家打分法确定挠度和应力评价指标权重过程中,不能根据桥梁结构特点合理分配指标截面或测点权重.
针对上述缺陷,引入变权综合理论,提出变权层次分析法,即采用先层次分析后变权综合的评估方法.同时在确定挠度与应力初始权重过程中,提出采用损伤敏感度法与极值差值比较法,使权重分配更符合桥梁自身结构特性,评估结果更真实、准确.
1 变权层次分析评价法
采用层次分析法将评估目标按支配关系分解成若干个层次,通过构建同一层次中指标重要性判断矩阵确定各评价指标的初始权重,根据桥梁长期监测结果与定期检查结果确定指标评价值,引入变权综合原理,从底层向上逐层进行变权综合,得到整体评价值.
1.1 判断矩阵一致性检验
对同一层次各评价指标进行重要性判断比较时,由于某些指标之间相互影响,且专家判断具有主观性,可能会出现“甲比乙重要,乙比丙重要,而丙又比甲重要”的错误判断.为避免这样的逻辑错误,计算初始权重前需要检验矩阵一致性.
第1步 计算矩阵一致性指标CI,
(1)
式中:λmax为判断矩阵的最大特征值;n为判断矩阵的维数.
CI值越大,一致性越差,当超过平均随机一致性指标RI时,认为指标重要性判断错误,需要对矩阵进行修正.
第2步 计算矩阵一致性比率CR,
(2)
CR值越小,矩阵一致性越好,通常认为当CR≤0.1时,一致性基本满足要求.否则,需要对判断矩阵进行修正,直到通过一致性检验[4].
1.2 底层指标评价值确定
根据长期监测和人工检测的结果类型,一般将底层评估指标分为3类.
第1类 没有具体的数值结果,只有对结构或构件状态的描述或等级的划分(如钢筋锈蚀程度、伸缩缝胶条损坏程度等),各等级中具体评分由专业检测人员根据实际情况酌情打分.
第2类 结果为具体数值.根据评价指标性质可分为正指标、负指标和适度指标3种类型.正指标数值越大越好,如混凝土强度、保护层厚度等;负指标数值越小越好,如混凝土氯离子含量、碳化深度等;适度指标存在最优值,指标数据越靠近最优值越好,如位移、应变等.对于不同指标,由于量纲不同无法直接进行打分,需进行无量纲化处理才能计算指标评价值.
第3类 结果为一数据序列(如梁体线性、主梁应力等).序列中各点的评价标准值并不相同,故需要考虑数据序列的均匀和不均匀变化,确定评估结果的步骤如下:
(1) 利用无量纲化法计算各测点的评价值.
(2) 采用各测点评价值与各测点权重相乘计算指标均匀变化的得分.
(3) 采用灰色关联度法计算非均匀变化系数.
(4) 计算指标评价值,其为指标均匀变化得分与不均匀变化系数的乘积.
1.3 变权均衡系数设定
变权的实质是根据指标自身状态和本组其他指标状态进行权重变动,达到各指标的状态均衡.决策者通过变权均衡系数来控制指标均衡状态,均衡系数α的取值在0~1之间,反映决策者对缺陷的容忍度.
假定某桥梁的上部、下部结构和桥面系的权重分别为0.6、0.3、0.1,上部结构与桥面系指标评价值均为90分,当下部结构出现缺陷时,整体评价值随均衡系数α取值变化,结果见图1.
从图1可以看出, 下部结构评价值越高, 均衡系数取值对总体评价值影响越小, 当下部结构存在明显缺陷时, 整体评价值随α取值的变化出现显著差异.α取值越大,表明决策者对缺陷的容忍度越大, 缺陷对整体评价值影响越小, 评价结果越接近于常权模式;α取值越小, 表明决策者越保守, 对缺陷越敏感. 查阅国内多个实际工程资料[5-7], 均衡系数α的取值一般在0.2~0.5之间.

图1 整体评价值与均衡系数关系
2 静态参量权重确定
静态参量中的挠度与应变是评定桥梁状态的关键指标.层次分析法中采用专家调查法或均分权重法确定挠度与应变指标权重,主观成分过大,且不能突出重点部位,故引入损伤敏感度法和极值差值比较法(储备值法)确定挠度、应变截面和测点权重(同一挠度监测截面上各测点,可以认为其权重相等).
2.1 损伤敏感度法
采用降低有限元分析模型中的整体刚度的方法来模拟结构损伤,通过各截面或测点响应量的变化程度计算损伤敏感度因子Si,归一化处理后得到初始权重.
(3)
式中:μi为敏感度矩阵中第i行元素绝对值的平均值,即发生结构损伤时,i截面或测点响应变化量的平均值;σi为敏感度矩阵中第i行元素的标准差;n为截面数.
对于简支或跨数较少的桥梁,局部损伤会造成全桥性响应,而对于多跨结构的大型桥梁,全桥性响应量可能无法体现局部损伤.为保证权重计算准确,应根据结构特性将多跨结构分为多个部分,再计算损伤敏感度因子.
损伤敏感度因子越大,说明该截面或测点响应量的变化越能明显反映结构损伤,故在评估中所占权重应越大.
2.2 极值差值比较法
极值差值比较法,又称储备值法.通过计算各截面或测点储备值来反映该响应量的变化对结构状态的影响程度,储备值越大,说明安全系数越大,故权重应越小.将各截面或测点的储备值两两相比,构成判断矩阵,判断该矩阵的一致性,并计算权重.
计算应变监测截面与测点权重时, 利用混凝土梁桥同一构件内各截面的极限抗压强度和抗拉强度设计值相同的特点, 选取材料设计极限值与设计规范中最不利载荷工况下极限值差值的最小绝对值作为强度储备值; 计算挠度监测截面权重时, 将规范中挠度极限值与设计规范中最不利载荷工况下挠度值的差值绝对值作为挠度储备值.
3 工程应用
以辽宁省某混凝土梁桥(上行方向)为工程依托,对主桥上部结构进行状态评估.主桥(第38~40孔)上部结构为变截面连续箱梁,支座采用GPZ系列盆式橡胶支座,桥面连续,日平均交通量为9 613辆,设计载荷等级为汽车-超20、挂车-120.
2017年7月辽宁省交通规划设计院对主桥进行了载荷试验和人工定期检查.载荷试验结果表明:各孔正弯矩截面底板应变校验系数与挠度校验系数均在规范常值之内,但各孔截面都存在个别应变校验系数超过规范常值,说明混凝土强度满足设计要求,但材料老化,强度降低;相对应变残差与相对残余变形均在规范限值(20%)之内,说明结构处于弹性状态.人工定期检查结果为2类技术状况.
3.1 层次分析
健康监测系统对主桥跨中挠度、跨中下缘混凝土应变以及自振频率进行实时监测,运营状态良好.以桥梁健康监测数据与人工定期检查结果为评价依据,采用层次分析法建立主梁状态评估模型,如图2所示.

图2 主梁状态评估模型Fig.2 The evaluation model of girder state
矩阵评定标度选用1~9矩阵标度法,数字越大,表明某指标对另一指标越重要(1表示两指标同等重要),若某指标比另一指标次要,则用倒数表示;数值越小,表明该指标相比另一指标重要性越低.
根据4名专家的打分结果构造判断矩阵,进行一致性判断,并求得指标权重向量.假设这4名专家水平相同,采用群组决策中加权几何平均综合排序向量法计算权重wj,计算结果见表1.

表1 指标权重Table 1 The weight of index

(4)
式中,wj1为第1名专家对第j个指标计算权重,以此类推;n为指标总数;s为专家人数.
3.2 挠度与应变截面权重
采用极值差值比较法确定各截面挠度与应变初始权重.主桥上部结构采用有限元软件MIDAS Civil建立空间模型,选择空间梁系单元模拟实桥结构[8],共121个节点,120个单元,见图3.

图3 主梁有限元模型Fig.3 The finite element model of girder
以挠度为例,将有限元模拟设计最不利工况下跨中挠度作为理论最大值,表2为各截面极值差值,根据各截面极值差两两对比,构造挠度截面权重判断矩阵(见表3).求得矩阵特征向量,即为截面初始权重:0.38、0.25、0.37.
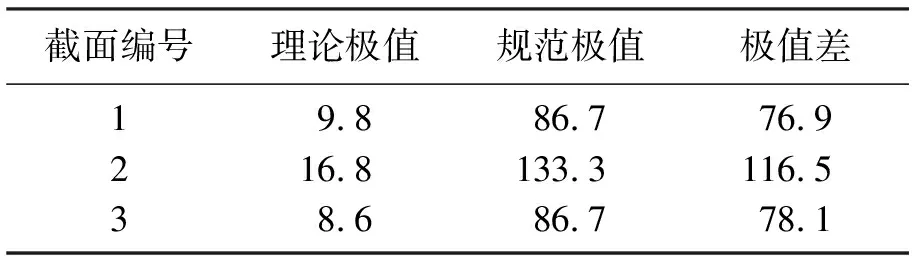
表2 各截面挠度极值差
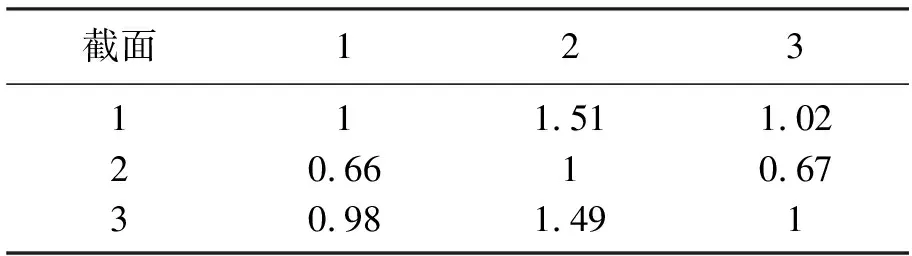
表3 截面权重判断矩阵表Table 3 The judgment matrix of section weight
同理,以混凝土材料抗拉强度值与有限元模拟截面最大拉应变为规范极值与理论极值,求得各应变截面权重为0.33、0.4、0.27.
3.3 指标评价值确定
采用适度指标无量纲化模型式(5)计算挠度、自振频率指标权重.挠度指标最优值为0,以有限元模拟中结构最大上拱值和下挠值为评估范围的最大、最小值;自振频率指标以有限元模拟计算值为最优值,最大、最小值为最优值上下浮动10%.
适度指标无量纲化模型:
式中:X为评估指标数值;Xn、Xm、X0分别为评估指标区域范围内的最小值、最大值和最优值;A为评估值的最高值;B为指标数值与指标评价值之间的相互关系,B=0表示其为线性关系.
本系统应变监测值是以传感器安装时混凝土应变为初值,若直接采用应变监测值与有限元模拟值进行比较存在不妥之处.故选择可变载荷产生的应变增量为评价依据,根据文献[9]与桥梁长期监测数据,确定温度与应变为线性强相关,采用线性回归法剔除应变中温度效应作用,最终得到可变载荷作用应变值.以1 h内可变载荷产生的最大拉应变为应变指标数值,以载荷试验时该截面最不利工况下应变监测增量为最大值,最小值为0,采用负指标无量纲化模型式(6)计算评价值.
负指标无量纲化模型:
(6)
跨中挠度、自振频率与混凝土应变指标的实测数值与评估区域见表4.

表4 指标实测值与评估区域Table 4 The measured value and the evaluation area
混凝土强度指标评价值采用正指标无量纲化模型式(7)计算,以各测区平均强度值为指标数值,混凝土强度标准值为最大值,最小值为0.
正指标无量纲化模型:
(7)
采用分等级打分确定结构外观指标评价值,根据《公路桥梁承载能力检测评定规程》(JTG/TJ21—2011)和《公路养护技术规范》(JTG H10—2009),将各指标评价分为5级,根据等级确定其评估值范围,1级:100~80分;2级:80~60分;3级:60~40分;4级:40~20分;5级:20~0分,具体分值由专业检测人员酌情确定.指标评价值计算结果见表5.
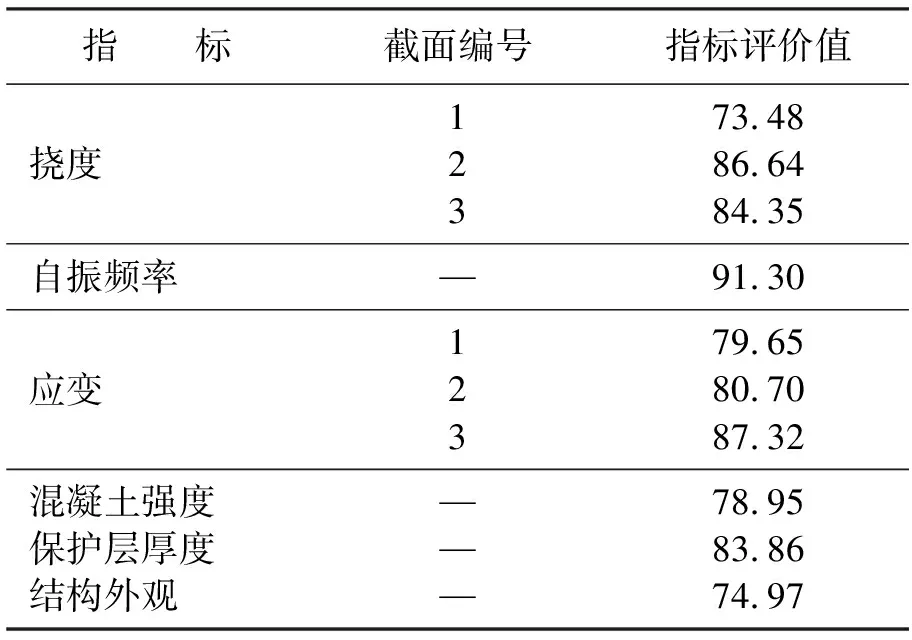
表5 指标评价值Table 5 The estimate evaluation of index
3.4 变权综合评价
根据指标评价值对同层次中评价指标进行变权处理,见式(8),均衡系数α取0.2.
(8)

对挠度与应变指标截面层进行变权计算,挠度各截面变权后权重分别为0.41、0.24、0.35,评价值为80.44;应变各截面变权后权重分别为0.34、0.41、0.25,评价值为81.00分.
按上述步骤从底层逐层向上进行变权综合,最终主梁整体评价值为81.01分,根据《公路桥梁技术状况评定标准》(JTG/T H21—2011)判定主梁为2类技术状况,与载荷试验评定和人工定期检查结论相符.
4 结 语
(1) 层次分析法通过将桥梁结构状态评估分解为合理有序的递阶层次结构,构造判断矩阵,将各指标重要程度的定性问题定量化,很大程度上减少了主观因素的影响,并能够根据已有检测与监测指标结果灵活选取评价指标,使评估工作更加科学有效.
(2) 采用损伤敏感度法和极值差值法确定挠度与应变指标初始权重,能够考虑不同桥梁结构特点,使权重计算结果更科学可靠.
(3) 对各指标初始权重进行变权处理时,均衡系数α的取值反映决策者对缺陷的容忍程度,对于运营期桥梁状态评估工作,建议取值在0.2~0.5之间.
(4) 将层次分析法与变权综合评价法相结合,能够弥补层次分析法中对短板效应考虑不足的缺陷,使评估结果更接近于桥梁的真实状态,在未来的桥梁状态评估工作中有很好的发展及应用前景.

