基于图编码的网络拓扑语义挖掘*

杨 扬，张 驰

（中国科学技术大学 电子工程与信息科学系 中国科学院电磁空间信息重点实验室，安徽 合肥 230027）

0 引 言

信息产业的高速发展，使得互联网逐渐深入人们的生产生活。在线的社交逐渐成为人们交流信息、交换利益和建立社会关系的重要方式。同时，这些社交的关系数据事实上蕴含了现实中对象的大量信息。通过对各种各样社交网络中的关系数据进行挖掘，可以发掘出网络中对象的社交圈、行为模式和社会角色。通常，实际中的网络出于隐私保护的需求，其节点和边都经过匿名化的处理。因此，对于网络拓扑结构数据的研究是挖掘网络信息一个重要手段[1]。

在当今数据时代，数据量和信息量爆炸，所面对的网络数据也极为巨大。面对纷繁复杂的网络结构数据，从中挖掘出有用的信息也有极大的理论和实际意义。因此，需要将大规模的网络数据进行简化和去冗余，提取图中的语义信息，为进一步研究、理论分析和应用提供基础和帮助。

1 基本概念、研究现状及问题

1.1 图、子结构和结构语义

用一个二元组G=(V,E)来表示图或者网络，其中V和E分别表示图中的点集合边集，对应网络中的对象集合和它们之间的关系集合。两个点u、v之间有关系，如果它们之间存在一条边e={u,v}相连。仅研究网络的拓扑结构而不考虑其所具有的标签和权值，这在现实中可以对应匿名的社交网络，或者其他一切无标签或者去标签的网络。

通常来说，图中的某些子图或子结构具有显著的特征，这个“特征”可以是多种多样的，如稠密性特征可以对应到派系（Clique），相似性特征可以反映到二部图（Bipartite）上，相对稠密度则可以定义社区或社团（Community）的概念。子结构和子图指的是同一个对象，只不过在强调子图的结构方面时也称子图为子结构。

在社交网络或者更多网络中，子结构包含了图中点的一些语义信息，这是由于不同的结构类型具有不同的意义，蕴含了不同的连接模式信息。此外，局部的子结构通过一些重叠关系组合而成整体的网络[2-3]。它们之间的这种重叠关系也反映了网络从局部结构到整体之间的关系，也是网络拓扑信息的一部分。可以说，网络的子图特征和组合方式是网络结构数据的拓扑语义。

一直以来，社交网络的主要结构被认为是社团或者簇（Cluster）。对于社团的挖掘算法，是基于对社团的不同理解和定义[4]。然而，对于社团的进一步结构语义并没有更多挖掘。事实上，社团也是一种特殊的子结构，即内部连接相对外部更紧密的结构。按照这种稠密性定义，社团的语义是指具有较多相互联系团体。当然，社团也有不同的定义，但认为社团是一个基于某种相似目标或者共性而连接较为紧密的团体。通过这种语义，社团内部的点是无法区分的。

事实上，图中的子结构并不仅限于社团，图中的稀疏结构仍然具有一定的意义。典型的星（Star）结构是一个稀疏的子图。它的语义是指一对多的一种团体关系。在团体内部，枢纽点（Hub-node）是这个子图的中心或者领头，信息通常通过这个点发布最快，而剩余的辐点（Spokes）是这个子图的信息接收点或者采集点。派系是聚集的朋友圈的代表，其语义是具有两两社交关系的团体，在团体内部的点与其他点都具有关系，也是一种特殊的社团。通常的派系并不见得完美，即会存在一些派系中的点与其他点之间没有直接的连接关系。但是，这不妨碍它成为一个紧密联系的团体，称为近派系。其他的稀疏子图如树（Tree）和链（Chain），则分别刻画了一种层次的上下级连接关系和前后相继的传递关系语义。二部图则表明两个相对的团体，团体内部是具有相似邻居集合的点集。由于在现实中的网络中较为常见，将这5种子图（如图1所示）以及近派系作为基本的语义模板（Template）。由于后面将通过这个模板来编码子图，也称它为字典模板。

图1 基本的语义模板

图的拓扑结构语义不仅包括子图的类型或者说子图的局部结构语义，还包括子图之间的关系。子图之间的关系最重要的是重叠关系。当两个子图共享一个点时，表明这个公共点可能存在两个不同的身份或角色，亦或是连接两个团体的中间人。当两个子图存在重叠边时，表明这个连接关系对应的两个点已经同时隶属两个团体，且它们在不同的团体中同时存在关系。子图重叠程度的判断，是一个困难的问题，需要从图的实际情况出发，挖掘出其所具有的真实结构。

1.2 研究现状与问题

现有的社区发现算法、图分解算法和图聚类算法，是解构网络拓扑结构的有效手段之一。常用的社区发现算法虽然基于稠密度[5]、相似度[6]和模块度[7]特征得到了一些不同语义的社区，但是网络中的结构多样，不限于社区。为此，存在很多专门挖掘网络中局部子图的方法[8-9]，但其总是针对具体的单一子结构，有的挖掘算法具有较高的复杂度，且每种子结构的挖掘标准不同。Navlakha等人[10]首次将信息论中的最小描述长度（Minimum Description Length，MDL）准则[11]作为统一的标准来评判结构挖掘算法的优劣，然而仅涉及了网络中的二部图结构。之后，Koutra等人[12]结合最小描述长度准则提出了Vog的网络的拓扑语义理解框架，将多种子结构采用统一的方法进行挖掘，但忽略了稀疏的子结构，同时并没有很好地处理对于子图间的重叠语义。

图分解问题。大规模的图首先需要分解成合适的子图，再进一步提取它们的语义。Vog的框架的表现优劣仍然取决于分法的好坏，所用的Slashburn分解算法甚至不能解决简单的分解重叠问题。如图2所示，Slashburn不能鉴别出明显的重叠边，而是将它作为一个星形子结构的一条边（1），但事实上a是两个星的重叠边（3）。另外，Slashburn通过枢纽点挖掘，完全忽略了这个大的子结构（2）中的一个派系结构（4）。为此，通过直接挖取图中枢纽点并进行子结构合并，得到了图的子图集合。

图2 Slashburn忽略了子图重叠

子图的语义判别问题。子图的语义判别需要合理的语义模板和编码算法。为此，引入多样化的子结构模板，包含稠密和稀疏的各种子结构，通过合适的编码方式，结合MDL，快速确定子图语义。

子图重叠问题。子图的重叠程度判定问题一直是一个困难的问题。通过从每个枢纽点的自网络（Ego-net）出发，利用MDL来确定重叠的子图是否应该合并，然后逐步迭代，直到确定图的所有子结构的重叠语义。

2 网络结构语义挖掘方法

网络由许多子结构构成。为挖掘图所蕴含的结构语义，总体思路如下。

第一步，鉴于Slashburn分解算法忽略一些重叠语义，通过基于枢纽点的聚合方法（Hub-based subgraph Mining，HM算法）保留图的重叠语义，得到待识别语义的子图集合D。这些枢纽点的自网络，可以通过MDL编码识别为星、派系和近派系等直径不超过2的子图。一个点的自网络，是指这个点的所有邻居点以及它本身作成的子图。由于还要形成直径较大的子图，再通过进一步合并形成潜在的树、二部图或者链这些长直径子图，而具体的子结构类型判断参照第二步。合并结束，子图间的重叠语义已经被确定。

第二步，对D中的每一个子图，通过MDL来确定子图的结构语义。在确定子图语义时，采用基本的字典语义模板，因此称为基于模板的图语义挖掘（Template-based graph Semantic Mining，TSM）算法（如图3所示）。

第三步，希望得到原图的一个模板表示，但显然这么大的图并没有一个模板是合适的。因此，通过将原图分解得到子图集合对应的语义模板集合进行组合选择。根据MDL准则，可以得到最佳的模板集合，作为对图的整体语义的一个理解。

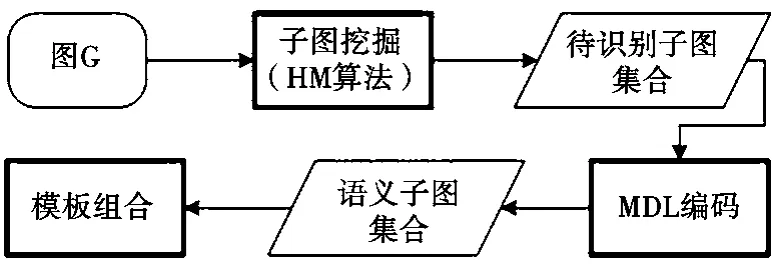
图3 TSM算法流程

2.1 HM算法

HM算法流程如下。

输入：图G

输出：子图集合D

1:对每个2-degree点的邻居点和两条边作成的子图V2(x)进行合并，得到子图

2:取H的每个连通分支，添加到D2

3:对degree＞2的每个点，取其自网络，去掉重复一样的子图，得到子图集合D1={S1,S2,…,Sp}.

4:D1=shm(D1)#shm()是一个递归函数

5:return D=D1∪D2

6:def shm(D1):

7: while True：

8: if |D1|==1:

9: return D1

10: else:

11: if D1不存在真包含关系的子图：

12： if P(D1)不存在正项：

13: return D1

14: D1=f(D1)

15: elseif D1存在真包含关系的子图：

16: 选择最小真包含子图集合U0={S1,S2,…,St}以及其母图S*

17: U=shm(U0)

18: U1=g(U,S*)

19: D1=(D1-(U0∪ S*))∪ U1

20: #f(A)和g(B,C)分别表示将子图集合A进行一次合并处理、将B和C进行一次真包含处理。

首先，需要得到图的子图。大部分现实中的网络都服从幂率分布[13-14]，即存在少数度相对较大的枢纽点。J.Leskovec等人[15]的研究表明，枢纽点将网络中的一个个子结构连接起来，使得传统的图分割算法难以奏效。因此，枢纽点的结构是一种图的结构语义。在难以判断该结构的具体类型时，直接挖掘派系和星形模板的短直径共性，将所有度大于2的点包含它的自网络挖掘出来，作为第一步的初始子图集合D1。而度为2的点只有3种情形（见图4），要么是一条链的节点（1），要么已经被某个度大于2的枢纽点通过自网络包括进来（2），要么就是一个独立连通的三角形中的一个点（3）。（2）的情况已经在前面处理，因此对每个度为2的点x，它的两条边以及两个邻居点组成一个子图。将所有这些子图合并（合并是指合并后的点集是子图的点集之并，边集是子图的边集之并；并不是合并后的点集的导出子图，因为通过后面的取法知道，边一定会被收入到某个自网络之中，并不会遗漏需要编码的边而产生很多误差），重复的边只计数一次，得到一个大的图，记为H，通常具有多个连通分支。取H的所有连通子图，将它们作为待识别的语义子图添加到候选集D2中。最后，度为1的点显然都已经存在于D=D1∪D2的子图中。

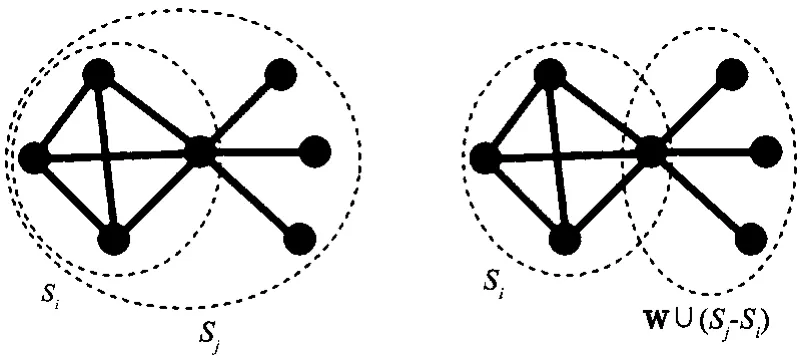
图4 真包含关系子图的合并

尽管这里D1是记为一个集合，但事实上通过前面的添加方式会有很多重复的子图，因此需要去掉一样的子图。不妨，记去重后的子图集合仍为D1。由于D2中的子图倾向于链结构，因此它们的语义类似于将D1中的子图串起来。所以，仅仅合并D1中的子图，以便形成语义明显的大型结构。

任取两个子图S1,S2∈D1，记T=S1∪S2，K=S1∩S2，考虑S1，S2的合并。两个子图间的关系有真包含、不相交和“通常重叠”三种。“通常重叠”是指不是真包含关系的重叠。先研究两个子图间的真包含和“通常重叠”关系处理，对于实际子图合并的情况在后面讨论，而不相交的子图显然不考虑合并问题。

两个子图间真包含关系表明了一种层次语义，合并时的处理与一般的重叠不同，要另外处理。设Si真包含于Sj，考虑两种情形，一种是将图看作成一个子图Sj，另一种是看成Si和W∪(Sj-Si)多个子图重叠在一起，其中即与Sj-Si中有边相连的点的全体。通过计算两种情形的子图集合编码，并由MDL准则选择编码长度最小的一种。注意，W∪(Sj-Si)有可能是具有多个连通分支的子图集合，这时把每个连通分支作为一个子图，然后对每个子图用字典模板编码，最后将这些字典模板合起来（根据式（1）和式（2））对整个图进行编码，这个过程称为一次“真包含处理”。

通常，最小描述长度准则是指通过子结构或者子结构集合M来描述图数据G。编码所需的比特数目越小，意味着对图数据的压缩越好，也就是对数据的理解越好，是更好的编码。通常，编码分为两个部分，子结构集合的编码和误差的编码，即无损压缩：

其中L(M)和L(G|M)分别是对子结构集合的编码比特和对误差的编码比特数目，且有：

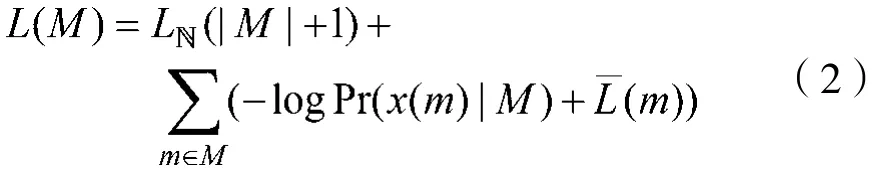
对于剩余的重叠情况，即“通常重叠”情况，有两个问题：（1）两个子图合并的条件是什么？（2）这么多子图的合并顺序是怎样？计算每两个子图间的合并编码收益，记号同前；设G(T)为T在G中的导出子图，则定义Si、Sj的合并编码收益为：

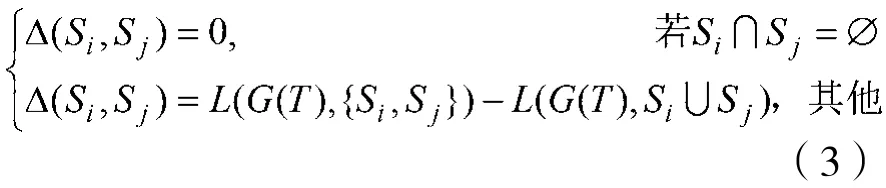
即合并前的编码比特数减去合并后的编码比特数。若差值大于0，则合并减少了局部的编码比特。由MDL知，合并是有益的，则将两个子图合并；否则不合并。对于以上处理，称为一次“合并处理”。

对于第二个问题，设k=|D1|，则任意两个子图计算编码收益可以得到编码收益矩阵P=(∆(Si,Sj))k×k。在合并迭代的每一步，选择P中最大正数对应的两个子图合并，同时对合并后的子图更新它与其他子图的合并收益，然后重复迭代，直到P中不再出现正项。此时，D1是动态变化的，但是仍记为D1。

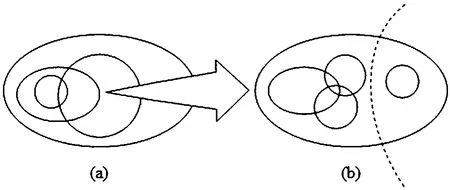
图5 子图间的一般关系

事实上，真包含的关系并不简单（图5），即可能存在一个子图真包含一个子图再真包含着一个子图的多层真包含关系（图5（a）），也存在一个子图包含多个非真包含关系的子图（图5（b））。重叠也有多个子图两两重叠的情形。一般地，从最小的子图开始（即考虑图5例子（a）中的最小真包含子图部分（b）），即设一系列子图U0={S1,S2,…,St}是子图S*的所有真包含子图，而Si，i=1,2,…,t不再真包含D1中的其他子图。于是，Si、Sj之间的关系仅有不相交或“通常重叠”两种。用前面同样的办法处理“通常重叠”，结束后得到一系列不能再合并的子图集合 U={S´1,S´2,…,S´g}。最后，对U中的每个子图S，通过两个真包含子图的类似处理，计算它与S*之间的真包含关系比特，即解优化问题：

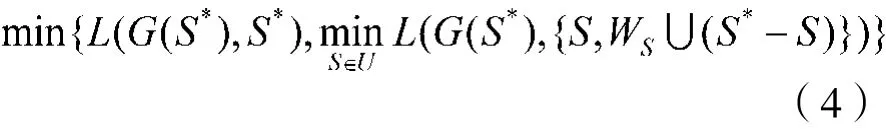
然后，将以上对于子图集合D1的合并迭代逐步进行，直到图中不再有真包含的子图，同时子图间的合并收益矩阵P不再有正项。整个子图合并算法结束后，得到一个待识别语义的子图集合D=D1∪D2，其中的子图可以是重叠的。

2.2 子图语义判别方法

对于子图集合D，需要判别每个子图的具体子结构类型，即提取图的拓扑语义。子图的拓扑语义或者说子结构类型是基本字典中的某个模板类型。

通过最小描述长度准则，将子图g∈D的子结构类型判别问题公式化：

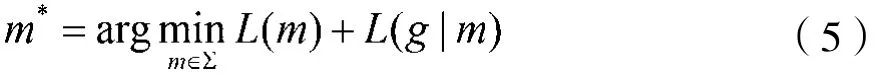
其中∑是六种基本模板所组成的字典，包括星（st）、派系（cl）、近派系（nc）、二部图（bp）、链（ch）和树（tr）。无歧义地，记∑={st,cl,nc,bp,ch,tr}；L(m)和L(g|m)分别是对模板m和模板与子图间误差的编码。

显然，这个算法的关键取决于模板和误差的编码两部分。通过最优前缀码对模板进行编码。总体而言，总是编码模板的大小，然后确定模板中每个点对应在子图中的位置。模板的编码公式如下。

（1）派系（Clique，cl）

（2）近派系（Near Clique，nc）

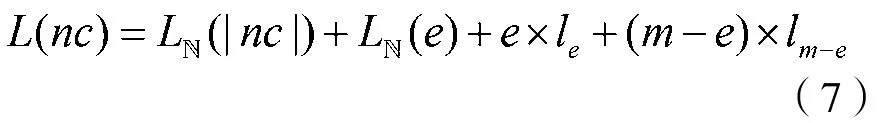
（3）星（Star，st）

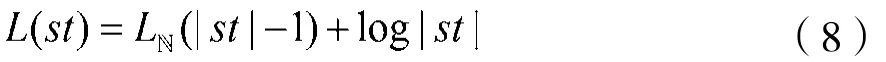
（4）二部图（Bipartite graph，bp）：

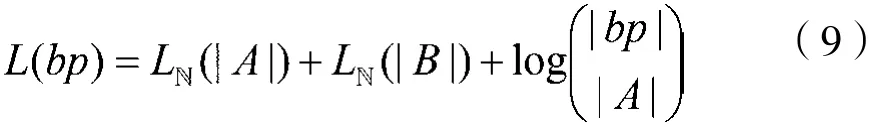
（5）树 (Tree，tr)：

（6）链（Chain，ch）：

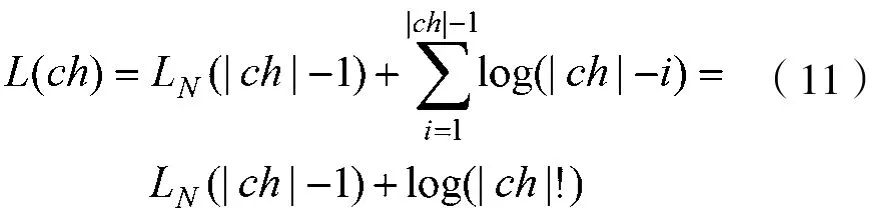
对于误差的编码，首先通过模板m与子图g对应的邻接矩阵作异或和计算得到误差矩阵e，然后将误差矩阵e分为两个部分e=e++e-，分别表示模板有而图不具有的边、图具有而模板不具有的边。因为它们的分布是不同的，所以需要把它们分开来编码。编码公式如下：

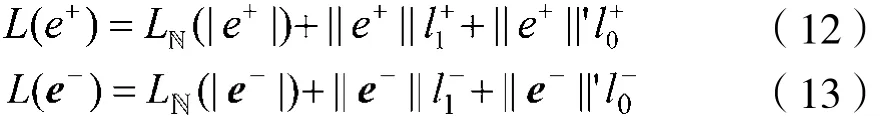
这也相当于在矩阵e+或e-中编码它的上三角部分，可以看做是按行编码，即将它逐行作为一个0-1比特串来编码。|e+|是矩阵e+对应的图中不重复边的数目，也就是e+上三角部分中1的数目；||e+||和||e+||´分别表示上三角部分中1和0的数目；而

是每个比特最优前缀码的码长。e-的编码类似。最后，由于并不是单纯地编码比特串而是矩阵，因此需要再加上对矩阵阶数的编码。于是，最终的误差编码长度为：

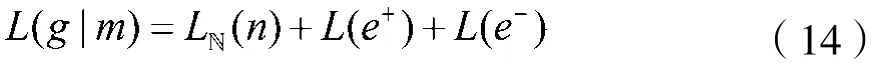
这样，即可自动计算出G中每个子图的g的结构语义模板类型。对于得到编码后的模板集合，记为 O={m1,m2,…,mk}。

2.3 子图组合算法

从前面的两个步骤已经确定了图的子图语义和子图间的重叠语义，但是整体而言，图G也需要一个简洁的模板表示。也就是说，需要把这些子图对应的语义模板放在一起，组合成原图的一个整体语义，通过MDL来确定这个模板集合中模板之间的语义，即应该选择哪些模板得到整体的拓扑语义。通常，对于确定的模板集合O，其解空间的遍历也需要O(k2)的时间复杂度，其中k=|O|是子结构的数量。当子结构数量较多时，这并不是好的选择。为此，采用2种模板选择近似算法。这两种模板选择算法结合TSM算法，称之为TSM-AA和TSM-GA算法，完全对应于Vog中的PLAIN和GREEDY’N FORGET组合方法。选择模板组合时，当两个模板重叠时，对于重叠边采用逻辑加，即重复出现的边只计算一次。与Vog不同的是，认为模板的顺序并不重要，重复的惩罚因子隐含在模板数量和模板的编码中。

3 实验对比与分析

实验采用了几个社交网络和文献引用网络，分别是Citnet[16]（文献引用网络）、Euall[17]（文献引用网络）、Enron[18]（邮件往来网络）和Facebook[19]（社交网络）。对这四个数据集采用TSM-AA和TSM-GA算法，计算每种组合用来编码原图所需的比特。由MDL准则可知，比特数越少，表明该子图集合越好。然而，由于MDL倾向于惩罚重叠的部分，因此会尽量选择不重叠的模板。所以，TSM算法得到的结果不见得比Vog好。这四个网络的基本数据见表1。

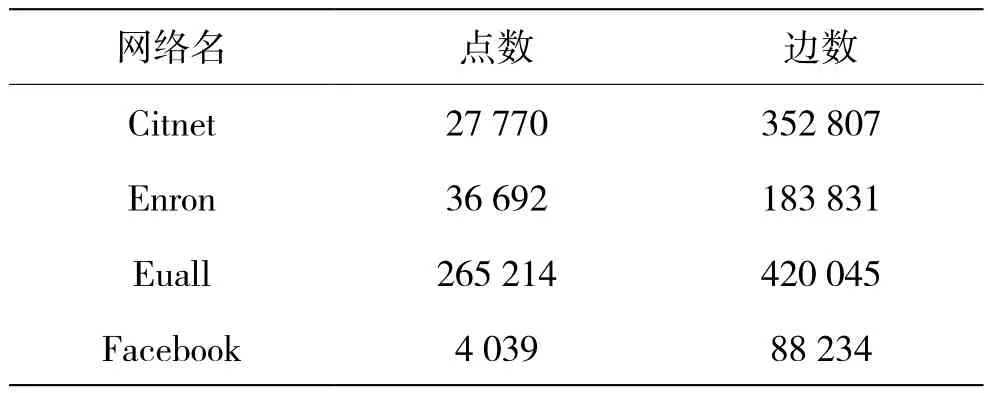
表1 图数据概况

首先比较三种算法，将图编码成纯误差。TSM-AA，即将分解得到模板集合全体作为整体的图编码模板；TSM-GA，即根据局部收益进行贪婪算法选择最终的模板集合。由实验结果（如表2所示），TSM-AA算法由于大量的冗余，用它编码图所需的比特远超其他两种算法；TSM-GA编码图仅需更少的比特数目。根据MDL准则，它是对图结构的较好理解。

然后，通过计算Vog算法在图数据上的比特进行比较发现，同是贪婪算法，尽管可能存在更多的子结构重叠，但所提算法计算得到的编码比特数目更少，表明是对图语义结构的更好理解和算法改进，如表3所示。

表2 三种算法编码图所需的总比特

表3 与Vog的算法比较

总之，相比于Vog算法，所提算法能够挖掘出图中更多的子图重叠语义，组建成具有更少编码比特的图拓扑语义模板集合，得到对原图的拓扑语义更好的理解，从而为其他应用和进一步的分析提供基础。

4 结 语

本文考虑对社交网络的拓扑结构，或者说无权无向图的结构进行拓扑语义挖掘。图的拓扑语义事实上包含在其子图的结构中，包括子图的结构语义、子图间的重叠语义以及图的整体语义。通过对图性质的分析，通过逐步合并的方式获得图的子图集合，并通过MDL客观确定了以上各种语义，特别是子图的结构语义和子图间的重叠语义。综上所述，对于网络的拓扑语义挖掘是网络结构信息挖掘的重要方式，也是图数据理解的重要手段之一。