基于捕猎者-猎物模型的干扰与通信抗干扰动态过程*

夏 志，陈建忠 ，牛英滔，韩 晨，逄天洋，马建坤

（1.陆军工程大学 通信工程学院，江苏 南京 210007；2.国防科技大学 第六十三研究所，江苏 南京 210007）

0 引 言

军事无线通信系统是信息化战场的“神经”，是敌方首要攻击和破坏的目标之一。军事无线通信系统能否在恶劣的电磁环境中保持可靠有效通信，已成为各国研究的重点[1-2]。

传统无线通信抗干扰技术主要包括跳频、直扩、自适应陷波等技术。这些技术能够有效应对传统的固定干扰样式，如部分频带阻塞干扰、梳状干扰等。为应对动态、精准、高效的新型干扰[3]，部分文献提出调制、编码、频率、功率都可根据干扰环境自适应改变的多参数自适应通信技术，并提出了基于遗传算法、模拟退火算法、粒子群算法等人工智能算法的通信抗干扰决策引擎[4-6]，实现了对多个通信参数的智能调整。到目前为止，上述文献都局限于静态的干扰环境，对干扰环境下无线通信系统的动态特性及其整体通信性能研究较少。文献[7]中提出，将生物学中的捕猎者-猎物模型用于研究认知无线电系统中主次用户对频谱资源的竞争关系，很好地刻画了主次用户占用频谱资源数量随时间变化的动态性。通信与干扰是一对矛盾，本质上也是频谱资源的争夺。这个过程是动态变化的，因此本文借鉴捕猎者-猎物模型，对干扰、通信双方占用频谱资源数量的动态变化过程进行数学建模，刻画干扰方与通信方在对抗过程中的动态特性，最后对通信方与干扰方争夺频谱资源的动态过程进行仿真验证。

1 基于捕猎者-猎物模型的干扰与通信抗干扰模型

1.1 捕猎者-猎物模型

捕猎者-猎物模型（Lotka-Volterra种间竞争模型）[8]是logistic模型（阻滞增长模型）的延伸，是由Lotka和Volterra于20世纪40年代提出的。该模型描述了不同物种间的竞争关系。

假设N1、N2分别为物种1和物种2的种群数量，则两个物种的种群数量有如下关系：

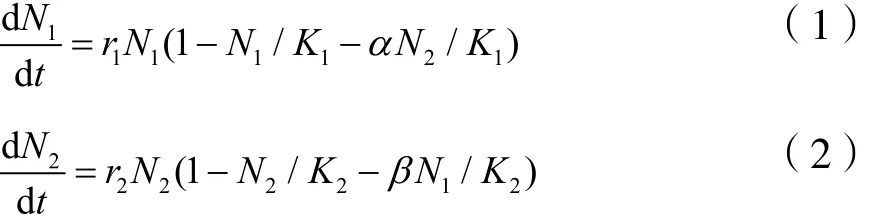
其中K1、K2分别为两个物种的最大环境容纳量；r1、r2分别为两个物种的种群增长率；α为物种2对物种1的竞争系数，即物种2中个体所占用的空间是物种1中个体所占用的空间的α倍；β为物种1对物种2的竞争系数，即物种1中个体所占用的空间相当于β倍的物种2中个体所占用空间。

当物种2可以抑制物种1时，可以认为物种2对物种1的影响大于物种2对自身的影响，即α/K1＞1/K2，即 K2＞K1/α。同理，当物种 2 不能抑制物种1时，K2＜K1/α；物种1可以抑制物种2时，有K1＞K2/β；物种 1 不能抑制物种 2 时，有 K1＜K2/β。当一种物种将另一种物种抑制为0时，成功抑制对方的物种即为得胜。

参数数值不同，可能会产生如表1所示的四种结果。

表1 物种间不同竞争关系下种群的变化情况

1.2 基于捕猎者-猎物模型的干扰与通信抗干扰动态过程建模

将此模型应用到干扰与通信抗干扰的博弈场景中，原理如图1所示。

图1中，将无线频谱资源看作猎物，将干扰方与通信方看作两种捕食者，两种捕食者间存在着对占用频谱资源的竞争关系。干扰方以一定的概率对通信方进行侦察并实施瞄准干扰；通信方则以一定概率接入空闲信道进行通信。当通信方与干扰方发生碰撞时，通信方必须放弃当前的频谱资源，重新占用其他空闲频谱资源；通信方会话结束后将所占用频谱释放，干扰持续时间结束后将所占用频谱释放。通信方不断占用空闲信道进行通信，由于受干扰的影响，其所占用的频谱资源数量会不断变化，在一定时间后会趋向于一个定值，此时称通信方数量达到平衡，而该定值称为通信方的平衡点。干扰方的数量会跟随通信方数量的变化而变化，最终也会趋向于一个定值，此时称干扰方数量达到平衡，该定值称为干扰方的平衡点。

为便于研究，对干扰与受扰的无线通信系统作出以下假设。

（1）通信频谱被划分为N个在频域上互不重叠的信道，每个信道带宽为Wch。信道状态分为三种：当通信方使用某信道进行通信时，该信道为通信信道；当信道被干扰方干扰时，为被干扰信道；当信道未被使用且无干扰时，为空闲信道，空闲信道数为Nf。

图1 通信方与干扰方的捕猎者—猎物模型

（2）干扰信号采用瞄准脉冲干扰，干扰带宽Wj=Wch。每段干扰持续时长Tj。干扰机每隔T会对空闲信道和通信信道进行干扰，不会干扰被干扰信道，且最多可同时释放Nj段干扰（Nj＜N）。干扰机侦察到通信信号并成功实施干扰概率为Ps，对空闲信道产生虚警并成功实施干扰概率为Pfa。

（3）通信方用户总数为Nc，每个用户数通信会话时长为Tc。用户排队进行通信，完成通信的用户排到队尾准备下次通信。

（4）通信方具有一定的认知能力，即每隔T对信道状态进行检测，通信方会选择空闲信道进行通信。若在通信过程中检测到干扰，则中断通信，并于下一秒切换到其他空闲信道继续进行通信。

（5）通信方占用空信道进行通信的接入概率为Pc，对干扰的检测概率为Pd。

（6）定义单位时间内单独占用某一信道的用户为活跃用户，数量用S表示；干扰方、通信方活跃用户数分别定义为Sj、Sc。通信性能可用单位时间系统中通信方活跃用户数来衡量。单位时间系统中，通信方活跃用户数越多，通信方抗干扰能力越强。

2 干扰与通信抗干扰动态过程平衡点及效用函数求解

2.1 平衡点求解

根据上文抗干扰模型的描述，在t时刻通信方活跃用户数满足以下关系：

其中，Gc(t)为与通信方活跃用户增长机制有关的增长函数，Lc(t)为与通信用户传输模型有关的损失函数。

假设在每个时隙中通信用户都能够完成传输工作，即干扰持续时长、通信会话时长均不大于一个时隙，则有：

结合式（3），可推出：

由于Gc(t)与当前的通信活跃用户数量有关，其可表示为Sc(t)的函数，则有：

若通信方活跃用户数量达到平衡，则Sc=Gc(S)至少存在一个解。该问题在数学上属于不动点问题[9]。

Sc(t)∈[0,Scmax]，Scmax是通信网络中的总用户数。[0,Scmax]是一个欧几里得空间的紧凸子集，即实直线R中每个有界闭区间都是紧凸的。同时，增长数Gc[t,Sc(t)]∈ [0,Scmax]，且 Gc[t,Sc(t)]函数在 [0,Scmax]上是连续的，故Sc(t+1)=Gc[t,Sc(t)]在[0,Scmax]上必有解，平衡点存在。

同理，设Sj(t)为总受扰信道数，Gj(t)为新增受扰信道数，Gj(t)与当前的干扰数量有关，可表示为Sj(t)的函数：

则式（7）至少存在一个解，即干扰方活跃用户数的平衡点存在。

2.2 干扰方与受扰通信方占用频谱数量关系与效用函数

定义t时刻试图接入信道的通信用户数与干扰数分别为Mc(t)、Mj(t)。

干扰方通过占用空闲信道获得的频谱资源增长量为：

干扰方通过干扰通信信道获得的频谱资源增长量为：

通信方选择空闲信道接入，一部分将被干扰，被干扰的信道数为。每成功接入一个信道，则试图接入信道的通信用户的数量空间将减少。于是，通信方通过占用空闲信道获得的频谱资源增长量为：

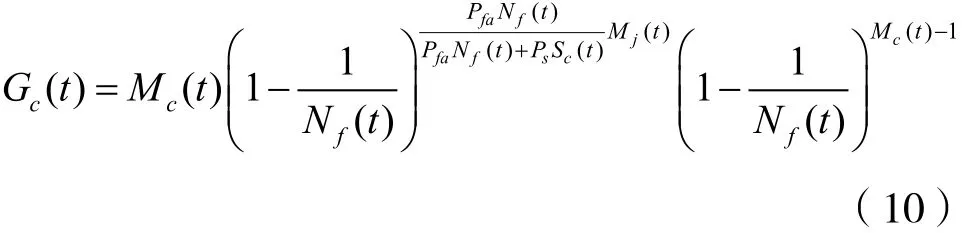
通信信号在t时刻接入某空闲信道，则下一时隙未受干扰继续传输的概率为：

在t时刻后的第3个时刻，通信信号在传输过程中未被干扰的概率为：

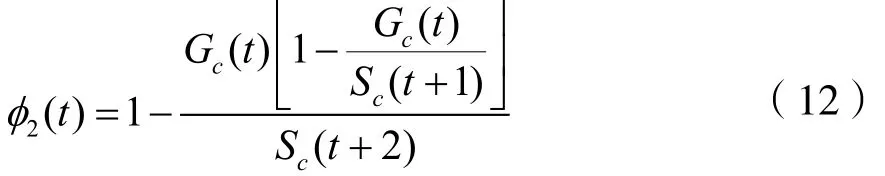
S(t)的数量随时间变化满足：

已知信道数量的变化率满足：

通信用户占用信道的变化率为：

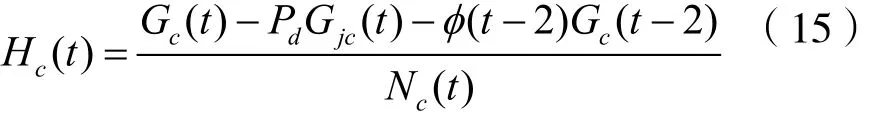
受扰信道数量的变化率为：

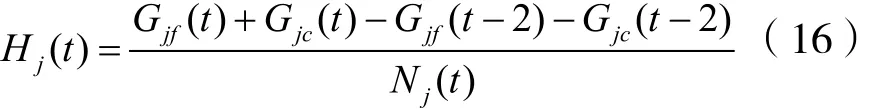
定义达到平衡时的平衡点F(t)为效用函数。

则通信方用户的效用函数为：

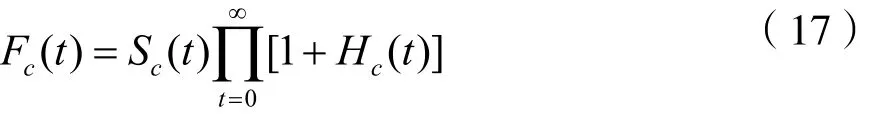
干扰方的效用函数为：

3 仿真及分析

仿真中设置通信信道数N=200；通信用户总数为Nc=150，通信用户成功建立通信概率Pc=0.9，对干扰的检测概率为Pd=1。干扰机侦察到通信信号并实施干扰概率为Ps=0.7，对空闲信道的虚警概率为Pfa=0.05。干扰持续时长与通信时长均设为3 s，即T1=T2=3 s，干扰实施间隔Tj=1 s，通信检测间隔Td=1 s。

图2为干扰机最多可同时释放干扰数Nj=120时，通信方与干扰方每个时刻所占用的信道数量。通过仿真获得的理论值与实际值的比较，通信方与干扰方所占用的频谱资源随着时间的推移都能够逐渐达到各自的平衡值，证明了平衡点的存在；实际值围绕理论值上下波动，基本拟合，说明了该模型适用于通信、干扰双方所占用的频谱资源随时间的变化关系。

图3给出了在干扰机最大可干扰信道数不同时，通信方、干扰方各个时刻各自占用信道数量。可知，干扰机最大可干扰信道数越大，即干扰机干扰能力越强，干扰方平衡点值越大，即干扰方所占用的频谱资源越多；通信方平衡点值越小，即通信方所占用的频谱资源越少，通信方受干扰方影响较大。

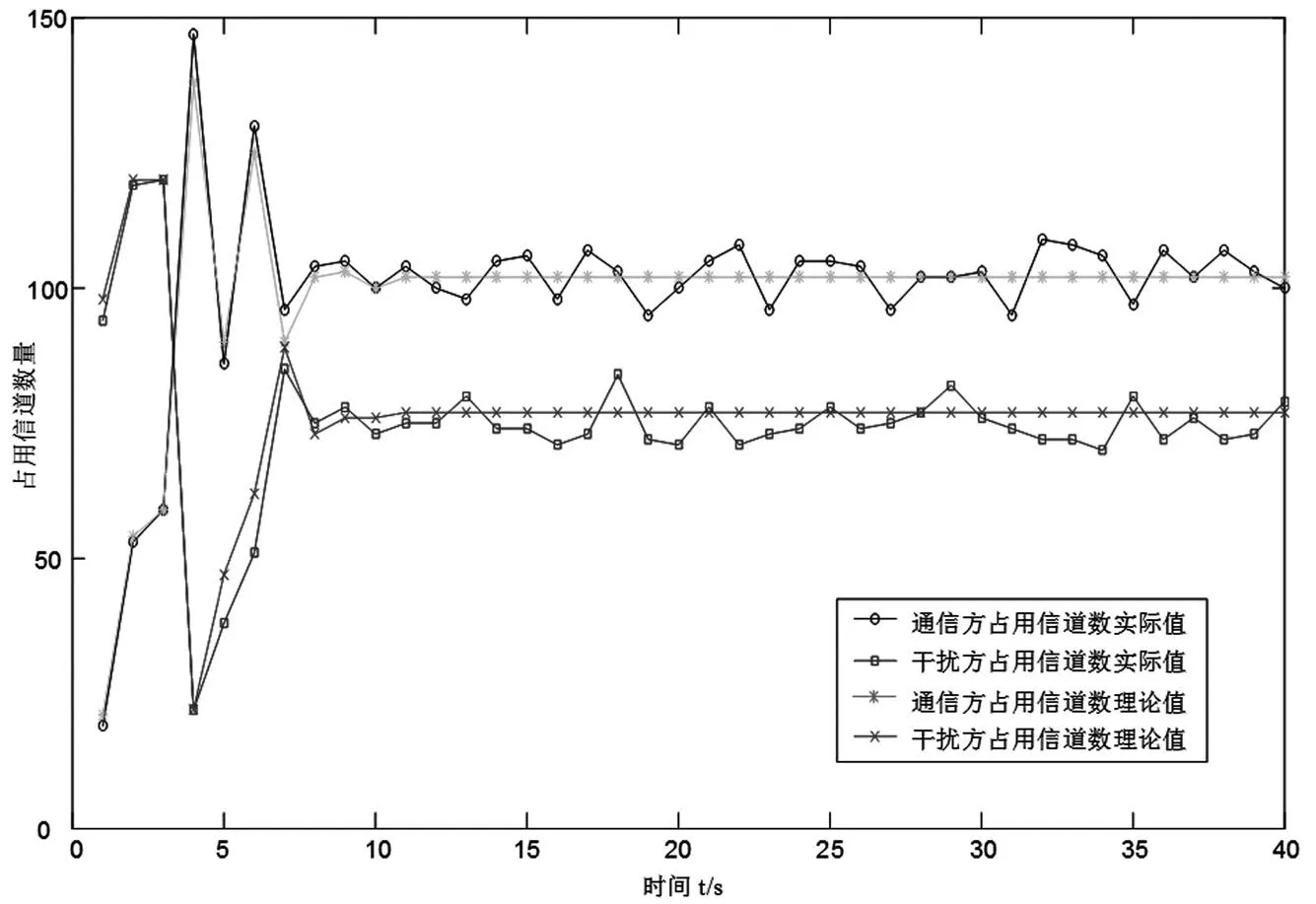
图2 通信方、干扰方占用信道数量随时间的变化关系图（Nj=120）

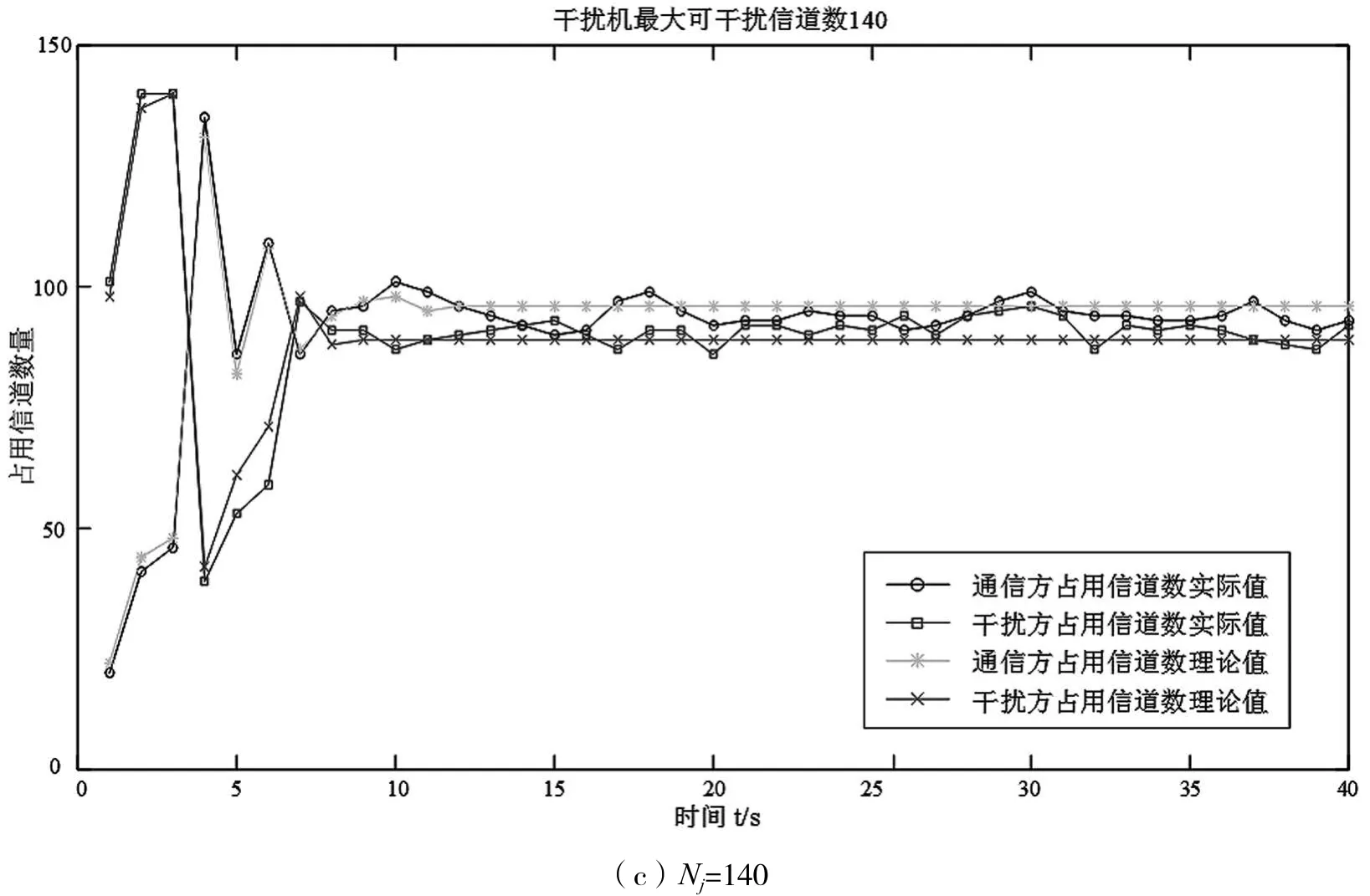
图3 干扰机最大可干扰信道数Nj不同时,通信方、干扰方占用信道数量随时间的变化关系

图4 给出了在干扰机侦察到通信信号并成功实施干扰概率不同时，通信方、干扰方各个时刻各自占用信道数量。可知，干扰机干扰概率越高，即干扰机侦察能力越强，干扰方平衡点值越大，即干扰方所占用的频谱资源则越多；通信方平衡点值越小，即通信方所占用的频谱资源越少，通信方受干扰方影响较大。

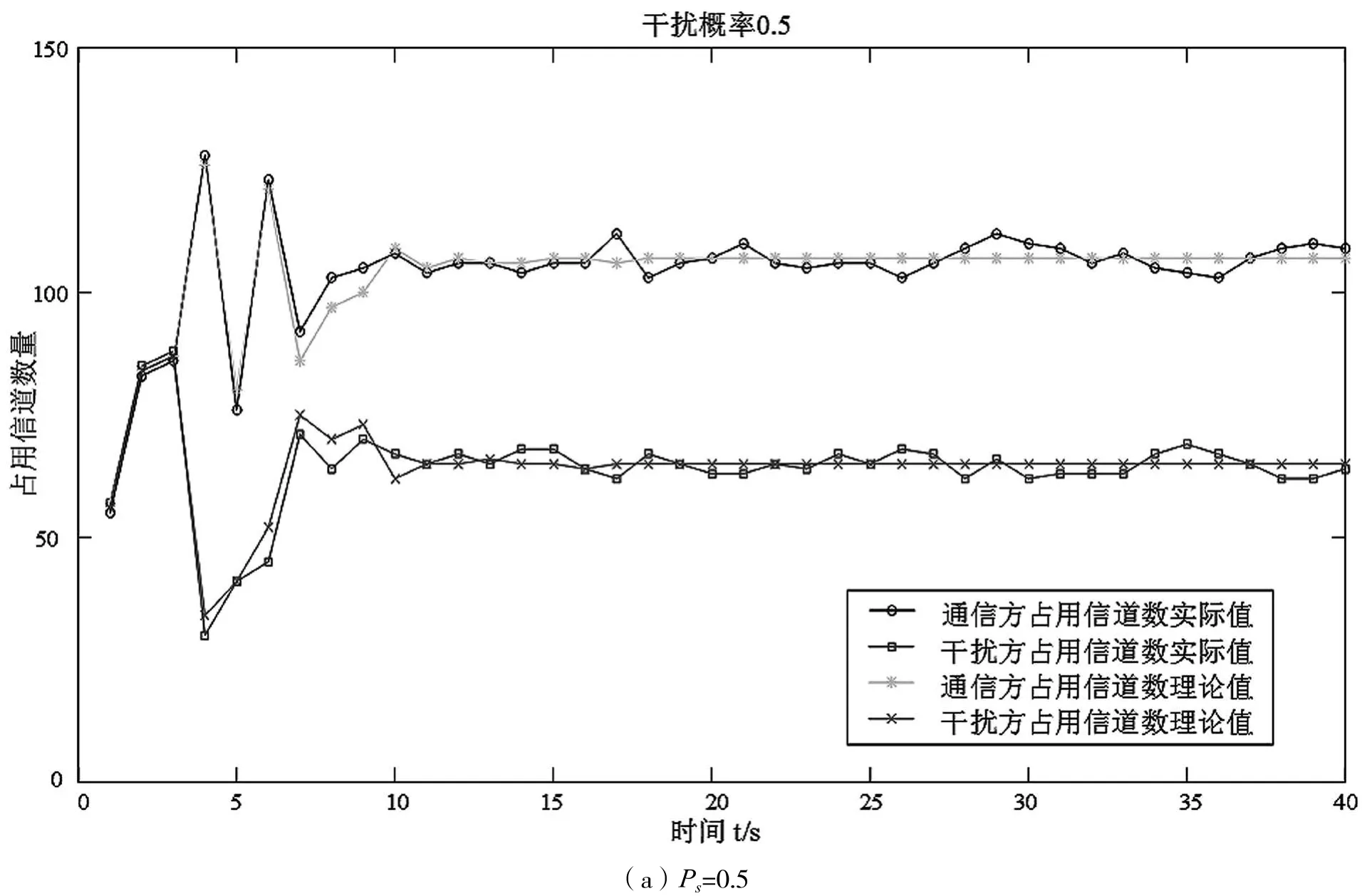
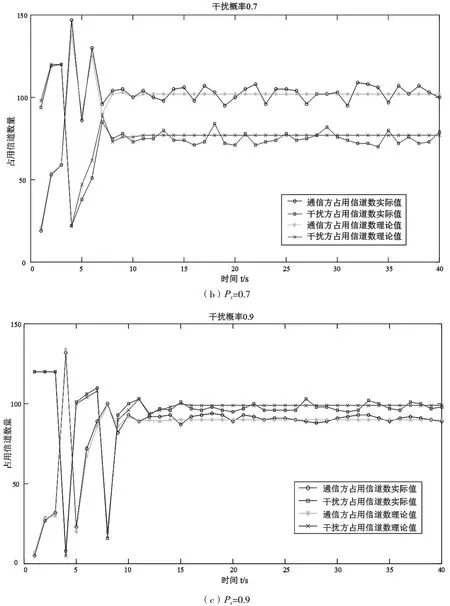
图4 干扰机干扰概率Ps不同时，通信方、干扰方各自占用信道数量随时间的变化关系

4 结 语

本文针对通信方受到敌方干扰时攻防双方对频谱资源争夺的这一动态化博弈过程，提出了一种基于捕猎者-猎物模型的干扰与抗干扰动态过程研究方法。文中干扰方采用瞄准式干扰，在给定的侦察概率下对通信方进行干扰；通信方的多个用户排队进行通信，若检测到受扰，则立即改变信道至空闲信道；完成通信的用户排到队尾准备下次通信。通过分析每个时刻信道中通信用户的数量来衡量系统的通信性能，同时对干扰方与通信方占用信道数量随时间的行为过程进行了理论推导。仿真结果表明，干扰机干扰概率越高或者干扰机最大可干扰信道数越大，即干扰机对通信方的干扰能力越强，干扰方所占用的频谱资源越多，通信方所占用的频谱资源越少，通信系统的性能越差。未来的工作重点主要时采取不同抗干扰技术措施时干扰与通信双方的动态性能变化情况。