大型甚低频伞形天线地损耗电阻的分析与计算*

代甘来，董颖辉，康 颖

（海军工程大学 电子工程学院，湖北 武汉 430033）

0 引 言

甚低频伞形天线的体积庞大，但为电小天线，辐射电阻一般只有零点几欧。因此，设计时要通过铺设地网使天线的地损耗电阻尽可能小[1]，以达到天线辐射效率的要求。在天线参数和地质条件确定时，地网如何铺、铺多大、多密等，是一个需要解决的问题。目前，对甚低频发射天线地损耗电阻的计算主要依靠FEKO、NEC等电磁数值仿真软件。这些软件在计算地损耗电阻时需要对天线结构进行分段[2]，若分段尺寸不同[3-4]（均满足软件要求的段长度λ/1 000＜l＜λ/10，λ为工作波长），计算结果差别较大，而实际天线的电阻是与剖分尺寸无关的。根据文献[5]，天线地损耗为电场损耗电阻和磁场损耗电阻之和，分别由天线近场区的电、磁场分布确定。具有大型顶负载的甚低频天线所产生的电场损耗电阻，相比于磁场损耗电阻可忽略不计。所以，天线近区的地损耗电阻主要由磁场分布确定。文献提及，当顶负载半径不超过下引线高度2倍时，顶线产生的磁场损耗可忽略不计。然而，大型甚低频伞形天线为了增加天线功率容量，顶负载半径一般都要超过3倍的下引线长度。显然，文献的方法不适合实际工程计算。本文供的计算方法可计算任意顶线、不同地质、不同形式的辐射状地网条件下的地损耗，并且计算速度快，计算结果精确且唯一。

1 计算方法

伞形天线的模型及具体参数如图1所示。天线工作频率为f，架设在电导率为σg的大地上；下引线高为h，线径为d2，天线从底端馈电，输入电流为I0，顶端电流为I1；水平顶线由n2根长为b、线径为d3的导线组成；地网由n1根线径为d1、长为a的导线组成。ρ为地面某点距天线根部的距离，地网导线间隔为 s=2πρ/n1。

图1 伞形天线模型

天线磁场损耗是天线周围产生的磁场在地中感应的电流流经大地时发生的损耗[5]。一般来说，甚低频发信天线的地损耗大部分集中在地面切向磁场Hφ和I0的同相区，即ρ≤λ/2π的区域。若用A表示近场区的面积，根据边界条件，天线总的磁场损耗电阻RH可表示为：

其中，Zg为有效复数表面阻抗；Hφ(ρ,0)是天线在地面产生的切向磁场方位向分量复数均方根值；I0是下引线根部的输入电流均方根值；R´H为天线近区内的单位面积磁场损耗电阻，可分为地网区内的单位磁场损耗电阻R´H1和地网区外的单位磁场损耗电阻R´H2。根据式（1），需要计算天线近区任意点的R´H和Hφ(ρ,0)。

1.1 单位磁场损耗电阻的计算方法

据文献[5]，地网区内接地系统的有效表面阻抗Zg由地波阻抗Ze和地网阻抗Zs并联组成，其实部为地网区内的R´H1，可表示为：

在地网区外，仅有地波阻抗Ze，R´H2可表示为：

1.2 下引线的磁场分布

对于辐射状顶负载的直立天线，其天线的等效高度[5]he可表示为：

其中，Co为输入端到天线水平部分末端的对地总电容，由垂直部分电容[5]CV和水平部分电容[5]CH相加所得。

CV和CH分别可表示为：

在甚低频频段，天线下引线上的电流可看成是线性分布的。若归算到输入电流I0，天线等效高度又可近似为：

所以，由式（5）即可求出下引线顶端电流I1。

若将下引线归算为电流均匀分布的直立天线，根据边界条件和相关几何关系[6-7]，计算其在地面磁场的表达式H1φ为：

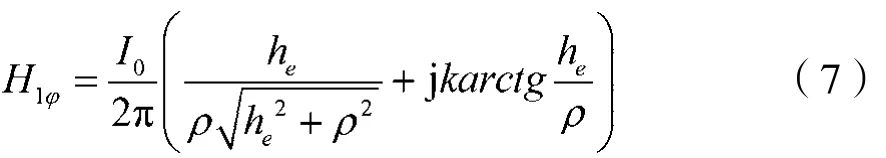
将H1φ分解成X轴、Y轴两个方向的分量，下引线的磁场H1φ可表示为：

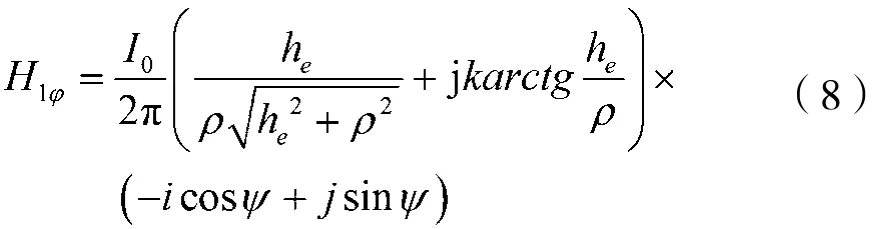
其中，k为自由空间相移常数，i、j分别表示X轴和Y轴的正方向，Ψ为地面某点与天线根部的连线和Y轴正方向的夹角。

1.3 顶线的磁场分布

对于单根水平顶线建立如图2所示的坐标系。此时，顶线在地面任意点产生的磁场始终垂直于Y轴。由于b≪λ，天线顶线上的电流分布可近似看成线性分布，可表示为：

其中，I2=I1/n2为单根顶线输入电流。

图2 单根顶线在地面的磁场

根据边界条件及相关几何关系[6-7]，计算单根水平顶线在地面任意点产生的电磁场表达式为：

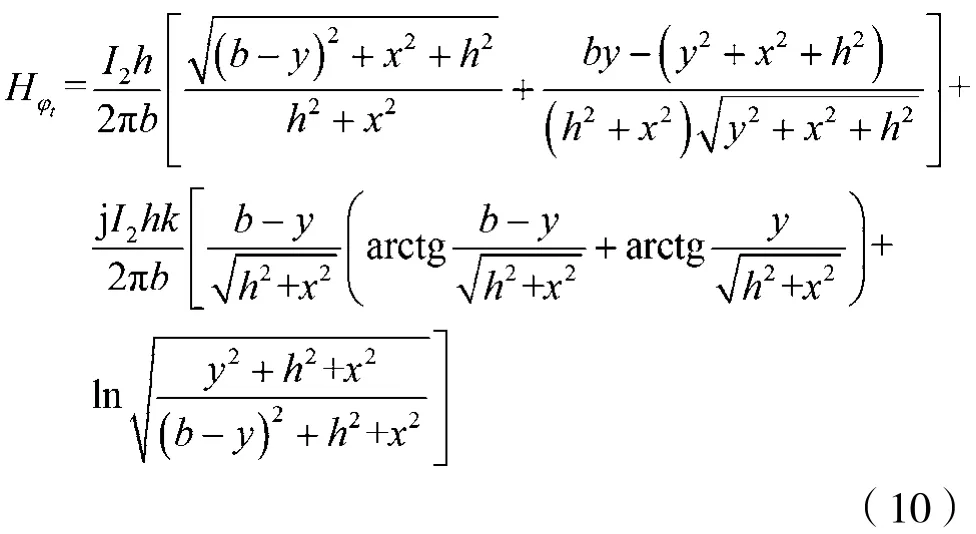
当加载n2根均匀分布的辐射状水平顶线时，可建立如图3所示的坐标系进行分析。规定第1根与Y轴平行，其他顶线编号t按逆时针顺序编号。

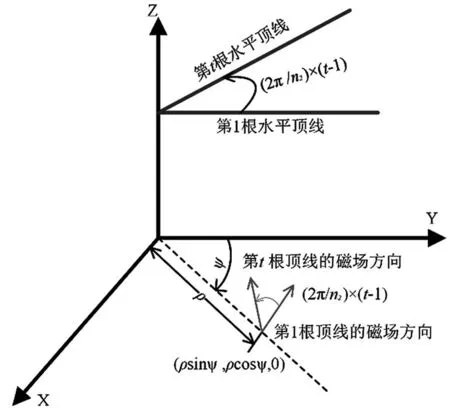
图3 坐标系转换

用极坐标代替直角坐标系，所以任一根水平顶线在地面的磁场可表示为：

其中，ϑ=φ+2π(t-1)/n2。

所以，n2根均匀分布的辐射状水平顶线在地面的磁场强度为：

将下引线和顶线产生的磁场矢量相加即为整个天线的合成磁场。

2 计算案例及分析

为验证本文计算方法的正确性，表1给出了f=20 kHz、h/λ=0.025、地网根数 n1=50、接地参量分别为0.03和0.1时，小顶负载的甚低频发射天线在不同地网长度a下的磁场损耗（损耗单位均为Ω）。

表1 磁场损耗对比

从表1可以看出，本文计算结果与文献[5]吻合较好，可证明本文所述方法在计算小顶负载的甚低频发射天线磁场损耗是正确的。

图4给出了工作在20 kHz的下引线高300 m、顶负载为48根1 000 m的甚低频伞形天线在根部输入电流为1 A时，本文计算方法与FEKO仿真软件（分段为λ/800）计算的近区的磁场对比图。

图4 近区磁场对比

图4 可知，文中计算方法与仿真软件计算结果基本吻合，证明了该方法在计算大顶负载天线磁场分布的正确性。

图5给出了工作频率f=20 kHz、下引线h=300 m、顶负载根数n2=48根、不同顶线长度b时，顶线与下引线产生的磁场在地面的比值随ρ的变化曲线。图6给出了上述天线形式下，Tg=0.03，地网根数n1=100根时，磁场损耗电阻随不同地网系统半径的变化曲线。

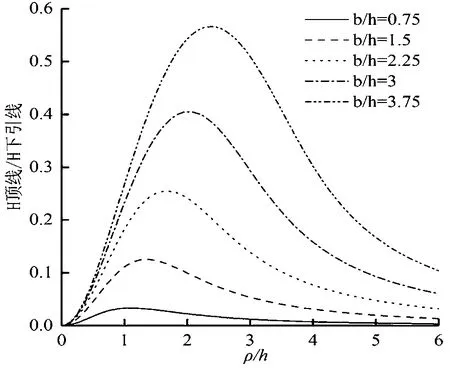
图5 不同顶线长度下，顶线磁场与下引线磁场比值

从图5、图6可知，对小顶负载（b/h≤1.5）的甚低频天线，其顶线磁场相对于下引线最高不超过13%，带来的磁场损耗也可以忽略不计。当顶线长超过下引线2倍后，以图6中b/h=3.75的曲线为例，当地网半径a≥0.08λ后，顶线带来的损耗几乎与下引线相当，即证明大顶负载带来的损耗不能忽略。此外，从图6可看出，地网根数不变且地网系统半径达一定规模后，继续增加地网系统半径对减少损耗并无明显效果。可见，当地网根数确定后，单纯增加地网铺设半径对提高天线辐射效率的效果是有限的。

图6 不同顶线长度下，磁场损耗电阻随不同地网系统半径的变化曲线

图7 给出了工作频率f=20 kHz，下引线h=300 m，顶负载根数n2=48根，顶线长度900 m，假设接地参数Tg=0.03时，在3种不同地网总长情况下，地网系统半径与磁场损耗电阻的关系。图7中地网总长160 km、a/λ=0.107的地网铺设情况即为图6中顶线长度是下引线3倍、a/λ=0.107时的情况。

图7 不同地网总长下，磁场损耗电阻随不同地网系统半径的变化曲线

从图7可知，当地网半径相同时，地网总量越大，即地网铺设越密，磁场损耗电阻越小。可见，铺设较密的地网对减少损耗效果明显。当地网总量较小时，地网半径越大，其损耗电阻反而越大；当地网总量达到一定规模后，地网半径越大，磁场损耗电阻越小；若地网总量介于两者之间，随着地网半径的增加，损耗电阻先减少后增加，存在一个地网最佳铺设半径。

3 结 语

研究计算甚低频伞形天线的磁场损耗电阻的解析法，计算案例中磁场损耗电阻和磁场分布的计算结果分别与文献数据和FEKO仿真结果吻合良好，计算速度远高于基于矩量法的仿真软件FEKO。为了得到较高的计算精度，在计算磁场损耗电阻时，不能忽略天线磁场含虚部的部分。对于顶负载较小的甚低频发射天线，由顶负载带来的损耗电阻可忽略不计。当顶线半径大于下引线长度2倍时，由顶线带来的磁场损耗便不能忽略。在设计伞形天线地网时，加大地网铺设密度，对降低磁场损耗电阻十分必要。在天线形式和架设地面电导率确定的情况下，地网总量对天线效率的影响很大。若地网总量不够，地网铺设半径越大，磁场损耗电阻会越大，不利于提高天线效率；若地网总量达到一定规模，地网铺设半径越大，磁场损耗电阻会越小；若地网总量在上述两个临界条件间，则存在一个最佳地网铺设长度。因此，在设计天线地网时，为获得较高的效费比，可根据天线形式、地质条件以及要达到的辐射效率，确定辐射状地网的最佳铺设形式。