外插脉冲响应FIR滤波器系数敏感度参数研究*

李伟琪 ，王 浩 ，赵晨子 ，王 翀

（1.杭州电子科技大学 通信工程学院，浙江 杭州 310018；2.江苏省电力公司 信息与通信分公司，江苏 南京 210000）

0 引 言

与IIR滤波器相比，FIR滤波器具有绝对稳定性和线性相位的优势。然而，当对滤波器的频域性能要求较高时，FIR滤波器则需要很高的阶数，使得FIR滤波器硬件执行的复杂度（硬件执行复杂度通常由硬件设计时所需的乘法器和加法器数目衡量）和系统的群延时很高。因此，在不影响FIR滤波器频域性能的前提下，减少其硬件执行复杂度，具有重要的研究意义。

为降低FIR滤波器的硬件执行复杂度，许多研究者对其进行了研究。经文献调研，关于低复杂度FIR滤波器的研究最早始于1980年文献[1]提出的系数过采样方法；1983年，文献[2]提出了基于递归取和滤波器的预滤波器-均衡器结构，文献[3]提出了一种分段指数近似的方法，但由于量化误差的影响，合成的滤波器可能是无限冲激响应；1984年，文献[4]提出了一种内插脉冲响应方法；1985年，文献[5]提出了一种基于预测编码的方法，用于减少FIR滤波器系数的字长；1986年，文献[6]提出了一种非常有效的低复杂度FIR滤波器设计方法——频率响应罩FRM（Frequency Response Masking），通过构造原型FIR滤波器的互补FIR滤波器以克服内插法通带宽度较窄的缺陷。内插法可看作是FRM方法的特例。FRM方法虽然频域性能（即硬件执行复杂度）优越，但在滤波器长度方面仍有缺陷：在相同频域性能指标的前提下，所合成的FIR滤波器通常比传统方法（直接最优化方法或者经典的Parks-McClellan方法）设计的滤波器具有较高的阶数。1990年，文献[7]基于低通或者高通FIR滤波器系数的类周期性，提出了外插脉冲响应EIR（Extrapolated Impulse Response）方法，可大幅降低滤波器的执行复杂度，且其合成的滤波器总是有限冲激响应，后有若干文献对外插法进行了研究。1996年，文献[8]通过混合整数线性规划的方法设计了具有稀疏系数的FIR滤波器。2010年，文献[9]基于压缩感知理论研究了具有稀疏系数的FIR滤波器设计。

虽然原始EIR滤波器设计由Lim Y C先生等人[7]于1990年提出，但发展缓慢。由于原始EIR滤波器设计中仅有尺度向量通过线性规划的方法优化获得，2004年Yu Y J等人[10]提出了采用半无限规划的方法联合优化原始EIR滤波器设计中的所有未知系数，改进了原始EIR滤波器的频域性能。2005年，Yu Y J等[11]将外插法与频率响应罩法结合用于降低FIR滤波器的硬件执行复杂度。2008年，Zhou L H等人[12]提出了基于主成份分析的外插法，通过两步骤外插改善了EIR滤波器的频域性能。此外，Cao Y F等人[13]于2011年研究了离散系数的EIR滤波器设计。王浩等人于2012年[14]、2013年[15]和2015[16]年对外插法的结构和系数优化算法进行了进一步深入研究。

文献[17]首次提出了EIR滤波器的系数敏感度CS（Coefficient Sensitivity）参数概念，并通过约束该参数以实现低量化效应EIR滤波器的设计。然而，文献[17]并未给出CS参数的严格数学推导和仿真实验分析。本文将对该参数进行严格的数学推导，并给出具体的实验仿真分析。

1 系数敏感度参数推导

EIR滤波器的系数参数包括三部分：不变系数x、基本向量参数r1,r2,…,rp和尺度向量参数s1,s2,…,sp。为叙述方便，这里仅考虑两个基本向量p=2的情况，三个或者更多基本向量的情况可以类推。令Δx、Δrn、Δsn为系数x、rn、sn(n=1,2)的无限精度浮点表示到有限位数表示的量化误差。那么，量化后的无限精度浮点表示EIR滤波器的频率响应函数可写成如下形式：

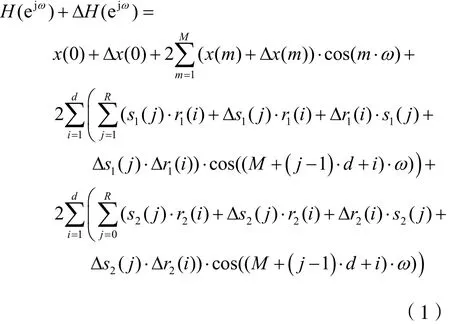
其中H(ejω)为量化前EIR滤波器的频率响应函数，ΔH(ejω)为量化引起的频率响应误差函数。假设|Δx(m)|、|Δrn(i)|、|Δsn( j)|(n=1,2)足够小，舍去式（1）中的二阶误差项，得到：

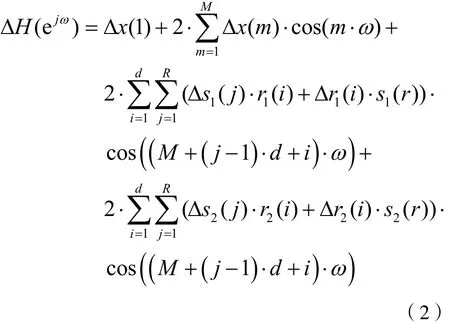
对式（2）的等式两边求平方，得到：

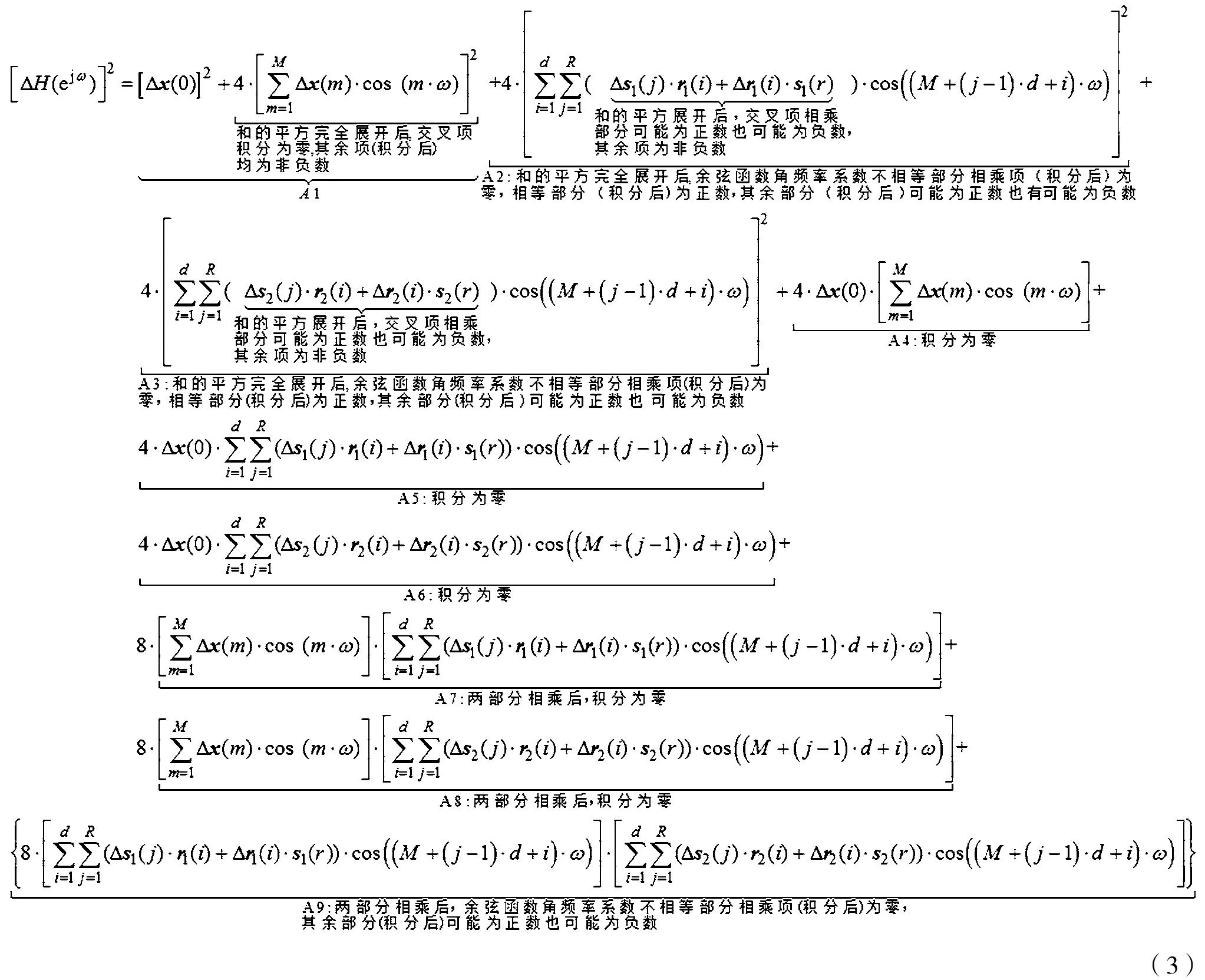
对式（3）在[0,2π]区间进行定积分。根据三角函数公式，两不同角频率系数的余弦函数乘积可转化为两余弦函数之和，而式（3）中余弦函数的角频率系数均为正整数，所以两不同角频率系数的余弦函数积化和差后的两余弦函数的角频率系数依然为正整数。对于这些余弦函数，在[0,2π]区间内的定积分值为零，那么可得量化误差函数为：

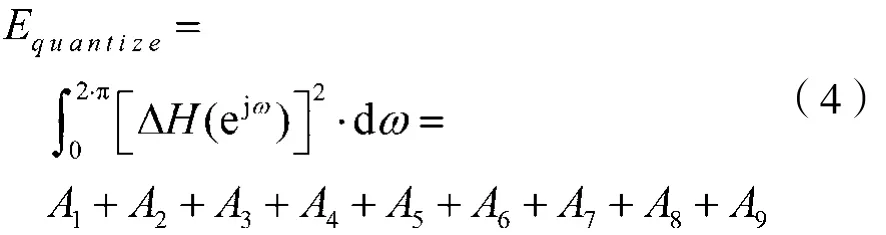
其中：

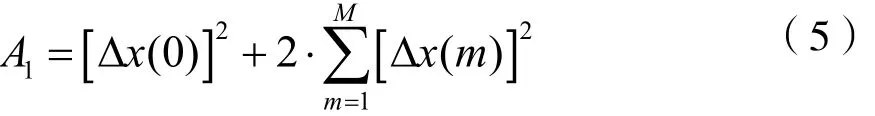
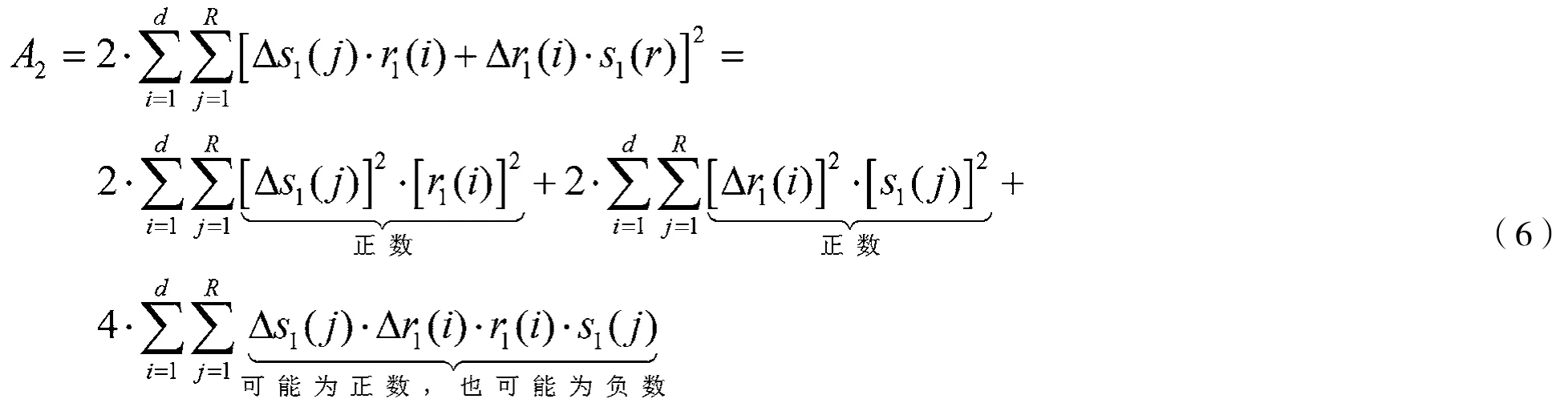
由于影响量化误差函数Equantize的变量很多，为方便分析该函数，令：

并用 ε2替换 A1,A2,…,A9中的 [Δx(m)]2、[Δrn(i)]2、[Δsn( j)]2(n=2)。该部分近似较实际值偏大，属于保守估计。根据量化误差变量的随机性和不相关性，假设A2、A3和A9中可能为正数也可能为负数的部分的累加和等于零（如果将这些部分当成随机变量，那么这些随机变量在理论上的数学期望值也为0）。通过以上简化分析，可得：

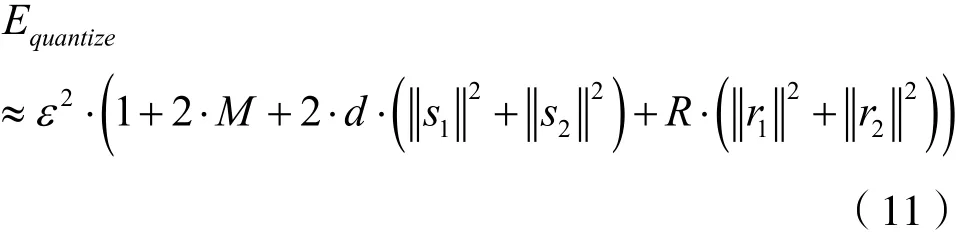
在给定参数M、d和R的情况下，可定义系数敏感度参数[17]如下：

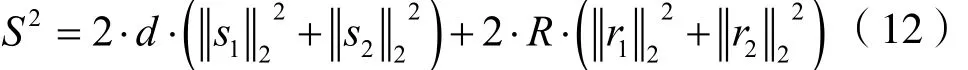
回顾推导过程，系数敏感度参数的导出可以推广至基本向量数目p为任意值的情况，即：

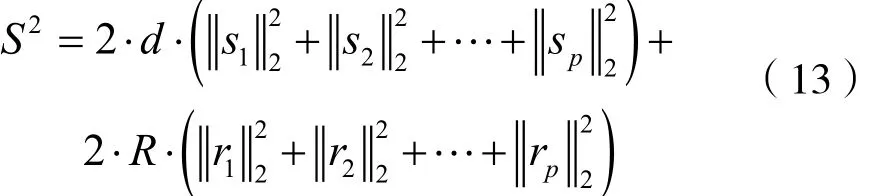
讨论1：CS参数首先由文献[17]提出，文章推导结论与其一致。然而，文献[17]中的EIR滤波器的基本向量数目不大于2，这里指出CS参数也可推广至任意基本向量数目的情况。此外，文献[17]在推导过程中，基本思想是分析量化误差函数Equantize的数学期望，与文章基本思想不同。最后，上述推导仅考虑偶对称FIR滤波器，回顾推导过程，式（13）结论依然适用于奇对称FIR滤波器。

讨论2：CS参数的意义在于，如果有两个EIR滤波器频率响应性能相同但滤波器系数不同，且其中一个EIR滤波器的CS参数明显小于另外一个EIR滤波器，那么应当选择具有明显较低CS参数的EIR滤波器，以减少滤波器硬件执行时的量化误差。

讨论3：回顾推导过程，Equantize描述EIR滤波器量化前后的频率响应积分最小二乘误差。Equantize函数值为零，意味着EIR滤波器无量化误差。但是，较低的Equantize函数值并不一定意味着较好的频率响应指标。此外，CS参数是Equantize函数的近似表达，较低的CS也不一定意味着较低的Equantize函数值。

讨论4：滤波器优化设计准则通常包括最大误差最小化准则和最小二乘准则。显然，较小的Equantize并不一定意味着较小的上述准则下的误差。

2 实验仿真分析

下面通过仿真实验观察CS参数值大小与系数量化之间的关系。首先通过Parks-McClellan最优化滤波器设计方法设计一个201阶低通滤波器。该低通滤波器的通带和阻带归一化截至频率为0.6和0.62。然后，设计EIR滤波器参数如下：M=10，d=10，R=9，p=2，p个基本向量的L2范数相等。由于基本向量的L2范数直接影响所设计EIR滤波器的CS参数（参看式（12）），仿真实验通过改变p个基本向量的L2范数来获得具有不同CS参数的EIR滤波器。最后，采用CSD（Canonic Signed Digit Code）编码技术对上述EIR滤波器系数进行量化，每一个EIR滤波器量化时的数据比特数设置为15（2～12，14，16，18，20）种情况。注意到，若以连续系数计算这些EIR滤波器的频域性能，这些滤波器的频域性能全部都相等。

图1描述的是不同CS参数和不同量化比特数下的EIR滤波器的峰值纹波幅度PRM（Peak Ripple Magnitude，通带波纹和阻带波纹中的最大值，单位为dB）指标。

从图1可以看出，图1（a）具有明显较高的CS参数值，一般对应着较高的量化误差；图1（b）当量化比特数等于5～12、14、16、18或20时，较高的CS参数值一般情况下对应着较高的系数量化误差（通过量化后EIR滤波器的PRM指标度量），这种对应关系在量化比特数等于5～12、14、16时表现较为突出；图1（c）当量化比特数很低时（等于2，3，4），较高的CS参数值与滤波器量化误差之间并无明显的对应关系，这或许与CS参数值推导中的若干近似（以及该参数本身的其他局限性）有一定关系；图1（d）当量化比特数相对很高时（等于18，20），由于EIR滤波器每一系数的量化误差已经很小，基本观察不到较高的CS参数值一般对应着较高的系数量化误差。

通过以上分析可知，CS参数对于EIR滤波器设计而言并非是完美，然而优化CS参数可在一定程度上降低EIR滤波器的系数量化效应。

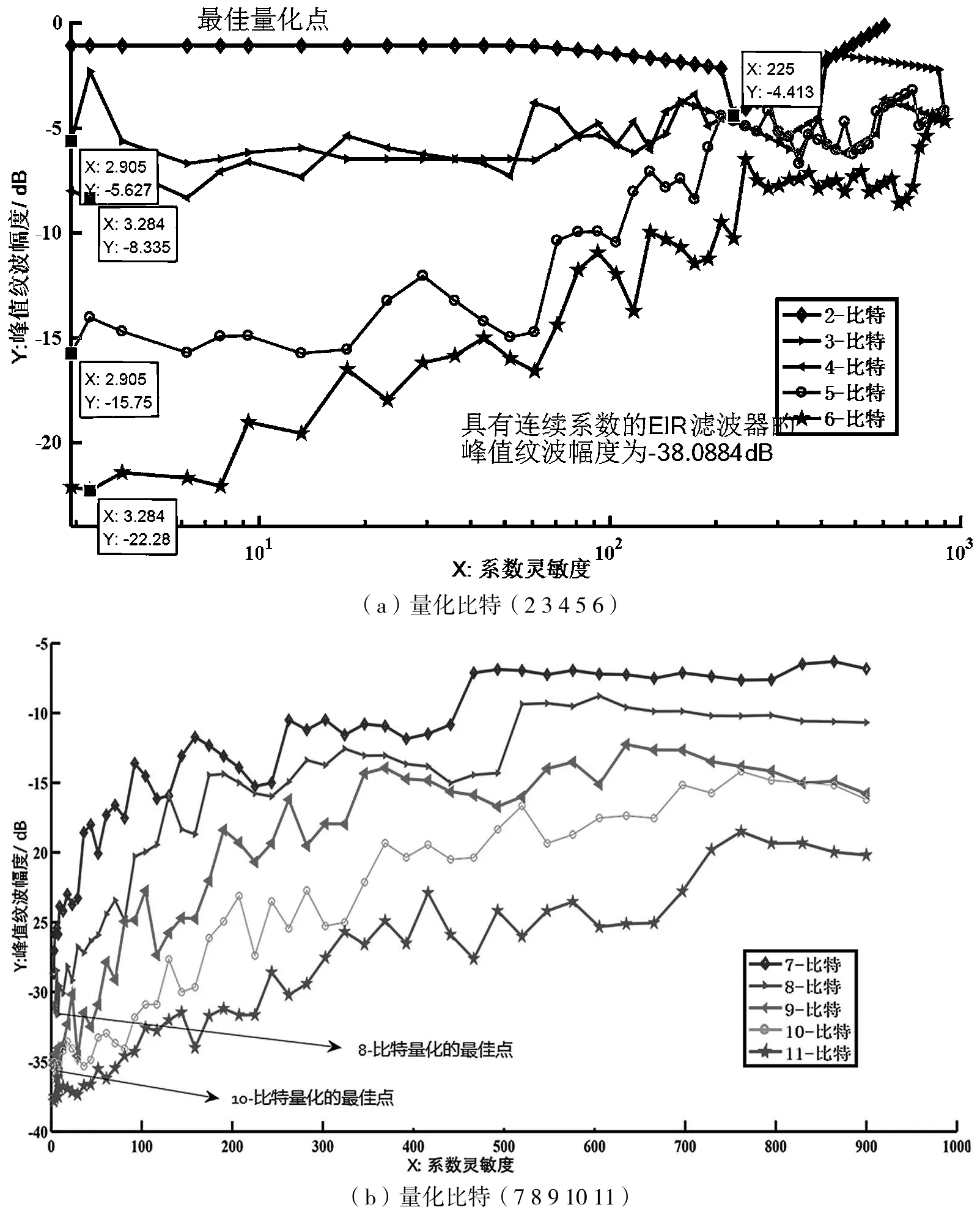
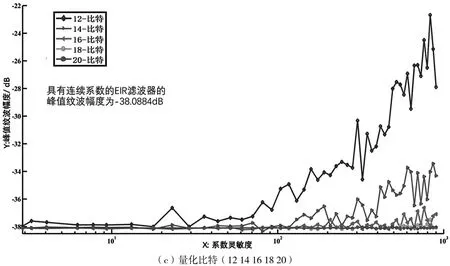
图1 EIR滤波器在不同CS参数值和不同量化比特数下的系数量化

3 结 语

EIR滤波器是诸多低复杂度FIR滤波器中的一种。如何在设计连续系数EIR滤波器时降低其实际硬件执行时的量化效应具有重要的实际意义。系数敏感度参数约束可用于降低EIR滤波器的量化效应，然而关于该参数的严格理论推导以及实验分析未有报道。论文对系数敏感度参数进行了严格理论推导并进行了实验分析。实验结果表明，系数敏感度参数可以在一定程度上有效降低EIR滤波器的量化效应。