超高速碰撞产生的碎片云研究进展
邸德宁, 陈小伟,2, 文肯,, 张春波
(1.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081;2.北京理工大学 前沿交叉科学研究院, 北京 100081; 3.中国工程物理研究院 总体工程研究所, 四川 绵阳 621900)
0 引言
随着人类航天活动的增多,空间碎片环境近年来急剧恶化,各国对航天器特别是载人航天器和空间实验室碎片防护结构设计愈加重视,这一工程背景极大推动了薄板受超高速撞击而产生碎片云的研究工作。国际上已有诸多科研院所和高校对此问题进行了研究,并有两年一届的超高速撞击国际会议,国内更是设立了国家国防科技工业局空间碎片专项项目以促进对该问题的研究。
空间环境中存在着微流星体和空间碎片,共同构成了影响人类航天活动安全的流星体/空间碎片(M/OD)环境[1]。微流星体相对于地球轨道飞行器的平均相对速度为19 km/s[2],主要由微小的陨石和冰等组成。空间碎片主要由铝合金及铝、锌、钛等金属氧化物组成,平均密度为2.8 g/cm3,其绕地球飞行的速度取决于所在轨道[3]。Whipple于1947年提出“双层板防护结构”[4],其基本思想是在航天器舱壁前一定距离处设置缓冲屏,弹丸超高速撞击缓冲屏形成碎片云,使空间碎片的动能被高度分散并部分耗散,实现对航天器的有效保护。近年来有多种新型防护结构被提出,包括新防护结构形式和高性能防护材料,但都是对Whipple防护结构的升级,基本思想未改变。换个角度看,防护结构最外层的缓冲屏和空间碎片撞击后,实际是撞击产生的碎片云侵彻舱壁,因此航天器防护的研究离不开超高速撞击碎片云的研究。
从航天器防护角度考虑,在确定环境下碎片云的分布特性决定碎片云的侵彻性能,进而决定防护效果及航天器安全。碎片云中碎片的形状、大小、速度分布都不均匀,还可能发生碎片材料相变,这些因素深刻影响了碎片云的侵彻性能。从物理过程考虑,弹丸和薄板撞击的各类相关参数,包括弹和薄板的材料、尺寸,弹的形状、撞击角度、撞击速度以及环境因素等,它们决定了碎片云分布特性。在工程方面,需要提出碎片云模型或撞击极限方程,以描述碎片云侵彻性能、指导工程设计。
事实上,国内外对碎片云的研究可分为4类:碎片云形成过程研究、碎片云分布特性研究、碎片云模型研究和碎片云侵彻性能研究。截止目前,已有一些相关综述发表,如:郑建东等[5]关于碎片云模型的综述、柳森等[6]关于中国空气动力研究与发展中心空间碎片实验研究进展总结、曹燕等[7]关于微小飞片激光驱动及损伤效应的总结、韩增尧等[8]关于空间碎片防护研究的最新进展总结,而最近一篇关于碎片云总体研究进展的综述发表于1990年[9]。本文将更新和较全面评述近30年碎片云研究的总体进展,以供相关领域研究者参考并继续研究具体方向进展。
本文针对薄板受超高速撞击过程中正撞击情况下产生的碎片云进行分析,按碎片云形成过程、碎片云分布特性、碎片云模型和碎片云侵彻性能4个部分论述,梳理自20世纪90年代以来的研究进展。除特殊注明外,本文默认撞击条件已足够产生完整的形态碎片云,而不是弹丸穿过靶板后保持完整或初步破裂。
1 碎片云形成过程研究
碎片云形成过程问题在20世纪50年代碎片云研究初期即被关注,但研究进展较慢。研究者们大多针对圆柱形弹体和球形弹丸,前者应力波作用过程分析相对简单,后者便于比较而被广泛接受,主要分析弹丸内冲击波和稀疏波作用过程。此外,薄板上的弹孔情况,特别是弹孔的大小也被广泛分析,以说明薄板破坏机理及对碎片云组成的贡献。
1.1 圆柱形弹体碎片云形成过程研究
圆柱形弹体端面平直且环向对称,与薄板撞击产生的冲击波常被视为平面波;侧面垂直于端面,侧向稀疏波的分析也较为简便,广泛用于冲击波和稀疏波在弹体内相互作用过程的分析。Maiden等[10]基于一维应力波理论提出材料在稀疏波下的破碎可被视为层裂过程,但上述分析仅能说明材料单方向上的断裂问题,难以解释材料在极短时间内碎化为细小颗粒的事实[11]。考虑碎片云速度分布,根据冲击波强度可知初始稀疏波强度,继而可参考层裂理论计算不同层裂碎片速度。然而,目前缺乏此方面的细致工作,机理分析只被用于认知过程,未能推算后续物理现象及碎片云分布特性。
来自薄板背面的轴向稀疏波和弹体侧面的侧向稀疏波快于冲击波,可能追赶卸载弹丸内冲击波。在确定材料及固定薄板厚度下,轴向很短的圆盘形弹体稀疏波来不及追赶冲击波,将导致整个弹体处于拉伸状态而产生碎片云,适合于典型碎片云研究;轴向更长的弹体多用于临界破碎和侵彻分析[12]。汪庆桃等[13]采用数值模拟方法分析了圆柱形长杆弹体撞击薄板时弹体侵蚀长度与弹和薄板材料、几何尺寸及撞击参数的关系,事实上也可借助理论分析得到冲击波被卸载的位置,即弹体完全破碎的临界尺寸[14]。针对不同应用场景,需要按照上述分析考虑弹体和薄板的几何比例极限要求,如航天器防护中需要计算板厚下限。
不同形状弹体所产生的碎片云外形差异较大,但分析认为其形成机理和大体形状是相似的,碎片云外形的差异只是由于弹体外形影响冲击波到达材料自由面的时间,例如柱形弹体轴线附近的冲击波面接近平面,而球形弹丸冲击波面的更接近半球面[15]。进一步可推测:平面冲击波在弹体尾端反射为平面稀疏波,将导致碎片云尾端近似平面结构,而半球面冲击波将导致半球形结构。
张庆明等[16]认为弹体材料不可能完全均匀,因此撞击所产生的冲击波不会是绝对的平面波,将导致材料内出现局部剪切运动而断裂;同时,弹体侧表面和薄板相对运动也将产生剪切力,导致材料出现滑移等。综合来看,弹撞击薄板后应当是剪切和拉伸相互作用而形成碎片云[16]。材料在强冲击下的破坏机理是一大难题,利用数值模拟方法中的失效准则不难验证上述结论,但目前的讨论大多仍基于稀疏波拉伸破坏分析。
形成机理分析不局限于圆柱形弹体情况,但只有个别圆柱形弹体的碎片云模型中定量分析了碎片云形成过程。此外,这些分析尚停留在一维理论,侧向稀疏波强度及衰减缺乏可靠结论,另一方面,形成过程讨论依赖于具体材料失效机理,工程设计中结构改进和材料改进分别对应这两方面。
1.2 球形弹丸碎片云形成研究
球形弹丸形状规范,只需要一个尺寸数据描述,便于比较。球形结构完全对称,不存在撞击姿态问题,被研究者们广泛应用。不同形状弹体的碎片云形成机理相似,但球形结构将导致冲击波在弹丸表面的反射和波系的空间传播及衰减高度非线性,难以利用1.1节的基本理论分析。在实验方面,有研究者使用透明材料厚靶观察弹丸的破坏和冲击波传播过程[17],但效果有限,碎片云形成过程的研究大多基于数值模拟。
Alme等[18]使用任意拉格朗日- 欧拉(ALE)算法计算了直径9.5 mm铝球弹丸以8 km/s速度撞击1.9 mm厚薄板的情况,发现波阵面接近椭球面,压力分布复杂,但明显呈非线性分布。Kipp等[19]利用美国圣地亚国家实验室三维欧拉冲击波软件CTH计算过弹丸内轴线上5个点处的最小主应力(拉应力为负)历程。综合来看,通常所假设的轴线上压力峰值随距离线性降低是不准确的[20]。可以确定,来自球形边界的稀疏波强烈衰减冲击波,但难以完全卸载冲击波,这一衰减过程呈非线性。不同直径球体内稀疏波的产生及相互作用过程高度相似,分析结论普适性强。
考虑碎片云形成过程,以Alme等[18]算例为例,冲击波在0.2 μs左右到达薄板背面并转变为稀疏波,导致薄板发生变形;0.4 μs前弹丸和薄板接触边缘的薄板材料在稀疏波作用下剥离,形成反向溅射碎片云[20]。应力波的作用改变了材料运动状态,考虑弹丸破裂过程及撞击导致的材料速度改变,可推测认为:薄板背面稀疏波强度较高,直接导致薄板从背面开始破裂并加速;弹丸尾端处反射的稀疏波导致尾端开始破裂,材料速度降低;反向溅射碎片说明弹和薄板的接触位置材料亦产生破裂。然而,对于在弹丸中后部传播的冲击波在球体边界反射产生的侧向稀疏波,难以确认其是否足以引起中后部边缘材料破裂。球形弹丸轴向和侧向稀疏波方向不正交,受到源自不同位置的稀疏波作用而破裂的碎片速度改变方向不同。目前可通过数值模拟方法观测稀疏波的分布情况,但缺乏对弹丸材料破裂的具体分析,上述材料破碎过程的推测缺乏验证,难以建立冲击波、稀疏波分布到碎片最终速度的关系。
随着稀疏波对材料的破碎作用结束,一定时间后各碎片以恒定速度独立运动。在大规模数值模拟中,待粒子进入恒定速度后可直接映射粒子的位置,跳过碎片云从薄板后到后续靶板前的扩散过程,大幅压缩计算耗时。同时,这也说明真正决定碎片云分布的只有稀疏波作用的阶段,形成过程研究要尝试建立稀疏波分布模型。
不同于圆柱形弹体情况,球形弹丸与薄板撞击后先是点接触,而后接触面不断扩大。针对球形弹丸与靶板从撞击到开始产生反向溅射碎片的过程,Ang[21]从理论上分析了弹丸和靶板接触点的移动速度,通过其与材料冲击波速的对比决定了反向溅射碎片开始产生的位置。图1为撞击点处速度示意图,通过分析几何及运动学关系得到:
(1)
式中:vtc为靶板上撞击点移动速度;vpc为弹丸表面撞击点移动速度;τ为撞击开始后时长;D为弹丸直径;v0为初始0时刻撞击速度。图1中Wp、Wt分别为弹丸和靶板内的冲击波速度,α为撞击点位置角。
Ang[21]认为只要撞击点移动速度大于当前状态冲击波速,就不会产生稀疏波,也就不会产生反向溅射碎片。综合接触点速度及撞击后时长,得图2所示撞击点速度与位置角度关系,并与冲击波速度比较,得出弹和靶各自产生稀疏波的位置角(αjet,p,αjet,t),反向溅射碎片将由更小位置角的材料产生。在碎片云实验中,反向溅射碎片一般由薄板产生,假设弹和靶同种材料,参照图2将由靶材产生溅射碎片,符合实验结果。此研究不仅解答了反向溅射碎片的产生条件,而且揭示了侧向稀疏波产生前球形弹丸撞击靶板的物理过程。进一步,针对侧向稀疏波产生后过程,Wen等[22]提出了描述冲击波首次遍历整个弹丸过程中波阵面几何传播特征的几何传播模型(GPM),并分析了冲击波强度和速度衰减。上述研究基本完成了弹丸内的冲击波传播分析,但仍未能涉及到真正导致材料破碎的稀疏波传播及特征变化,无法借助材料动态破碎研究分析碎片的形成过程。
Grady等[23]提出了图3所示球形弹丸撞击薄板后轴线上压力时间历程的理论模型,将整个压力载荷分为2个主要阶段:第1阶段即为Ang[21]所分析的稀疏波开始产生前,压力值保持为初始撞击所产生的压力ph,可通过冲击波理论计算出;第2阶段则是来自弹丸侧表面的侧向稀疏波作用后压力下降至pb,可基于Bernoulli压力来大致描述pb大小。从时间上来看,第1阶段时长τ1由侧向稀疏波到达时间决定,而第2阶段终止时间τ2则是由来自弹丸尾端或薄板背面的轴向稀疏波到达时间决定。当薄板厚度和弹径比t/D较大时,压力时间历程即为图3所示,较小时τ2甚至可能小于τ1.但是,该模型中pb大小的确定缺乏理论依据,球形弹丸中侧向稀疏波的产生、传播以及弹丸尾端稀疏波强度都缺乏强有力的分析结论。模型中压力值只有2个状态,与数值模拟得到的连续下降过程不符,事实上目前缺乏此下降过程机理认知。
利用压力时间历程可计算冲击波所携带的能量,推算弹丸的破碎程度等,对碎片云侵彻性能有深刻影响。侯明强等[24]分析了密度梯度薄板和弹丸撞击过程压力时间曲线,发现薄板最前面的高波阻抗材料可提高初始压力,而后续材料的密度梯度使得冲击波慢慢卸载,增大了冲击波压力持续时间,弹丸破碎效果更好,可参照此流程思路对工程设计的结构和材料进行优化。此外,研究发现撞击速度较高时材料可压缩性会增大撞击界面压力,即使是弹靶材料的可压缩性相当[25-28],未来研究中也可能要考虑这一因素对碎片云破碎和相变效果的影响。
碎片云研究中,超高速撞击实验不可或缺。闪光X射线照相技术利用X射线照射碎片云,由于二维图像中碎片材料面密度分布不均匀,从而显示出不同灰度,沿弹丸速度方向多次闪光可获得碎片云扩散的多个图像。Piekutowski[29]借助闪光X射线照相获得了大量高质量碎片云照片,并研究了弹丸初始破裂阈值速度vs与板厚的关系[30],如图4所示。当t/D大于0.16~0.17后,阈值速度将保持恒定,这一现象被解释为板厚大于某个值后轴向稀疏波来不及追赶卸载弹丸内冲击波。在钢弹丸撞击聚甲基丙烯酸甲酯(PMMA)薄板实验[19]和轧制均质装甲(RHA)与钨合金弹丸撞击RHA薄板数值模拟[31]中也发现了类似规律。结合此现象考虑航天器防护,只有当板厚大于某个值时,才能保证冲击波遍历全弹丸,否则将产生大碎块,严重威胁航天器安全,相关理论计算可参考文献[32]。此外,轴向稀疏波追赶卸载冲击波对碎片云特性影响很大,但缺乏球形弹丸内此过程的基本分析,包括将导致的冲击波衰减量,以及与侧向稀疏波追赶卸载的竞争关系等。
进一步考虑弹丸破裂速度阈值问题,当t/D>0.16时,阈值速度为2.6 km/s不变。由铝合金材料参数得撞击点初始压力峰值为24.8 GPa,已有实验给出铝合金断裂应力为2.5 GPa,意味着侧向稀疏波将弹丸轴线压力峰值降低了22.3 GPa[20].当t/D<0.16时,这一压力降低值[20]近似为
Δp=8.57(t/D)-0.5.
(2)
若能获得确定工况下该压力的降低值,即可计算弹丸尾端轴向稀疏波的初始强度,进而分析材料破碎结果。然而由于缺乏冲击波衰减过程的分析,此压力降公式未能推广到非初始破裂工况下。另外,不论初始破裂阈值速度还是压力降低值,均可发现t/D与其非线性负相关,同时薄板厚度主要影响前述追赶卸载的发生时间。然而,球形弹丸中追赶卸载影响碎片云特性的机理未知。
图5为球形弹丸初始破裂后的变形情况示意图和实验照片。由图5可见,弹丸背面在稀疏波作用下鼓起,且与主体分离的部分厚度基本一致,这一现象印证了前文的形成机理分析,说明冲击波到达弹丸背面时近似球面,与后文中球形弹丸碎片云后部呈半球状的现象完全对应。
不论圆柱形还是球形弹体,均是对真实空间碎片的模拟,然而卫星解体实验发现立方体和方形片状碎片最多[33],且研究表明球形弹体毁伤能力低于非球形[34-35]。在圆柱形和球形弹体之外,张伟等[36]、马文来等[37]分析了椭球和方形弹体内不同位置处的压力历程,比较了压力峰值和材料断裂强度以判断弹丸破碎的情况。不过,弹体形状对碎片云影响的研究多为示例性比较,可用于分析特定形状弹丸导致的冲击波衰减过程差别,直接推测弹丸破碎结果差异。
1.3 薄板弹孔研究
薄板被弹丸超高速撞击贯穿后,撞击位置附近势必留下弹孔,在工程背景下被撞击的薄板实为航天器防护结构或舱壁,其损伤程度自然需要监测。目前有基于声发射信号[38]、光纤传感器[39]和电阻栅格[40]的测试方法被提出,可实现在轨航天器损伤感知、定位及损伤程度测定等。
图6为球形弹丸撞击不同厚度薄板所产生的弹孔,图中左边分别为孔洞箭头处切面,弹孔随着板厚的增加而增大,轮廓偏离标准圆形,且边缘情况更复杂[30]。图7为弹丸和薄板材料在碎片云中的分布情况,图中弹孔位置材料共有4部分:被弹丸冲塞部分、反向溅射部分、碎片云外围部分、小翻唇部分。已有研究认为弹孔形成分为两个阶段:先期冲塞和后期不断剥离,弹孔边缘留存则是剥离剩余材料。Piekutowski[30]定性分析了弹孔形成过程,即波系在薄板内的作用过程,认为弹孔边缘形状是由薄板两侧自由表面反射的稀疏波后拉伸所致,两列稀疏波在板中间相遇、产生层裂,导致小翻唇和锲形内环。从图6可见,随着板厚的增加,薄板从完全挤压成小翻唇到中间撕裂变形,两表面稀疏波造成的形变越来越弱,但更大的厚度意味着更复杂的相互作用,材料形变亦更复杂。弹孔材料后期剥离阶段导致弹孔边缘出现大颗粒块、空洞、裂缝等,形成机理与前文中的弹丸破碎相近。
后期剥离阶段弹孔大小的变化可参考文献[42]中的实验记录,弹孔首先快速增大,同时增速慢慢降低,直到弹孔大小稳定。以6061-T6铝合金材料薄板在7 km/s速度下被撞击为例,整个弹孔增大过程约耗时3 μs. 薄板弹孔与碎片云主体部分形成并不同步,一般弹孔形成更慢,不过弹孔后期扩大所形成的碎片云外围部分轴向速度较低,工程研究中基本可忽略。综上所述,目前已有弹孔形成过程的认识,但缺乏机理分析,两阶段对弹孔大小的贡献和对碎片云分布的影响均不明确,特别是薄板背面稀疏波所破碎材料的量无法确定。
弹孔大小方面,有基于能量的理论计算方法被提出[43],但主要针对中厚靶临界穿透情况且撞击速度较低,实际使用的以经验公式为主。柱形弹丸只需多考虑弹的轴向长度影响,与球形弹丸思路基本相同,不再进行专门分析。需要说明的是,弹孔各截面处直径不等,后文中弹孔大小为被贯穿孔洞的最小孔径,或不区分各处直径大小的差别。
在20世纪60年代,Maiden等[44]提出球形弹体撞击薄板的弹孔大小经验公式为
(3)
式中:Dh为弹孔大小;ct为薄板靶内稀疏波速。可见,弹孔大小与撞击速度、弹径及薄板厚度相关,特别是与撞击速度线性相关。同时,(3)式无量纲化各变量,具有更好的代表意义,而且通过引入稀疏波速考虑了薄板强度影响。此后,有很多研究者对(3)式进行了扩展和完善,如Sorenson[45]考虑了薄板剪切强度影响,Swale[46]考虑了弹和薄板密度影响,Schonberg[47]引入了入射速度角,Hill[48]引入了弹强度项。
综合而言,此类弹孔大小的经验或半经验公式形式为
(4)
式中:ρp、ρt分别为弹和薄板材料密度;cp为弹内稀疏波速;θ为入射速度与薄板正面内法向夹角;C1、C2为常数参数[49]。Abbas等[49]通过机器学习遗传算法给出(4)式中参数pi(i=1~5)的一组取值为p1=0.08、p2=0.62、p3=0.03、p4=0.88、p5=-0.08,可以看出v0/ct项和t/D项影响较大。对于确定弹径的弹丸情况,弹孔随着撞击速度和板厚的增加以及靶板强度的降低而增大。除(4)式外,亦有其他形式的公式被提出[50-52],特别是Rolsten等[50]曾提出基于一种冲击模型的理论公式,但弹孔大小这一主要影响因素的分析结论未改变。
除上述公式外,Loft等[53]分析了弹丸绕速度方向自转对弹孔大小的影响;Piekutowski等[41,54-55]通过实验研究发现弹孔大小强依赖于薄板的强度,但增大速度随t/D的增大变化很小,另外当t/D较小时撞击速度对弹孔大小的影响小,较大时影响明显;Myers等[56]通过实验研究发现高温状况下靶板将产生比室温下更大的弹孔。
综上所述,弹孔大小的影响因素和计算公式已较完备,目前缺乏复杂环境及极端工况下弹孔的表现。对弹孔形成机理和弹孔大小的理论分析工作很欠缺,相比于碎片云,弹孔易于实验观测,或可由此入手推测碎片云的形成机理。另外,弹孔大小直接决定了薄板对碎片云的质量贡献等,对碎片云分布的建模需要更细致的弹孔形成研究结论。
近年来,有一些新型薄板材料被提出,如一种自修复离聚物[57],其弹孔相比于传统铝合金材料更小,可降低薄板的损伤程度,且薄板碎片云危害很低,但其对弹丸的破碎效果较差,难以满足工程需求。薄板材料的选择工程意义明显,从常见的铝合金材料到编织材料再到功能复合材料,未来必将是更具针对性的智能化材料。事实上,可借助碎片云形成过程的研究结论,掌握板材选择到改进工艺的整体研究方向。
2 碎片云分布特性研究
碎片云分布研究既可验证碎片云形成过程的推算结果,更可为碎片云模型建立提供基础。然而由于实验测量难度大,所取得的成果很有限,数值模拟被广泛应用,理论研究方面进展缓慢。本节将阐述碎片云外形及构成和碎片云速度、质量及相态分布,其中碎片形状、大小及材料动态破坏模型等包含在质量分布中。
2.1 碎片云外形及构成
2.1.1 碎片云外形研究
弹丸和薄板在稀疏波作用下破碎后形成碎片云,大部分材料继续沿入射方向运动并径向扩散。图8为直径9.53 mm的2017-T4铝合金球撞击1.549 mm厚6061-T6铝合金薄板所形成的碎片云,速度方向自左向右。右边部分为碎片云长时间扩散后的图像,可见碎片云最前端的细节结构,边缘拟合算法识别显示球形弹丸碎片云前端接近抛物线[59]。图像颜色深度与碎片分布密集程度呈正相关,前端狭带颜色最深部分即碎片分布最密集部位,但目前尚无碎片分布密度的定量测量方法。
弹丸形状影响波系作用过程及稀疏波到达时间,导致不同碎片云外形,图9为等质量球形弹丸和不同长径比圆柱弹体撞击薄板所产生的碎片云图像,图中l为弹体长度。由图9可见,球形弹丸碎片云前端接近旋转抛物面,柱形弹丸碎片云前端不圆滑,最前端为三角锥形。通过长径比分别为0.06(圆盘)、1.00(正圆柱体)、3.55(短棒)3种圆柱体撞击薄板的实验发现:短棒弹体碎片云主体为“茶杯托”状,尾部较平直,约1/2的弹体保持完整,与碎片云主体一起向前运动;正圆柱体弹体碎片云主体尾端尚有小的突出部分;圆盘弹丸碎片云内部为长柱体,贯穿整个碎片云薄板后部分,且在运动中变长但径向不扩散,碎片云最前端也近似圆柱体而非三角锥形[60]。由此可见不同弹体所产生碎片云外形和结构的差别导致其侵彻性能差异很大。靶板结构影响亦被考虑,如铝网[61]和蜂窝夹层板[62],有数值模拟结果可参考。弹靶材料、结构、形状均可能改变碎片云形状,同时意味着侵彻性能变化,目前的研究考察范围不足。
圆柱形弹丸可能自身姿态偏斜,以一定俯仰角垂直撞击薄板,碎片云不再沿速度方向对称。图10和图11分别为圆柱弹体无俯仰角和有俯仰角时的碎片云及特征模型。无俯仰角时碎片云内核部分近似两个底面重合的圆锥体,外围部分为与球形弹丸碎片云相近的椭球形;有俯仰角时碎片云内核出现了明显的偏斜,与外泡结合部位发生了变化[63]。非球形弹丸均存在撞击姿态问题,太空中真实的空间碎片弹体轴向和速度方向很可能存在俯仰角,但弹体姿态对碎片云影响缺乏分析,特别是针对碎片云速度和质量分布。
除前述圆柱形弹体和球形弹丸碎片云外,国内学者还分析了椭球形、方形、锥形等形状弹体碎片云[36-37,64],主要基于数值模拟方法,分析碎片云外形及特征速度差异。然而,目前的研究工作尚不能解释不同形状弹丸引起碎片云外形差异的原因,如正圆柱体弹碎片云尖端为何为三角锥形。碎片云形成的共性基础研究尚缺乏,无法拓展分析具体形状弹体或弹体的俯仰角问题。
2.1.2 碎片云内部结构研究
针对球形弹丸碎片云,Piekutowski[58]通过细致观察碎片云图像提出图12所示的结构分解,将整个碎片云分为反向溅射流、外泡和内核结构3部分,其中内核结构又可分解为前、中、后3个区域。内核结构通常被视为碎片云的主体部分,由图12中的颜色深度可知内核结构前端和中部碎片最密集,这两部分对后续靶板威胁最大。内核部分的3个分区很可能是不同稀疏波的作用过程导致,可由此针对性地优化薄板材料和结构,降低前段和中部材料分数。
关于碎片云中的材料分布,Rosenblatt等[65]曾用数值模拟方法提出另一个模型,但就内核结构部分而言图7的描述更可靠。
前文中碎片云图像皆为侧视图,目前实验中通过闪光X射线照相、光学高速摄影[66]和激光阴影照相[67]等从某个侧面拍摄碎片云,将三维空间分布投影到二维,势必导致投影方向信息叠加,难以准确表明碎片云的空间分布。Swift等[68]通过在碎片云轨迹上设置网格将碎片分区,定量描述了球形弹丸碎片云的速度、质量及材料分布,发现碎片云实际上是空壳结构,并认为几乎所有碎片均分布在一层薄壳上。Piekutowski[20]通过挡板和狭缝(见图13(a))得到碎片云薄层(见图13(b)),发现球形弹丸碎片云内核实际上有前后两层,箭头所指部分为内核前端,大阴影区域为内核中部。圆盘弹丸碎片云也有类似实验,如图14所示。该实验由铜圆盘撞击铝薄板,铜在X光下的透光度远差于铝,可明显区分弹丸碎片云和薄板碎片云,其中箭头所指为薄板碎片云最前端[69]。图14中薄板碎片云和圆盘弹丸碎片云各自分布在一层薄壳上,但内核部分无类似球形弹丸碎片云的两层分布,目前尚不能明确解释图14中的结构形成机理,亦缺乏铝圆盘实验作为对比。此外,其他t/D及撞击速度下上述分层结构变化规律未知。
分解内核结构发现,内核中部中心部位存在单个中心大碎片,如图15(b)和图15(c)所示,这一发现为建立碎片云模型提供了思路,已有以该大碎片为主体的碎片云工程侵彻模型被提出[70]。实验发现,随着t/D或弹速的增大,中心大碎块尺寸减小,其速度随着t/D的增大而减小[20]。
实验发现,随着t/D的增大,内核中部和后端形状基本不变但尺寸快速增大,前端外形会出现明显差异,在t/D=0.16附近内核前端由图12所示“塞子”状无尖圆椎体变为图13所示抛物线形。随着弹速的增加,内核结构尺寸快速扩大,但形状基本不变[58]。内核结构的外形和尺寸均由碎片速度分布决定,上述变化机理的研究实际上归结于速度分布的研究。
前文提到Ang[21]解释了弹和薄板接触面稀疏波产生的位置和条件,意味着侧向稀疏波产生前的冲击波为准一维等强度波。Piekutowski[58]利用Ang理论解释了碎片云内核前端结构特征,如图16所示,提出碎片云内核前端部分实际上是侧向稀疏波产生前的准一维冲击波影响区域,在薄板背面转变为稀疏波后导致了内核前端部分的剥离。以直径9.53 mm的2017-T4铝合金弹丸6.67 km/s撞击薄板为例,弹丸中该准一维冲击波作用区域大小为弹径的56%;由回归计算图16中的碎片云前端部分得出,0.12 μs时前端部分大小也约为弹径的56%[58]. 此外,在该准一维等强度波作用下,内核前端部分破碎后获得的速度值很接近,因此呈现出图13所示碎片分布密集的内核前端部分。
图14中圆盘弹体碎片云尾端并非前文预测的平面结构,原因有二:1)弹体俯仰角导致面撞击变为点撞击,破坏了理想平面波,在数值模拟中理想平面结构会更明显;2)侧向稀疏波的衰减使冲击波阵面从径向外围开始逐渐由平面变为凸面,弹体轴向尺寸较大时尾端平面结构将完全消失。球形弹丸碎片云内核后端为半球状,符合前文预测,但来自弹和薄板背面的稀疏波均已在破裂材料过程中衰减,导致内核中端产生大碎片且速度差异不足而碎片聚集,同时可预测出由于板厚的影响,中心大碎片材料来自原弹丸中心的稍前位置。由碎片云外形结构可验证前文所述碎片云的形成过程认识基本无误,可通过数值模拟获得丰富且具体的数据反推碎片云形成过程。
2.2 碎片云速度分布
碎片云实际上是大量小碎片的集合,每个碎片具有独立的运动速度矢量以及后文将分析的质量、大小、形状和相态,这些状态量在宏观上表现为数学分布。碎片速度包括轴向速度和径向膨胀速度,研究中多关注撞击速度和t/D等参数对碎片云速度分布影响。
碎片云中不同位置处碎片速度的分布已有数值和实验的研究[68,71],但无法数学化描述其分布规律,只能看出碎片速度及其与轴线之间的夹角不符合线性规律。更多的研究中描述了碎片云结构特征点速度变化,或简化的碎片云模型特征速度。
碎片云内核结构外形随撞击参数的改变而变化,Piekutowski[58]测量了特征点速度变化情况,但未借此解释碎片云结构变化。图17为节选的部分特征点无量纲速度曲线,简单展示了碎片云速度分布和结构变化关联,其中⑤-⑥形式表示两点间径向速度vrad. 当t/D较小时,①、⑤、⑥点轴向速度va基本一致,因此碎片云内核呈现塞子状前端。随着t/D的增大,①点速度降低快于②点,以及⑤、⑥点速度增速大于⑦、⑧点,导致轴向塞子逐渐凸起,侧边界不断圆滑,内核前端变为抛物线形。随着撞击速度的增大,靠前特征点速度增速大于靠后的,因此内核结构表现为尺寸变大但形状不变。撞击速度增大时碎片云内核结构轴向膨胀可通过①点和④点速度差解释。
此外,⑦-⑧点径向速度在t/D=0.16附近出现极大值的机理未知[58],或可考虑Ang分析理论[21]中稀疏波开始产生时轴向冲击波在薄板中到达的位置,若t/D过小,则薄板反射的轴向稀疏波可能影响到⑦-⑧点的径向速度。
内核后端半球形碎片区域的膨胀速度随着t/D和撞击速度的增大而增大。考虑前文弹丸初始破裂速度在t/D=0.16附近出现拐点,膨胀速度在此临界处似乎存在极大值,被解释为随着板厚的增大,轴向稀疏波更晚卸载弹丸内的冲击波[58]。考虑1.1节的侧向和轴向稀疏波竞争卸载冲击波,当板厚接近临界值时,轴向稀疏波的影响程度会慢慢弱于侧向稀疏波,从而出现极大值。板厚影响胜于撞击速度,认为是冲击波脉冲时长对后端膨胀速度的影响甚于冲击波强度[20],但缺乏解释。
碎片云建模中利用速度和外形耦合来建立表达式,但目前对特征速度数据的利用和分析不足,对从稀疏波作用到碎片速度分布过程的分析不足,只是单纯的数据测量。
除t/D和撞击速度外,实验发现不同弹丸材料下碎片云内核后端膨胀速度和中部轴向速度会有所差异[20],汪庆桃等[72]通过数值模拟研究了铝合金、RHA和钨合金弹丸碎片云特征速度变化情况,并提供了经验公式,但均未能说明相应的变化机理。
理论研究方面,Kipp等[73]分析了碎片云径向膨胀速度,不过其关注点主要在材料动态破坏,多选用板厚大、撞击速度低的圆盘状碎片云(见图18(b)),且实验材料在航天器防护工程背景下所代表的意义不大。基于侧向稀疏波产生后将追赶卸载冲击波的现象,Kipp等[73]利用Ang分析理论[21]计算了冲击波脉冲时长,结合冲击波基础理论得到冲击波所携带能量;扣除热耗散和轴向速度占用的能量,利用动能原理计算径向速度的大小;进一步考虑了破碎新表面能和断裂应变能的影响,所得到的理论径向速度与实验值相当接近,如图18(a)所示。该分析所选用的碎片云虽然不同于本文主要论述的碎片云,但其建模思想参考价值很大,特别是对能量损耗的分析,在以后的碎片云速度和质量分布研究中不可或缺。
膨胀半角被定义为最外侧碎片速度矢量与轴线的夹角,决定着碎片云的扩散范围。数值模拟发现其随撞击速度的增大而增大,随着t/D的增大而减小[72],变化规律可参考文献[71]。该角度与侧向稀疏波强度关联紧密,其变化有助于形成过程分析。
综上所述,碎片云外形及结构实际上由速度分布决定,但目前难以描述碎片云的整体速度分布,只有某些工况下特征位置速度随撞击速度和t/D的变化规律及一些经验公式。未来研究中,要尝试定量描述碎片云的整体速度分布,如连续的碎片云外边界速度分布表达式;还要关注物理过程和机理认识,建立从稀疏波导致材料破碎到速度分布以及碎片云外形、结构等变化的关系。
国内关于碎片云速度分布的研究大多基于数值模拟方法,关注撞击速度、弹和薄板尺寸等对碎片云特征位置和速度的影响,并尝试建立经验公式。碎片云问题数值方法目前通用为光滑粒子流体动力学(SPH)方法,本质上是一种无网格Lagrange算法[74-75]。国内研究者大多使用有限元分析软件AUTODYN或LS-DYNA内的SPH模块[76-77],亦有研究者自主编写SPH算法程序,如李毅等开发的PTS并行计算软件[78]。数值模拟中状态方程、强度模型等材料模型会对计算结果产生影响[79-81],但目前考察的撞击工况范围不足。
实验中碎片云外围尘埃尺寸过小,在图像中不会呈现,但由于计算资源限制,SPH方法中填充粒子尺寸大于尘埃。边界处孤立粒子的飞散,导致碎片云总体动量和能量分配不准确,带来计算误差。同时,无法确定碎片云结构边缘,计算和实验结果难以对比,特别是速度特征点的确定。Zhang等[82]提出在计算模型中布置测量点并分析其运动状态,可准确获得计算结果中的碎片云结构和特征点位置,降低数值模拟后的处理误差。然而,这种手段较为麻烦,且人工分析过程缺乏定量标准。SPH方法在此方面需要优化算法以减小计算资源消耗,进而采用更小更多的粒子填充,并尝试用非均匀大小的粒子填充,以保证关键区域的计算精度。
国内研究中大多假设碎片云结构为球形,只采用轴向质心速度和径向膨胀速度两个值来描述碎片云的速度分布,在更广泛的撞击参数和条件下,分析前述实验规律的适用性。速度分布方面,张永强等[83]提出撞击速度增加所带来的弹动能增加量更多地分配到了径向膨胀速度方面,而弹径增大带来的弹动能增加量则更多地分配到了轴向质心速度方面,板厚增大后质心和径向速度均降低但质心速度降低更快。此结论应用价值较大,但缺乏深层次的分析。
2.3 碎片云质量分布
超高速撞击后弹和薄板弹孔部分破碎为小碎片,每个碎片具有不同的形状和大小。碎片质量对其侵彻性能影响明显,形状和撞击姿态也会影响后续靶板的破坏程度。
2.3.1 Grady材料动态破碎准则
碎片大小方面,Grady[84]基于能量平衡研究了材料的动态破坏,将材料单元动能分为整体动能和局部动能,整体动能在材料破坏过程中保持不变,仅局部动能和材料的弹性应变能参与动态破碎。断裂过程中,形成新表面需消耗能量,即破碎新表面能,Grady提出只要材料局部动能和弹性应变能能够提供产生新表面所需的能量,便可发生破碎。基于此能量平衡,利用能量最低原理,得到断裂所需断裂强度、断裂耗时、碎片尺寸等,但与实验对比发现脆性断裂吻合较好,韧性断裂误差很大。之后,Grady[85]又基于断裂耗时最短假设重新求解了能量平衡关系,得到了(5)式,与低撞击速度下的韧性断裂实验结果吻合很好。
(5)
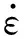
在此基础上,Grady[85]针对不同应变率下材料不同的断裂状态,提出了3种破坏机理模式:低应变率下脆性断裂,由断裂强度主导;中应变率下韧性断裂,由屈服应力主导;高应变率下液体断裂,由表面张力主导,很好地完善了破碎准则理论。
碎片云问题中,撞击压力远大于破碎断裂张力时,张力达到断裂阈值所需时间会小于断裂耗时,因此断裂耗时最短假设应修改为基于断裂张力,这才是强撞击下的主要影响因素[86]。Yew等[86]将(5)式中的断裂张力Ps用峰值张力Pm取代,得到新的断裂耗时和碎片尺寸表达式:
(6)
式中:γ为液体表面能,是关于温度的函数。此时只需要获得材料内部Pm的分布即可计算碎片的尺寸分布。同时,Yew等[86]提出(5)式和(6)式都假设撞击产生的全部或大部分能量用于破碎过程,但实际上只有小部分,实验也证明计算的碎片尺寸偏小,因此又提出等效断裂强度Pe:
(7)
式中:Kc为材料断裂韧性;R为材料处于Pm张力状态下时的特征尺寸。以Grady破碎准则为基础的这一系列碎片大小和断裂强度判断公式已被广泛应用于碎片云研究中,AUTODYN软件也已将Grady破碎准则引入作为标准失效准则之一[87]。
这一系列准则从能量角度入手,计算碎片尺寸特征,碎片云理论分析只要得到稀疏波强度,假设出合适的应变率,即可计算碎片尺寸。更进一步,按上述准则参数计算单个碎片尺寸,即可获得此处稀疏波的衰减量,重复此过程,可获得完整的碎片云分布数据。出于实际可折中前述两种,根据碎片尺寸分布差异分区后计算区域平均尺寸,获得近似碎片云整体尺寸分布。
在数值模拟中,SPH算法得到的碎片云其整体分布规律与实验结果接近,但单个尺寸尺度的可靠性不足。一方面,由于实验材料本身缺陷和不均匀较随机,无法拟合;另一方面,模拟采用的Grady破碎准则本就是基于统计意义,无法保证单个碎片规模的准确性。同时,可在失效模型中引入随机扰动,如AUTODYN 中基于Mott分布[88]的碎片随机失效方案。
2.3.2 碎片云质量分布规律研究
球形弹丸碎片云图像碎片识别处理发现,内核中部碎片随着t/D的增加,碎片形状依次呈现薄片状、“逗号”形和短粗状;内核后端半球内碎片在板厚和弹速较低时为薄片状,弹速增加后为短粗状;前文提到的大中心碎块随着t/D和弹速的增加由短粗状变为圆盘状[20]。由此,Piekutowski[20]认为内核中部碎片由冲击波压缩时的剪切作用产生,与张庆明等[16]的分析吻合。碎片形状的测量难度大,同时缺乏碎片形状对侵彻性能等影响的分析。
Akahoshi等[89]以聚乙烯柱形弹丸撞击铝合金靶板,利用阻尼材料收集靶板材料部分碎片,并测量碎片位置和质量等,得到碎片质量和数量分布规律:
lg (CN)=a-b[lg (mf/me)+c]2,
(8)
式中:CN为碎片累计数量;mf为收集的碎片质量;me为所有碎片的总质量;a、b、c为拟合常数。
图19为3.4 km/s速度下撞击产生的碎片质量分布,其中曲线参数为a=16.1、b=0.47、c=3.79,可见质量分布基本符合(9)式所示的抛物线。在弹和薄板均为铝合金的球形弹丸实验中,碎片质量分布也基本符合抛物线[90]。此外还有其他形式的公式被提出,如Grady等[91]的线性指数分布、双线性指数分布,亦能很好地拟合实验结果。
Nishida等[92]在碳纤维加强塑料(CFRP)薄板前后设置验证板,收集了薄板正向和反向溅射的边缘区域碎片,并与NASA破碎模型[93]比较,发现正向溅射边缘区域碎片尺寸分布不依赖于撞击速度。但是,上述系列实验的撞击速度均较低,在典型碎片云撞击速度下的适用性未知。
提高撞击速度或增大t/D均可使碎片更细小,由(7)式也可发现压力峰值越大,碎片尺寸越小。提高撞击速度可直接增大压力峰值,而增大t/D会增加强冲击波时间脉宽,导致强压作用区域更大,产生更多小碎片。然而,理论计算目前仅有碎片平均尺寸,以及中心大碎片等大质量碎片的存在,实验和理论结果难以对比。
Piekutowski[20]实验发现随着撞击速度的增加,中心大碎片尺寸和内核后端碎片平均尺寸按撞击速度的幂次方减小,而t/D的改变不影响该幂次关系,只改变碎片尺寸,提出的拟合公式为
(9)
(10)
式中:df为中心大碎片尺寸(球等效尺寸);dm为半球形后端内碎片平均尺寸(Martin统计直径等效,对数平均化方法[20])。将实验值dm和(5)式计算结果对比可知,计算值比实验值大2倍;而内核中部中心大碎片周边碎片平均尺寸实验值比计算值大1.5~2.0倍。可见,实验结果的整体均值应当与Grady准则计算值接近,但计算值无法表达不同区域的碎片尺寸差异。
上述实验中侧面拍摄图像存在重叠投影,碎片径向尺寸可能不准确。迟润强[94]利用观察板弹孔直径回归计算碎片尺寸,获得了中心大碎片球等效直径,何茂坚[95]对此数据进行了简要分析。但是,此系列实验数据撞击速度均在5.5 km/s以下,而Piekutowski实验中不乏6~7 km/s撞击速度,相变问题或影响二者的实验数据吻合度,测量方案的不同也必然带来差异。
形成机理方面,柳森等[96]利用石蜡板收集实验碎片,比较不同速度下碎片云的尺寸分布,得出结论:小碎片主要由高应变率冲击和相变影响形成;大碎片则由较低应变率冲击下材料沿薄弱处撕裂脱落而成。关于碎片尺寸的实验数据很缺乏,而且现有方法均不够精准;理论工作则需要对材料破碎难题的研究,以及对Grady破碎准则的进一步利用。
理论建模中通常由碎片云中的材料质量和密度计算碎片总体积,结合碎片平均尺寸得到碎片数量,但由于碎片形状不规则及内部空隙等影响,等效的碎片体密度一般小于原始材料密度。实验发现,碎片云内核后端的碎片数量正比于撞击速度的幂次方;随着t/D的增大碎片数量增大,可通过板厚增大导致了弹孔部分材料体积增大来解释[20]。同时,必须分别考虑不同尺寸碎片的数量变化,如t/D的增加主要增多小碎片,而大尺寸碎片甚至减少[81]。
2.3.3 SPH模拟碎片识别方法
SPH方法中可设置观测点,便捷地获得碎片云速度和相态分布,但难以统计质量分布。SPH方法采用离散粒子填充计算域,粒子之间没有类似网格的关联,得到的计算结果不具备连续性,仅提供粒子点坐标等,需要专门识别碎片以确定哪些粒子属于同一碎片。
1995年Benz等[97]针对脆性材料断裂,提出基于累计损伤因子的边界识别方法,即断裂位置处粒子构成碎片边界。徐金中等[98-99]考虑到碎片云问题中高温高压导致的材料相变等,提出采用“自然边界”来识别碎片更为合理,利用“近邻的近邻”搜索方法,当发现由于碎片间距离增大而某些粒子在某方向上搜索不到近邻粒子时,视为碎片边界。以上两种方法均基于碎片边界识别碎片,另一种思路则是基于粒子间距直接判断碎片所含粒子,然而直接判断算法复杂度很高,需要附加技巧。
Zhang等[100]提出有限元和粒子法结合的FEM-SPH-FEM方法,先利用有限元(FEM)建模,再转为SPH进行计算,而后将计算结果转到FEM进行碎片识别。之后将FEM碎片云转为二值图,利用连通域计算法统计碎片数目,最终给出大碎片特征长度、质量及速度分布信息。Liang等[101]利用子网格将粒子先构建为链表,而后在连通图中采用广度优先搜索算法确定粒子归属,最后构建碎片外凸壳,删除碎片内部粒子,得到大碎片边界及特征信息。上述方法有效地解决了SPH算法后处理难题,但也有改进空间,特别是基于粒子间距识别时间距大小的选择,缺乏力学依据。基于粒子间距的分类方法可扩展到更高维度,如利用粒子位置坐标、速度共6个维度数据分类,事实上机器学习方面已有聚类算法可对粒子更多属性度量相似性,非常适用于碎片识别。
AUTODYN软件内也集成了一种碎片识别方法,其基于边界识别思路,过滤掉单独存在的失效粒子,提供未失效的粒子群信息[35]。
基于碎片识别,徐金中等[98]研究了不同弹形和不同撞击速度下的碎片质量分布,发现速度相同时不同弹形碎片云的质量分布基本一致,同弹形不同速度下分布相似,但圆柱形弹丸的最大碎片明显大于球形和圆盘弹丸,影响碎片云的侵彻性能。另有基于AUTODYN碎片识别方法的模拟[81]显示,撞击速度增加、碎片总数增加,但基本不改变碎片云的质量分布规律;板厚增大、碎片总数显著增加,板厚直接改变强稀疏波作用区域的大小,比撞击速度只改变冲击波强度的效果显著。
碎片云质量实验测量技术困难,数值模拟方面大多停留在碎片云外形和速度方面。上述识别技术门槛较高,但前景很好,后续首先可考察算法准确性、材料模型选择等,而后弥补的实验欠缺关于质量分布规律的分析。同时,碎片识别方面研究应开始关注最大碎片等具体碎片,不再是宏观的碎片云统计特性。
2.4 碎片云相态分布
2.4.1 碎片材料相变机理及温度测量
超高速撞击可能导致材料发生相变,固相碎片保留了材料高强度而侵彻性能强,液相和气相的碎片侵彻能力远弱于固相。不过,即使是气相碎片,也能够给后续靶板施加强作用力,使其发生弯曲、层裂等[10]。关于材料相变原因等,Anderson[9]和张庆明[102]有过详细分析。
以2A12铝合金为例,其在撞击速度5 km/s左右开始熔化[102],在近9 km/s下碎片主要为液相和气相[103],说明实际空间碎片和航天器防护结构相撞后碎片云材料必已开始相变,甚至液相、气相为主。相变降低了侵彻性能,同时相变后只需要克服材料张力即可导致材料破碎,产生更细小的碎片。还有学者指出,冲击波导致的热软化和相变降低了碎片云平均动能,并降低了动能集中度[104]。
超高速撞击实验中,常规温度测量手段响应太慢,无法获得碎片云温度数据或材料相态分布。碎片材料在高撞击压力时发生相变,同时还可能出现等离子体,电离产生多个波段的电磁辐射现象,如闪光[105]、红外喷发[106]和无线电频段辐射[107]等。研究发现,等离子体在超高速撞击中容易产生,其电磁效应会对航天器电子设备产生电磁毁伤[108-109],而弹丸撞击速度以及弹和薄板的材料、尺寸等均会影响等离子体的电磁毁伤效果[110-111],设计防护结构时需要具体考虑。
另一方面,等离子体电磁辐射被用于碎片云温度实验测量。首先测量电磁辐射强度,然后主要有两种数据分析思路:一是将实验物体视为黑体,利用普朗克黑体辐射定律计算物体温度;二是根据原子分子辐射原理,分析实验得到的特征谱线,得到温度信息[112]。Ward等[105]参照第1种思路获得了碎片云温度,但发现实验值远高于CTH计算结果。马兆侠等[113]依照第2种思路,测量了实验中反向溅射碎片云区域250~340 nm波段电磁辐射,利用Boltzmann图解方法,获得了弹和薄板材料为纯铝时粒子云团温度和撞击参数关系:
(11)
式中:T为粒子云团温度。实验薄板厚0.2 cm. 此外,利用外形拟合方法也可获得温度数据,结果与Boltzmann图解法相近[114]。
除测量确定时刻的温度外,还可以借助时间分辨光谱获得撞击后温度随时间变化的情况[115-116],这些数据为数值模拟工作提供了校验参考。然而,此类实验多是平均意义温度,难以获得温度分布情况,而且辐射强度与温度计算方法不同,可能出现不同结果。
2.4.2 碎片云相态分布理论和数值模拟研究
由于相变对碎片云侵彻性能的影响,理论建模中需要考虑其分布。Schonberg[117]提出了基于能量的柱形弹丸材料相态计算方法,通过状态方程计算材料被稀疏波卸载后的剩余能量,与材料升温及发生相变所需热量值对比,得到材料所处相态。对于混合相情况,其利用线性化差值思路,即以剩余能量减去升温能量,差值除以相变潜能,得到两种相占比。张永强等[83]利用此方法计算了球形弹丸情况,发现被冲击波作用过的区域内材料相态分布与t/D无关,符合碎片升温机理。然而,Schonberg方法只能计算材料整体所处状态和各相占比,不能描述具体分布,这种类似平均化的思路也导致计算结果至多含有两相。
Piekutowski[118]针对球形弹丸提出了一种弹丸材料相态分布计算模型。首先根据冲击波理论计算初始撞击压力峰值,假设弹丸内压力峰值降低量Δp只与t/D有关,利用(2)式得到弹丸尾端压力峰值。为便于计算,其假设球形弹丸轴线上的压力峰值随距离线性降低,得到弹丸轴线上各位置的压力峰值;结合状态方程和粒子速度与材料压力的关系(见图20(a)),得到弹丸轴线相态分布。参照图20(b)所示,假设垂直轴线的截面相态一致,由轴线上的材料相态分布决定整个弹丸相态分布。在混合相区域,由所处位置到两侧单一相区域的距离线性插值处理,如在图20(b)混合相区域轴线靠右侧三等分点处,包含2/3的液相材料和1/3的固相材料[20]。该模型明显存在不合理的假设等,但提供了一种可行的材料相态分布计算方法;相比Schonberg的方法,该模型真正描述了材料相态分布。
由于实验发射能力有限,通用铝合金材料尚难气化,液化则可通过对验证板上的碎片做金相分析确认,还可利用液化碎片在运动中形状的改变作为证据[69]。目前,可实现镉、铅、锌等金属的冲击气化实验,图21为弹靶材料同为镉时碎片云气化后的新结构特征,气体材料的膨胀运动也导致碎片速度分布稍有变化。Schmidt等[119]曾利用镉气化实验类比铝合金材料气化后的情况,并由此推算铝合金材料碎片云侵彻的性能变化[20]。在低密度材料Mylar以14 km/s速度和中密度2A12铝合金以近9 km/s速度撞击2A12铝合金薄板的实验中发现,低密度材料下铝合金薄板未发生相变,而中密度材料下碎片云主要为液相和气相,材料参数对撞击压力的影响明显,进而影响相变情况[103]。
数值模拟便于计算材料相变,但缺乏定量实验数据来验证,可靠性未知,只能重现材料相态分布变化的基本趋势。由CTH软件计算发现,撞击速度10 km/s以上时,材料强度对相变影响可忽略,可采用初始压力峰值或者材料最终温度判断材料的相态;撞击速度为10 km/s以下时强度影响明显,建议用材料最终温度作为相态判据[120]。但是,材料温度计算结果依赖于状态方程,使用欧拉算法的计算已证实此问题[121],需要慎重考虑涉及材料相变时的材料模型适用性。
相比于常用状态方程,GRAY三相完全状态方程和SESAME完全状态方程数据库在冲击气化下较适用,在球形弹丸碎片云相态分布计算方面已有应用[122-123],如图22所示为在AUTODYN内嵌入SESAME数据库获得的球形弹丸碎片云不同时刻相态分布,其中撞击速度为15 km/s,材料均为铝。图22的计算图例中2.0代表完全气态,1.0代表完全液态,0代表完全固态。可见,碎片云中可能三相共存,图20(b)中的模型符合此变化规律,但其垂直截面同相态假设有较大差错,可参照球面设定,这样更符合球形弹丸内的冲击波形状。
综合来看,碎片云材料相变机理较简单,借助数值工具容易实现,但离不开状态方程,已有状态方程未考虑相变后情况,新型状态方程需要自主编程或二次开发方可使用,门槛不低。
3 碎片云模型研究
碎片云模型即对碎片云分布特性模型化,包括质量分布、速度分布、碎片位置等,更进一步还包括碎片相态。已有碎片云模型主要源于Swift模型或Piekutowski模型,后期将不断改进。考虑到郑建东等[5]已于2011年发表较详细的碎片云模型综述,本节将在该文基础上分析建模思路及补充个别新模型,不再细述模型具体内容。
3.1 Swift模型类
初期研究集中在分析动量和能量守恒[9],通过调整人工参数构造碎片云模型。Swift等[124-125]基于此思路提出了碎片云工程计算模型,用于航天器防护结构的设计评估。
如图23所示的Swift模型不区分弹和薄板碎片,假设整个碎片云为质量均匀分布的球壳。速度矢量分解为质心平动速度和径向膨胀速度,质心速度基于动量守恒,以弹孔大小计算碎片云中的薄板材料质量;径向速度利用能量守恒,将弹丸动能分解为平动动能、膨胀动能、材料碎化及相变消耗3部分,引入参数表示单位质量材料碎化及相变耗能,并根据具体破坏情况调整参数值。然而,该模型中的质量均匀分布假设被质疑,与大部分质量集中在碎片云薄壳前端中轴线附近的实验现象不符[126],模型中碎片云粒子的疏密程度也与实验不符[127]。图23中,ds为弹孔直径,vf、vr、vi和ve分别为弹丸碎片云的头部速度、尾端速度、质心速度和膨胀速度。
从建模思路来看,模型分为3部分:外形、质量分布和碎片运动,外形为单层球壳,质量采取均匀分布,运动方面用两个速度矢量叠加实现,速度计算基于常规的动量和能量守恒,可视为是最简单的完整模型。此模型过于简化,且当时普遍认为碎片云是完全中空的一层壳,导致模型的计算结果偏差大。后续模型改进了Swift模型对碎片云的描述,建模思路基本不变。Nebolsine等[128]提出的针对径向较小尺寸薄板的碎片云模型,与Swift模型非常相似,可进一步参考。
1999年Schonberg等[129]提出如图24所示的弹和薄板碎片云分离模型,其假设薄板碎片均匀分布于外层球壳,而弹丸碎片均匀分布于内部实心球体,二者在头部相切,更接近实验事实。质量分布方面,弹和薄板碎片仍都是均匀分布。运动速度沿袭Swift模型的叠加方案,不过此时外球壳和内部球体各有两个速度矢量,利用相切关系得到二者头部速度相等,并假设弹丸碎片云径向速度vpr和薄板碎片云径向速度vtr之比为它们质量的反比,求解碎片云运动速度。Schonberg模型的主要改进点在于碎片云外形,将弹和薄板的碎片云分离,但增加了径向速度与质量呈反比假设。张永等[130]在Schonberg模型基础上,假设弹和薄板碎片云相对各自中心膨胀速率与半径呈线性关系,并借此考察碎片云撞击后墙的载荷分布,及改变弹丸直径和撞击速度后的载荷变化情况。图24中vpa、vta分别为弹丸碎片云和薄板碎片云的轴向速度。
2001年Corvonato等[131]基于碎片云扩散过程中的外形自相似,参考碎片云SPH算法模拟结果,建立了包含反向溅射碎片的完整球形弹丸碎片云模型。碎片云外形分内外两层,薄板碎片分布在外层壳,弹丸碎片则分布于内层附近,利用Bernoulli双纽线描述外形。质量分布基于面密度和极坐标系,薄板碎片在角坐标上呈Gauss分布,弹丸碎片在角坐标上呈线性分布、径向坐标上呈Gauss分布。模型虽遵守质量、动量、能量守恒,但运动速度关键量均来自数值模拟结果经验公式,导致模型依赖于数值结果且计算复杂。蒋彩霞[132]、迟润强[94]先后修改了此模型碎片云的外形及质量分布,用于计算碎片云对后续薄板的侵彻效果。
2006年Schafer[133]将碎片云分为中心大碎块、弹丸碎片和薄板碎片3部分,如图25所示。外形上以椭球壳代表薄板碎片云,以球壳代表弹丸碎片云,二者头部相切,中心大碎块位于切点处,与碎片云实验图像很接近。质量分布基于面密度,假设薄板碎片云均匀分布于椭球壳,弹丸碎片则参考经验公式取指数分布,越靠前质量越大。运动速度由于椭球壳假设,计算更为复杂,多假设椭球壳和球壳相切处曲率相等,以及椭球壳尾端零速度。另外,此前均为连续模型,此模型为离散模型,碎片平均大小参照Grady破碎准则计算,撞击能量耗散参数和中心大碎片尺寸由经验公式获得,应变率相关参数通过对比数值计算与实验结果确定。该模型的设定与实验更加接近,特别是离散化处理和中心大碎片,为未来研究提供了新思路,但计算复杂。
国内郑建东等[134]在Schonberg模型基础上,参照Schafer模型弹丸碎片位置假设,提出图26所示模型,碎片云质量分布和运动速度同Schonberg模型。该模型形式简单,工程计算使用方便,但薄板碎片云外形与实验不太相符。
Zhang等[135]针对多层薄板情况,建立了球形弹丸碎片云模型,模型设定与Swift模型基本一致,额外考虑了薄板破裂耗能,利用临界动量面密度值判定薄板是否破裂及碎片能够通过。最新的模型当属由Wang等[136]在Zhang等[135]的模型基础上提出,针对长圆柱体打击多层薄板,将碎片云分为内外两层,外层为真正碎片云,内层为尚未破碎的剩余弹体段。第1层薄板后碎片云外形假定为椭球壳,质量取指数分布,运动速度假设尾端零速度,其他特征值来自经验公式。其假定若外层碎片足以穿透下一层薄板,则穿透后的新外层碎片外形为球壳,内层不变;否则忽略外层,由内层剩余弹体直接侵彻,设定参照第1层薄板后碎片云。这两个模型引入了薄板破裂耗能,很好地结合了工程问题,未来对碎片云侵彻性能的建模研究或将向此方向发展,将更完善精确的碎片云模型拓展到侵彻计算中。
总体来看,Swift类模型侧重工程计算,结合基本动力学守恒和一些假定条件提出。然而,这些假定也限定了模型的适用范围,如Swift模型只适用于碎片材料完全熔化或气化时;Schonberg模型将弹和薄板碎片云分离,适用于完整形态的固、液、气相碎片云[5];郑建东等加入了大中心碎块,使适用范围扩展到弹丸初始破碎阶段的非完整形态碎片云;Corvonato模型在原文中只测试了膨胀半角基本不变的速度段内情况;Schafer模型只针对完整形态碎片云,不包括完全熔化后情况。综上所述,Swift类模型大多针对特定阶段,根据对碎片云的直接观测提出,需加强基本规律分析,以减少假定条件限制,尝试建立多工况适用的统一模型。
回顾Swift类模型发展历程,外形上将弹和薄板碎片云分离,尝试非球形外形;质量分布描述引入非均态分布函数,模型越来越接近实验结果;但同时导致速度分布计算复杂,不得不引入相关假设或依赖经验结果。未来的模型应改进外形和速度分布假设并离散化处理,以及向侵彻极限评估方面拓展。另外,要结合各阶段模型寻找共性,尝试综合并简化,而不是表述愈加复杂,实用性却降低。
3.2 Piekutowski模型类
基于对实验图像的观察,Piekutowski[69]在1990年提出了如图27所示的圆盘弹丸碎片云模型。考虑到碎片云侵彻性能,模型忽略外泡结构核圆盘碎片云前端部分(分界线右侧虚线三角区域),以两个梯形实体描述薄板和圆盘碎片云,4个特征速度表达速度分布。不同于Swift类模型大多用弹孔大小计算薄板碎片质量,该模型假设与圆盘等径大小薄板被冲下并形成碎片云。由动量守恒计算交界面轴向速度va,径向膨胀速度vrad由实验图像直接测量,其余由一维应力波分析程序计算。计算速度时,其假设冲孔过程无动量损耗,模型内各点速度由到特征点的距离线性插值。Piekutowski模型主要用于简化碎片云结构,考虑碎片云侵彻性能。图27中d为盘形弹丸直径。
基于Piekutowski模型框架,Bless[137]改进了模型并完整地从理论上推导了特征速度,结果见图28(a)。考虑到薄板厚度小于弹体轴向尺寸,轴向两列相向稀疏波在弹体内相遇,模型将薄板碎片云置于最前端,弹体碎片云分前后两部分,基于3个轴向和1个径向特征速度描述碎片云运动。Bless理论分析了图28(b)和图28(c)所示冲击波与稀疏波的作用过程。图28(c)为弹板材料的应力σ与粒子速度u的关系图,其中P、B直线表示弹丸和薄板材料的线性Hugoniot关系(忽略了加载、卸载间的差别)。计算4个特征速度值:u1=2us、u2=v0、u3=2us-v0、u4=v0-us(见图28),us为冲击波引起的粒子速度。其中速度u4基于轴向稀疏波导致的弹体材料速度改变量得到,理论依据不足。Bless模型沿袭了Piekutowski模型的基本假设,但速度值完全由理论计算得到,与实验吻合很好。相比而言,Bless模型过度简化外形,但其理论分析过程出色,搭建了形成过程到特征速度的分析框架。
进一步,Bless[137]认为当圆盘和薄板阻抗不同时,薄板背面稀疏波在材料界面反射,弹和薄板在界面处分离;若圆盘和薄板同种材料,则二者就不分离,形成球形碎片云共同运动;若是球形弹丸,则由于弹丸非线性几何形状影响,即使同种材料弹和薄板碎片仍会分离,此分析或可解释碎片云结构部分的切片实验结果。
1993年Yew等[12]结合Grady破碎准则和Piekutowski模型,并参照Elliot[138]提出的靶边缘径向速度计算径向膨胀速度,得到圆盘弹丸撞击薄板后特征速度理论结果和碎片平均尺寸。该工作完成了冲击波理论和破碎理论的结合,由初始撞击相关参数即可计算碎片云速度分布和碎片平均尺寸,为碎片云分布理论研究提供思路,不过平均尺寸和实验相差较大,且未获得尺寸分布。
前文中Schonberg[117]提出碎片云相态的计算方法同时建立了碎片云运动模型(见图29)。模型利用碎片云头部速度vf、质心速度vi、径向膨胀速度vrad和弹丸碎片云尾端速度vr描述弹丸材料完全碎化时的碎片云运动情况。若部分弹体由于冲击波被卸载而未显著径向膨胀,则无尾端速度vr,而由未加载弹体速度vpr描述,各速度的求解参考Swift模型和Bless模型。该模型考虑了弹体未完全破碎情况,拓展了不同长径比弹体下的模型适用性,同时引入了动能守恒,但仅描述碎片云运动。文献[81,83]将该模型运动和相态分布用于球形弹丸碎片云,计算结果与实验相符。
总体来看,Piekutowski类模型更注重碎片云特征的描述。模型参照碎片云形成过程分析,理论依据较充分,但都主要描述碎片云运动,模型结构过度简化。从最开始的实验模型,到完整理论分析,再到碎片平均尺寸、相态分布的拓展,不断完善碎片云各特征分布的模型化描述。然而,目前工程计算主要以球形弹丸为基准,导致此类模型发展缓慢,需尝试将模型拓展到球形弹丸情况下。事实上,Piekutowski类模型的发展,从机理认识到分布特性建模,从定性分析到定量化推算,基本代表了碎片云理论研究工作进程。
龙仁荣等[139]比较了Piekutowski模型、Bless模型和Swift模型,认为相比Piekutowski模型,Bless模型是最合理、最理论化的模型,二者都能很好地描述圆柱形弹体碎片云运动,但对球形弹丸碎片云效果较差。Swift模型简单,适用于球形弹丸碎片云,但计算结果和数值模拟相差较大,认为是此类模型普遍以弹孔大小计算,高估了薄板碎片质量,换为Piekutowski模型的与弹丸等径大小靶材效果更好。不过,实际薄板碎片质量应介于此二者之间,需分析弹孔形成两个阶段的分段。
这些比较反映了两类模型的主要问题,Piekutowski类模型过度简化,实用性较差;Swift类模型在参数选择上缺乏指导。另一方面,Swift类模型基于对特定实验观察提出,撞击条件改变后模型适用性将大打折扣,需要尝试融合两类模型提出的方法。
此外,径向膨胀速度的计算非常棘手,Piekutowski类模型未能基于形成过程分析侧向稀疏波,难以直接获得径向速度;Swift类模型基于能量守恒,通过经验化参数控制能量耗散,可参考图18分析理论推算该参数。
3.3 其他模型
国内Huang等[140]提出了一种碎片云分布模型数值构建方法,旨在快速提供符合碎片云特征分布函数的碎片分布结果。2.3.3节提到Liang等[101]提出一种SPH算法用来模拟碎片云的碎片识别方法,该方法基于此识别算法,首先通过大量数值模拟统计碎片云质量分布、速度分布、空间散射角与撞击条件关系;然后将新给定撞击条件代入关系式,得到该条件下的碎片云分布函数,再以动量守恒为判定准则,使用Monte Carlo模拟方法得到符合分布函数的碎片分布结果。相比于传统的数值模拟计算,该方法耗时短,适用于各种撞击条件。只要前期获得恰当的关系式,后期使用时即可快速获得不同撞击条件下的碎片云分布模型。该方法思路非常新颖,碎片云问题有明显的统计特性,必须重视统计学工具的应用,特别是新兴的数据分析工具。
4 碎片云侵彻性能研究
碎片云研究的工程目标是评估碎片云侵彻后续防护结构结果。本节介绍碎片云侵彻性能相关影响因素,及碎片云动量和动能分布研究和成果较少的碎片云侵彻性能量化。
4.1 碎片云侵彻性能概述
以临界失效最小靶板厚度作为碎片云侵彻性能量化表述,工程设计中针对具体防护结构总会测定其临界失效曲线,实际反映碎片云的侵彻性能。工程中一般使用撞击极限方程描述防护结构临界失效情况,对于确定防护结构,首先实验获得其临界失效曲线,然后提出极限方程来拟合失效曲线。然而,提出极限方程并不容易,以Whipple防护结构为例,最初方程由Cour-Palais[141]于1969年的超高速撞击会议上提出,而后经过3次修改直到Christiansen方程(2001年)[142],又于2006年Reimerdes等[143]提出新修正。随着防护设计工作的发展,基于神经网络算法的预测方案[144]也被提出,但不能显式提供关系式。可见,由碎片云侵彻性能研究直接给出该方程工程的价值重大。
防护结构中缓冲屏即本文中的薄板,设计中会优化防护屏的厚度和选材。板厚过小,薄板背面稀疏波会在冲击波遍历弹丸前将其卸载,产生大碎片;板厚下限只能保证冲击波遍历弹丸,若要弹丸充分破碎或相变,则需足够高的撞击压力[3]。板厚过大会增加航天器载荷,同时产生更多薄板碎片,提高碎片云的侵彻性能。薄板选材方面,新材料被不断提出,如黄鑫等[145]实验发现,在铝合金前加金属陶瓷梯度层可增大冲击波幅值,有利于碎化弹丸,其自身抗拉强度低而充分破碎,对后续靶板威胁小;Klavzar等[146]在泡沫铝中加Ni金属涂层,有效提高了抗侵彻能力,但同时增大了结构面密度;Higashide等[147]测试发现CFRP在板厚与弹径比t/D>1时性能优于同面密度铝合金薄板,但t/D<1时不能充分破碎弹丸。此类研究主要测试既定材料性能,缺乏对材料设计方案的优化建议,难以细致调整搭配方案。
除几何和材料因素外,环境温度对碎片云的影响研究有工程需求。研究表明低温下薄板弹孔变小,碎片云形状不规则,防护结构性能提高,但只在撞击速度较低时效果较明显[148],另外环境温度会影响厚靶超高速撞击的弹坑尺寸[149]。
本文围绕空间碎片防护展开,此处简要补充介绍微流星体防护研究。李斌[150]和孙英超[151]使用冰、聚丙烯、金刚石和火山岩等模拟微流星体材料,但实验撞击速度远低于微流星体真实速度。基于数值模拟,李斌[150]发现撞击速度大于6 km/s时,冰球形弹丸碎片云侵彻性能强于同尺寸同速度铝弹丸碎片云,认为是冰融化和气化温度低但比热容大,相变吸热后薄板碎片云未液化,侵彻性能增强。在薄板选材中也要重视碎片云相变程度的考察,需考虑材料比热容等影响,不能只专注破碎效果。单立等[152]利用冰弹丸撞击蜂窝板,发现当弹丸动能相差不大时,弹丸尺寸和蜂窝板结构对冰弹丸撞击效果影响大。Walker等[153]利用CTH软件计算冰微粒撞击Ti靶板,发现撞击速度16 km/s时Ti出现气化,冰粒形状会影响此速度阈值。目前类似冰的脆性、低融点材料弹丸完整发射难度很大,实验速度受限;数值模拟能获得丰富信息,但可靠性未知。
4.2 碎片云侵彻性能评估
碎片云模型研究中校验模型时,可用模型计算碎片云侵彻结果,并与既有极限方程对比,也可用模型计算碎片云撞击靶板载荷时间历程。Piekutowski[69]计算了载荷时间历程(见图30(a)),图30(a)中第1个峰值是由于前端碎片速度最大,第2个峰值由于碎片材料密度升高,第3个峰值由于质量分布假设不合实际。观察实验结果(见图30(b))发现只有两个主要峰值,分别由最前端高速碎片和碎片云内核部分的高密集度碎片产生。
实验结果中3条曲线峰值从上到下递减,3条曲线测试点自上而下依次为偏离速度轴线76 mm、38 mm、0 mm位置,可见距离轴线越远,载荷强度越低,而且峰值时间发生偏移[69]。此外,实验结果最上面曲线的第2个峰值比第1个高,可能是因为外泡结构碎片来自薄板弹孔后期剥离阶段,碎片较大且为固相,侵彻性能较强。此外,庞宝君等[154]分析了碎片云撞击下后墙声发射信号,发现与弹径、前薄板厚度和撞击速度相关,或可用于碎片云侵彻性能评估。
碎片云侵彻极限直接量化方面,1995年Cohen[155]基于单个碎片平均侵彻性能,假设碎片无重叠地独立侵彻后靶板,引入碎片云空间散射角和单个碎块侵彻弹坑深度经验公式,发现同种材料弹和薄板所产生碎片云侵彻后靶板弹坑深度。不过,此方法过多依赖于经验公式,且仅适用于t/D<0.5、s/D<32(s为薄板与后靶板间距)。相变方面,该方法适用于碎片云开始产生到材料完全熔化,由撞击速度和相变阈值速度线性插值得到液相和固相材料比例,并假设完全熔化速度阈值下碎片云前端材料完全熔化,而尾端的原本完整弹体完全破碎,正则化后的计算结果与实验吻合较好。此研究意义在于提供了撞击参数到碎片云侵彻性能直接计算式,贯穿了碎片云研究出发点和目的,且影响因素考虑全面,但假设和简化过多,特别是完全平均化普通碎片。此外,该文专门考虑剩余弹体或大碎片侵彻性能贡献,最终靶板弹坑深度为大碎片和平均化的碎片云侵彻深度之和。
丁莉[156]分弹道段、破碎段和液化/气化段,基于对物理过程的认识和量纲分析,拟合现有实验数据,构建了完整的碎片云侵彻极限方程,与实验结果吻合较好。此工作完整搭建了体系框架,并考虑了各工况段适用范围。碎片云侵彻极限研究要细化各分段的极限曲线变化机理,定量分析侵彻极限的影响因素变化;其次要整合各分段,采用模糊的分段方案,提高分段处的预测准确性。
2011年 Ryan等[157]提出弹丸破碎段中心大碎片侵彻性能即碎片云侵彻极限,基于中心大碎片实验数据[20]和单层板极限板厚经验公式来量化碎片云侵彻极限。其假设弹丸充分破碎后中心大碎片尺寸不再变化,重现了弹丸破碎段侵彻性能先降后升的变化,而非传统撞击极限方程单调递减,并通过实验验证了该变化合理。不过,Ryan等未验证最大碎片侵彻性能与碎片云侵彻极限的实际差距,包括碎片重叠侵彻效应和最大碎片是否为侵彻性能最强碎片,同时适用工况段分界速度固定且取值缺乏考量。本文认为,此研究重在以单个碎片替代整个碎片云计算侵彻极限,分析碎片云侵彻性能的变化机理,只是细节需讨论改进。邸德宁[158]定量分析了弹丸破碎段内中心大碎片特征变化及其与整个碎片云侵彻的极限偏差,但只能验证中心大碎片在相变前是最危险碎片。因此,本文建议考察各工况段碎片云中的“最危险碎片”,包括其归属及其对碎片云侵彻极限的贡献,如中心大碎片在相变后一段工况内动能依然最大,但是否是最危险碎片。
数值模拟可方便地计算碎片云侵彻性能、动量和能量分布、载荷时间历程等,但应用最广的SPH算法本身却存在拉伸不稳定、时间复杂度高、精度不足、物理边界施加困难问题,限制了数值模拟在侵彻性能量化方面的应用。尤其时间复杂度问题,SPH算法在物理量核函数近似时需要搜索近临粒子,时间复杂度可达O(N2),严重约束了计算效率和计算模型粒子总数。
针对计算效率问题,1997年Groenenboom[159]尝试FEM-SPH耦合建模方法,减小了模型SPH粒子数;武玉玉等[160]利用FEM-SPH耦合建模方法求解碎片云问题;赵士操[161]利用分解计算技术将碎片云形成、后续靶板侵彻等独立过程分割计算,并在靶板变形后期将板内SPH粒子粗化为大尺度粒子,甚至将靶板转为FEM壳单元模型。这些尝试有一定改良效果但程度有限,仍需改进SPH无网格思想。另一方面,随着计算机的普及和性能的提升,研究者们尝试SPH算法并行化计算,已有JOSEPHINE[162]和基于动态区域分解的PTS[163]等软件。
其他一些数值算法亦被用于碎片云问题,Ma等[164]详细比较了SPH和物质点法(MPM)在算法稳定性、计算效率、便捷性等方面的差别;Lian等[165]提出了一种自适应有限元MPM (AFEMP);冯春等[166]提出了一种基于颗粒接触的二维无网格方法(PCMM);Li等[167]利用最佳输运无网格方法(OTM)求解了碎片云问题;Johnson等[168]将一种结合粒子和有限元的方法(CPEM)应用于高速碰撞问题;于超等[169]、Jaramillo-Botero等[170]将分子动力学模拟拓展到了碎片云问题。总体而言,大多数算法是针对有限元和粒子算法缺陷的改进,特别是AFEMP、CPEM等根据材料变形程度自动选择有限元或粒子类算法,在计算资源有限的当前或大有可为。
迟润强等[171]利用AUTODYN软件中的SPH模块计算了弹丸撞击薄板后穿透碎片云动量Md和反溅碎片云动量Me与弹丸原始动量Ms的比值,发现穿透碎片云动量比Md/Ms与撞击速度呈幂函数关系。当Md/Ms<1时,动量比Md/Ms随撞击速度的增大而快速增大,随板厚的增大而减小;当Md/Ms>1时,Md/Ms随撞击速度的增大缓慢增大,随板厚的增大而增大。反溅碎片云动量比Me/Ms随撞击速度和板厚的增大而增大。迟润强等还提出Md/Ms和Me/Ms拟合公式,建立碎片云模型时可参考该公式判断是否能直接忽略反溅碎片云部分的动量贡献,或直接将关系式引入模型。
碎片云动量和动能分布测试手段不足,LeMaster等[172]于1992年利用摆式动量测试探头测量碎片云动量分布,仅得到少量数据,提出“三角形”分布规律。最近有Song等[173]提出了一种利用接收靶与激光位移干涉仪的实验方案,可实现碎片云空间动量分布的定量测试,但尚无更进一步的信息。
王惠等[174]通过数值模拟发现,碎片云动量确实大致呈三角形分布,但并不是随着到轴线距离的增大而线性递减。由于该规律受统计方式的影响较大,暂无更确切的结论。同时,计算发现在3~7 km/s撞击速度范围内,随着速度的增大碎片云径向扩散变大,动量密度峰值降低,对后墙损伤减弱,但该结论与碎片云侵彻极限的波动变化不一致,可能是因为未考虑材料相变。关于统计方式,借助碎片识别技术,基于碎片而不是SPH粒子统计侵彻数据,或有较大改观。
碎片动能测量只有数值模拟结果,贾光辉等[175]通过数值模拟得到了碎片云比动能,进而得到粒子在单位圆环面积上的比动能之和函数形式为
(12)
在镁合金和铝合金薄板对比研究中发现,镁合金薄板的碎片云前端粒子速度大于铝合金,但由于密度差异,铝合金薄板前端粒子动能更大,被认为侵彻性能更强[176]。由此可见,碎片云侵彻性能研究需同时考虑碎片云速度分布、质量分布。
碎片云动量和动能测量实为碎片危险性测量,尝试表征碎片侵彻性能,但材料相态不可忽略,如材料相变后碎片云边缘处存在固体碎块,其侵彻性能可能强于前端高速液态碎片。类似地,最危险碎片的确定也需要两个步骤:寻找动能或动量最大碎片;评估该碎片相态及温度带来的影响。此外,随着撞击速度的增大弹靶材料可压缩性不同带来的侵彻结果差异增大,目前研究中弹靶多同为铝合金材料,可压缩性差异小,暂不必考虑其影响。
综上所述,碎片云模型可直接推导出其动量和能量分布,但建模中未充分关注碎片云侵彻性能的计算准确性;同时侵彻性能分析结论缺乏,难以为碎片云建模提供参考。此外,侵彻极限研究流程清晰,但多关注计算结果准确性,临界曲线变化规律机理认知不足。
5 总结及展望
5.1 总结
本文参照物理过程,依次分析正撞击碎片云形成过程、分布特性、模型研究及侵彻性能,并希望达成两方面成果:整合全局,强调具体研究方向之间的关联,推动整体框架的完善和填充;梳理各方向的主要进展,尤其是新兴工具及技术,促进后续分析和挖掘工作跟进。
碎片云形成过程研究要揭示其形成机理以指导后续研究,目前能定性解释机理,但缺少定量关系,需要建立球形弹丸从冲击波到稀疏波分布模型。现有研究已初步揭示弹丸冲击波特征变化,但稀疏波产生及变化情况未知。稀疏波作用下材料破裂已有基础工作,结合波系分布可推导碎片云分布特性。薄板方面关注弹孔,形成机理分析可与弹体类比,相互参考。
碎片云分布特性研究广泛,速度分布目前基于特征点描述,能初步解释碎片云外形和结构变化,但相关工作缺乏。质量分布理论分析受限于形成过程和材料动态破坏认知不足,实验测量技术不够直接和精准,数值模拟有碎片识别技术可尝试,但门槛较高。相态分布借助辐射测量技术取得较大进展,可依此校正数值工具,特别是状态方程选择,理论建模需要跟进,且并入碎片云整体模型中。
碎片云模型研究即分布特性模型化,主要有两条思路:参照碎片云宏观表现直接建模,如Swift类模型,考虑碎片云外形、质量分布和速度描述,要注意模型泛化能力和实用性,切误过度追求与实验接近程度;沿碎片云形成过程建模,如Bless模型,但受限于形成过程认知不足,模型简化严重,工程实用价值低,但为此研究布局提供了框架,从撞击参数到分布结果。另外,需解决径向膨胀速度计算,并尝试引入相态分布。
碎片云侵彻性能研究要与工程需求对接,直接建立碎片云侵彻极限公式代价较大。碎片云建模中未充分考虑侵彻性能计算结果准确性,有其计算的动量、动能分布可靠性不佳。借助中心大碎片量化弹丸破碎段侵彻极限思路较好,应当进一步分析碎片特征变化规律,借此解释临界曲线变化机理。
研究工具改进不容忽视,如碎片温度测量技术和SPH方法计算效率问题,技术突破后要跟进数据分析和机理挖掘。理论方面现已有大量基础实验数据和经验公式可借鉴,应当尝试填充研究框架,尝试稀疏波作用到碎片云分布特性。在本文之外,斜撞击情况与工程实际联系紧密,现有分析工作深度不足,要尝试分析形成过程并与正撞击工况统一模型。
5.2 发展趋势
随着数值模拟过程中碎片识别和特征提取技术的完善,将实现单个碎片特征和碎片云中碎片特征分布的测量。本文认为,未来的碎片云研究主要转变来自认知角度:以往的研究方法是直接观测碎片云宏观特性,但碎片云本就是大量独立碎片的集合,未来将由单个碎片特征统计入手构建碎片云。
研究内容方面,数值模拟过程中碎片识别和三相状态方程的发展,实验中碎片云电磁辐射温度测量技术的突破,将重点考察碎片云的质量和相态分布。质量分布包括碎片尺寸及形状空间分布和碎片尺寸数量分布,并关注较大碎片特征随撞击工况的变化。碎片云相态分布关注材料相态总体分布规律和单个碎片温度变化和相态,同时以实验数据为基准考察数值模拟材料模型的选择。碎片识别的实现,意味着数值模拟中碎片云特性测量将基于碎片,而不是以往的SPH粒子。由测量整个碎片云获得的碎片云速度分布,将从大量碎片速度入手重新描述,特征位置或将被确定在具体碎片上。离散化碎片云模型将基于单个碎片特征与撞击工况关系及碎片云中碎片的特征分布建立,追求整体分布特性和侵彻性能与实验一致。
随着碎片识别数据的分析挖掘,将分析特征变化机理并关注碎片云的形成过程。除了直接由大量数据拟合经验公式,将尝试从形成过程入手建立撞击工况到碎片云特征分布和碎片特征关系,如借助层裂理论推导单个碎片速度。进一步,碎片云整体侵彻性能将被分解到具体碎片尺度,观测贡献较大碎片的侵彻性能变化,分析碎片云侵彻极限变化的机理,这也将完善整个碎片云的研究框架,指导防护结构设计选材。
5.3 研究建议
当前可行的一些研究建议如下:
1)分析碎片云的形成过程。需要着重认识弹丸内冲击波传播与衰减及稀疏波作用对碎片形成的作用机制过程;分析弹丸的不同形状、材料及撞击初始条件对碎片云结构,如外形及构成和碎片云速度、质量及相态分布的影响;进一步合理构建正/斜撞击、弹体有俯仰角时的碎片云理论模型。
2)针对碎片云分布特性,需要着重开展碎片识别和特征提取技术研究。需要特别关注SPH算法数值模拟后处理中的碎片识别,其中,基于粒子距离识别碎片的方案可靠性欠缺,可引入粒子速度、原始位置等,分层次比较筛选同碎片的粒子。针对具体碎片,需要建立相应的实验技术以多角度或分块观测重构碎片三维结构。碎片温度测量技术需要提高数据可靠性,对应地,要探索合适的数值模拟状态方程。
3)完善碎片云模型研究框架。需要重视建立撞击工况与碎片云整体分布结果的变化关系,传统的人工假设碎片云速度和质量分布限制了模型适用范围,尝试直接由撞击参数推算分布特性,并进一步校验侵彻性能计算结果的可靠性。离散的碎片云模型需要实现特征分布描述而非完全平均化,同时材料相态分布要直接引入模型。
4)量化碎片云侵彻性能。直接拟合实验数据获得的撞击极限方程细节准确性不佳,需要分析碎片云侵彻性能曲线波动变化的实质,修正弹丸破碎段和液化/气化段极限方程形式。其中,以单个“最危险碎片”近似计算碎片云侵彻极限便于分析,需要注重分析材料相变后最危险碎片的归属和侵彻极限量化,包括针对不同相态碎片的侵彻性能强弱标准。
5)优化薄板材料设计。很多新材料被用于空间防护,如金属基陶瓷、铝镁合金、金属玻璃、纤维编织材料、多功能密度梯度材料等。新材料带来的防护效果提升缺乏深入的机理分析,需要在传统铝板研究基础上,分析其对应的碎片云形成过程和分布特性差异,特别是弹丸破碎和相变程度变化,进而分析其碎片云的侵彻性能。相关研究应重点突出与传统铝板撞击的不同,及由此开展薄板优化设计。
6)更高速度撞击下,弹/靶材料的相变愈加重要,但受实验发射技术和观测技术所限,相关研究比较滞后。新材料引入导致此问题更加突出。需要进一步研究相变如何影响碎片云形成、分布及对应的侵彻性能。另外,目前尚缺乏合适的多相态材料本构和状态方程,这是相关研究的基础。

