深基坑支护方案优选中层次分析法的应用研究

杨廒葆， 陈瑞敏

(河南理工大学 土木工程学院， 河南 焦作 454000)

随着城市的发展，建筑基坑开挖的深度也越来越大，深基坑工程成为了城市发展的趋势。而深基坑工程是一个比较复杂的系统工程，其支护是重中之重。深基坑支护方案的选择受到许多因素的影响，目前，所采用的支护类型较多，应选择合理的支护方案，采用先进的施工工艺，并将安全、可行、环保和施工便捷之间的关系进行正确处理是十分重要的[1-2]。

对深基坑支护方案的评判采用较多的方法有专家问卷调查法、加权平均法等[3]。刘保县等[4]将层次结构模型进行改进并利用变权层次分析法对深基坑支护方案进行优选。撒利伟等[5]利用层次分析法与灰色系统理论相结合的方法对深基坑支护方案进行优选。金志仁等[6]通过马氏距离判别分析理论，建立了距离判别法模型，并利用大量国内的深基坑支护方案对模型进行检验，证明了该方法的实用性。曹文贵等[7]引进相对优势度分析方法，建立了确定基坑支护方案的区间关联模糊优化方法，并通过工程实例计算，证明了该方法的可行性与合理性。郭自立等[8]在综合考虑影响深基坑支护结构选型各指标因素的基础上，建立了基于改进的模糊积分深基坑支护方案优选模型，并通过工程实例，验证了该方法的可行性与合理性。李立云等[9]利用关联分析建立了基于灰色关联模型的改进型层次分析法，不仅克服了层次分析法固有的局限性，还增强了层次分析法的适用性。蒋英礼等[10]提出改进的集对分析法用于深基坑支护方案优选研究，结合工程实例，证明了该方法的合理性和实用性。这些方法虽然都可以为深基坑支护方案的优选提供合理的途径，但也存在不足之处。

本文采用模糊层次分析法对深基坑支护方案作出评判，其优点是能将复杂的问题层次化，综合考虑了各种确定的和不确定的因素，通过计算得到一个定量的综合评判结果，可以真实反应基坑支护方案的优劣程度，从而选择出最优的深基坑支护方案。

1 基于层次分析法的深基坑支护方案

1.1 层次分析法的基本原理与步骤

20世纪70年代美国运筹学家、匹茨堡大学教授Saaty提出了一种层次权重决策分析方法，即层次分析法(Analytic Hierarchy Process，简称AHP)。AHP可以用来解决具有复杂层次结构的多指标决策问题，它可以通过建立递阶层次模型，把一个复杂问题进行逐层划分，从而达到解决问题的目的[11]。

其基本原理是[12]：①首先将影响基坑支护方案选择的各种因素按照因素间的相互隶属度关系组成一个递阶的、有序的，即根据实际问题的性质和要达到的目的将复杂问题层次化，将问题分解为不同的组成因素；②然后按照1～9标度尺构造出判断矩阵，从而确定出各因素相互之间的重要性程度，采用最大特征根法求解判断矩阵各因素的权重值，并进行层次单排序、层次总排序及一致性检验；③最后通过模糊综合评判的方法计算最低层相对于最高层(目标层)的综合评价值，并将结果作为评价和选择方案的依据。

用AHP对深基坑支护方案进行评判基本步骤包括[13]：①建立评估递阶层次模型；②构造判断矩阵；③层次单排序及一致性检验；④层次总排序及一致性检验。

1.2 建立评估递阶层次模型

深基坑支护是一个相当复杂的系统工程，除需要进行支护方案设计之外，还应包括止水降水措施、施工组织、工程监测及应急方案等内容；影响深基坑支护方案选择的因素众多，主要有工程的建筑特点、工程地质条件、水文地质条件、建筑场地的周边环境、施工技术及设备等等。深基坑支护方案的设计必需满足安全性、经济性和可行性；同样，在现今的管理理念中环境保护及文明施工也是十分重要的。因此，本文从安全可行、施工便捷、经济合理、环境影响、场地工程地质条件5个方面，选择了17个指标来对深基坑支护方案的优劣进行评价，建立了图1所示的评估递阶层次模型。

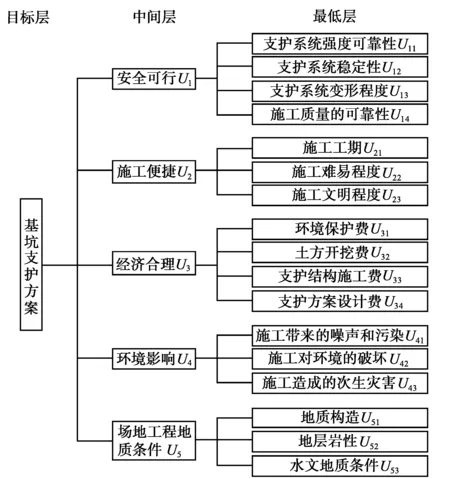
图1 深基坑支护评估递阶层次模型

1.3 构造判断矩阵

根据图1所建立的深基坑支护评估递阶层次模型，不同层元素之间的隶属度关系就被确定，而同一层元素之间重要性程度的比较可以采用1～9标度方法进行表示，形成判断矩阵A=(aij)m×n，标度如表1所示。

表1 1～9标度尺

1.4 层次单排序及一致性检验

1.4.1 层次单排序

层次单排序是从判断矩阵去推算本层次所有元素对上一层某元素而言的重要性排序，也即优劣排序。较严谨的排序方法是最大特征根法[14-15]，即求出最大特征根及特征向量，以特征向量作为元素重要性的代表。由于其准确度要求不高，故可用方根法近似求解，步骤如下：

(1) 计算判断矩阵A每一行元素的乘积mi：

, (i=1,2,…,m)；

(1)

(2) 计算mi的n次方根Mi：

(2)

(3) 将Mi作归一化处理：

(3)

则W=(W1，W2，…，Wm)T为所求的特征向量，归一化后的各分量为各元素的权重值；

(4) 计算判断矩阵A的最大特征根λmax：

(4)

式中Bi为向量B的第i个元素，B由下式求得

B=AW。

(5)

1.4.2 一致性检验

为了使构造的判断矩阵在逻辑上合理，还需要按式(6)对其进行一致性检验：

(6)

式中RI为平均随机一致性指标，由文献[16]可得其数值如表2所示；CI为一致性指标，由式(7)可得：

(7)

表2 平均随机一致性指标

则当CR<0.1时，认为层次单排序具有满意的一致性。各层指标因素判断矩阵及一致性检验如表3—表8所示。

表3 U-Ui判断矩阵及一致性检验

表4 U1-U1i判断矩阵及一致性检验

表5 U2-U2i判断矩阵及一致性检验

表 6 U3-U3i判断矩阵及一致性检验

表7 U4-U4i判断矩阵及一致性检验

表8 U5-U5i判断矩阵及一致性检验

1.5 层次总排序及一致性检验

在计算出各层元素的单排序权重后，采用式(8)所示的加权综合方法对评估模型进行层次总排序指标综合权重计算，将计算的结果利用式(9)进行一致性检验：

Wk=WijWi,i=1,2,…,n;j=1,2,…,n,

(8)

(9)

2 基坑支护方案模糊综合评判

2.1 单因素评判

根据文献[17-18]，本文建立评语集V=(v1，v2，v3，v4，v5)，分别对应状态良好、好、一般、差、很差5个等级，赋予对应的评估等级矩阵C=(5，4，3，2，1)，得到实践经验或逻辑推理从V到U的模糊映射见表9。

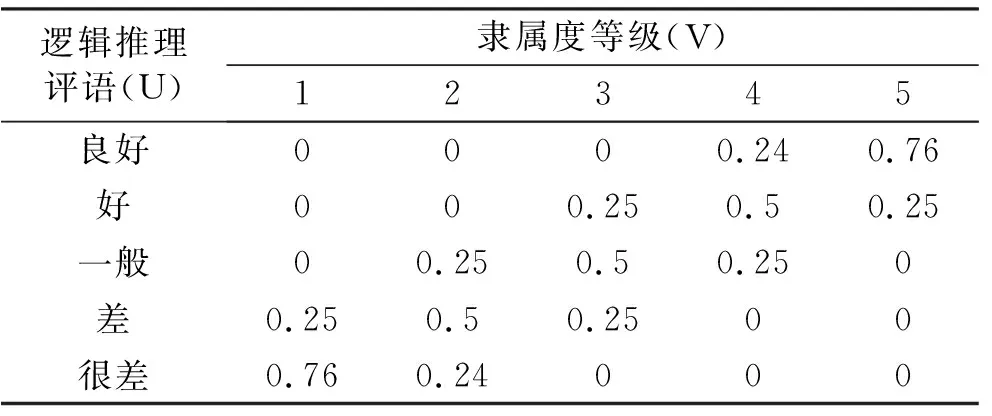
表9 V到U的模糊映射

2.2 建立模糊评判矩阵

将最低层各因素做单因素判断，最终形成深基坑支护方案的模糊矩阵[19]R=(rij)n×5，其中rij为第i个指标在评语集里对应第j个等级的比重，可以反映该指标所属的状态等级。

2.3 计算综合评判结果

由上述计算结果可得综合评估矩阵B，对矩阵B进行归一化处理，最终计算出深基坑支护方案的总综合评价值W′：

B=WR=[W1,W2,…,Wn]·R,

(10)

W′=B′CT。

(11)

3 工程实例

3.1 深基坑支护方案优选

以开封市黄泛区某深基坑工程为例，该基坑深9.5 m，所处地貌单元属冲洪积平原，根据工程现场实际情况，拟采用的支护方案有以下3种：①钻孔灌注桩+水泥搅拌桩+支撑；②喷锚网支护+单排深层搅拌桩防渗幕墙；③土钉墙+预应力锚杆+微型桩。3种支护方案各因素权重值及专家评价结果见表10，各因素权重值由表3—表8可得。

表10 各因素权重值及专家评价结果

3.2 模糊综合评判

针对方案一各因素进行综合评价，建立模糊评估判断矩阵R1，由2.1、3.1节可得

由2.3节可得

B1=WR1=[0.158,0.282,0.326,0.185,0.049]，

对B1进行归一化处理得

[0.158,0.280,0.323,0.190,0.049]，

最终计算得方案一的综合评估值为

4 结 论

采用层次分析法对深基坑支护方案进行评判，建立的深基坑递阶层次评判模型能够比较全面地反应影响基坑支护方案选择的因素，将构造的判断矩阵进行层次单排序、层次总排序计算并进行一致性检验，最后采用模糊综合评判法计算出基坑支护方案的综合评价值，并根据计算结果判断该支护方案的优劣。本文将该方法运用到工程实例中，通过计算选择出深基坑最优支护方案，与现场选择的支护方案相同，证明了该评判方法的科学性与可行性，为今后深基坑支护方案的选择提供理论依据。