深度学习背景下的小学数学模型建构
陈文渊
(松溪县实验小学,福建 松溪 353500)
数学模型是用数学语言概括地描述现实世界事物的特征、数量关系、和空间形式的一种数学结构。在义务教育阶段,用字母、数字及其他数学符号表达的数学的代数式、关系式、方程、函数、不等式及各种图表、图形等都是数学模型。[1]建构数学模型就是运用数学思想、数学的知识与技能去解决现实世界中实践问题的过程。在小学数学教学中,培养学生的建模思想,可以有效提升学生的数学素养,提高教学质量。教师在教学过程中应如何帮助学生建构模型,在学生深刻理解知识的同时,让学生的思维走向深刻。
一、精选问题,创设情境——建模的基础
数学模型都是具有生活背景的,这是建构模型的基础。教师应将生活中的素材及时引入课堂,将教材的内容通过生活中熟悉的事例,以情境的方式展示给学生,从而激发学生的学习兴趣,唤起学生对知识的渴望和追求。
比如在教学“路程、时间与速度”这一课时,有的教师是这样创设情境、导入新课的。
1.第一场比赛
师:昨天,我们班有三位同学为谁跑得快的问题争论不休,于是,他们举行了一场比赛,比赛结果如表1:
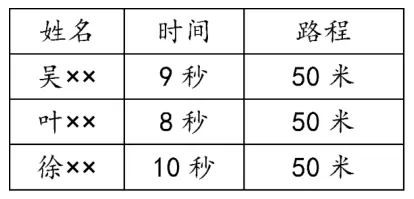
表1
师:从表1中你得到什么数学信息?有什么想法?
生1:我发现他们跑的时间不一样,但路程是一样的。
生2:我觉得叶××跑得最快,因为他用的时间最少。
师:也就是说,如果路程相同,比快慢只要比时间就行了。
2.第二场比赛
师:陈老师和叶××也参加了比赛,结果如下:
生3:还是叶××同学跑得快,两个人都跑了8秒,陈老师跑了48米,可叶××同学跑了50米。
师总结:如果用的时间相同,比谁快可以看路程(见表2)。
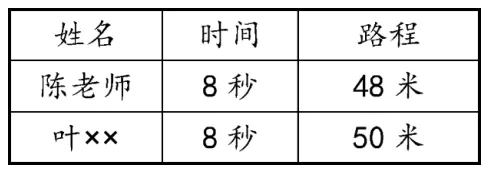
表2
3.第三场比赛
生4:陈老师和徐××跑的路程和用的时间都不相同,怎么知道谁快呢?(见表3)
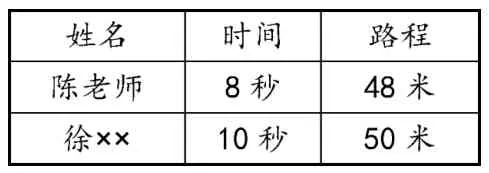
表3
生5:可以比速度。
陈老师:48÷8=6(米)徐××:50÷10=5(米)6米>5米
陈老师快。
师:这6米表示什么?5米呢?
生6:表示老师每秒跑6米,徐××每秒跑5米。
师:也可以说陈老师的速度是6米/秒,徐××的速度是5米/秒。[2]
本环节将跑步比赛这项活动引入课堂,能激发学生已有的生活经验,调动学生的学习兴趣。教师将不同的数据巧妙地蕴含在情境之中,使学生深刻体会,跑得快慢与时间和路程有关。如果时间和路程都不相同,要比速度,求速度的策略是应需而生,求速度的方法“路程÷时间=速度”这一模型也在教师的引导下一步步构建起来。
二、去伪存真,揭示本质——建模的关键
引导学生通过观察、比较、分析、抽象、概括等数学活动,剥掉外在的非本质因素,抽象出本质属性,得到模型,这是构建模型最关键的环节。
比如在教学苏教版四年级下册“乘法分配律”一课时,为了能在多变的问题情境中抓住不变的本质,笔者设计以下几个教学环节,构建“乘法分配律”的模型。
环节一:建立等式
师:(出示教师家客厅和厨房的平面图图1)一共要用多少块地砖?
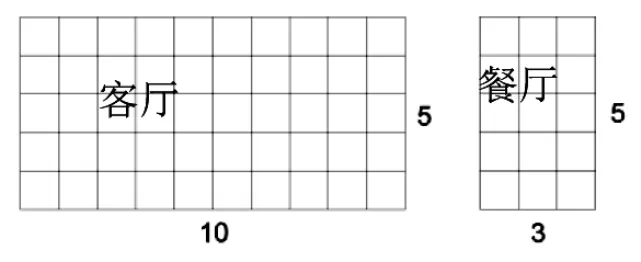
图1
生1:我是这样算的,10×5+3×5,分别算出客厅和餐厅需要的块数,再相加。
生2:(出示自己画的草图)你们看,两个房间合在一起,一行要13块,要铺5行,算式是(10+3)×5。
师:这两种方法有什么不同?结果相等吗?
生2:我算过了,结果都是65块。第一种方法是分开算,第二种方法是合起来算。
生1:其实不用算也知道相等,客厅铺了10个5块,餐厅铺了3个5块,10个5加3个5正好是13个5,所以相等。
环节二:加深理解
师:出示书房和卧室的平面图(如图2),这两个房间的面积有多大?
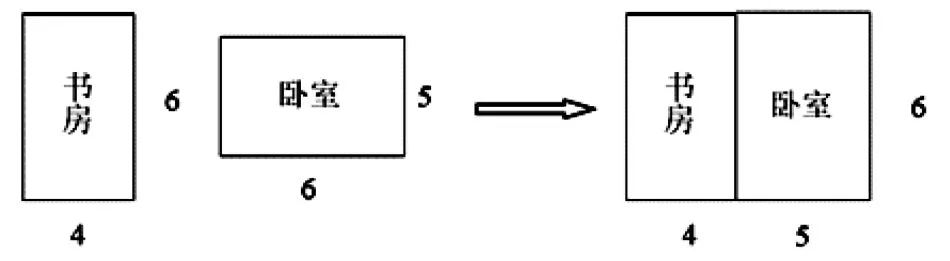
图2
生3:6×4+6×5或(4+5)×6
师:为什么可以合起来算?
生3:因为这两个长方形各有一条边是相同的,所以可以合成一个大的长方形,将不同的边相加,再乘以相同的边。
环节三:直观感受
师:该去买地砖和墙砖了,如果墙砖买20块,每块60元,地砖买40块,每块50元,我一共要用多少元?
生4:20×60+40×50先算出墙砖的价钱,再加上地砖的价钱就行了。
生5:我认为也可以合起来算,(20+40)×(60+50)。
生6:每块的价钱不一样,两种砖的块数也不一样,不可以合起来算。
师:出现了不同的意见,为了让大家一眼看出到底可不可以合起来算,我们可以用一个长方形的长表示墙砖每块的价钱,宽表示买的块数,那么,面积表示什么?(如图3)
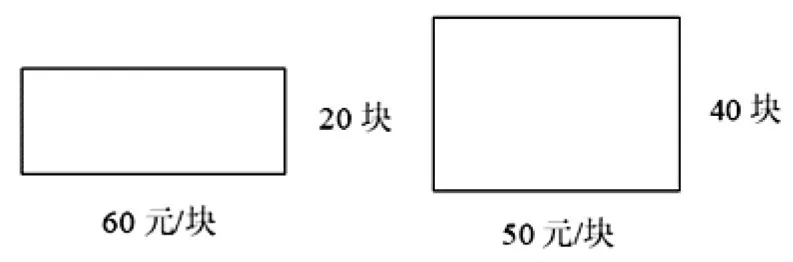
图3
生:表示墙砖的总价和地砖的总价。
师:现在能看出来为什么不能合在一起算了吗?
生:因为两个长方形没有一条边相同,所以不能合成一个大的长方形。
环节四:揭示本质
师:如果想要合起来算,该怎么办?
生:将题目中的条件改一改,如果买的块数一样,就可以合起来算了。
生:也可以买价格一样的砖,这样也可以合起来算。[3]
乘法分配律和其他运算律相比,结构更复杂,意义更隐蔽,对学生来说很抽象。如果只让学生记住“乘法分配律”的形,计算时,学生很容易将它和其他运算律混淆。在本节课的教学中,教师通过一个相同的长方形这一直观图示的形象支撑,将总块数、总面积、总价钱三个看似毫不相干的问题脱去生活的外衣,建立起乘法分配律的直观模型,每题中表示信息的两个长方形有一条边是相同,求面积才可以分别相乘再相加,也可以先求不同边的和再乘相同的边,使学生真正理解乘法分配律的本质特点,思维水平发生质的飞跃。
三、经历过程,浸润思想——建模的灵魂
数学思想是数学发生、发展的根本,是探索研究数学所依赖的基础,也是课程教学的精髓。因此,在建模的过程中,教师要适时渗透数学思想,增加建模思维的厚度,为学生的终身发展奠定坚实的基础。
比如在教学“口算两位数加两位数”一课时,笔者是这样引导学生解决问题的。
师:老师准备带二年级四个班的同学(各班人数如下表)去参观博物馆,每两个班同乘一辆车,请同学们当小小设计师,以小组为单位,帮忙设计乘车方案。

?
生1:(1)班和(2)班同乘一辆车,(3)班和(4)班同乘一辆车。
生2:(2)班和(3)班同乘一辆车,(1)班和(4)班同乘一辆车。
生3:(4)班和(3)班同乘一辆车,(1)班和(2)班同乘一辆车。
生4:第三种方案和第一种是一样的。
生5:方案没有写全。
师:同学们这样说,有点乱。能不能运用以前学习的排列组合的知识,来设计方案。
小组讨论后汇报:
第一种方案:(1)班和(2)、(3)班和(4)班同乘一辆车。
第二种方案:(1)班和(3)、(2)班和(4)班同乘一辆车。
第三种方案:(1)班和(4)、(2)班和(3)班同乘一辆车。
师:现在找全了吗?
生6:找全了。
师:为什么这次同学写的方案能让我们一眼就看出没有遗漏和重复的呢?
生7:因为我们是按照顺序进行排列、组合的,这样就不容易出现遗漏或重复的现象。
在以上的教学中,第一次写出来的方案是无序的,结果出现了重复或遗漏的现象,让学生感受到无序的杂乱。然后引导学生运用排列、组合的方法进行有序思考,从无序到有序。学生不仅解决了问题,还感受到有序思想的重要性,从而让思维走向深入。
四、举一反三,灵活运用——建模的延伸
用所建立的数学模型来解答生活中的数学问题,让学生体会到数学模型的实际应用价值,体验到所学知识的用途和益处,培养学生举一反三、灵活解决问题的能力,让思维走向深刻。
案例:《植树问题》教学片段
(课件出示)

师:如果有10个蘑菇,那么有多少朵花?
生1:有11朵花。可以把花想成树,把蘑菇想成间隔,就是两端都载树,棵树比间隔数多1。蘑菇的朵数+1=花的朵数。
生2:也可以把蘑菇想成树,那花就是间隔,这时,就是两端都不栽树,棵数比间隔数少1。蘑菇的朵数+1=花的朵数。
师:同学们观察的角度不一样,想的情况就不同,但是殊途同归,结果都是11朵。[4]其实生活中的很多问题都可以用植树问题来解决。比如将一根木头锯成5段,需要锯几次?
生3:需要锯四次,可以把每段长度看作间隔数,锯的次数看成树,相当于两端都不种,棵树等于间隔数减1。锯的次数=锯的段数-1。
生4:老师,我觉得昨天爬楼梯这个问题也可以用植树问题来解释,从1楼到3楼要30秒,那么,从1楼到10楼就要135秒。
生5:可以把楼层看作树,楼梯数看作间隔,1到3楼有3个楼层、2层楼梯,要30秒,爬一层楼梯要15秒,1到10楼有9个楼层,要15×9=135秒。
生6:我觉得敲钟问题也可以用这个方法来解决,如果把敲钟次数看作树,中间间隔的时间就可以看作间隔数。敲钟的次数=间隔的次数+1。
师:同学们可真能干,看来植树问题在生活中随处可见,其实解决这类问题的关键就是要明确把什么看作树,把什么看作间隔,再根据树与间隔之间的关系来解决问题。
数学模型来源于生活,也运用于生活,以植树问题为模型来解决生活中的问题,让模型更加丰满且具有生命力,同时培养了学生分析问题、解决问题的能力,深化模型的内涵,拓展模型的外延。在教师的精心引导下,学生的思维豁然开朗,举一反三的能力得到培养,数学模型的使用价值得以彰显。
总之,在小学数学课堂中,教师要将模型思想渗透于教学的过程中。要借助合适的素材,帮助学生建立有关的数学模型,不断总结建模的方法,让学生逐渐形成运用模型来解决问题的习惯和技能,为终身学习和可持续发展奠定基础。

