砂土地区浅埋非对称近接平行隧道施工地层位移分析

赵 文，陈 阳，李慎刚，唐志扬，柏 谦，张超哲

(1.东北大学 资源与土木工程学院， 辽宁 沈阳 110819； 2.广州地铁设计研究院有限公司， 广东 广州 510010)

随着人类对城市地下空间的开发，城市地铁越来越普遍。目前城市地铁大多采用平行双洞或多洞室进行排布，越来越多的浅埋非对称近接平行隧道被用于地铁施工中。双孔近接平行隧道间距较小，施工过程中相互影响较大，使得其开挖对地表及周围岩土体的影响程度和范围比单孔隧道更为显著[1-2]。隧道开挖地表沉降最典型的计算公式为Peck[3]公式，该公式已经从现场实测和模型实验两方面得到了验证，并基于此公式提出了不同的地表沉降的预测公式。随着隧道形式及地层情况的变化，Peck公式多次被修正以适应不同的地层及施工情况。Segaseta[4]给出了盾构隧道开挖层状地层引起的地表沉降半弹性解析解。为计算双线盾构隧道施工引起的地层内部土体沉降，魏纲[5]建立了修正的二维Peck公式，并探讨了il和ηl的取值方法。陈春来等[6]利用现有单线盾构施工引起的三维土体沉降计算方法，对魏纲二维深层土体沉降公式进行修正，从而拓展得到了双线平行隧道盾构施工引起的三维深层土体沉降计算公式。刘建航等[7]得出隧道沿纵轴线的纵向地表沉降预测公式提出负地层损失概念。刘波等[8]应用叠加原理，得出同一埋深双孔平行隧道修正Peck公式。张志强等[9]进行了非对称近接隧道施工力学特性研究，得出了先开挖较小断面隧道优于先开挖较大断面隧道的结论。李鹏飞等[10]基于塌落拱假定，考虑双线隧洞的不对称性，根据普氏理论推导了深埋情况的围岩压力计算公式。

本文针对砂土地区地铁横通道转两条非对称直径正线隧道项目，采用有限元软件模拟隧道不同开挖阶段工后地表沉降及隧道水平位移；基于Peck经验公式，应用叠加原理，得出相同收敛半径下非对称平行双线隧道地表沉降解析解，并与模拟值进行对比。

1 工程实例

1.1 工程基本情况

本文选取沈阳某地铁车站横通道正线和渡线断面的施工阶段进行研究，该区间左线长约1.23 km，右线长约1.26 km。场地范围内主要为砂岩和黏土互层，双线均采用矿山法施工，隧道顶覆土厚度6.00 m～18.00 m。

1.2 三维模型建立

1.2.1 隧道尺寸及土体参数

考虑到尺寸效应对研究对象的影响，一般选取模型水平方向3R～5R(R为隧道半径)，竖直方向隧洞底部向下至少取1R，隧道纵向长度取3R。本模型隧道半径R=6.4 m，13.2 m，模型长宽高分别为105 m，80 m，33.5 m。各土层地质参数见表1。

表1 土层参数[11]

注：T为土层厚度；MF为杂填土；SC为粉质黏土；C为黏土；MS为中砂；CS为粗砂；GS为砾砂。

土体本构采用摩尔-库仑(Mohr-Columb)破坏准则，隧道围岩，土体及初衬均采用有限差分软件FLAC3D中实体单元进行模拟，锁脚锚杆以及超前小导管采用梁单元模拟。模型材料参数见表2。

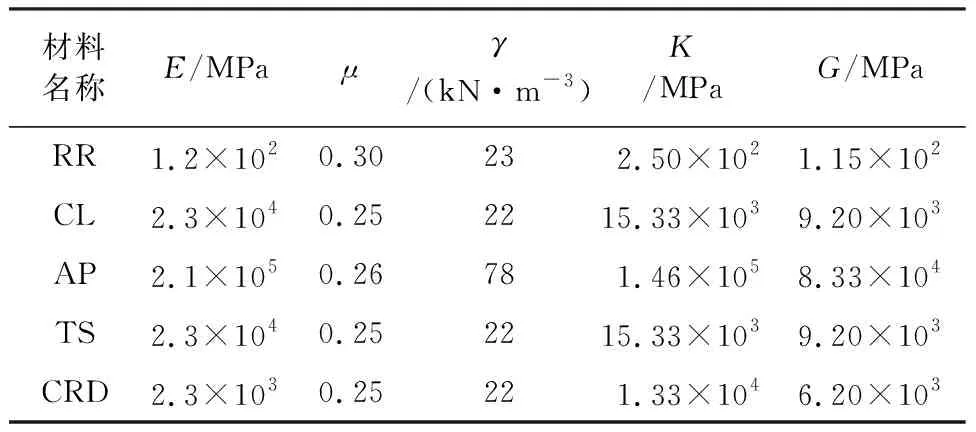
表2 模型材料参数

注：RR为加固圈；CL为格栅混凝土初衬；AP为锚杆及小导管；TS为临时支撑；CRD为中隔壁。

1.2.2 三维模型及施工步骤

由于FLAC3D前处理功能较弱，运用网格剖分软件Hypermesh将研究区三维CAD模型划分为31万个网格单元。双线隧道及横通道网格见图1。

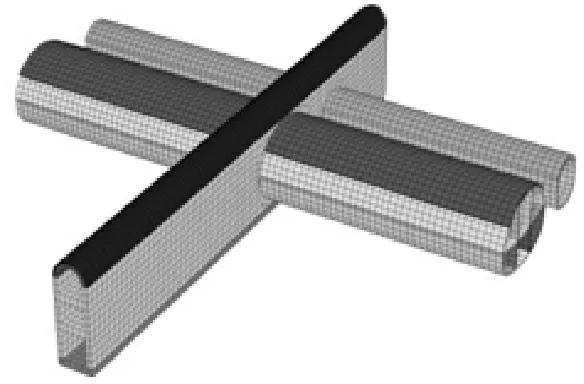
图1平行隧道模型网格图

三维土体侧面建立相对的水平约束，地面建立向上的法向约束，地表为自由边界，土体自重应力场进行初始地应力平衡，上部施工和设备荷载简化为均布可变荷载。隧道横截面示意图见图2。

图2隧道断面及地表沉降示意图

查阅文献[6]本文隧道开挖后断面半径均匀收缩半径a取0.005 m，各项参数见表3。

表3 平行双线隧道基本参数 单位：m

隧道正线及渡线段分别采用短台阶法开挖，和双侧壁导坑法开挖，开挖步序见表4(R为隧道洞径)。

表4 隧道断面开挖步骤

注：左侧标准断面和右侧大断面为Ⅰ，左侧大断面和右侧标准断面为Ⅱ。

1.3 计算结果分析

1.3.1 地表沉降分析

在模拟隧道开挖及施作衬砌的同时在模型上方设置地表沉降实时监测点，进行地表沉降监测和分析，图3为第Ⅰ阶段隧道开挖结束后地表沉降云图。

图3第Ⅰ阶段地表沉降图

由图3可知，第Ⅰ阶段开挖结束后的地表沉降位于小断面隧道洞顶，地表沉降量由洞顶隧道中线至两侧减小，最大沉降量为13.2 mm，小于控制值；地表沉降最大值出现于小断面跨度范围以内，整体沉降控制在大断面跨度之内，说明隧道整体支护效果良好，有效控制了围岩的变形。

第Ⅱ阶段开挖完成后的地表沉降云图如图4所示。由图4可知，第Ⅱ阶段开挖完成后的地表沉降最大值为15.6 mm，在控制范围以内，正线小断面和渡线大断面洞顶均出现沉降极值，沿隧道开挖断面位于双隧道中心距之间，沿隧道纵向方向最大沉降量集中在区间中间部位。右侧隧道先开挖大断面再开挖小断面，土体最大沉降量较小，最大地表沉降量位于小断面隧道顶部，由此看来，加强小断面隧道顶部监测非常必要。

各个施工阶段地表沉降极大值如表5所示，第Ⅰ阶段隧道开挖产生的地表沉降较第Ⅱ阶段大，第Ⅰ阶段和第Ⅱ阶段隧道开挖引起的沉降量分别占总沉降量的68.6%和15.4%，说明隧道开挖时，第Ⅰ阶段开挖对地表影响较大，该阶段开挖引起沉降量较第Ⅱ阶段大很多，但第Ⅱ阶段影响范围较大，约为第I阶段的2倍。

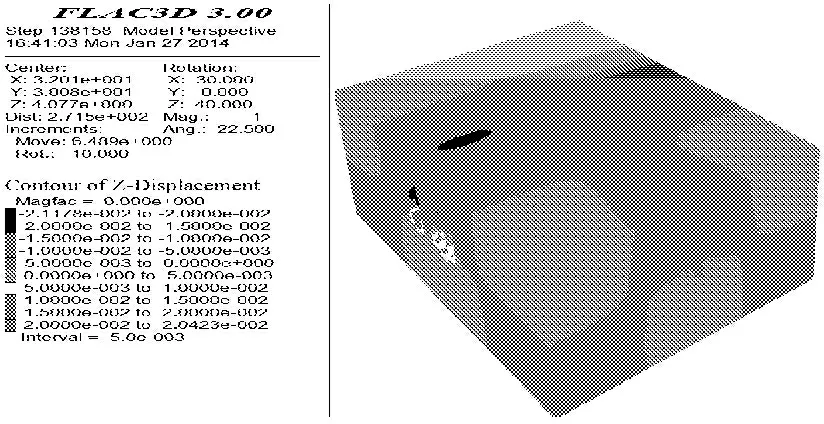
图4 第Ⅱ阶段地表沉降图

1.3.2 隧洞水平位移分析

图5、图6分别为横通道转正洞时隧道水平位移云图。由图可知隧道施工时横通道水平位移最大值约为11.98 mm，最大值位于双隧道之间，位于规范控制值之内。正线隧道开挖引起的左右两侧地表水平位移分别为5.90 mm和5.50 mm，位于标准断面隧道的右侧拱脚处，二者大小相当。正线隧道的水平位移小于横通道转正洞的水平位移，分析因为正线隧道拱脚的锁脚锚杆约束了正线隧道向洞内发生位移。

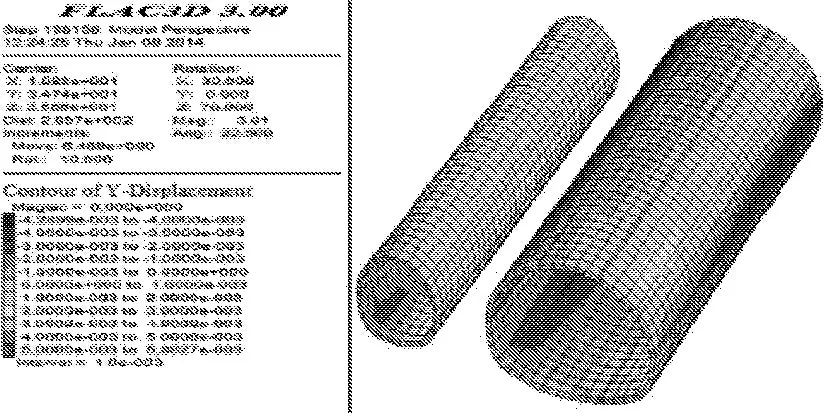
图5 横通道转正洞水平位移云图

图6正线隧道水平位移云图

2 横向地表沉降计算方法

众所周知，盾构隧道开挖引起的地层损失使地表发生沉降非常普遍。盾构开挖引起地层损失主要是由于盾尾间隙和衬砌自收缩的共同作用[12-13]，隧道开挖过程中开挖面土体变形主要由地层损失和收敛变形组成，本文仅考虑径向均匀收缩引起的地表沉降。以Peck公式表示地表沉降，其沉降表达式如下[14-16]：

S(x)=Smaxexp[-x2/(2i2)]

(1)

式中：Smax为隧道轴线对应地表沉降的极大值；x为测点与隧道重轴线的垂直距离；i为沉降槽宽度系数，其定义为地表沉降线反弯点与隧道中轴线的水平距离。

(2)

本工程实例中双线隧道为圆形断面，初始半径分别为R，r，隧道开挖引起断面收缩，均匀收缩半径为a，双线隧道埋深分别为H1，H2，双洞之间中心距为L(见图2)，由于双线隧道往往距离较近，由于开挖顺序不同，相互影响也不同，单隧道顶的地表沉降应为双隧道影响的相互叠加。基于Peck经验公式，根据叠加原理，得出非对称平行双线隧道地表沉降修正Peck公式为：

(3)

式中：Smax1为隧道T1中心的地表沉降的最大值；i1为隧道T1的沉降槽宽度系数；Smax2为隧道T2中心的地表沉降的最大值；i2为隧道T2的沉降槽宽度系数。

3 非对称双孔隧道沉降控制因素讨论

双孔隧道开挖引起地表沉降与隧道中心距、隧道直径及隧道开挖次序等因素有关[17-26]。下面以沈阳地铁九号线工程为例，运用修正Peck公式(3)，对砂土地区隧道开挖上方土体横向沉降的影响因素进行讨论。

3.1 双隧道中心距L改变

图7为非对称双线平行隧道先开挖大直径后开挖小直径隧道施工引起的横向地面沉降曲线，计算参数见表3，两条隧道的圆心距变化从1倍最小洞径到5倍最小洞径。图7为沿隧道纵向x=+B(B为大断面跨度)处的沉降曲线，不同平行隧道中心间距对应不同的地表沉降包络线。图7中y坐标左侧对应标准断面隧道，右侧为大直径隧道。相同条件下，随着圆心距L的增大，地面沉降曲线由正态分布曲线转换为马鞍形沉降曲线，地表最大沉降逐渐减小，地表沉降槽宽度系数随之增大；大直径隧道沉降槽宽度系数i1大于标准断面沉降槽宽度系数i2；由图7看出两条平行隧道距离越远，相互影响越小，产生的最大地表沉降量越小。

图7不同圆心距引起的地表沉降曲线

3.2 隧道埋深H改变

取沿隧道开挖方向x=-B处y轴右侧较大直径隧道为例，改变隧道覆土厚度，研究地层沉降随隧道埋深的变化。图8为不同埋深情况下的地表横向沉降曲线图，隧道埋深约从1倍洞径至5倍洞径。由图看出，随着埋深的增加，土体最大沉降量略有增大，最大沉降量从12.74 mm增大到13.13 mm，均处于控制沉降范围之内；沉降槽范围与埋深呈正相关，随着埋深的增大而增大。

图8不同埋深对应的地表沉降曲线

3.3 施工步序改变

图9为双线平行隧道开挖先后次序引起的地表横向沉降量图。分别取沿隧道开挖方向x=±B两个断面隧道断面，x=-B处先开挖小断面后开挖大断面，x=+B处相反。由图9可看出，隧道圆心距小于1倍洞径条件下，先开挖较小断面引起的地表沉降量最大值约7.80 mm，先开挖较大断面引起的地表沉降最大值约13.11 mm，先开挖较小断面隧道优于先开挖较大断面隧道。

图9不同施工次序地表沉降曲线

3.4 模拟沉降与施工步序关系分析

第Ⅰ开挖阶段先行隧道开挖结束后，后行隧道在先行隧道产生沉降的基础上继续对土体产生扰动，不同开挖次序产生的地表沉降量不同。取x=±B两个断面，分析各施工阶段后地表累计沉降规律，见图10。假设地层损失为径向均匀收缩5 mm。

图10x=-B各阶段工后地表沉降曲线(先小后大)

由图10、图11可知，第0步代表横通道开挖完成，准备正线隧道开挖。隧道开挖引起的最终沉降量为13.27 mm，位于大断面顶部正上方。x=-B断面代表先标准断面后大断面，第Ⅰ阶段和第Ⅱ阶段盾构开挖引起的地表最大沉降量分别为7.5 mm和5.8 mm，占总沉降量的56.5%和43.5%，发生在标准断面顶部，表明双线隧道施工第Ⅰ阶段开挖引起的沉降量占总沉降的比例较大。

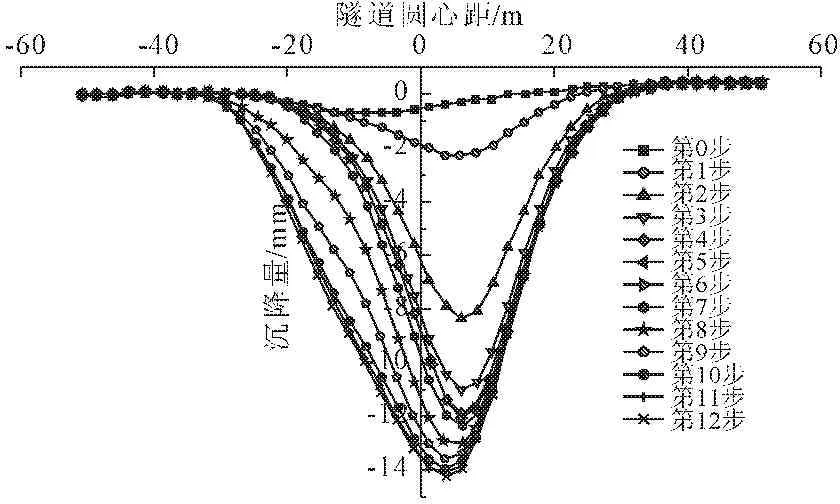
图11x=B各阶段工后地表沉降曲线(先大后小)

在x=B断面，开挖顺序为先开挖大断面再开挖小断面，工后最大沉降量为13.94 mm，其中第Ⅰ阶段和第Ⅱ阶段开挖引起的最大沉降量分别为12.13 mm和1.81 mm，约占总沉降量的85%和15%，最大地表沉降位于大断面隧道中线顶部位置。由此可见，隧道第Ⅱ阶段开挖引起地表产生的沉降量很小。综上可得，非对称双线隧道开挖时，先开挖大后小产生的地表沉降较小。

在断面x=B处，施工阶段第10～20步和断面x=-B处施工阶段第70～80步，对应大断面下导洞的开挖，工后地表沉降量为5.7 mm，约为总沉降的43%；断面x=B处，施工阶段20～30步和断面x=-B处，施工阶段80～90步工后地表沉降量为2.6 mm，约占地表总沉降量的20%。说明大断面下导洞及中洞上台阶的开挖均使围岩发生较大的变形，原因是因为隧道开挖使得洞周土体应力释放，因此，使用该方法进行隧道开挖施工时，应加强大断面下导洞和中洞的上台阶监测和支护措施。

4 结 论

(1) 为减小双隧道相互影响，平行隧道中心距应大于1倍洞径，平行双隧道第Ⅱ阶段的开挖对沉降的影响较第Ⅰ阶段小。

(2) 横通道转隧道正线的水平位移发生在横通道处；隧道间大直径断面拱脚处隧道正线水平位移显著，锁脚锚杆对水平位移的约束效果达54%。

(3) 论文给出砂层地区非对称平行隧道修正Peck公式，并讨论地表横向沉降影响因素。非对称隧道先开挖小断面再开挖大断面引起的地表沉降量较小。