层状地基中埋置管道动力阻抗函数的分析方法

张海廷，杨林青，郭 芳

(1.河南水利与环境职业学院， 河南 郑州 450008； 2.广东技术师范学院 天河学院， 广东 广州 510540； 3.河南农业职业学院， 河南 中牟 451450)

地下管道已经广泛地被用于能源、市政和水利工程等领域中，且国际上称地下管道工程为生命线工程[1]。目前求解地基中埋管的动力阻抗函数的主要方法为数值法和解析法相结合。数值法包括经典有限元法(FEM)、有限差分法(FDM)、边界法(BEM)等[2-3]；解析法通常采用波函数求解地基中埋管的动力阻抗函数。Pao等[4]利用数值法求解了半无限空间中洞室在入射波作用下的响应问题。Lee等[5]随后计算了半无限空间中有洞室存在的情况下SH波的散射问题。在弹性半空间的研究领域，蒋通等[6]利用解析法求解埋管的地基轴向刚度函数，然后蒋通等[7]对薄层法的原理与应用进行了详细的描述，并用薄层法对弹性层状地基中条形基础及各种基础的阻抗函数进行了分析[8]。由于薄层法具有一定的局限性，对于层状地基的动力分析计算，韩泽军等[9-11]针对复杂层状地基进行深入研究，利用精细积分算法提出了更加精确的算法，随后王朋等[12]利用此算法求解得到了层状地基内桩基础的动力阻抗函数。

目前对于地基的研究，多是将地基各向同性层状属性，而实际工程中的地基都有着不同程度的各向异性属性，本文就针对层状地基横观各向同性这一属性进行理论分析，利用方程变换和精细积分算法得到地基表面和内部任意点的位移响应，然后与容积算法相结合得到地基中埋置管道的动力阻抗函数。与文献结果对比的数值算例验证了本文算法的准确性，本文同时分析了层状地基的横观各向同性属性对地基中埋管动力阻抗函数的影响，将为今后的实际工程提供理论支持。

1 横观各向同性层状地基波动方程

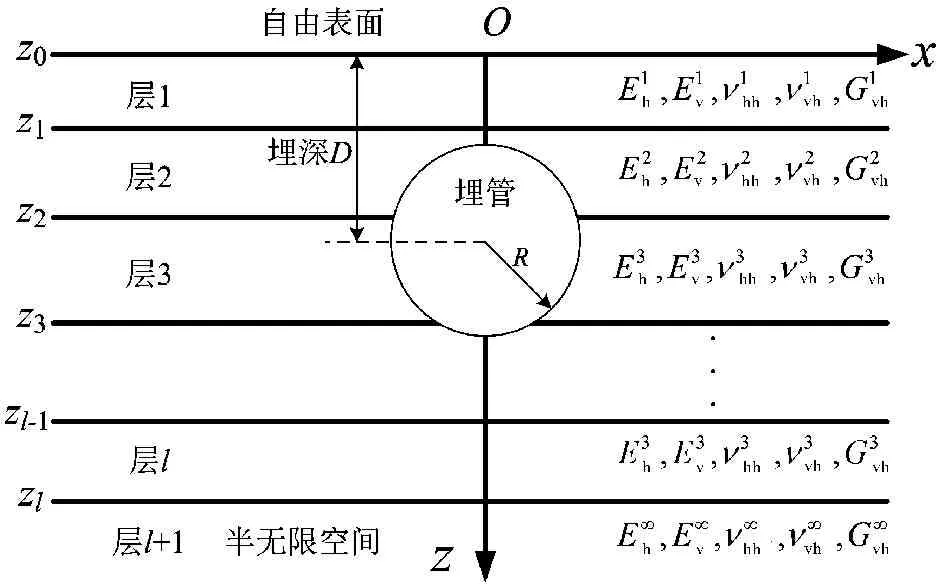
图1层状横观各向同性地基中埋置管道

层状横观各向同性地基广义平面波动问题波动方程中应力和位移只是x、z的函数，其频率-空间域内广义平面波动问题的动力控制方程为：

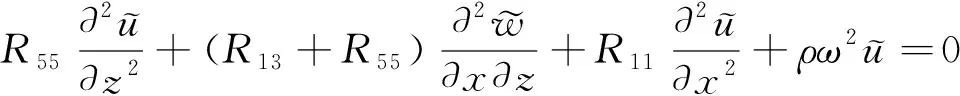
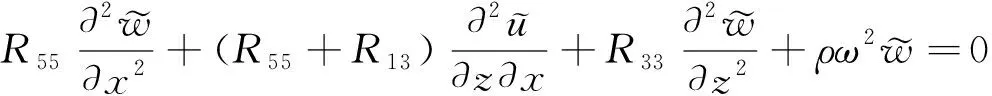
(1)

弹性矩阵系数与弹性参数的关系为：

R13=(Eh/v)vvh(1+vhh)

(2)

(3)

利用傅里叶积分变换，可定义频率-空间域和频率-波数域之间的关系转换式为：

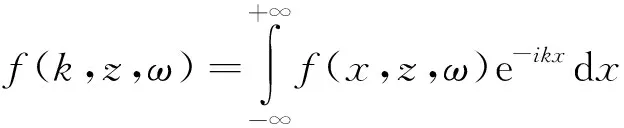
(4)

式中：ω表示的是角频率，k表示沿x方向上的波数；f(x,z,ω)和f(k,z,ω)表示位移或应力函数，前者是空间域内的，后者是波数域内的。

由方程(1)可以看出，波动方程解耦为x-z平面内的P-SV波(第(1)式和第(3)式)和x-z平面外的SH波(第(2)式)，本文只针对关于平面内的P-SV波的问题进行分析。因此，将方程(1)中的(1)式和(3)式合并后，利用公式(4)所示的傅里叶积分变换的第(1)式可以得到层状横观各向同性地基频率-波数域内的波动方程为：

K22q″+(K21-K12)q′-(K11-ρω2I)q=0

(5)

其中，I为2×2的单位矩阵；且

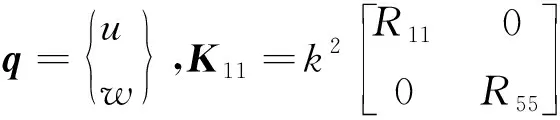
(6)

引入一个位移变量q的对偶应力向量p=-[τzxσz]T，其与广义平面波动问题中的层状横观各向同性地基问题的位移向量q满足以下关系：

p=-(K22q′+K21q)

(7)

利用位移向量q和引入的对偶应力向量p可以将层状横观各向同性地基频率-波数域内的波动方程(5)转换为以下形式的状态方程：

Φ′=HΦ

(8)

其中Φ=[qp]T，且

(9)

层状地基自由表面需要满足边界条件：

p0(z=0)=0

(10)

另外，层与层之间的交界处还应满足连续条件：

(11)

式中：+和-分别表示相邻两地基层交界处的上、下平面。

多层地基底部仍假定为半无限地基，l层底部的边界条件为：

pl=K∞ql

(12)

式中：K∞为半无限地基表面的动力刚度矩阵。

对于层状地基中的波动问题，本文采用精细积分算法进行求解，不仅可以有效地避免指数溢出的问题，并且具有较高的精度，具体求解过程可参见文献[14]。

2 层状地基内部任意点的位移响应

为了求解层状横观各向同性地基内部任意点的位移响应，必须要先得到层状地基内部体系的动力柔度矩阵。对于多层体系，假设在zk层面施加半宽为Δb幅值为pk的均布线荷载，求解任意层面(zk(k=0,1,2...n))上节点的位移响应，如图1所示。利用精细积分算法求解公式(8)，可以得出在任意线性保守体系内，层状地基上下面位移和应力向量的关系并将其转化成以下统一形式：

(13)

利用公式(12)和公式(13)组装得到所有层面的应力-位移方程：

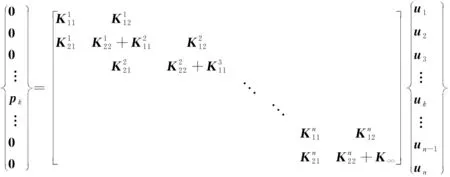
(14)

上式中K为频率-波数域内的刚度矩阵；P和U分别为层面处施加的荷载向量和位移向量。对矩阵K求逆可得任意点的位移解为：

U(κ,zi,ω)=FikP(κ,zk,ω) (i=0，1，2，…n)

(15)

式中F=K-1，动力柔度矩阵中的每一项Fik表示zi平面上单位均布荷载作用下上的位移响应。

公式(15)可以写成以下形式：

(16)

式中u(k,z,ω)和px(k,z,ω)为点在频率-波数域内的x向位移和荷载；w(k,z,ω)和pz(k,z,ω)为竖直z向位移和荷载。

对于公式(16)，利用傅里叶积分变换(公式(4))的第二式进行逆变换后可得地基内任意点位移和施加荷载点荷载的关系式为：

(17)

(18)

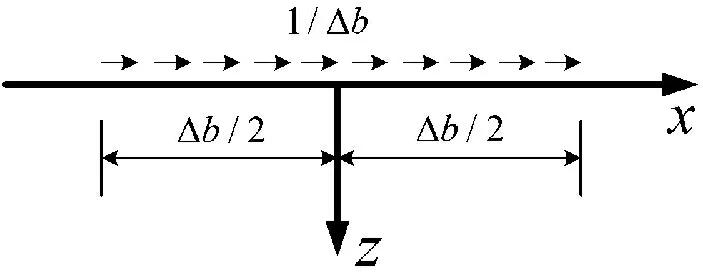
图2水平x向某个区间内作用有均布谐和力

对于水平x向均布荷载，利用公式(17)可得节点(x,z)处的位移响应为：

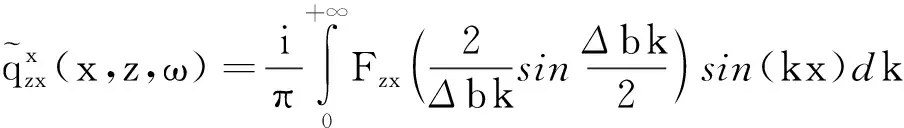
(19)

(20)

图3竖直z向某个区间内作用有均布谐和力

对于竖直z向均布荷载，利用公式(17)可得节点(x,z)处的位移响应为：

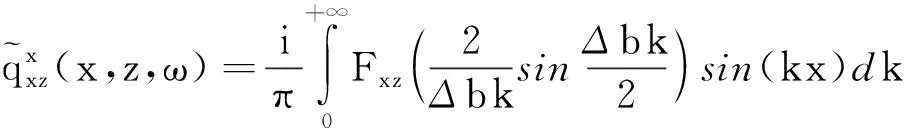
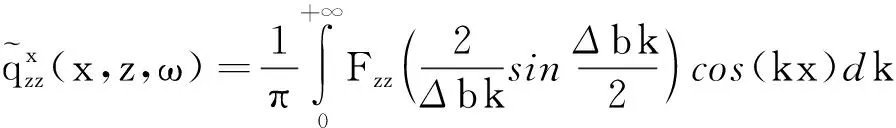
(21)

需要提出的是，公式(19)和公式(21)中的积分虽然为无穷Bessel函数积分，但低波数段部分对积分的结果起到了决定性作用，因此可以将无穷积分转化为有限积分进行处理，根据经验选取截断区间，对积分结果的影响很小。本文采用五点高斯积分进行求解，保证了数值计算的精度。

3 埋置管道的动力阻抗函数

本文针对埋管-层状地基体系，结合容积算法进行求解。埋置管道-地基体系动力阻抗函数的主要求解思路为(见图4)。

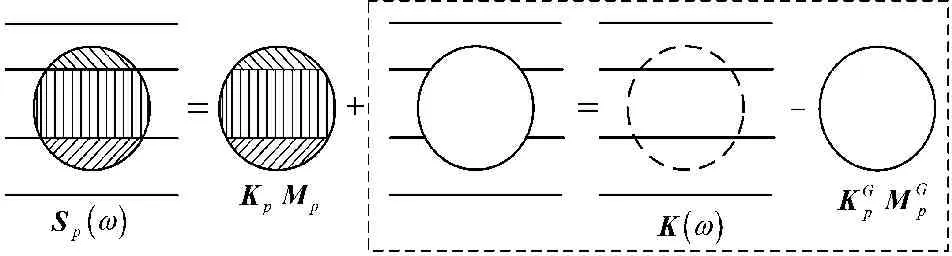
图4容积法的原理

(1) 先不在原层状横观各向同性地基内埋置管道，然后将准备要埋置管道的区域离散成节点群(含n个节点)，求解区域内离散节点群各自的位移响应，组成节点群的动力柔度矩阵：

(22)

(23)

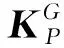
(24)

式中：K(ω)为节点群的动力刚度矩阵。

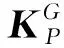
(25)

4 数值算例与参数分析

4.1 均质半无限地基中埋置刚性条带基础

因为广义平面波动问题中横观各向同性半无限地基中埋置管道的动力刚度矩阵计算方法类似于横观各向同性半无限地基中埋置有刚性条带基础的计算方法，所以这里引入一个刚性条带基础埋置于均质半无限地基中动力刚度矩阵的算例进行验证。宽度为2R的刚性条带基础埋置于均质半无限地基中，埋置深度为D=R/4(参考点到地基表面的距离，参考点取条带基础底部中心)。本算例中将分别选取两种均质材料来进行求解，两种材料各自的属性参数见表1，其中G为水平面的剪切模量，阻尼比ξs=ξp均取5%。为方便与已有的文献结果进行对比，条带基础的动力刚度矩阵系数按照下式转化为无量纲形式：

(26)

表1 横观各向同性半无限地基材料属性

4.2 横观各向同性的影响

半径为R的圆形管道埋置于层状横观各向同性半无限地基中，埋置深度为D=2R。为了研究层状地基的横观各向同性属性对地基中埋置管道动力阻抗函数的影响，本算例中选取两层地基且下卧弹性半无限地基的情况来进行分析。两个地基层及半无限地基层的材料属性见表2所示，对不同的地基层选取相同的比值n=Eh/Ev，并针对不同的水平向和竖直向弹性模量的比值n对埋管动力阻抗函数的影响进行分析研究(n=0.33，n=1.00，n=2.00)。将计算得到的埋管的动力刚度矩阵系数按照公式(26)转化为无量纲形式。计算结果显示n取不同的值时，地基中埋管动力刚度矩阵系数曲线的形状大致相同。当无量纲频率a0很小时，尽管比值n不同，水平、竖直刚度矩阵系数的实部和虚部变化均较小。随着a0的增大，水平刚度矩阵系数Khh的实部和虚部与比值n的大小成正比；竖直刚度矩阵系数Kvv的实部和虚部曲线就越早趋于平缓。而摇摆刚度矩阵系数Krr的实部和虚部与比值n的大小成反比。

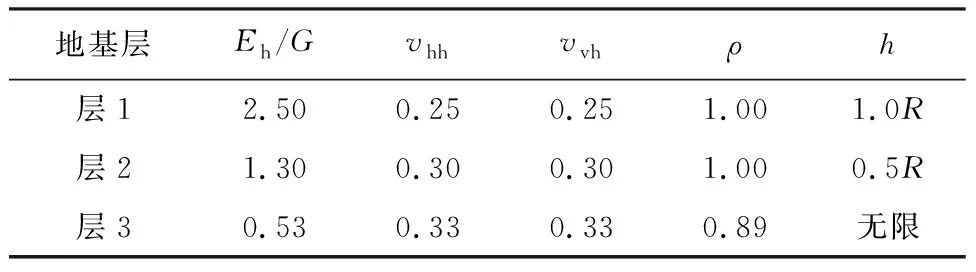
表2 两层层状地基和半无限地基材料属性

5 结 论

本文运用方程变换和精细积分算法，并结合容积法来求解层状地基中埋置管道的动力阻抗函数。此算法不仅对层状地基的厚度、层数及材料属性没有任何限制，而且过程中利用到精细积分算法，使得计算结果具有很高的精度。求解过程中涉及到的矩阵维数均较少，使计算更加简便，求解效率也得以保证，且矩阵数值求解稳定。利用算例得出的结果与文献的计算结果相比较，验证了本文算法的准确性。并结合算例针对层状地基的横观各向同性进行参数分析，结果表明地基的横观各向同性属性对层状地基中埋置管道的动力阻抗函数有着十分重要的影响。