腿-轮复合机器人全方位运动控制器的设计与仿真

辛亚先 ，李贻斌 ，荣学文 ，柴 汇 ，李 彬

（1.山东大学控制科学与工程学院，济南 250061；2.山东大学机器人研究中心，济南 250061；3.齐鲁工业大学（山东省科学院）数学与统计学院，济南 250353）

1 引 言

随着科技的发展，越来越多的自主侦察、运输、作战平台或智能机器人走向战场，代替士兵进入复杂地形环境实施作战或侦察任务。目前的移动式作战平台均采用履带式、轮式或腿足式移动方式行走。履带式和轮式移动平台的移动均需连续的支撑条件，适应地形变化的能力较差。而腿足式移动平台在平坦地面上的移动速度较慢，能耗较高。腿-轮复合移动机器人在结构化地形下运动速度快、效率高，同时能够工作在非结构环境下（崎岖不平的山地、丛林和冰雪地面等）。

目前，国内对腿-轮复合移动机器人的研究尚处在起始阶段，相对国外腿-轮复合移动机器人的研究存在较大差距。美国波士顿动力公司在军方资助下于2017年推出的仿人型腿-轮机器人Handle不仅能够在平坦地面快速移动，而且能够跳过垂直障碍、平稳通过左右陡直障碍、上下台阶等复杂地形环境，还具有较强的负重能力和受到外部干扰后的快速反应能力，证明了腿-轮机器人更好的实用性。另外，两轮机器人平台的研究开展较早，目前已有较为成熟的应用，如2002年Grasser F等人［1］研制了JOE两轮移动倒立摆平台，可实现自平衡与转弯；日本庆应大学搭建了两轮机械手平台，并提出诸多非线性控制方法［2-6］；2014年Kook A J等人［7］搭建了拥有两个机械手的两轮机器人平台，并对机器人与外界环境的交互力进行了分析与控制。迄今为止，将双足与两轮平台相结合的平台并不多见，2009年Lee H等人研制出BalBot Ⅴ［8］，将双足机器人固定于两轮移动平台上，通过遥控控制双足机器人踝关节转动，引起质心位置的前后变化，从而间接控制机器人行进速度。已有的两轮机器人平台大多不能调整平台高度，工作空间受到限制，身体或者机械臂均搭建在车架上，不可以改变身体姿态的冗余自由度，两轮之间、车架与身体之间相对位置固定，不利于通过崎岖不平地面，不利于身体的隔振。

两轮自平衡机器人平台作为典型的欠驱动非线性系统受到广泛关注，研究人员利用其对众多线性、非线性方法进行检验［9-15］，但在实际应用中，将机器人动力学模型在平衡点附近进行线性化，然后采用线性控制方法如LQR进行控制是最为常见的［16，17］，另外，利用不基于模型的PID控制方法对两轮自平衡机器人进行控制也获得了良好性能［18-21］。

本文对高动态、高效率的小型腿-轮复合移动平台的整体建模与控制进行了研究，采用模块化策略，对每一模块分别进行运动学与动力学分析，利用虚拟模型控制方法，将机器人整体虚拟为两轮一级倒立摆，各模块通过运动学解算与坐标变换得到倒立摆的虚拟质心，通过控制两轮输入力矩，实现平衡、行进与转向；通过控制腿部伸缩，实现平台的升高和降低；通过控制手臂关节，使末端执行器到达目标任务点；并进行了仿真实验以验证所提控制器的有效性。

2 机器人结构

机器人的结构示意图如图1所示，可将整体分为轮、腿、双臂、头部四部分，腿、双臂与头部通过驱动关节固连于躯干上。其中，两轮为轴线平行的驱动轮，通过施加适当驱动力实现平台的平衡、移动；每条腿配置两个俯仰关节，并通过一个欠驱动关节与驱动轮相连，可以通过控制腿部伸缩实现移动平台的升高和降低；本文暂不考虑手部末端执行器，每条手臂配置一个横滚关节，两个俯仰关节，可在手部目标位置进入手部工作空间后灵活执行任务；头部通过一个俯仰关节与躯干固连，本文未对其进行控制，未来将通过加入头部关节的控制实现对各种扰动与故障的反应式补偿。

由于机器人整体结构较复杂，控制难度大，本文采用解耦的分布式控制架构，腿与双臂根据平台高度要求与末端执行器目标位置的要求，作为两个子控制系统进行控制；虚拟倒立摆子系统通过控制轮的力矩，使得机器人在保持平衡的同时达到期望位置。针对以上三个控制模块，展开各模块的运动学与动力学建模，根据各模块控制任务的特点，构造适当的控制器。

图1 腿-轮复合式机器人结构示意图

本文仅考虑机器人姿态的矢状面运动，将双臂的横滚关节锁死，且左右手臂姿态相同，左右腿姿态相同，因此只在矢状面中展开运动学、动力学建模与控制。文中涉及到的机器人参数及其定义如表1所示。

3 系统建模

3.1 腿部运动学与动力学建模

腿部运动学与动力学分析在躯干坐标系中进行。两条腿结构相同，简化模型如图2所示。采用D-H方法，在每一连杆上固接一个坐标系，通过坐标系之间的平移、旋转关系描述连杆之间的相对位置。

表1 机器人参数及定义表

图2 以躯干坐标系为基坐标系的腿部简化模型

足端位置即腿部运动学方程为：

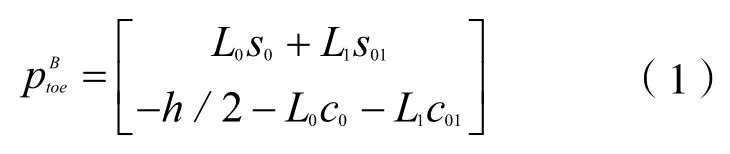
足端在y轴不存在运动，两腿的雅可比矩阵相同：

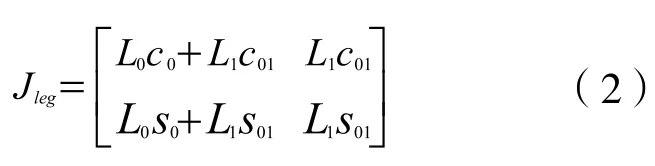
采用拉格朗日方法对腿部子系统进行动力学分析。腿部子系统的总动能可表示为：

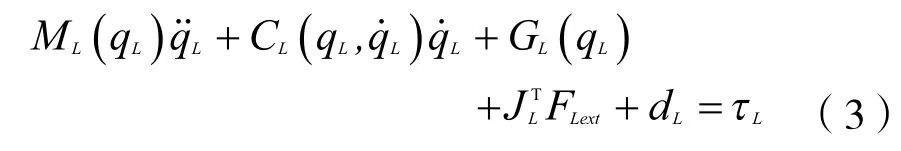
3.2 双臂运动学与动力学建模

手臂作为一个子系统，通过控制肩关节与肘关节的运动，使手臂末端到达期望位置。手臂的运动学与动力学分析在躯干坐标系中进行，其示意图如图3所示。

图3 以躯干坐标系为基坐标系的手臂简化模型

手臂正运动学方程为：

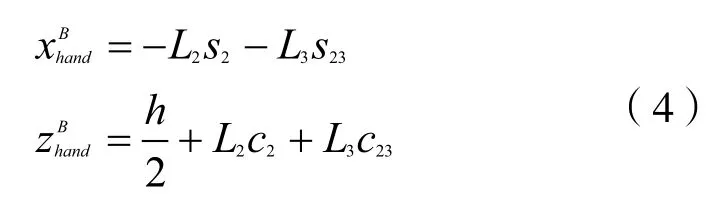
手臂雅可比矩阵为：

手臂总质心位置坐标为：

仍然采用拉格朗日方法建立动力学模型，并整理为如下标准形式

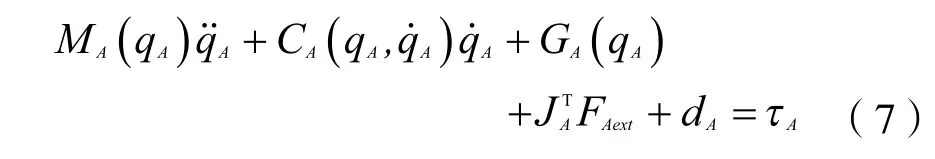
3.3 头部运动学与动力学建模

头部通过一个俯仰关节与躯干相连，作为一个子系统进行控制。在躯干坐标系中分析该子系统的运动学与动力学，如图4所示。

头部质心在躯干坐标系中的位置为：

头部子系统的动力学描述为：

图4 以躯干坐标系为基坐标系的头部简化模型

3.4 倒立摆运动学与动力学建模

虚拟倒立摆子系统是最为重要的一个子系统，它是保持机器人平衡的关键，是实现机器人整体运动的基础，其简化示意图如图5所示。考虑到机器人采用分块控制，利用双腿、双臂以及头部运动学计算出位于躯干坐标系中虚拟质心的位置

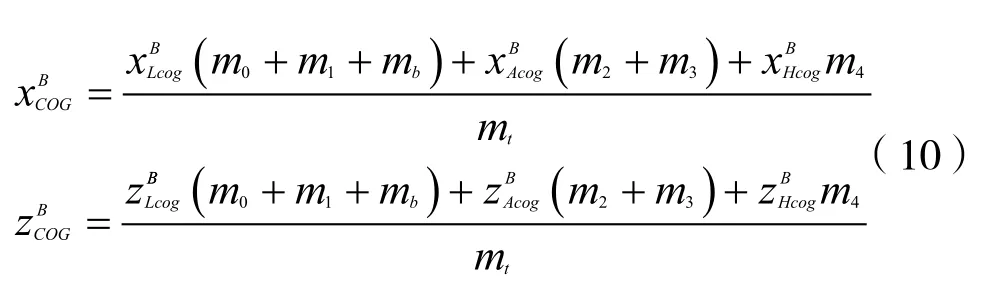
坐标系{oB}到{ow}的齐次变换矩阵为

此时，将身体各个连杆的质心集中于一点，作为一级倒立摆的虚拟质心，在轮轴坐标系中对虚拟质心位置进行计算，利用公式（13）和公式（14）得到轮轴与虚拟质心之间的连杆长度及虚拟俯仰角。

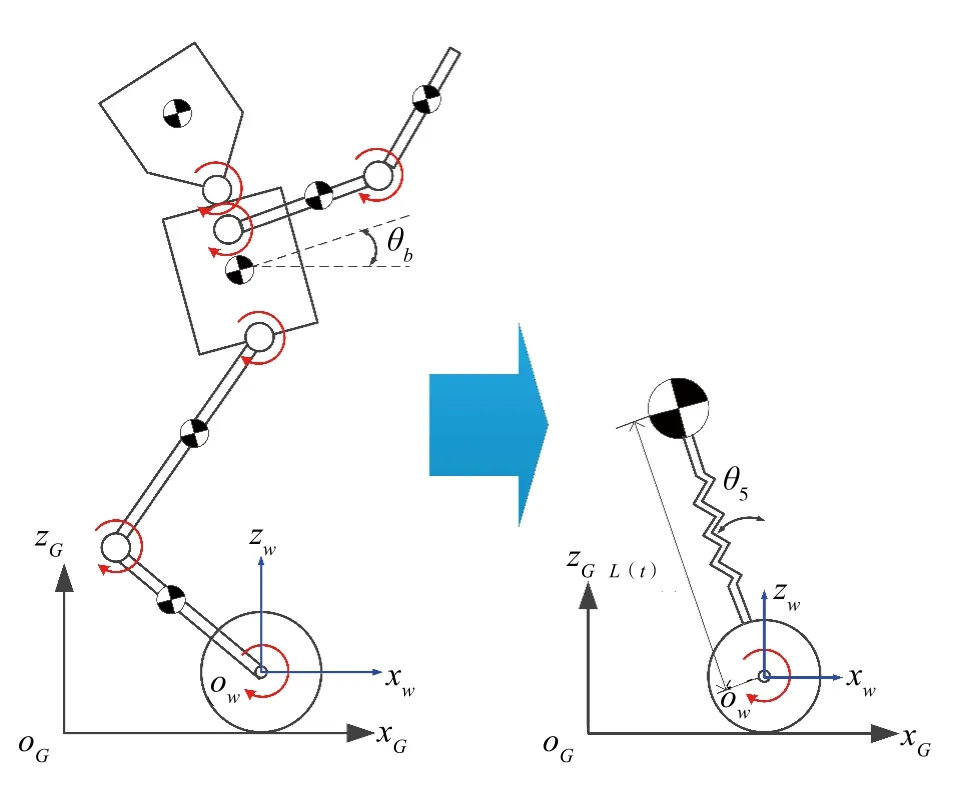
图5 机器人简化为虚拟倒立摆模型

假设该虚拟倒立摆的驱动轮始终与地面保持接触，并且不产生滑动，其运动学满足：

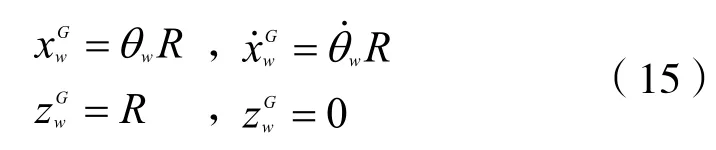
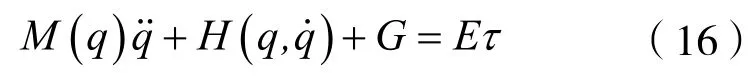
假设该虚拟倒立摆的驱动轮始终与地面保持接触，并且不产生滑动，根据运动学关系得到如下三个非完整约束：

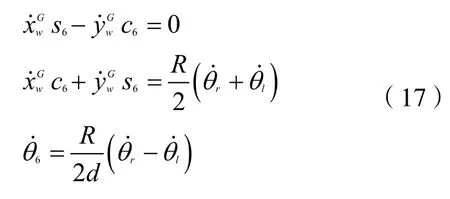
为得到这一约束方程组的零空间，即公式（17）的可行解空间，首先将该约束整理为的形式，其中，

将该约束条件利用拉格朗日乘数法引入动力学方程，动力学方程变为：

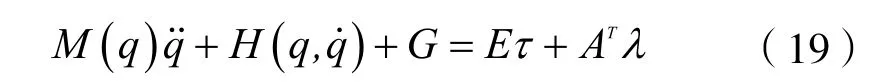
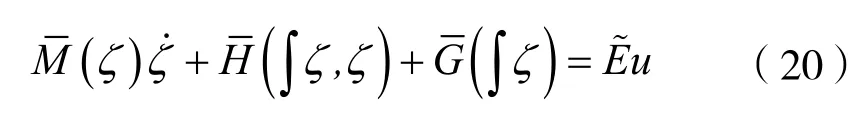
4 控制器设计

由于系统的自由度较高，整体动力学系统的建立非常复杂，并且不利于满足机器人控制的实时性。考虑到工程应用中对控制器执行性能的要求，本文将整体机器人系统分为三个控制模块，既相互独立又互相影响，其关系框图如图6所示。

4.1 腿部与手臂的控制

腿部与手臂的控制有许多相似之处，都为控制两个驱动俯仰关节使末端到达期望位置，本文对腿部与手臂的控制采用相同的控制器——加入前馈补偿的比例微分反馈线性化控制器。

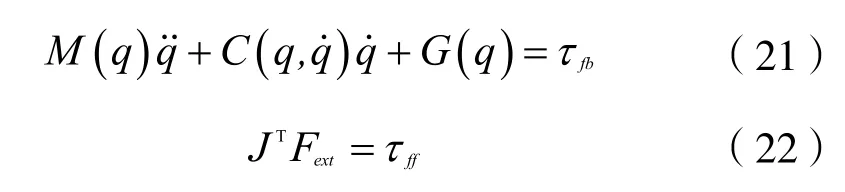
其中，τff为前馈力矩，τfb为反馈力矩。状态变量q为关节空间的变量，对于机器人腿与手臂的运动控制，运动聚焦在操作空间，因此期望值一般为末端位置，而不是关节角度值。利用公式（22）进行非线性状态坐标变换：

其中，p为末端位置坐标。解得：

图6 平台总体控制框图

将公式（25）、（26）带入公式（21）

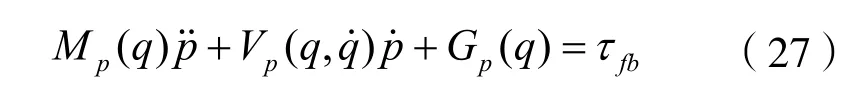
此时，式（27）的动力学系统状态变量为末端位置向量，输入仍为关节力矩。在此基础上构造控制器保证末端位置p、速度、加速度分别渐进收敛至期望位置轨迹pd、期望速度轨迹与期望加速度轨迹即

反馈线性化是处理非线性系统较为常见的一种控制方法，由内环控制率与外环控制率组成，内环控制率为：

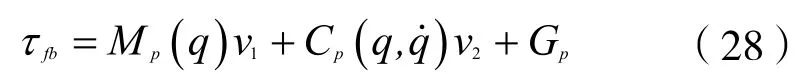
其中，v1，v2为外环控制率的输出：

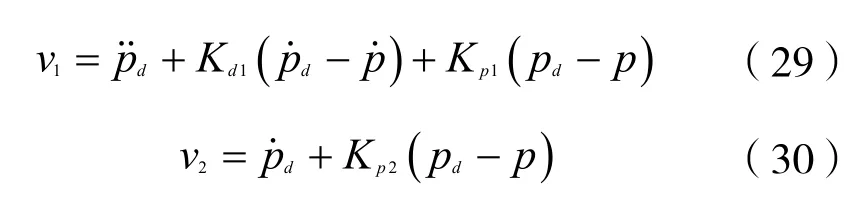
所提控制方法所产生的输入力矩为：

其控制框图如图7所示。

图7 腿部与手臂控制框图

4.2 虚拟倒立摆运动控制器

为推导方便，采用符号形式表示虚拟倒立摆动力学公式：

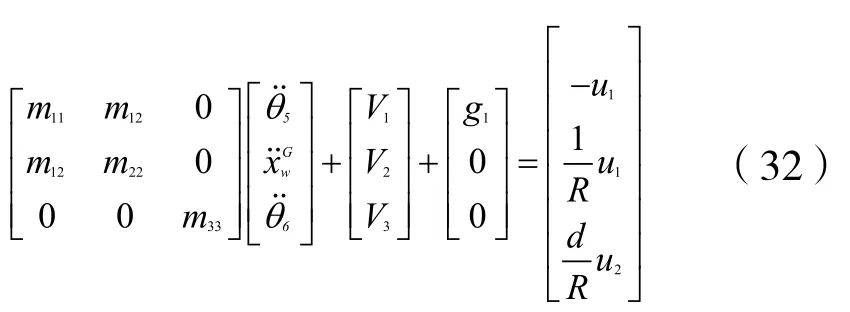
由公式（32）可看出子系统-5θ与子系统是耦合的，子系统-6θ则与另外两个子系统完全解耦。整理得到如下形式的动力学方程：

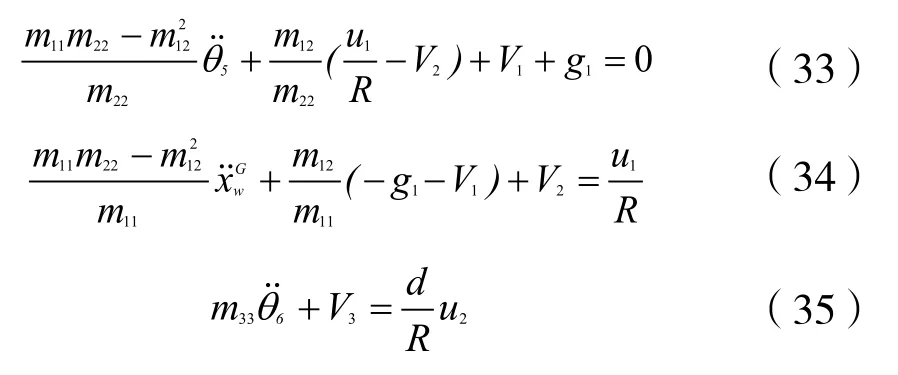
4.2.1 状态变量的获取

机器人利用三个传感器，分别为左右轮上的编码器与躯干几何中心处的惯性测量单元，获取左右轮弧度信息与躯干俯仰角度。通过运动学推导得到虚拟倒立摆的俯仰角与质心高度。但是该控制器中的状态变量不能由传感器直接获得，需要根据机体位置约束，利用传感器信息实时计算状态变量，其中，俯仰角5θ为计算得到，由5θ差分得到。其他状态量的计算如下：

其中，pc为机器人左右轮轮轴连线中点所行驶的总路程，对应地，为行驶速度。

4.2.2 控制器设计

分别给出俯仰角、俯仰角速度、偏航角、偏航角速度、小车行驶路程、小车线速度期望值θ5d、构造控制器，使得

设计一个PD控制器，两个PID控制器，分别对俯仰角、偏航角、小车路程进行控制。

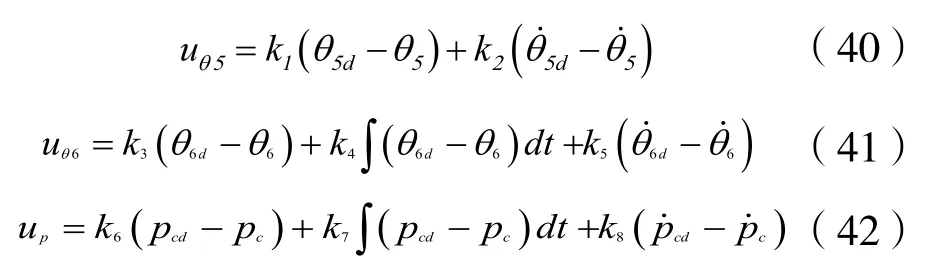
两个驱动轮的输入力矩为：

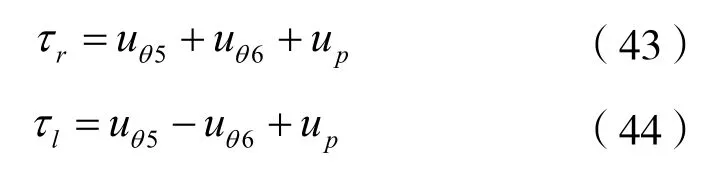
5 仿真实验

5.1 实验设置

本文提出的控制方法利用仿真软件Webots进行仿真，仿真软件运行环境为Core i7，采样时间为100Hz。仿真模型如图8所示，腿部两个俯仰关节、手臂两个俯仰关节以及头部一个俯仰关节处安装有位置传感器，驱动轮装有编码器，躯干的几何中心处装有惯性测量单元。为验证文中所提控制方法的有效性，分别进行了平衡实验、直行实验、转弯实验、姿态调整实验，并对数据进行分析。

5.2 平衡控制

图8 于Webots环境中搭建的机器人仿真平台

该机器人的控制模块中，作为其他控制模块的前提，最为重要的是虚拟倒立摆的平衡控制，为了验证所提方法的有效性与抗外扰能力，分别利用20kg的摆锤与70kg的摆锤垂直击打处于平衡状态的机器人后侧，选取增益分别为k1=-25，k2=-5，此时，机器人能够迅速回复到平衡状态而不会失稳。如图9所示，分别展示了初始俯仰角与俯仰角速度都为0时，受到20kg与70kg摆锤击打时，机器人恢复稳定过程中的虚拟俯仰角度与虚拟俯仰角速度曲线。可看出受到20kg摆锤击打时，虚拟俯仰角峰值达到11度，受到70kg摆锤击打时，虚拟俯仰角峰值达到25.6度，都能够在4s内恢复平衡状态，未出现震荡。

5.3 直线运动控制

在成功实现平衡的前提下，希望机器人摆脱遥控操作，摆脱对参考位置曲线、参考速度曲线的要求，到达期望位置的同时达到期望速度。首先，对直行运动进行实验，选取增益为k3=-0.06，k4=-0.001，k5=-0.23，只给出期望位置pcd=5，期望速度机器人由世界坐标系的原点出发，根据当前位置、当前速度，自主规划下一时刻速度，最终使得实验数据如图10所示，机器人自主规划平滑的速度曲线，先加速，后减速，当速度降为0时，恰好到达期望位置。由虚拟俯仰角曲线图可看出，机器人的加速度与俯仰角的方向和大小有关，当机器人虚拟质心前倾，存在前向加速度，且角度越大加速度越大，当机器人虚拟质心位于轮轴上方时，加速度为0，当虚拟质心后倾时，产生后向加速度。当机器人到达期望位置时，虚拟俯仰角恰好恢复到平衡位置，未发生抖动。

5.4 曲线运动控制

令机器人跟随一条曲线轨迹时，可将跟随任务分解为直行与转向，该实验结合上文中的直行控制器，验证航向角控制器的有效性。期望轨迹轨迹各点处弧度均不相同，其弧度曲线如图11（b）中的期望轨迹所示，航向角控制器增益为k6=65，k7= 0 .0075，k8=3.4。此时，机器人能够实现位置与航向角的同时跟随，由世界坐标系的原点处出发，实际运行轨迹如图12所示，左右轮的输入力矩如图13所示。

图9 机器人受到外力冲击时的虚拟俯仰角、俯仰角速度曲线

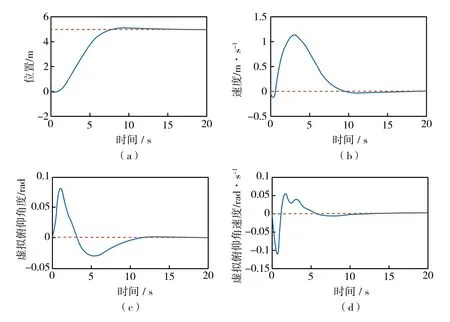
图10 机器人直线运动时的实验数据曲线

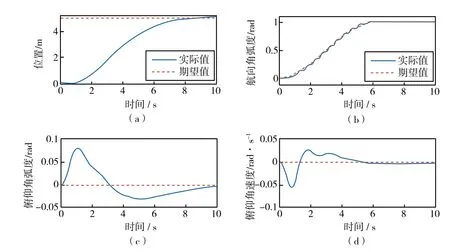
图11 机器人转弯运动的实验数据曲线

图12 机器人的行进轨迹曲线

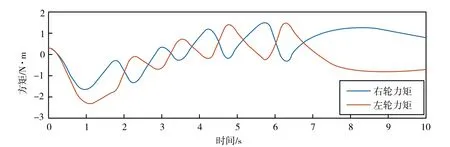
图13 左右轮力矩曲线

5.5 身体姿态控制

同时进行腿部、手臂位置跟随实验以验证所提控制器的有效性。本实验同时控制手臂末端与足端跟随规划的期望轨迹，规划、控制、数据收集均在躯干坐标系中进行；平衡控制器对腿部、手臂运动产生的虚拟质心前后移动所造成的机器人不稳定进行控制，对虚拟质心位置的计算在轮轴坐标系中进行；位置控制器保证了机器人姿态变化时的位置跟随能力，对机器人位置的数据收集在世界坐标系中进行。控制左右手臂、左右腿分别进行相同运动，且无外摆，因此，只对手臂末端与足端的前后位置与上下位置进行规划即可。手臂控制器的增益为Kd1=800，Kp1=1000，Kp2=3000，手臂末端初始位置为（0,0.8），期望位置为（0.5,0.1），对两点进行三次样条差值，得到图14 （a）、（b）中的期望轨迹。腿部控制器的增益为Kd1=900，Kp1=1000，Kp2=4000，足端初始位置为（0,-0.94），期望位置为（0.01,-0.6），对两点进行三次样条差值，得到图14（c）、（d）中的期望轨迹。图15（a）为虚拟倒立摆模型的身体质心位置曲线，可见身体姿态的变化引起虚拟质心的实时变化，由质心位置所计算出的虚拟俯仰角的曲线如15（b）所示，俯仰角的变化范围为［-0.015178，0.02756］rad，机器人处于稳定状态。其次，虚拟俯仰角的前后波动对机器人位置产生了影响，其变化范围为［-0.100366，0.288195］ m，处于允许范围。15（d）为同时保证机器人的平衡与位置轮的输出力矩曲线，变化范围为［-1.168327，1.681358］N·m。这一实验在验证了手臂、腿部控制器有效性的同时，也验证了平衡控制单元与位置控制单元的抗持续外扰能力。

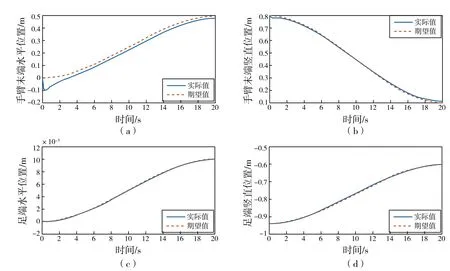
图14 手臂与腿部姿态变化曲线

图15 机器人姿态调节的相关实验数据曲线

6 结 论

本文提出一种腿-轮复合机器人，并对平台进行运动学、动力学建模与控制。考虑到整体建模与控制的复杂度，将平台分为手臂子系统、腿部子系统、头部子系统以及虚拟倒立摆子系统，构造基于笛卡尔状态空间的加入前馈补偿的比例增益反馈线性化控制器对手臂子系统与腿部子系统进行控制；将各子系统的质心映射为虚拟倒立摆子系统的杆件质心，并作为一级倒立摆进行控制，实现平台的前后移动与转弯运动。