主观题评分中的评分者漂移及其传统检测方法

赵海燕 辛 涛 田 伟

（1.北京教育考试院，北京 100083；2.北京师范大学心理学部，北京 100875；3.北京师范大学中国基础教育质量监测协同创新中心，北京 100875）

主观题作为一种重要的题目形式，由于形式多样、考查灵活以及能够探查考生深层次的能力，备受测验编制者和命题者的青睐，业已成为众多大型测验和考试的重要组成部分[1-2]。主观题评分通常先制订评分细则，再由评分员根据主观印象按照细则对行为样本进行评定。不管评定量尺建构得如何好，量尺信度仍然主要取决于进行评定的人，主观题最突出的构念无关变异主要来自于评分员[3]。研究表明，评分员自身在多次评分时难以保持一致，不同评分员对于相同行为样本的评分也不尽相同。评分员自身以及不同评分员间在多次评定上的不一致性,直接降低了结果分数的信度和效度,这种现象被称为评分者效应（rater effects）[4]。一段时间以来，研究者倾向于将评分者效应视为评分员固有的一种静态特征，不随时间、场合和任务发生改变，并以相同方式影响着所有被评价的行为样本。随着研究的深入，研究者逐渐认识到评分员的表现会随着时间、场合以及任务的变化而改变[3,5-6]，从而引起评分者效应的波动，即发生评分者漂移（rater DRIFT）。

一些大型测验机构和教育管理部门已经意识到评分者漂移的存在与危害，如美国教育与心理测验标准（The Standards for Educational and Psychological Testing）明确指出：测验实施者必须对评分员的表现进行实时监控，以确定是否存在评分者漂移，并在报告结果分数时要去除这种测验无关变异的影响[7]。评分者漂移的存在凸显了动态评估的重要性，为评分过程的质量监控提出了新的挑战。在此背景下，研究评分者漂移的模式、规律以及内在机制，深入挖掘评卷质量的发展与保持机制，不仅对评分过程的改进、有效监控机制的建立、评分员的遴选与评价的完善具有重要的实践价值，也能为补偿方案的制定奠定基础，最终有助于提升大规模考试的信度、效度与公平性。

评分者漂移属于新近出现的研究主题，对多数研究者而言比较陌生。有鉴于此，本文将重点介绍评分者漂移的定义、使用的指标与传统的检测方法，并对未来研究方向加以展望。

1 评分者效应及评分者漂移

1.1 评分者效应

研究表明，评分员的知识背景、综合能力、工作经验、情绪偏好以及疲劳程度等个人特征，均会对评分的精确性和客观性产生影响，从而导致评分者效应的出现[4]；在主观题和其他类似任务的评分中，评分者效应非常普遍，这些效应会随着培训与监控减弱，但不会完全消失[4,8-15]。

Scullen等认为，评分者效应是一大类效应，导致这类效应的系统变异与评分员在评定中的表现有关，与被试的行为无关[16]。评分者效应按表现与影响机制可细分为多个子类别。一般说来，最受关注的效应有严厉度或宽松度效应（severity/leniency）、不准确性效应以及评定量尺使用模式上的系统变异，如趋中效应（central tendency）和范围限制等[17]。

1.2 评分者漂移

在评分进程中，诸多因素都可能影响评分员的行为表现，其中包括个人因素、评卷环境的物理因素以及评分过程中的学习、质量监控和培训的延迟作用等。大规模考试的评卷过程短则持续数天，长则持续数个星期；影响评分表现的诸多因素都会随着时间、场合以及任务的变化而变化；相应地，评分员的表现也会发生改变[3]，从而引起评分者效应的波动，即评分者漂移。

评分者漂移的定义也随着研究进程的发展而逐渐演变。早期研究认为，评分者漂移源自于评分员使用评分细则的前后不一致[18]。随着研究的推进，研究者认识到评分员会“随着时间进程的推进逐渐地、或多或少地展示出评分者效应”，评分者漂移是“评分员随着评卷时间进程的推进所发生的在评分表现上的差异性变化”[19]。实际上，在Wolfe等的最初提法中，评分者漂移的英文名称DRIFT近似为Differential Reader Functioning over Time的首字母，意为评分员的跨时间功能差异[5]。评分者漂移也是多种评分者效应波动的总称，如严厉度漂移、不准确性漂移以及趋中效应漂移等。

评分员的严厉度水平会随着评卷进程的推进而变化：当评卷过程持续较长时间时，评分员的平均评定可能在今天与明天、上午与下午，甚至试卷批次间发生波动，即评分员表现出严厉度漂移[6]。趋中效应同样会发生波动：随着评卷进程的推进，一些评分员会更加频繁地使用量尺的中间类别，表现一种渐进的范围限制，即发生量尺类别使用的漂移[6]。不准确性效应也会随着评卷进程发生漂移：一方面，练习效应使一些评分员变得更加准确；另一方面，疲劳和厌倦也可能导致评分误差随着评卷进程的推进而上升。此外，一些评分项目还包含持续培训或阶段性校正，这些做法也会导致不准确性效应发生变化[20]。

评分者漂移领域最受青睐的是严厉度效应，大部分研究均针对该效应展开[3,18]。只有少数研究关注其他效应的漂移[6,21-23]。研究表明，即使在相同评分环境下，不同评分员的评分表现也会随着时间进程的推进出现不同的趋势。总的说来，研究者已经认识到了评分者漂移研究的意义与价值，并进行了一定规模的研究。这些研究的方法和结论对了解评分行为有所助益，尽管仍存在一些不尽人意之处。

2 传统的检测方法

早期研究多采用重复评定策略，借助评定间的分数变化、相关分析和方差分析探查严厉度的跨时间变化[24]。随后，Congdon等[3]基于多面Rasch模型（Many Faceted Rasch Model,MFRM）[25]和差异检验方法检测严厉度漂移；在此基础上，Wolfe等拓展了一个监控评分者漂移的通用框架，并用于检测多个效应的漂移[6,26]。此外，还有一些研究借助多水平模型检测评分者漂移[23,27-28]。下文着重介绍传统的检测方法。

2.1 监控评分者漂移的通用框架

Wolfe等提出的通用框架将评分者漂移的监控过程分为4个步骤：一是将评卷进程划分为时间片段，划分基于评卷进程的长度和内部特点，相应地可按星期、天，甚至小时进行划分。二是确定评分者效应的指标，计算各时段的指标值并进行基线比较或相邻比较。前者选择一个时段作为参照，探查评分员在参照时段和目标时段间的行为变化；后者则将某一时段与相邻时段进行比较，以侦测评分员在相邻时段间的行为变化。两者在本质上属于简单的差异显著性检验；当结果显示差异显著时，即认定存在评分者漂移。三是选择刻画评分者漂移的参照框架，可分为内部参照框架和外部参照框架。内部参照框架根据特定评分员与其他评分员的一致性程度来刻画其表现，适用于采用多重评定的评分程序；外部参照框架则根据评分员的评定与某外部标准（如客观题分数或专家打分）的一致性程度来刻画其表现，适用于采用单一评定的评分程序。四是决定是否采用锚定策略以及是否使用全部数据建立链接。使用外部参照框架时，要采用锚定策略，即用外部指标固定某些参数值。若不采用锚定策略，则要使用全部数据建立量尺标度[6]。

2.2 多面Rasch模型及其变式

传统Rasch模型可视为包含两个面：个体能力和题目难度。事实上，个体在主观题上的得分不仅取决于其能力和题目难度，还受到评分员严厉度和题目特定等级难度等因素的影响。有鉴于此，Linacre将传统Rasch模型拓展为多面Rasch模型。基础的多面Rasch模型中只加入了一个评分员侧面，其数学表达式为：

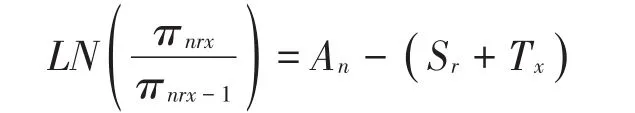
其中，πnrx和πnrx-1分别为个体n被评分员r评为等级x和x-1的概率；An为个体n的能力水平，即在潜在能力连续体上的位置；Sr为评分员r的严厉度；Tx为等级x相对于等级x-1的难度或阈限位置。

多面Rasch模型有几种变式可用于处理评分者漂移。第一个变式中加入了一个时间侧面，故称为时间模型（the time facet model）[25]，可用于探测评分员在不同时段间的整体变化。要直接估计评分员个体在每一时段的水平，则要用到分离模型（the separate model）[25]。时间模型也可以进一步扩展为交互作用模型（the interaction model）[25]，模型中加入了评分员和时间的交互项，表示评分员在每一时段对其总严厉度的偏离。

多面Rasch模型自诞生以来，广泛用于主观题的分数等值、评分者效应侦测、题目审定过程的质量监控和考试公平性研究等领域[2,8-9,11-13,20,26]。在评分者漂移的传统检测方法中，多个指标直接源自或部分基于多面Rasch模型。

2.3 静态评分者效应的指标

2.3.1 严厉度效应

当评分员打分具有持续低于或高于个体真实能力水平的倾向时，就表现出严厉度或宽松度效应[9,11,29]。对严厉度效应的定义通常处于一定的测验理论框架下。如在项目反应理论框架下，严厉度或宽松度效应被定义为：相较于其他评分员，目标评分员一致地给出偏低或者偏高的评定的倾向，前提是考虑该评分员所评的特定行为样本的水平[13,20]。严厉度效应的度量可直接使用经典测量理论框架下的平均数，当然这只作为一种粗略的度量；更常见的做法是从评分者模型中直接获得严厉度估计，大多数评分者模型均直接给出了严厉度参数，如多面Rasch模型的Sr等。

2.3.2 趋中效应

范围限制是指评分员未能使用整个量尺，将评定限制在量尺的某个范围或区域内[12,29]。当分数聚集在量尺中部时，范围限制一般也被称为趋中效应，趋中效应是范围限制的一个特例[12,29]。趋中效应并不影响量尺中段评定的准确性和有效性，但会导致低端被试能力的高估和高端被试能力的低估。与严厉度效度不同，趋中效应在多数评分者模型中并没有直接指标，研究者为此开发了若干导出指标。

探测范围限制和趋中效应，最简单的指标是原始分的标准差或方差[30]。一般说来，分数向平均数集中且标准差较小意味着存在趋中效应[31]。

多面Rasch模型的常用估计程序FACETS[32]给出的均方拟合指标（fit indexes），也可用于探测趋中效应。均方拟合指标相当于卡方统计量除以自由度，取值范围为0～+∞。均方拟合指标的值在0.50～1.50[10]或0.60～1.50[33]表明拟合度可以接受。当存在趋中效应时，拟合统计量明显小于1[31]。

基于模型考查趋中效应还可计算残差与期望值的相关（the expected-residual correlation，rres,exp）[4,31]。残差与期望值的相关被称为残期相关；当存在趋中效应时，残期相关为负，趋近于-1；当存在极端化倾向（趋中效应的反面）时，残期相关为正，趋近于+1[4]。类似指标还有残差与模型分的相关（the correlation between ratee measures and modelbased residuals，rres,score）。残差与模型分的相关被称为残模相关，同样可作为趋中效应指标。二者的区别在于分数的单位，期望值的单位为logit，模型分的单位则为原始分数单位[31]。

2.3.3 不准确性效应

不准确性效应指评分员的评分与个体真实能力间看似随机的差异与分歧[4]。通常，评分者效应强调对评分误差的均衡的系统性贡献；与此不同的是，不准确性效应属于非均衡性误差，可以因时间、特质、群体、被评价个体的不同而异[12]，实际上对效度构成更大的潜在威胁[8]。评分情境下的诸多因素均会导致不准确性效应出现，如评分员对测验的内容背景了解不充分，评分前未经过充分培训，具有不可改变的偏见等，主要原因都是评分员未掌握评分细则[31]。

不准确性效应同样可借助残期相关进行侦测。Wolfe指出，当存在趋中效应时，残期相关为负向；当存在不准确性效应时，残期相关接近零[4]。度量不准确性效应还可借助一个基于原始分的指标：他评相关，即与其他评分员给分的相关（rSR-ROR）。相较准确性较低的评分员，准确性较高的评分员的他评相关指标应更高一些[12]。与他评相关类似的指标是原模相关[31]，即评分员所给原始分数与模型估得的个体能力分数间的相关（the score-measure correlation或the point-measure correlation，rscore,measure）。较高的正的原模相关说明评分员给分与被试能力估计间具有较强的一致性[31]。此外，均方拟合指标可说明评分员能否对行为样本进行可信区分，因此可同时作为趋中效应和不准确性效应的指标。这两个指标的期望值均为1，大于1表明变异大于预期，即存在不准确性效应[33-34]。

2.4 严厉度漂移检测方法

传统方法检测严厉度漂移，首先要基于分离模型或交互作用模型[30]拟合得到分时段的严厉度指标，然后对不同时段的指标进行差异检验。

当基于分离模型拟合数据时，可计算标准化差异指标（Signed Area Index,SAI）探查严厉度漂移[6,35]，用公式表示为：

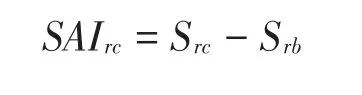
其中，SAIrc表示标准化差异指标；c为待比较的时段，b为基线时段;Src和Srb指评分员r在时段c和b的严厉度估计。SAI的显著性检验主要借助Z检验[6,35]，用公式表示为：

其中，ZSAIrc表示标准化差异指标的检验值和表示在时段c和b的评分员严厉度估计的方差。ZSAIrc的正值表示评分员变得严厉，负值表示变得宽松。计算出ZSAIrc后，可将它与标准正态分布直接比较。一些学者建议将它看作效果量指标（effect size indicator），数值大于0.50表示效应有意义[36]。

拟合交互作用模型得到的交互项估计Irt可直接作为严厉度漂移指标，表示评分员在每一时段的严厉度对其自身平均严厉度的偏离。对该指标可进行Waldt-test检验，零假设为评分员在时段c对其总严厉度的偏离为0。当样本足够大时，可以将t值与Z分布直接比较，t值计算公式表示为：

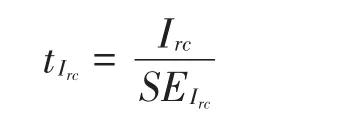
一些研究使用标准化差异指标探查严厉度漂移[15,18]。这个指标的主要不足在于其分布未知。大多数研究者假设，在零假设条件下标准化差异指标服从标准正态分布[3,15,18]。另一些研究使用交互项指标探测严厉度漂移[3,38]。此外，还有些研究对上述两个指标进行比较，但并未得出一致结论[6]。

2.5 均方类指标检测方法

评分员所给分数的标准差或方差可作为趋中效应的粗略指标。比较评分员在不同时段所做评定的方差，可用来说明是否存在趋中效应漂移。方差的比较一般采用F检验，指标计算公式表示为：

当存在趋中效应时，源自FACETS程序的均方拟合指标一般小于1。若评分员出现趋中效应漂移，均方拟合指标也会相应变小。因此，均方拟合指标在统计上显著降低将指示这种量尺类别使用上的变化。均方拟合指标近似符合卡方分布除以自由度，那么，两个均方拟合指标的比值应近似地符合F分布，自由度分别等于各自的自由度。检验值计算公式表示为：

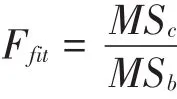
其中，MSc和MSb分别为时段c和时段b的均方拟合指标。评分员变异性的跨时间下降将导致均方拟合指标的数值随之下降，即Ffit小于1[6]。此外，Ffit还可以用作不准确性漂移的检测指标，检验原理与指标计算公式相同。

2.6 相关系数类指标检测方法

在评分者效应的指标中，多个均为相关系数，如度量不准确性效应的他评相关[12]和原模相关[31]、度量趋中效应和不准确性效应的残期相关[4,31]以及度量趋中效应的残模相关[31]等。对于这类指标，要先将相关系数转化为Fisher-Z函数，再进行Z检验。如对于他评相关，转换公式与检验指标计算公式表示为[6]：

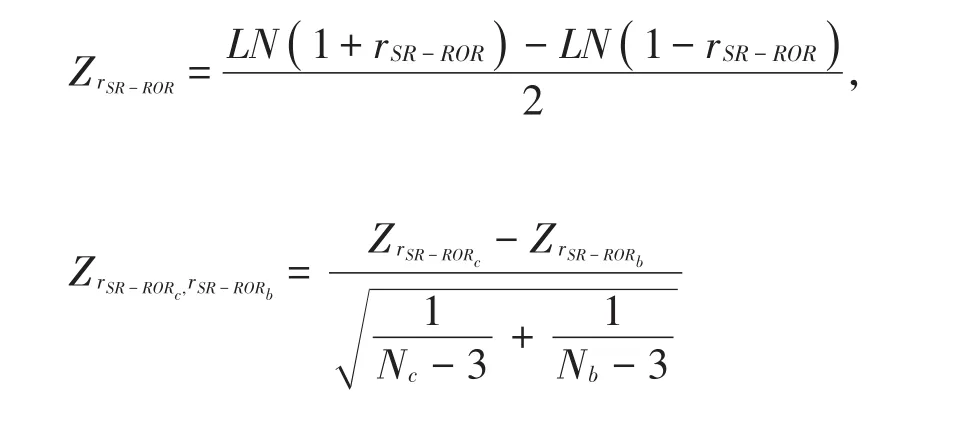
其中，ZrSR-RORc与ZrSR-RORb分别为在时段c和b的他评相关的Fisher-Z函数转换值。Nc和Nb分别为ZrSR-RORc与ZrSR-RORb所基于的评定数。其他几个相关系数类指标的检验同理。

利用差异检验法侦测评分者漂移，优点是简单明了，可以遵循现成的统计原理；不足在于每次只能比较两个时段，难以纵览评分者漂移的全貌。此外，当划分时段较多时，比较数量也随之增加；多重比较的Ⅰ类错误率也会相应地呈指数增长。在这种情况下须对Ⅰ类错误率进行校正[27]。

3 结束语

针对评分者效应和漂移，前人做了大量的研究。这些研究着眼于诸多评分者效应，基于不同的研究方法，在一定程度上揭示了评分者效应和漂移的机制以及负面影响。令人遗憾的是，评分者效应和漂移领域的大部分研究均针对有限的评分周期、有限的评分员样本以及有限的评分者效应展开。

结合现有研究的不足，对未来研究的可能方向加以展望：

首先，评分者效应和漂移领域目前大部分研究均采取心理测量取向，重视评分者模型的开发，并不关注效应产生的认知过程。事实上，研究评分者效应和漂移，除了心理测量取向外，还可以着眼于认知过程，通过构筑认知模型，厘清评分过程中的不同要素的作用及关系[14,17,39]。在评分者效应领域，两个取向的研究目前基本处于分离状态。然而，评分行为的外在表现和内在认知过程是难以分割的有机整体。只有将认知过程和心理测量有效融合，才能真正揭示外在差异背后的深层次心理原因，从而实现对评分者效应和漂移的有效鉴别与控制，最终保证行为表现测量的信度、效度和公平性。

其次，评分者效应和漂移研究方法相对单一，过于倚重差异检验方法，并未考虑多重评分策略导致的数据层级性。多次差异检验不仅易导致I类错误率增加，而且很难反映评分员的整体趋势变化。目前，评分者漂移的研究主要基于多面Rasch模型和差异检验方法。传统方法有其优势，也存在明显的不足。相较而言，借助适合数据结构特点的多水平模型侦测评分者漂移，不失为一种可行方法。评分者漂移在测量领域并不属于热点主题，目前多水平方面的应用尚处于起步阶段，在效应变量的选取、时间变量的加入、模型的细节设置方面都有待深入研究。这些探索将有助于提升评分者漂移检测的效度和效率。

第三，评分者效应的大部分研究、评分者漂移的绝大部分研究均针对严厉度效应进行，只有极少数研究关注其他效应[6]。而且，大多数研究均基于英语作文评分背景下的有限评分员样本，严重制约了结论的外部效度。不仅很少有研究关注高利害性大规模教育考试的真实评分过程，而且较大样本的多种评分者效应的整合研究在国内外都是稀缺的。事实上，统计无法从根本上消除评分者效应和漂移。对于评分者漂移的调控，认识到其存在以及危害性仅仅是一个开端，更重要的是从评分设计入手，在评分过程中寻求解决方案。研究评分过程和评分设计的改进，在研究设计上要综合考虑各方面因素，加入足够的评分员变量，综合多种评分者效应，实现对评分过程的全面刻画。在此基础上采取恰当的统计解决方案，才能在效应发生后进行有效的事后补救。