“篮球圈的秘密”项目式学习的实践与思考
□ 姚江峰
项目式学习是以问题为导向的学与教的方式,主要是导引学生对真实世界的、复杂的问题(任务/主题)进行研究,以小组合作的方式制订实施计划并进行实践探索,通过信息收集、调查研究、分享讨论,最终解决问题或完成作品。项目式学习活动通常持续时间长,更具挑战性和开放性,能有效促进学生深度投入学习活动,能有效实现知识的综合运用,积累问题思考和问题解决的经验,提升学生的动手能力、计划以及执行项目的能力、团队合作能力、创造力和领导力,促进终身学习技能的获得和综合素养的发展。下面以“篮球圈的秘密”为例来谈项目式学习的设计与实施。
一、提出研究问题
为了让项目式学习的内容更贴近学生的生活和兴趣,同时也为了充分利用教材内容作延伸和拓展,在学生学习“确定起跑线”这个教材内容之后,向学生提出这样的问题:通过“确定起跑线”的项目研究,我们发现了跑道起跑线中蕴藏的数学秘密。那你们还想研究体育运动中哪些隐藏的秘密?
“一问激起千层浪”,学生纷纷寻找体育运动中自己感觉疑惑的地方。通过思考和讨论,同学们提出了以下这些问题:“为什么跑道两边直两头圆”“排球网的高度”“身高与跳高的高度关系”……笔者把它们一一罗列在黑板上,并组织大家一起思考和讨论。最终,有一个问题引起了大家的共鸣和浓厚的研究兴趣。“为什么足球小网框很大,但篮球大篮圈却很小?”通过对问题的进一步梳理,最终把项目研究的焦点指向“篮球圈的秘密”:篮球和篮球圈的大小有什么关系?

【感悟与思考】
在平时的教学中,教师总是绞尽脑汁地寻找作为学生数学项目式学习活动的好材料、好内容。其实很多数学项目式学习的好材料和好内容就藏在教材之中,也可以利用教材之中的内容作再次延伸和拓展。本次项目式学习的案例是从教材“确定起跑线”一课的内容出发,通过“你们还想研究体育运动中其他哪些隐藏的秘密?”问题,趁热打铁,触发学生的热情和兴致,拓展学生的思维,再通过对学生问题的梳理归纳提炼,得到了本次项目式学习的主题:篮球圈的秘密。
二、项目方案设计
环节1:分组讨论制订项目研究预案
“篮球圈的秘密:篮球和篮球圈的大小有什么关系?”如何展开研究?请学生以四人小组为单位设计一份切实可行的研究方案,研究预案要求体现怎么想、怎么做的基本研究思路。
环节2:分组展示项目研究预案
各组到讲台前展示并说明自己组的预案,其他组进行提问。各组在展示预案时,要体现怎么想、怎么做的基本过程。
环节3:项目研究预案的调整
通过各组预案的展示和讨论,通过逐步筛选辨析,大家觉得下面两个组的方案比较好。

小组A:我们认为,要想知道篮球和篮球圈的大小有什么关系,可以从数据出发去思考并解决,用工具软尺先分别测量出篮球和篮球圈的周长,然后通过对两个数的比较,算出篮球和篮球圈的大小关系。小组B:我们认为,篮球和篮球圈的大小应该有一定关系,这个关系可以通过数据测量计算得到。但我们还思考:为什么会有这个关系?其他关系可以吗?为此,我们想通过不同大小篮球圈和不同大小篮球的投篮,通过命中率的收集与分析得出更有说服力的联系。
教师见学生基本已经对本次项目式学习的研究内容有了一定的了解,但还不是很清晰,于是,教师伺机进行引导:这两个小组从不同的角度思考得到了不同的方案,都非常好。第1个小组站在数据关系角度去思考设计,这虽然是我们大多数数学项目式学习的常用思维,但确实能够发现一些现象本质。而第2个小组,不仅想得到结论,还想追问结论后面的缘由。其实,通过刚才展示讨论,同学们已经逐步清晰了“篮球圈的秘密”项目式学习主要研究的两大内容:1.篮球圈的秘密,即目前我们采用的篮球圈和篮球大小的关系;2.“秘密”的缘由,即我们为什么采用这样的关系,是否可以有其他不同的关系替代。
在此基础上,教师引导学生对这两个小组的方案进行整合优化,形成一个项目式学习的研究方案(如下)。

【感悟与思考】
常规的数学教学往往比较重视解答现有的数学问题,即课本上已经经过数学处理的问题。学生只要按照学会的解题方法,一步一步地去解决就可以了。在不断反复操作下,学生虽然能熟练地掌握各种题目的解题技能、技巧,但一碰到实际生活,特别是项目式学习这种开放度较高的学习方式时,往往显得不知所措,无从下手。项目实施方案的设计是项目式学习成功的重要环节。本次项目案例采用了先分小组进行开放式预案的设计,然后通过小组展示说明和其他小组质疑提问等方式不断深入,最后结合该项目内容特点,制订统一的实施方案。这种从开放式预案到统一性方案的过程是项目式方案制订的较好路径,也是比较适合小学生开展数学项目式学习制订方案的一种方式。
三、项目研究的实施
以8人小组为单位,按照上面的统一研究方案,分场地进行实施。然后进行小组展示。(教师可以为学生开展研究活动提供必要的材料支持)
四、项目研究的展评
每个小组派两名代表进行展示,主要展示实践过程及得到的数据和结论。其他小组进行比较和提问,评选优秀展示小组。
环节1:“篮球和篮球圈的直径和面积大小关系”的研究成果汇报。
小组A汇报:
我们小组采用软尺去测量周长的方法,分别得到以下测量结果(注:篮球周长是指它的最大截面圆的周长;篮球面积是指它的最大截面圆的面积,下同):
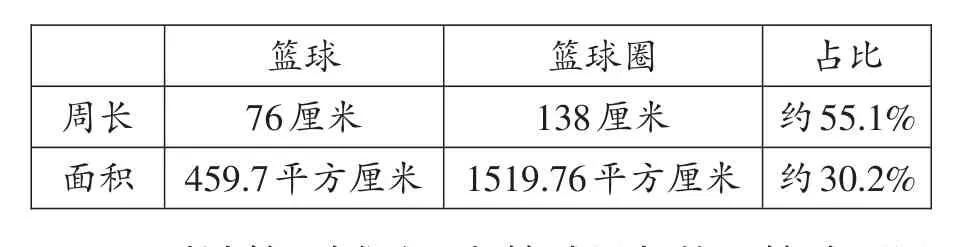
周长面积篮球76厘米459.7平方厘米篮球圈138厘米1519.76平方厘米占比约55.1%约30.2%
通过计算,我们得到:篮球周长约是篮球圈周长的55.1%;篮球最大的横切面面积约是篮球圈面积的30.2%。
小组B汇报:
我们小组采用直尺去测量周长的方法(先用线绕一周,再拉直用直尺测量),分别得到以下测量结果:

周长面积篮球81厘米530.66平方厘米篮球圈142厘米1603.8平方厘米占比约57%约33.1%
通过计算,我们得到:篮球周长约是篮球圈周长的57%;篮球最大的截面面积约是篮球圈面积的33.1%。
小组C汇报:
我们小组没有采用其他组的用软尺去测量周长的方法,而是采用网络资料检索的办法得到数据。因为,我们觉得软尺测量会有一定的误差。通过网络查询得到几组数据:
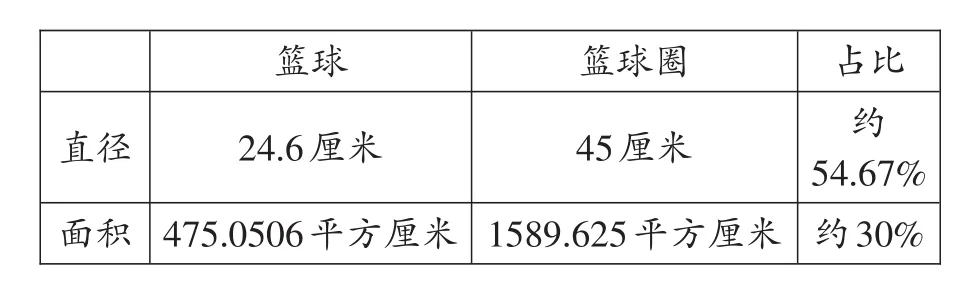
直径面积篮球24.6厘米475.0506平方厘米篮球圈45厘米1589.625平方厘米占比约54.67%约30%
通过上面数据,我们得到:篮球直径大概是篮球圈直径的54.67%,也就是一半稍微多点。篮球最大的截面面积约是篮球圈面积的30%。

教师伺机进行引导:刚才几个小组展示了他们第一步的研究结果,看到这几组同学的结论,你们想说什么?
生1:为什么他们的数据都不一样,到底哪一组比较准确?
生2:我发现虽然他们的数据不一样,但结论其实差不多,都是篮球周长约是篮球圈周长的一半多一点;而篮球最大的横切面面积是篮球圈面积的30%左右。
师:对于生2的发现你们同意吗?
生:同意。
师:通过不同方式的测量虽然数据不太一样,但结论比较接近,我们都发现了篮球圈的秘密:篮球最大的横切面面积约是篮球圈面积的30%。为你们的发现点赞。
师:那么,刚才生1提到的,你们有什么想说吗?
生:这个其实我们以前也经历过,虽然大家测同一条线段、同一个角,但往往全班同学测量的结果会有很多种。我觉得这可能是测量时的误差导致了结果不一样。
师:她说的你们同意吗?(生表示同意)
师(追问):那么这几个小组,你们觉得哪个小组的结果更精确一点?为什么?
生:我觉得网络查询得到的数据应该更精确点,因为这些数据往往是专业人员测量出来的。
师(小结):在思考篮球和篮球圈的大小有什么关系这个问题时,有的小组采用了实际测量,有的小组通过网络查询资料的方式,都得到了篮球和篮球圈的相关数据,并通过数据发现了篮球和篮球圈大小的关系,给了我们数据上的更直观感受。刚才讨论时说用工具实际测量会产生比较大的误差,确实我们刚才也看到几个小组的结果不一致,有的相差还比较大。那么实际测量是不是就一定不好呢?其实实际测量只要操作得好,不仅能够得到精确的数据,还能够培养我们认真、细致、规范的品质。当然,我们有时也可以向刚才这个小组的同学一样,充分利用资料检索的方式,通过检索得到我们需要的数据,但也需要考证数据的真实性与准确性。
环节2:“同圈异球”和“同球异圈”两种方式投篮命中率研究成果汇报。
在这一环节的研究中,教师为学生提供了以下材料:在“同圈异球”的实践中,采用了同一规格标准篮球圈,并分别选取标准篮球、5号足球、皮球,它们与篮球圈的面积占比分别为30%、23%、10%。在“同球异圈”的实践中,我们采用标准篮球投篮,而篮球与三种篮球圈的面积占比分别为50%、30%、10%。通过学生的分组实践,具体结果如下。
小组A汇报:
我们小组对“同圈异球”和“同球异圈”两种方式进行投篮命中率的数据收集,8位同学每人都分别投了5次,具体命中率结果如下表:
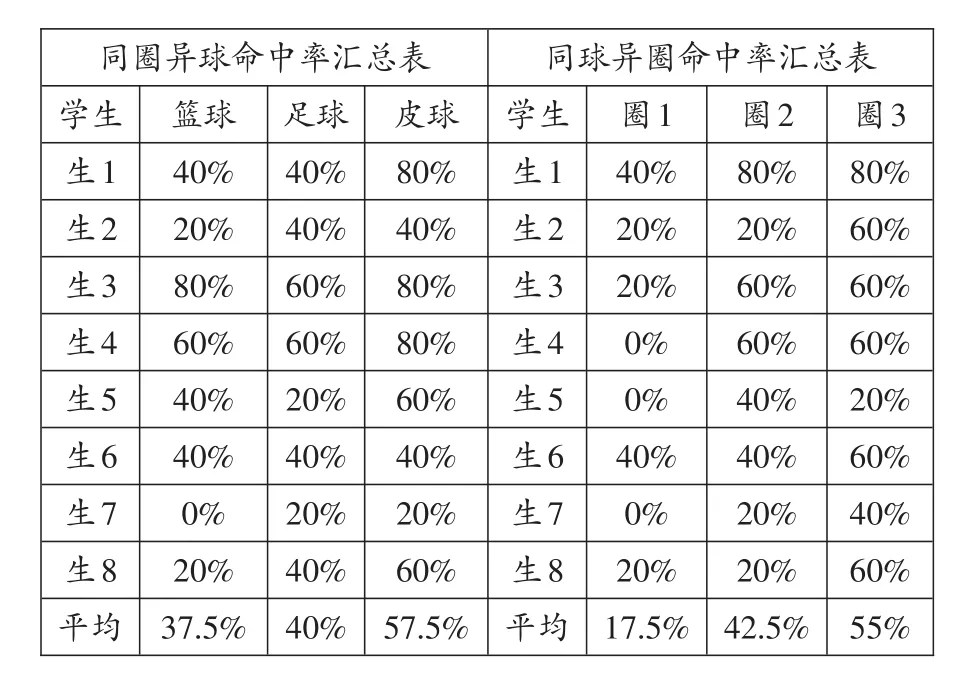
圈3 80%60%60%60%20%60%40%60%55%同圈异球命中率汇总表同球异圈命中率汇总表学生生1生2生3生4生5生6生7生8平均篮球40%20%80%60%40%40%0%20%37.5%足球40%40%60%60%20%40%20%40%40%皮球80%40%80%80%60%40%20%60%57.5%学生生1生2生3生4生5生6生7生8平均圈1 40%20%20%0%0%40%0%20%17.5%圈2 80%20%60%60%40%40%20%20%42.5%
根据命中率计算我们发现:无论是“同圈异球”还是“同球异圈”,命中率随着球与篮球圈的面积占比大小而改变,占比越大命中率越低,占比越小命中率越高。
小组B汇报:
我们小组对“同圈异球”和“同球异圈”两种方式进行投篮命中率的数据收集,5位同学每人都分别投了5次,具体命中率结果如下表:

圈3 40%20%20%40%40%32%同圈异球命中率汇总表学生生1生2生3生4生5平均篮球40%20%0%20%20%20%足球40%20%20%0%20%20%皮球60%40%60%40%20%44%同球异圈命中率汇总表学生生1生2生3生4生5平均圈1 20%0%0%0%0%4%圈2 20%40%20%0%20%20%
我们的发现跟前面这组差不多,无论是“同圈异球”还是“同球异圈”,命中率随着球与篮球圈的面积占比越大命中率越低,占比越小命中率越高。同时我们还发现,这个规律大部分同学是这样,但有些同学不是这样。
小组C汇报:
关于方案第二步用“同圈异球”和“同球异圈”两种方式进行投篮命中率的数据收集,我们小组经过商议,选取组内日常投篮命中率特别高、中等、较低的3个同学作为代表来投篮,分别是表格中的生1、生2、生3。因为老师以前说过,在选取样本的时候,要具有代表性。投篮命中率在日常就差异很大,如何得到具有代表性的数据,投篮的人也要有代表性。我们小组3位同学每人都分别投了10次,具体命中率结果如下表:
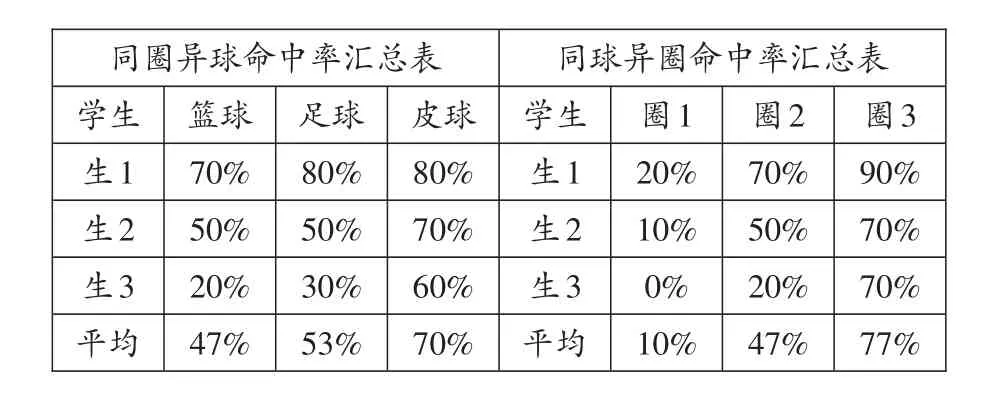
圈3 90%70%70%77%同圈异球命中率汇总表学生生1生2生3平均篮球70%50%20%47%足球80%50%30%53%皮球80%70%60%70%同球异圈命中率汇总表学生生1生2生3平均圈1 20%10%0%10%圈2 70%50%20%47%
研究结论:通过表格中的数据我们可以发现,在“同圈异球”中,当占比为23%时,命中率随之有变化,但不是很大。但当占比为10%时,命中率明显提升。这个现象在“同球异圈”的实践中依然如此,当占比为50%时,看似提高不多,但命中率急剧下降,但当占比为10%时,命中率明显提升。这个现象在平时水平特别高的生1身上也许不明显,但在平时水平较低的生3身上差异显著。以上是在我们六年级学生身上,如果放到大人身上,占比的细微变化也许命中率就会有大的变化。因此我们认为,国际通用的篮球与篮球圈面积占比为30%具有一定的道理。
教师小结引导:刚才几组汇报结论都差不多,但具体实施时还是有差异的,有的小组8个人都投了,有的5个人,有的才3个人,有的投了5个,有的投了10个。你们觉得都可以,还是哪一组比较好?
生1:我觉得都可以,因为从这几组结论看,都差不多。
生2:我觉得第3组比较好,他们虽然只选了3个人,但这3个人具有很强的代表性。
生3:我同意刚才同学的意见,第3组的比较好,第1组虽然样本大,但不一定科学。第3组虽然样本小,但比较科学。刚才我看到第2组汇报时,有时候单个同学的命中率变化并没有符合我们的结论,甚至相反。有可能是这个同学本身投篮命中率非常不稳定。
师:刚才几个同学讲得都很有道理。确实,在研究的时候,我们不仅要注意样本的数量,还要注意样本的代表性。在这次的研究中,日常投篮命中率会对我们的测量结果乃至结论产生很大的影响。假如某个小组,平时都不是很喜欢篮球,投篮命中率都极差,那有可能导致命中率全部为0,那么对结论的推导就失去意义了。
师(追问):刚才我们都同意合理的样本数和样本代表的典型性,会使得到的数据在差异上和说服力上更强,同时,得到的结论也增强了可信度。刚才第3小组只选了3名代表,分别投了10次,是否够了?如果不够,我们可以怎么做?
同学们被老师这么一问,都纷纷陷入沉思,并且争论开了。
生1:投10次还不够,可以投50次。
生2:我觉得不行,1个人投太多后面命中率会越来越差。
生3:我觉得我们几个小组都可以模仿第3小组的方式,都选3个有代表性的,都投10次,然后把各个小组的数据汇总在一起,这样,样本数和样本代表性都兼顾到了。
【感悟与思考】
项目式学习有助于知识在数学中应用、在生活实践中得以验证、得以完善,有助于学生实践能力、创新能力等的培养。但对于小学生而言,其自身储备的数学知识还比较少,数学思维能力还比较弱,对像这样比较复杂的项目式学习本身具有畏惧情绪。因此,在日常的数学项目式学习实施后的评价中,我们不能过于关注结果正确与否,而要关注学生在项目式学习过程中的参与度、思维度。特别要关注学生在开展项目式学习时采用的方法,因为研究方法的合理选择及运用是今后开展研究性学习的基础能力。本项目学习过程中,教师非常注重研究方法的评价。比如前面方案设计时是采用工具实物测量周长的方法,但有的小组采用了网络检索数据的方法,教师在讨论中一方面给予肯定,同时也引导学生思考实际测量和网络检索两种方法的各自功能。在实施方案第二项研究中,教师在肯定前面几组的汇报时,对考虑投篮学生样本代表性选择的小组进行了重点点评和肯定。这样更侧重研究方法的评价应成为学生数学项目式学习的重要方向。

