动载作用下复合型裂纹扩展的近场动力学模拟
钱 剑, 姜冬菊, 龚 庆, 黄 丹*
(1.河海大学 工程力学系,南京211100;2.重庆市质量和标准化研究院,重庆400020)
1 引 言
工程构件中往往存在初始裂纹等缺陷,其中复合型裂纹较为常见。复合型裂纹的扩展规律和扩展过程模拟,尤其是动载作用下的扩展过程模拟,一直是研究的难点。为了探索含复合型裂纹构件的裂纹扩展过程与破坏机制,国内外学者开展了大量相关理论、试验和数值研究。John等[1]通过混凝土梁冲击试验研究了复合型裂纹动态扩展路径以及初始裂纹位置对破坏路径的影响;Carmona等[2]通过试验分析了配筋对钢筋混凝土梁裂纹扩展的影响及其破坏机理。各种新型数值方法也应用于含复合型裂纹构建的动力破坏过程模拟,Song等[3]应用基于虚拟结点的有限元法模拟了三维圆盘冲击梁的破坏,得到了裂纹扩展路径和裂尖扩展速度;章青等[4]基于广义扩展有限元法进行了复合型裂纹扩展分析。此外,Zhang等[5]应用晶格胞元模型分析了动载作用下裂纹扩展速度和扩展时间与初始裂纹长度的关系。
近年来,基于非局部思想建模的近场动力学PD(Peridynamics)方法[6,7]以其在模拟不连续力学问题方面的独特优势而日益受到关注。早期的单参数常规键型PD本构模型[7]在应用时受到诸多限制,Gerstle等[8]考虑物质点对的旋转,提出了PD微极模型。另一方面,文献[9,10]在常规PD本构模型中引入可以反映长程力尺寸效应的核函数修正项以提高定量计算精度,并应用于混凝土构件的冲击破坏模拟[11]。黄丹等[12-14]进一步改进和讨论了核函数修正项的作用。
本文基于PD微极模型引入能反应长程力尺寸效应的核函数修正项,构建计算精度更高的双参数微极模型和相应的粒子系统动力加载算法。通过模拟动载作用下含复合型裂纹混凝土三点弯梁的破坏过程,并与试验结果对比,对模型和算法进行验证。在此基础上,分组模拟分析了动载作用下复合型初始裂纹位置、长度和方向对三点弯混凝土梁破坏模式、破坏时间与承载能力的影响。
2 模型和算法
将固体离散为空间域内一系列包含所有物性信息的物质点。如图1所示,对空间域R内任一物质点x,在其邻域范围δ内的任一点x′与x之间的相互作用力为
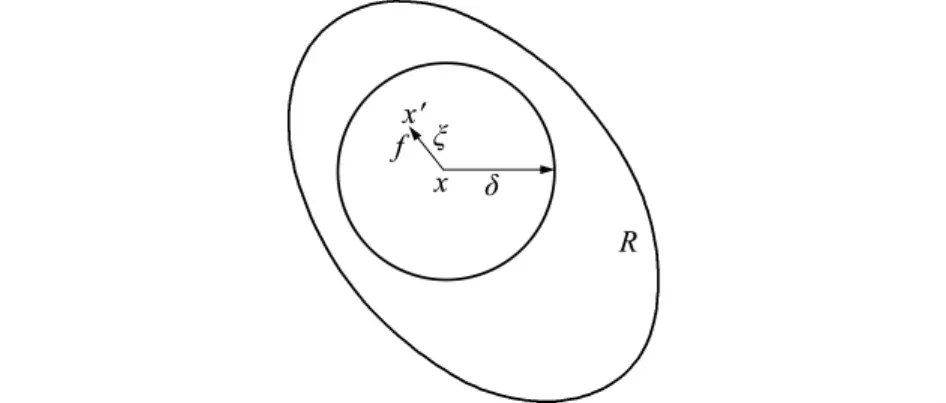
图1 物质点间相互作用Fig.1 Interaction of material points
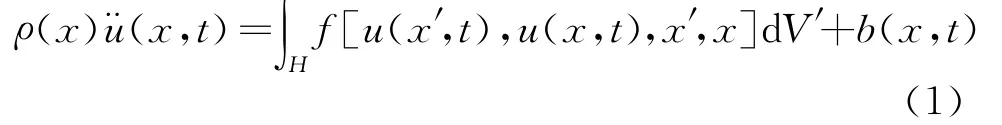
式中ρ为材料密度,u为物质点位移,x为物质点的位置,b为外力密度。
若物质点间的作用力与时间历史无关,则有

式中η和ξ分别为物质点相对位移与相对位置。
若将物质点间的作用力视为一种中心弹簧[15]作用,可引入物质点对的势能密度
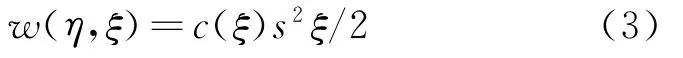
c(ξ)为物质点对的拉伸微模量系数(类似于中心弹簧的拉伸刚度),s1为物质点对的伸长率。本构力(点对力)可表示为
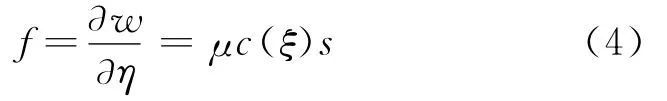
以往近场动力学模拟中应用最广泛的是常规微弹脆性PMB(Prototype Microelastic Brittle)近场动力学本构模型,其微模量c通常通过与传统弹性理论中的应变能等效[16]:
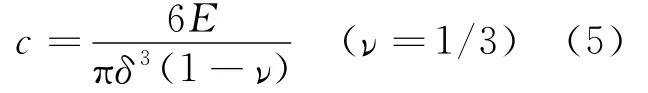
常规PMB模型在求解平面应力问题时受到泊松比ν=1/3的限制[16],为突破该限制,Gerstle等[8]引入物质点对的转动自由度,得到PD双参数微极模型。应用应变能等效可计算出平面应力问题的微模量系数为

式中c为拉伸微模量系数,d为弯曲微模量系数。ν=1/3时,d=0,模型退化为PMB模型。
若进一步引入能够反映长程力尺寸效应的核函数修正项g,则PD物质点点对势能为

核函数需满足长程力随物质点对变化规律,其选取准则如下[9]:

式中 Δ(ξ)为Dirac Delta函数。经试算比较,根据式(8)取g=[1-(ξ/δ)2]2,由上述应变能等效原理,可求得平面应力问题的微模量系数为

对于物质点xi近场范围内的任一点xj,式(1)的离散形式可表示为
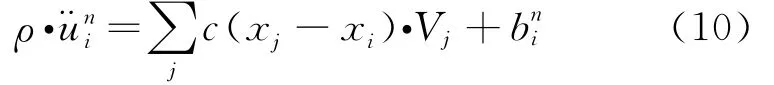
式中n为时间步数,对于平面问题,Vj=。针对动力问题,本文应用显式差分求解,采用中心差分格式,通过自主编写的Fortran语言程序实现。给定模型的初始状态(位移u、速度u·和位置x),经过迭代,记录每一步循环物质点的速度、加速度和位移等变量,更新物质点所在位置和所受合力,从而完成计算。
3 动载作用下复合型裂纹扩展模拟
3.1 模型验证
为了验证核函数修正项对计算精度的提高作用,对相同参数的模型,分别用本文模型、不含修正项的微极模型和有限元方法进行模拟比较。模型参数如下,材料弹性模量E=31.37GPa,泊松比ν=0.2,密度ρ=2400kg/m3,fc=41MPa,ft=3.19MPa。梁上侧中点受集中动荷载P作用,加载速率为4×107N/s。模型尺寸如图2所示。
如图3所示,取梁下边界点1ms时的y方向位移作为参考对象,对比无核函数、含核函数和FEM结果可知,加入核函数修正项后,梁下边界y方向位移(即梁下边界挠度)更接近有限元解,说明核函数能有效提高计算精度。下文计算均使用该模型。
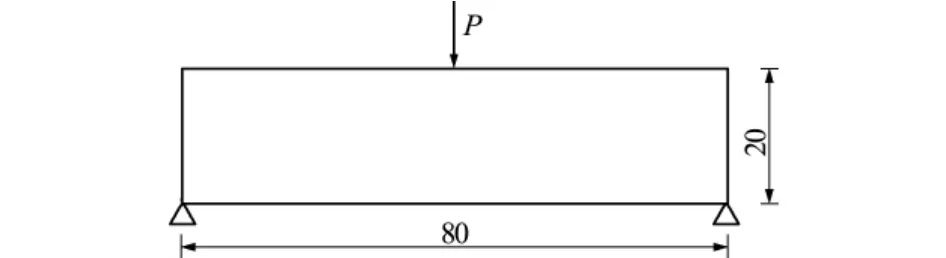
图2 验证模型Fig.2 Test model
John等[1]开展了动荷载作用下含复合型裂纹混凝土三点弯梁的破坏试验,得到含不同裂纹位置的三点弯梁破坏模式与破坏路径。为了验证本文模型和算法应用于模拟动载作用下复合型裂纹扩展路径的可靠性,采用与文献[1]相同工况进行模拟。模型相关尺寸如图4所示,其中L=0.063m。材料参数与上文一致。近场动力学模拟中物质点离散间距Δx=4mm,时间步长取5×10-7s,s0=1.02×10-4(本文临界伸长率均取s0=ft/E)。与试验工况一致,梁上侧中点受集中动荷载P作用,加载速率为4×107N/s。
图5为本文模拟得到的裂纹起裂和扩展路径。可以看出,裂纹从130μs起裂,至173μs整体破坏。本文所得裂纹起裂角为60.66°(与水平方向夹角),与John等[1]试验观测(60°)结果吻合较好,如图5(b)所示。裂纹贯穿时,起裂点与裂纹终点的连线与水平面的夹角为44.69°,如图5(e)所示,与图5(f)试验结果[2]及图5(g)中扩展有限元模拟结果[4]均吻合较好。结果表明,应用本文的粒子类模型和算法能较好地模拟动载作用下复合型裂纹扩展全过程。
3.2 初始裂纹位置的影响

图3 三点弯梁挠度Fig.3 Deflection of three-point bending beam

图4 三点弯梁动载模型(单位:mm)Fig.4 Three-point bending beam model under dynamic load(unit:mm)
为研究裂纹初始位置对含复合型裂纹三点弯梁破坏模式及其承载能力的影响,取含垂直裂纹混凝土梁参数与John等[1]的试验一致,如图4所示,变化初始裂纹位置分别取L/s=0.0625,0.1172,0.1406,0.1484,0.25和0.5(s为支座间距),对应的裂纹扩展路径如图6所示,均与John等[1]的试验结果吻合较好。
可以看出,随着初始裂纹位置的变化,三点弯梁的破坏主要有两种模式。当裂纹在支座附近时,梁中心产生新裂纹并扩展,初始边裂纹不扩展;当初始裂纹离开支座一定距离时(考虑单边情况,L/s约为0.1172~0.5,单裂纹在梁的另一侧时结果对称),沿初始裂纹裂尖向加载点附近扩展。
图7为含不同位置初始裂纹混凝土梁的动力破坏时间比较。可以看出,当初始裂纹趋于两端的支座附近时,由于要在跨中新形成裂纹并沿新裂纹裂尖扩展,梁的承载能力较高。当初始裂纹离开支座一定距离,偏向跨中加载位置时,沿初始裂纹裂尖起裂,破坏时间随着裂纹靠近梁跨中而提前,表明梁的承载能力较低,与实际情况吻合。L/s=0.1484~0.25时,梁的承载能力下降明显;L/s=0.25~0.5时,梁的承载能力变化不明显,但整体承载能力非常低,在0.5时承载力最低,此时直接由裂纹垂直向上方加载点快速扩展,与实际情况相符。

图5 裂纹扩展过程Fig.5 Crack propagation process
3.3 初始裂纹长度和方向的影响
工程中常见含不同长度和不同方向的初始裂纹,影响梁的破坏过程和承载能力。本节对含不同初始长度和不同初始倾角的裂纹进行分组模拟和分析,得到其扩展路径、裂纹起裂与完全破坏时间。
为提高计算效率,三点弯梁取长为0.8m,高为0.2m,下边界存在预置裂纹,裂纹初始长度为l,均匀离散间距 Δx=2mm。L/s=0.2143,0.3571,l/h=0.1,0.2,0.3(h 为梁高),α =30°,60°,90°,120°,150°(α为裂纹方向与水平向左方向的夹角),其余参数均与3.2节一致。
图8为L/s=0.3571,l/h=0.3,α=30°,60°,90°,120°,150°时的裂纹扩展路径。其他情况下的裂纹扩展路径与该图一致。可以看出,动载作用下初始裂纹的扩展均由裂尖开始,向加载点附近扩展。裂纹起裂角约为60°~70°,最后的破坏路径与水平方向夹角约为45°~57°。
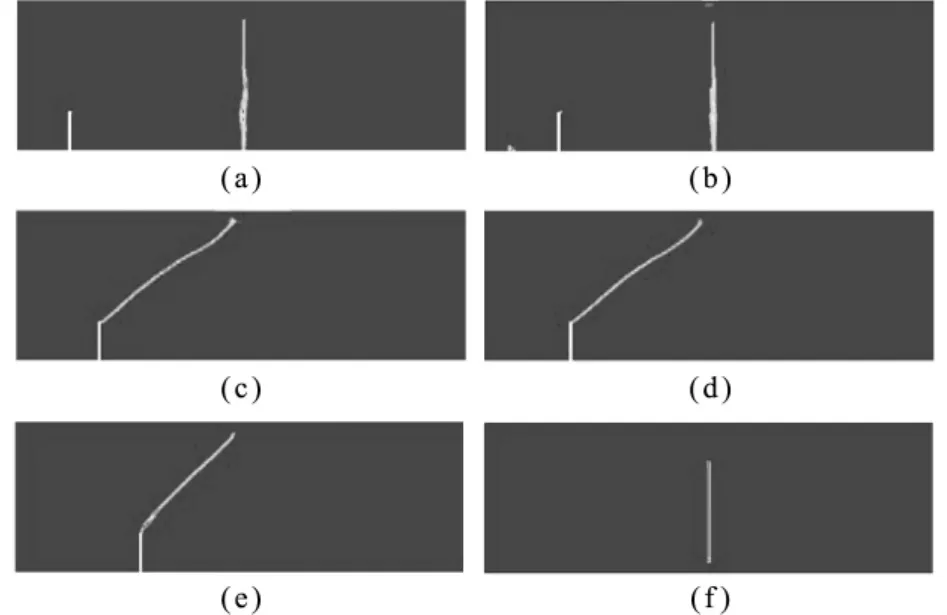
图6 含不同裂纹位置的裂纹破坏模式Fig.6 Failure mode with different positions of crack
表1为裂纹位置L/s=0.2143和0.3571两种工况下,含单一初始边裂纹的混凝土梁的裂尖起裂时间以及结构破坏时间(从开始加载至最后裂纹失稳扩展至上边界的总时间)随初始裂纹长度与角度的变化。由表1可知,无论初始裂纹位置如何,随着初始裂纹倾角的增大,起裂时间均先减小后增大(梁承载能力先降低后提升)。

图7 裂纹位置对破坏时间的影响Fig.7 Influence of crack location on failure time

图8 含缺陷三点弯梁的破坏模式Fig.8 Failure modes of notched three-point bending beam
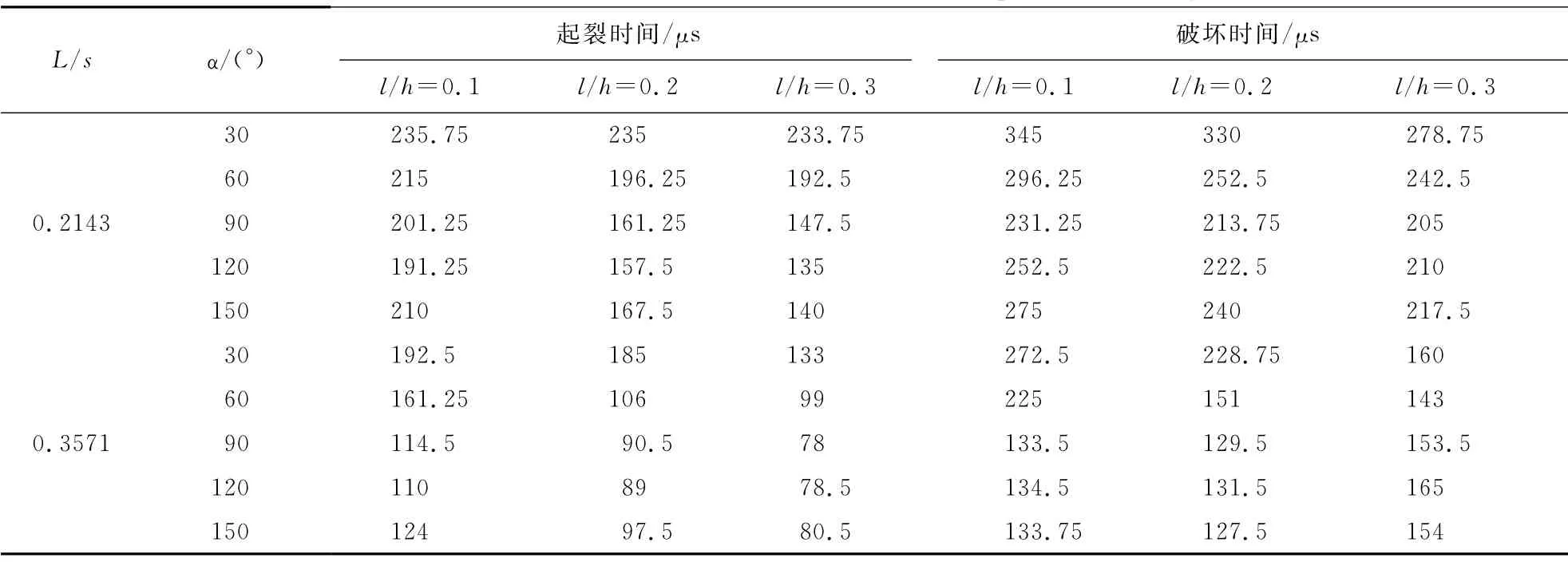
表1 三点弯梁起裂时间与破坏时间Tab.1 Crack failure and failure time of three-point bending beam
分析模拟几种工况的具体数据可知,当初始裂纹位置和长度给定而初始裂纹方向改变时,总是当α=120°时裂尖最先起裂,或与此时该裂尖最靠近动力加载点有关;而三点弯梁完全破坏(裂纹快速失稳扩展至上边界)最快的情况总是对应于α=90°时,说明虽然α=120°情况裂尖最先开始起裂,但α=90°情况裂纹扩展更快。
此外,初始裂纹方向对裂纹扩展起裂角和扩展路径也有影响。裂纹扩展方向均从裂尖指向加载点附近,起裂角为60°~70°,破坏路径与水平方向夹角为45°~57°;当初始裂纹偏向其所在梁一侧的支座时,承载能力明显高于偏向于跨中一侧的情况。
裂纹位置对扩展过程的影响与3.2节结论一致,在各种给定初始长度和倾角的复合型裂纹情况下,当L/s增大,即初始裂纹位置更靠近跨中时,裂纹起裂时间和结构完全破坏时间均明显加快。
初始裂纹越长,起裂时间与破坏时间越短,表明梁的承载能力越差,符合实际情况。
4 结 论
(1)本文在常规近场动力学微极模型基础上,引入反映物质点间长程力尺寸效应的核函数修正项以提高计算精度,并构建相应粒子系统动力算法,通过模拟动载作用下含复合型裂纹三点弯梁的破坏过程,验证了本文模型和算法的适用性。
(2)通过模拟含不同位置复合型裂纹三点弯梁的动力破坏过程可知,三点弯梁中复合型裂纹的扩展主要有两种典型的模式。当初始裂纹位置靠近支座时,梁跨中产生新裂纹并沿新生裂纹裂尖起裂和扩展;当初始裂纹离开支座一定距离(单侧L/s约为0.1172~0.5)时,沿初始裂纹尖端起裂和扩展。此外,沿边裂纹裂尖扩展时,梁的承载力随着L/s的增大而显著减小,在L/s=0.5时最小。
(3)初始裂纹越长,起裂时间越早,梁的承载能力越低。初始裂纹方向主要影响裂纹扩展的起裂角和扩展路径,其起裂角为60°~70°,破坏路径与水平方向夹角为45°~57°;当初始裂纹偏向其所在梁一侧的支座时,其承载能力明显高于裂纹偏向跨中一侧的情况。以上边界中点受集中动荷载、下边界左侧含初始裂纹的三点弯梁为例,初始裂纹与水平向左方向夹角为120°时,裂尖最早起裂,但破坏最快的则总是在初始裂纹竖直的情况下。

