激光导航AGV的马尔可夫定位方法研究
李昊,叶文华,满增光
(南京航空航天大学 机电学院,江苏 南京 210016)
0 引言
自动导引车(automated guided vehicle,AGV)作为高端智能物流运输装备正越来越多地应用于自动化生产与制造中,定位问题是AGV导航运动中的基本问题。马尔可夫(Markov)定位算法是一种常用于初始位姿未知情况下的AGV全局定位方法[1]。该方法利用概率状态分布,将对AGV位姿的估计看作多阶Markov过程,离散化的空间位姿即代表其中的状态变量。Markov定位方法不仅可以解决AGV被移动到新位置而已知初始位姿错误的拐骗问题,而且可以处理多模及非高斯分布的概率模型。应用上,Markov定位方法可以基于任意一种形式的地图实现对AGV的全局定位[2]。对Markov定位的研究最早出现在基于拓扑地图的定位中[3],其后被广泛应用于基于栅格地图的定位。Markov定位方法最大的问题在于对移动机器人位姿的离散化处理导致的庞大计算量。在以往的研究中,Burgard等[4]利用图像处理中的八叉树模型使状态空间可变分辨率表示;吴庆祥等[5]通过对Markov定位的仿真研究,使用电子罗盘解决了对称环境中的定位问题。但针对计算量庞大限制Markov定位方法应用的问题,始终没有完善的简化改进方法。
Markov定位方法的庞大计算量主要体现在两方面[6]:离散化后的AGV位姿是三维变量,计算时离散化栅格数量多;计算某一时刻单一栅格信度时涉及到前一时刻所有栅格的信度。针对这两方面,本文采用高精度电子罗盘的方向信息作为AGV的姿态信息,从而将三维空间信息计算简化为二维平面信息计算;同时在计算Markov算法中的预测模型时通过傅里叶变换将空间域转换至频域,将AGV的两个平面位置变量视为一个整体处理,从而不必对相邻时刻的栅格信度重新依次计算,减少了计算量。将此简化预测模型计算方法结合观测更新模型构成Markov定位算法,从而实现对AGV的位姿估计与全局定位。
1 Markov定位算法
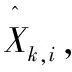
对全局定位问题而言,已知AGV的历史观测数据、运动控制输入和环境地图,k时刻AGV位姿估计可表示为:
p(Xk|Z0:k,U0:k,M)
(1)
其中,Xk表示k时刻AGV的位姿;Z0:k表示从0到k时刻AGV对环境特征的观测;U0:k表示从0到k时刻AGV所有运动控制输入;M表示环境地图,对于不同形式的地图有不同的表达形式。
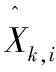
(2)
(3)
其中,η=1/p(zk|Z0:k-1,U0:k)为归一化常数,通过式(2)、式(3)的递归预测和校正递推计算可以对初始位姿未知情况下的AGV估计当前位姿,实现AGV全局定位。
2 基于降维和傅里叶变换的预测模型
由于观测校正更新式(3)的计算方法与地图形式息息相关且计算量在整个算法中不占主要构成,本文主要对预测更新式(2)进行简化计算量处理,主要包括对空间信息的降维及相邻时刻栅格的整体平移计算。
2.1 基于电子罗盘信息的降维处理
通过在AGV上安装高精度的电子罗盘,姿态分量φ可由方向信息直接得到,继而在计算中只考虑离散化后的AGV位置分量(x,y)的二维栅格信度,栅格信度计算的降维处理过程如图1所示。
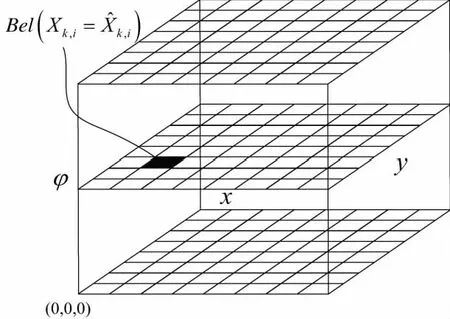
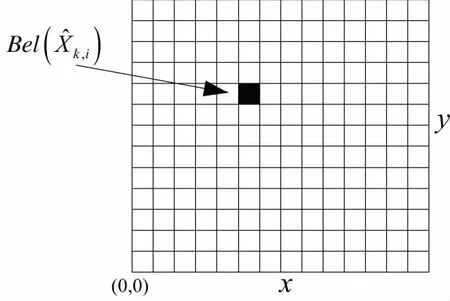
图1 栅格信度计算的降维处理
2.2 基于空间域-频域变换的预测模型
若把二维的栅格信度平面称为信度图像,将任一时刻的信度图像看作整体实现更新计算。即在得到运动输入uk后,同时考虑其不确定性,通过信度模糊化处理把k-1时刻的信度图像看作整体平移形成k时刻信度图像。
实际上在进行信度图像整体平移操作时,由于AGV运动的连续性,为避免导致误差的累积,需要实现信度图像的非整数倍单位栅格平移。本文采用基于空间域-频域转换的预测更新模型,同时也在频域中完成信度图像的模糊化操作。为此需要通过傅里叶变换转换信度图像,二维离散傅里叶变换公式可表示为:
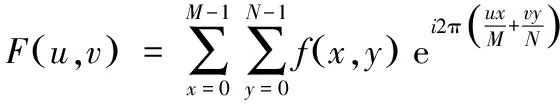
(4)
其中,f和F分别表示空间域与频域图像;M和N分别表示x与y方向的栅格划分数目。
空间域与频域中的平移关系可表示为:
f(x-x0,y-y0)⟺F(u,v)e-i2π(ux0/M+vy0/N)
(5)
其中,x0和y0分别表示空间域中信度图像的平移量,其可以是任意实数。
为实现信度图像的非整数倍栅格平移,基于式(4)和式(5),先将空间域中的f(x,y)转换至频域,得到F(u,v),利用傅里叶变换的周期性中心化F(u,v),利用卷积定理通过高斯低通滤波实现对栅格信度图像的模糊化处理,平移后的F(u,v)e-i2π(ux0/M+vy0/N)作为频域中新的信度图像再转换回空间域。


图2 基于傅里叶变换的预测模型
2.3 综合算法实现流程
基于降维和傅里叶变换处理预测模型的AGV马尔可夫全局定位综合算法实现如下:
k=0 ;

End
While TRUE
k=k+1;
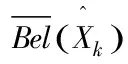
w=0;
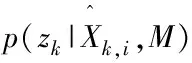
End
End
End
3 仿真分析
为验证本文提出的基于降维和傅里叶变换的预测模型计算方法的有效性和准确性,基于特征地图进行了复合环境中AGV运动的仿真。该仿真环境如图3所示,长宽均为30 m,设置50个特征点,其中49个特征点以均匀分布在环境中,构成相似性环境,以此验证算法的可靠性;第50个特征点使AGV在短暂的运动探测中能收敛到唯一位置。设置5个导航点A(0,-4),B(7,-4),C(7, 7),D(2.5, 7.5),E(-2.5, 5),AGV初始时刻位于第1个导航点(0,-4),初始朝向与初始运动方向均平行于x轴,最大线速度为1m/s,运动轨迹如图3所示。传感器及算法相关参数如表1所示。

图3 相似复合环境下所设置的环境特征地图

表1 相似复合环境中的AGV全局定位参数设置
仿真所得信度分布结果如图4所示。从图4(a)中可知,在初始k=0s时刻,AGV实际位置在(0, -4),经过计算各栅格被占有概率,得到了众多信度大值坐标点。由图4(b)可知,在k=5s时,AGV运动在AB段,得到相似环境中的若干对称位置。在k=12s时,AGV实际运动接近于导航点B,此时经过计算各栅格被占有概率,存在信度极大值的范围位置变为9个,AGV此刻的位置估计在这9个坐标附近。图4(c)-图4(f)显示了之后不同时刻AGV在概率栅格中的位姿信度极值分布和变化情况,在k=76s时,AGV探测到了第50个特征点,信度峰值极大值坐标收敛至一个,其他位置的概率信度均为0,即已经正确估计出了AGV位姿。从上述位姿信度的变化可知,随着AGV不断运动,感知到的特征信息不断增加,AGV从算法最初估计的多个坐标位置逐渐确定为唯一真实坐标。AGV位置估计与真实位姿的误差如图5所示,均控制在一个栅格大小以内。以上结果表明了AGV在相似复合环境中运动时,本文所提的基于高斯核函数的Markov全局定位方法在特征地图中是有效且准确的。
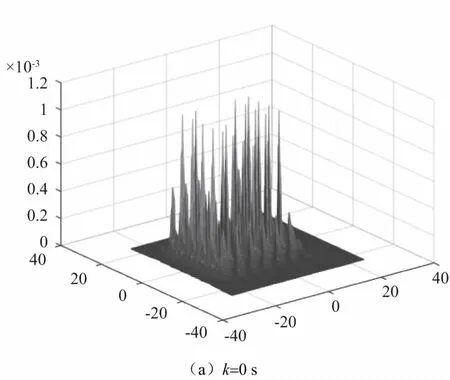





图4 相似复合环境下AGV直线行走仿真不同时刻信度分布图像
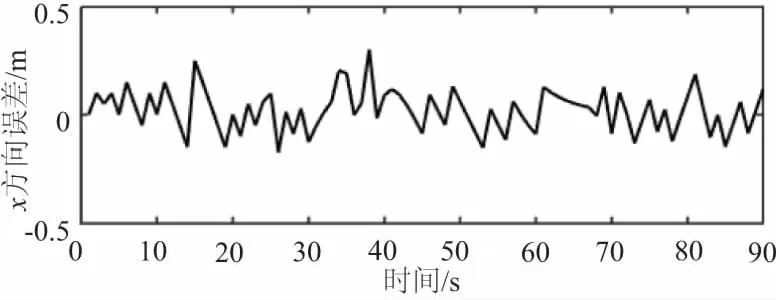
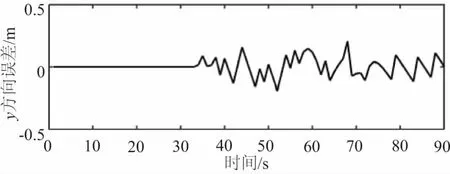
图5 AGV位置估计误差
4 结语
利用电子罗盘信息降低了求解AGV位姿信息的维度,且在计算Markov定位算法中的预测模型时利用频域变换将栅格信度视为整体计算,简化了信度更新时对相邻时刻栅格信息的依赖。加入预测模型新计算方法的Markov定位算法能有效运用在特征地图中对AGV的全局定位,不仅提高了Markov定位在特征地图中的实用性,也对其他类型的移动机器人和其他地图形式的定位需求提供了参考。

