基于泡沫铝芯材性能实验的夹层板抗侵彻数值研究

吴 捷，田阿利，任 鹏，姜文安，叶仁传，王明辉

(1. 江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003；

2. 武昌船舶重工有限责任公司，湖北 武汉 430060)

0 引 言

泡沫铝夹层板因其拥有质轻、高比刚度、高比强度和优越的吸能效率，在船舶与海洋工程、航空航天、建筑等行业得到了广泛的应用[1]。作为一种抗冲击复合结构，其不可避免地遭受各种弹体和砰击物的冲击。只有掌握其抗侵彻性能，才能使其充分发挥自身的防护能力。

目前，国内外专家和学者针对泡沫铝夹层板的侵彻性能问题，运用实验、理论分析以及数值模拟等方法展开了一些研究。Barnes等[2–3]对开孔泡沫铝材料在冲击下的破坏行为进行研究。Hou等[4]在准静态条件下对面板为金属铝，芯层为泡沫铝的夹层板进行实验研究，重点分析了侵彻速度、面板厚度、芯材密度和弹体头部形状对其抗侵彻性能的影响。Ghalami-Choobar等[5]通过理论和实验研究了子弹侵彻泡沫夹层板的动态响应，得到面板的裂纹分布和破坏模式。Feng等[6]对复合材料夹层板在低速侵彻下动态响应进行仿真，详细分析了闭孔泡沫铝夹层板在冲击下的层内损伤和层间损伤。D.D. Radford等[7]对泡沫铝为芯体夹层结构在冲击载荷下的数值模拟研究发现，泡沫芯体夹层板比相同质量的单层板具有更高的抗冲击性能，夹层板对冲击的阻力随着芯体厚度的增加而增加。Zhang[8–9]对面板为碳纤维聚合物、芯层为泡沫铝的锥形桁架结构夹层板在子弹冲击下的动态响应和破坏模式进行实验和理论分析。陈一鸣[10]研究了夹层板脱层对结构振动特性的影响。

综上所述，关于泡沫铝夹层板的侵彻实验、方法及理论虽已取得很大进展，但通过准静态试验参数建立相应的数值模型并对其做进一步系统深入的研究仍非常有必要。本文首先对闭孔泡沫铝材料在准静态条件下进行压缩实验，得到泡沫铝夹层板芯层的本构参数。基于泡沫铝本构参数和面板材料的本构参数建立了以Q235钢材料为面板，以泡沫铝材料为芯层的夹层板抗侵彻有限元模型。重点分析了半球形弹体载荷下的冲击过程、夹层板的塑性变形、能量吸收、剩余速度曲线以及弹道极限。展开泡沫铝夹层板抗侵彻性能相关参数研究，为夹层板在舰船结构应用中的优化设计及其抗侵彻防护提供参考。

1 夹层板材料力学性能实验

1.1 Q235钢面板材料性能

面板为Q235钢，其材料性能研究十分成熟，本构关系采用Johnson-Cook本构模型[11]，侵彻失效参数通过实验研究获得[12]，如表1所示。本文后续的研究，面板Q235钢材料参数均采用此表中的参数。

1.2 泡沫铝芯层材料性能

泡沫铝材料有不同的胞体结构类型、结构大小和结构形状，因此该材料没有统一的材料特性参数。本文考虑船用结构的特性，选用 4 种不同密度泡沫铝，开展了准静态压缩系列实验，建立可靠的泡沫铝压缩本构模型。

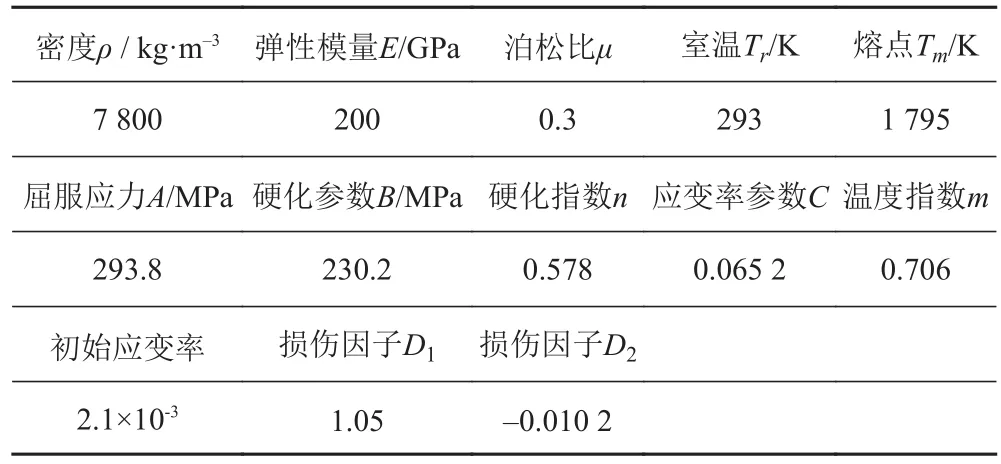
表 1 Q235钢的本构与损伤参数[12]Tab. 1 Material constitutive and damage parameters of Q235

1.2.1 试样设计

闭孔泡沫铝试样如图1所示，4 种密度分别为197 kg/m3，276 kg/m3，497 kg/m3和 541 kg/m3。由于泡沫铝的孔径较大，为了观测泡孔的变形，并消除尺寸效应，试样尺寸选为Φ30×30 mm，进行线切割加工后水洗烘干。

图 1 泡沫铝试样Fig. 1 Test specimens of aluminum foam

1.2.2 准静态压缩实验

实验主要由CMT5105型微机控制电子万能试验机及Power-Test试验软件完成，采用位移加载控制的方式，压载速率为0.5 mm/min。该加载速率条件下不同密度泡沫铝的压缩应力-应变曲线如图2所示。从图中可以看出，这种闭孔泡沫铝材料的压缩应力-应变曲线具有典型的三阶段特征，即线弹性阶段、屈服平台阶段和压实阶段。图3为闭孔泡沫铝的弹性模量与密度的关系。准静态压缩实验测得的泡沫铝芯材本构关系及其他力学性能参数，用于第 2 节有限元仿真计算中。

2 有限元仿真计算与结果分析

2.1 有限元模型

对钢-泡沫铝-钢夹层板结构建立1/4有限元模型，其中，板长为210 mm，宽为210 mm，芯层厚度为20 mm，上下面板厚度为0.4 mm。弹体材料为Q235钢，直径为12.62 mm，弹体形状为半球形弹体，质量为34.5 g。参考实验中保证弹体实际飞行姿态的弹体结构[13]，在有限元仿真中，将弹体的尾部挖去一个直径为6.2 mm，深度为10 mm的圆柱坑。为减少计算时间，子弹与泡沫夹层板的距离设定为0.1 mm。

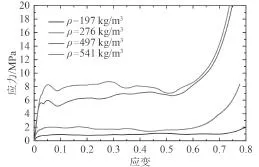
图 2 泡沫铝压缩应力-应变曲线（加载速率 0.5 mm/min）Fig. 2 Compression stress-strain curve of aluminum foam with different densities（loading rate: 0.5 mm/min）

芯层为闭孔泡沫铝材料，材料模型为*MAT_CRUSHABLE_FOAM（63#），材料参数选用上述准静态实验测得结果：密度为276 kg/m3，弹性模量为160 MPa，泊松比为0.20，屈服强度为2.01 MPa。

由于63#本构没有关于材料破坏准则和删除单元的算法，因此需要对其施加一个材料删除本构：*MAT_ADD_EROSION。选择最大塑性主应变失效，当其塑性主应变大于0.4时，其单元将会被删除[14]。

本文对泡沫铝夹层板侵彻仿真的网格划分采用分区划分的原则，分为侵彻区和非侵彻区，其中定义弹体两倍直径长度的矩形区域为侵彻区，在此区域进行网格细划，网格大小选为0.5 mm。非侵彻区域的网格大小选为2.0 mm。半球形弹体侵彻夹层板的有限元模型如图4所示。

根据实验工况，在外部边界上的所有节点设定为约束所有自由度，在模型的对称面上设定为对称边界条件。子弹和夹层板各部分的接触采用面-面侵蚀接触，面板与芯层之间的连接选用面-面固连失效接触。

图 4 半球形弹体侵彻夹层板有限元模型Fig. 4 Finite element model of sandwich plate impacted by hemispherical-nosed projectile

2.2 计算结果与分析

2.2.1 弹体侵彻过程

图5给出了半球形弹体以120 m/s的速度冲击夹层板时结构的变形和破坏过程。由图可知，夹层板的侵彻破坏过程可主要分为 3 个阶段：上面板的变形与破坏、泡沫芯层的变形与破坏、下面板的变形与破坏。

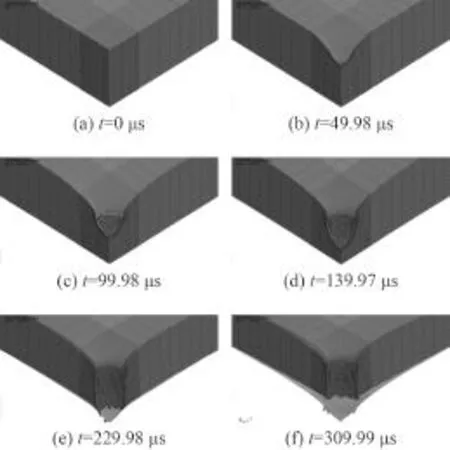
图 5 半球形弹体侵彻泡沫铝夹层板过程Fig. 5 Deformation of aluminum foam sandwich plates impacted by hemispherical-nosed projectile

半球形弹体侵彻夹层板时，夹层板结构的总体变形较小，主要先发生在侵彻接触区域面板的变形，发生拉伸失效，产生花瓣撕裂破坏，而泡沫芯层因拉伸和剪切联合作用发生压溃破坏。

图6为半球形弹体侵彻夹层板过程中的速度历程曲线。速度变化主要经历了 3 个阶段：第 1 阶段，弹体接触上面板开始直至穿透上面板，弹体速度急剧下降；第 2 阶段，在该阶段弹体开始接触泡沫铝芯层直至完全穿透，在该阶段时间的长短与泡沫铝力学性能和芯层厚度密切相关；第 3 阶段，弹体接触下面板开始直至穿透下面板。从分析可以看出，在上述 3 个阶段中，第 1 阶段夹层板吸能最多，第 3 阶段次之，第2 阶段最少；同时弹体贯穿下面板所需要的时间相对于上面板的时间要长，这是因为侵彻芯层和下面板时其弹体的速度较前者小。

图 6 半球形弹体速度随时间历程曲线Fig. 6 Hemispherical-nosed projectile velocity history curve

2.2.2 夹层板塑性变形分析

图7给出了夹层板上、下面板和泡沫芯层的变形曲线对比。从图中可以看出距弹体撞击区域越近，夹层板各部分的变形程度也就越大。同时可以看出，在离弹体侵彻区域较远时下面板变形最大，泡沫芯层次之，上面板的变形最小；在弹体侵彻区域附近时下面板变形最大，上面板次之，芯层的变形最小。这是由于夹层板上面板、泡沫芯层和下面板之间相互接触，板间各部分存在的相互作用力不同的缘故。

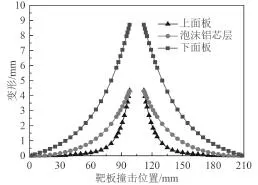
图 7 半球形弹体撞击泡沫铝夹层板变形曲线对比Fig. 7 Comparison of deformation profiles of aluminum foam sandwich plate under hemispherical-nosed projectiles

3 芯层参数影响分析

3.1 芯层厚度对其抗侵彻性能的影响

泡沫铝芯层的材料特性和厚度对其抗侵彻性能具有明显影响。因此，本节讨论芯层厚度对结构抗侵彻性能的影响，选取 4 种不同厚度的芯层，分别为10 mm，20 mm，30 mm 和 40 mm，芯材密度为 276 kg/m3，同时选择 2 种 0.6 mm 和 0.8 mm 厚度的面板进行仿真分析。

3.1.1 剩余速度分析

图8给出了半球形弹体侵彻不同芯层厚度的泡沫铝夹层板的冲击速度与剩余速度曲线关系。从图可知：芯层厚度对夹层板抗侵彻性能的影响与弹体冲击速度有关，在弹道极限速度附近，芯层厚度对夹层板

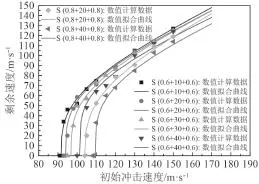
图 8 不同厚度芯层泡沫铝夹层板初始速度与剩余速度关系Fig. 8 Residual velocity of aluminum foam sandwich plates versus initial velocity for various foam core thicknesses

抗侵彻性能影响较大，随着弹体速度增加到一定程度后，芯层厚度对剩余速度影响逐渐减小。

3.1.2 弹道极限速度分析

图9为夹层板在半球形弹体冲击下，弹道极限与芯层厚度的关系，其中夹层板上、下面板厚度均为0.6 mm。从图9可以看出，泡沫铝芯层厚度越大，其相应的弹道极限速度也越高，且弹道极限速度与泡沫芯层厚度为准线性关系。

图 9 弹道极限与夹层板芯层厚度的线性关系Fig. 9 Linear relationship of between foam core thickness and ballistic limit velocity

3.1.3 吸能性能分析

图10给出了半球形弹体侵彻不同芯层厚度的泡沫铝夹层板的冲击速度与能量吸收曲线关系。从图中可知：1）相同冲击条件下，夹层板的吸能能力随着芯层厚度的增大而增大；2）随着弹体冲击速度的提高，夹层板的吸能能力均呈现先减小后增大的趋势；3）在弹道极限速度附近，面板厚度对夹层板抗侵彻性能的影响大于芯层厚度的影响，而随着初始冲击速度的增大，面板厚度的影响逐渐减弱。

3.2 芯材密度对其抗侵彻性能的影响

选取 4 种不同密度：197 kg/m3，276 kg/m3，497 kg/m3和541 kg/m3的泡沫铝芯材，讨论其对夹层板抗侵彻性能的影响，同时选择 2 种 0.6 mm 和 0.8 mm 厚度的面板进行仿真分析。

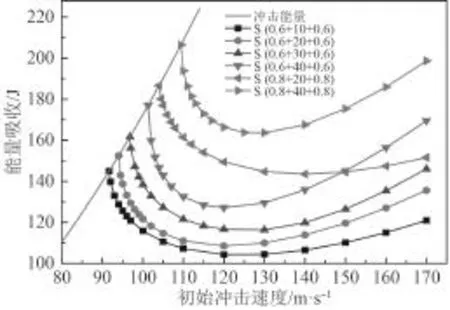
图 10 不同芯层厚度泡沫铝夹层板初始速度与能量吸收关系Fig. 10 Energy absorption of aluminum foam sandwich plates versus initial velocity for various foam core thicknesses

3.2.1 剩余速度分析

图11给出了半球形弹体侵彻不同芯材密度的泡沫铝夹层板的冲击速度与剩余速度曲线关系。从图可知：芯材密度对夹层板抗侵彻性能的影响与弹体冲击速度有关，在弹道极限速度附近，芯材密度对夹层板抗侵彻性能影响较大，随着弹体速度增加到一定程度后，芯材密度对剩余速度影响逐渐减小。

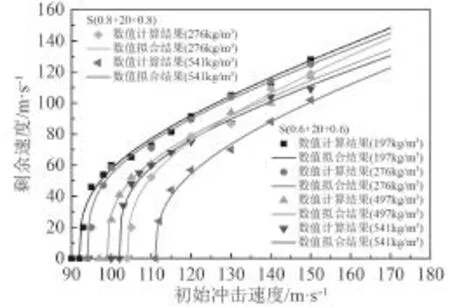
图 11 不同密度泡沫铝芯层夹层板初始速度与剩余速度关系Fig. 11 Residual velocity of aluminum foam sandwich platesversus initial velocity for various foam core densities

3.2.2 弹道极限速度分析

图12为夹层板在半球形弹体冲击下，弹道极限速度与芯材密度的关系，其中夹层板上、下面板厚度均为0.6 mm。从图11可以看出，泡沫芯材密度越大，其相应的弹道极限速度也越高，且弹道极限速度与芯材密度为准线性关系。

3.2.3 吸能性能分析

图13给出了半球形弹体侵彻不同芯材密度的泡沫铝夹层板的冲击速度与能量吸收曲线关系。可知：1）相同冲击条件下，夹层板的吸能能力随着芯材密度的增大而增大；2）随着弹体冲击速度的提高，夹层板的吸能能力均呈现先减小后增大的趋势；3）在弹道极限速度附近，面板厚度对夹层板抗侵彻性能的影响大于芯材密度的影响，而随着初始冲击速度的增大，面板厚度的影响逐渐减弱。

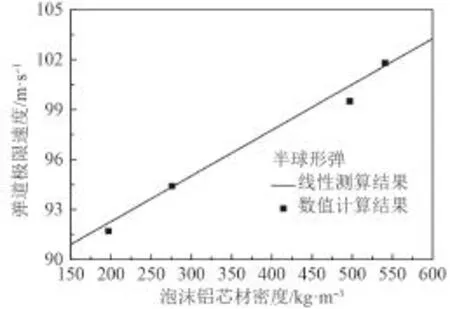
图 12 弹道极限与夹层板芯材密度的线性关系Fig. 12 Linear relationship of between core density and ballistic limit velocity

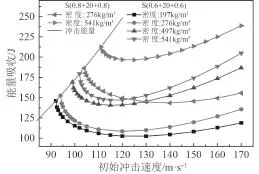
图 13 不同冲击速度下不同芯材密度泡沫铝夹层板的吸能情况Fig. 13 Energy absorption of aluminum foam sandwich plates versus initial velocity for various core density

4 结 语

本文通过实验对泡沫铝材料在准静态条件下的压缩性能进行研究，基于实验结果参数，通过数值方法研究了面板为Q235钢、芯层为泡沫铝的夹层板在半球形弹体冲击下的动态响应及抗侵彻性能。得出以下结论：

1）闭孔泡沫铝压缩应力-应变曲线具有泡沫材料典型的三阶段特征，即线弹性阶段、屈服平台阶段和压实阶段。泡沫铝材料的弹性模量随着密度的增大而增大。基于实验结果得到的压缩本构模型与参数能准确描述泡沫铝材料的力学性能。

2）在半球形弹体的侵彻下，夹层板主要发生较大的结构变形，面板主要发生拉伸失效，产生花瓣撕裂破坏，泡沫芯层因拉伸和剪切联合作用而发生破坏。

3）夹层板各部分的变形程度有所差异。距弹体撞击区域越近，夹层板各部分的变形程度也就越大。在离弹体侵彻区域较远时，下面板塑性变形最大，泡沫芯层次之，上面板最小；在弹体侵彻区域附近时，下面板塑性变形最大，上面板次之，芯层最小。

4）随着弹体冲击速度的提高，夹层板的吸能能力均呈现先减小后增大的趋势。

5）在弹道极限速度附近，面板厚度对夹层板抗侵彻性能的影响大于芯层厚度或芯材密度的影响，而随着初始冲击速度的增大，面板厚度的影响逐渐减弱。

6）弹道极限速度随着泡沫铝夹层板芯层厚度或芯材密度的增大而增大，且弹道极限速度分别与芯层厚度或芯材密度近似线性。