优美的不等式“ln（x+1）≤x”

安徽合肥一中 张旭升

近年各地的模拟试题及高考试题中，经常会出现lnx的身影，尤其在函数式中含有lnx，证明不等式及恒成立问题，直接求导来解题还是比较麻烦的，利用lnx的不等式进行放缩，会避免繁杂的求导运算，小巧别致。

不等式：若x≥0，则ln（x+1）≤x。

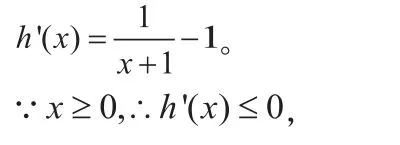
∵h(x)在[0，+∞）上递减，

∴h(x)≤h(0)=0。∴ln（x+1）≤x。

【例题1】已知函数f(x)=xlnx。（1）若函数g(x) =f(x) +x2+ax+2有零点,求实数a的最大值；（2）若恒成立,求实数k的取值范围。

分析：对于恒成立问题，我们的常用方法是分离参数k。本题容易分离但是函数的最小值不易求，故采用下面的解法。

∴h(x)在(0,1)上递增，在(1,+∞)上递减，

∴h(x)max=h(1)=0。∴k=0符合。

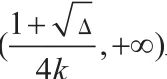
∴x＞0使h′(x)＜0，∴k＜0符合。

综上：k≤0。

解法二：利用lnx的不等式另解：

由于ln（x+1）≤x，故lnx≤x-1(x≥-1)。

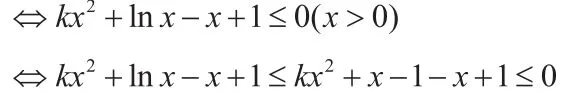
即：kx2≤0。又x＞0，故k≤0。

可见，利用lnx的不等式将在很大程度上减少分类讨论。

【例题2】设数列{an}的前n项和为Sn，且对任意的n∈N＊，都有（1）求a1，a2的值；（2）求数列{an}的通项公式an；（3）证明：

解：（1）略。

（2）过程略，an=n。

（3）证法一：

当k≥2时，通项

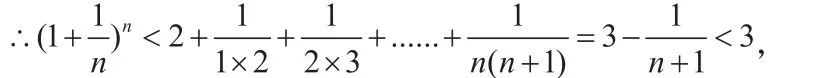
所以，不等式成立。

要证上式成立，

由lnx的不等式知显然成立，故得证。

近年高考试题中，若利用lnx的不等式解决不等式及恒成立问题也会起到事半功倍的效果。

【例题3】（山东卷理科第21题）已知函数

解：（1）由已知得函数f(x)的定义域为{x|x＞1}，

当 x ∈（1，x1）时，f′(x)＜ 0，f(x)单调递减；

当x∈（x1，+∞）时，f′(x)＞0，f(x)单调递增。

当a≤0时，f′(x)＜0恒成立，所以f(x)无极值。

当n为偶数时，

所以当x∈[2，+∞）时，g(x)单调递增，又g(2)=0，

所以f(x)≤x-1成立。

当n为奇数时，

所以当x∈[2，+∞）时，h(x)=x-1-ln(x-1)单调递增，

又h(2)=1＞0，所以当x≥2时，恒有h(x)＞0，即ln(x-1)＜x-1成立。

综上所述，结论成立。

故只需证明1+ln(x-1)≤x-1，

即证ln(x-1)≤x-2，

令 t=x-2(t≥ 0)，

即证ln(t-1)≤t，

由lnx的不等式知显然成立。

可见在本题中，采用ln(x-1)≤x-2解题，会使得解题思路很清晰明了。

总之，利用lnx的不等式，把lnx放缩变形成多项式，不仅会避免繁杂的求导运算，而且解法简明，新颖别致，仅供大家参考。