厘清经济学原理灵活构造递延年金现值的计算方法
彭 滔
(海南外国语职业学院,海南 文昌 570200)
年金是一个重要的经济学、财务学上的概念。年金是一组现金流,它通常具有两个特性:等额、定期。等额表示每次支付的金额必须一样多,不能每期的数量不一致,有时多有时少,流量不均匀;定期要求支付的时间每次都必须一致,要么都在期初,要么都在期末,不能这期在期初,下期在期末。满足这两个条件的现金流才是本文讨论的对象。既然是一组现金流,那么就可以计算它的现值和终值。
下面我们使用一个具体实例,使用EXCEL工具,来分析讲解,如何计算递延年金的现值,它有哪些实际上的应用价值,本文提出了3中不同的计算思路,用EXCEL得到了相同的计算结果,做到了相互应证。
场景:银行存款利率3%,复利计息。
A先生的小孩正在上高一年级,他希望3年后,小孩开始读大学,在上大学的4年时间中,每年都能够从银行中取出30000元,作为小孩的学费和生活费。
A先生需要在当前一次性存入多少钱?
思路1:现金流贴现法
本题中的现金流用数组来表示:前3年,每年不发生现金流,用0表示;后4年,每年从银行提取30000元,用4个连续的30000表示。

对于C列:C3中的表达式为=B3/(1+$B$1)^A3下拉到C9
C10中的表达式=SUM(C3:C9)

附表1 现金流贴现法
为了在未来产生一组这样的现金流,[0,0,0,30000,30000,30000,30000]
现在必须在银行中存入102050.1元。
思路2:两组现金流PV差值法
符号约定:A先生将款项存入银行,现金从A先生手上流出,使用负号;A先生从银行提取现金,现金流入A先生手上,使用正号。
PV函数的使用方法:PV(rate,nper,pmt,fv,type)
各个参数的含义
Rate:利率 nper:期限 pmt:期间的支付 fv:未来值 type:类型(期初支付还是期末支付)
第一组现金流 [30000,30000,30000,30000,30000,30000,30000]
第二组现金流 [30000,30000,30000]
结合附表2,第一组现金流的现值 D2=PV(B5,B3,B2)
第二组现金流的现值 D3=PV(B5,B4,B2)
计算结果=差值=D2-D3
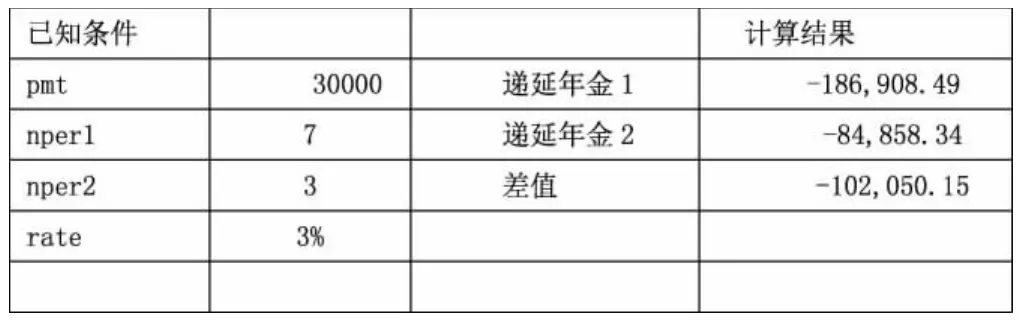
附表2 两组现金流PV差值法
思路3:PV再贴现
后4年的PV计算出来后再贴现到当前
符号约定同思路3.


附表3 PV再贴现
从上面的分析来看,思路1最直接,最易于接收,并且不要求等量现金流这个前提条件;思路2有点类似几何题中增加一条辅助线的做法,将两组现金流的PV值的差,等效于我们需要计算的结果;思路3分成两步,步步逼近,也是一个好办法。
从本例可以看出,全面了解经济学、财务学上的概念后,可以更加灵活的构建不同的计算方法,从易于理解的方面来说,我推荐思路1计算本例的递延年金现值。

