地球同步轨道卫星结构爆炸解体碎片的轨道仿真

周宵灯，崔村燕，赵蓓蕾，詹 翔，王 岩

(1. 航天工程大学 研究生管理大队,北京 101416； 2. 航天工程大学 宇航技术系，北京 101416)

0 引言

当前，空间碎片已成为全球共同面临的空间环境污染问题。为加强空间碎片管理，美国航空航天局(NASA)依据空间监视网(SSN)的观测数据和轨道测量结果对碎片进行编目，并形成与之配套的“两行轨道根数”(TLE)数据。但美国SSN所用的雷达和望远镜的观测能力有限，在低轨(LEO)范围内可观测和编目的空间目标的最小尺寸约为10 cm，在地球静止轨道(GEO)上约为1 m。此外，尽管国外已建立了EVOLVE、ORDEM、MASTER[1-5]等多种空间碎片环境模型，但建模的数据主要源于SSN编目、雷达探测、望远镜观测、航天器回收表面分析等10类探测数据，缺乏cm级碎片的直接探测数据，只能通过μm级(由长期暴轨装置LDEF获得)和cm级以上碎片数据插值获得[6]。国内尚无公开的具有国际影响力的空间碎片环境模型，相关研究基本围绕碎片探测、空间目标碰撞、轨道优化等方面展开[7-10]。

卫星爆炸解体产生的碎片一直是尺寸从几毫米至几分米的空间碎片的主要来源，这一尺寸范围内的碎片包括直径为1～10 cm的特别危险的碎片，现有的在轨技术无法对其进行防御，监视网也无法跟踪。因此，开展对卫星爆炸碎片轨道的研究，快速掌握爆炸碎片轨道分布特性，特别是难以探测的cm级碎片的运行轨迹极具现实意义。

本文基于ANSYS/AUTODYN软件对模拟卫星结构进行爆炸数值仿真，将仿真得到的碎片参数作为初始数据，利用MATLAB将大量数据导入STK的SGP4模型中，得到所有碎片的轨道信息，并从碎片的轨道分布、速度增量、轨道演化、寿命估计等方面展开分析，以期为快速捕获卫星爆炸碎片，及时规避航天器碰撞提供参考。

1 卫星爆炸仿真

真实卫星形式多样，结构复杂，爆炸解体过程和碎片分布特性受诸多因素影响。为简化分析计算过程，本文以在轨柱形卫星为研究对象。根据能量守恒定律，将卫星推进剂等效为TNT炸药，推进剂液态肼爆炸的TNT当量系数Y为0.93[11]，转化后的TNT炸药质量为164 g；根据结构强度等效方法将卫星壳体等效为厚度为3 mm，壳体尺寸Φ为100 mm×150 mm，壳体材料为铝合金的薄壳圆柱；选取位于圆柱中心线上距离端面10 mm处的卫星推进剂的质心为炸点。

AUTODYN是一个显式有限元分析程序，由ANSYS子公司研发，在国际军工市场占比超过80%，为爆炸的应用案例求解提供了更高的精确度[12]。本文采用AUTODYN 15.0进行数值仿真，数值模型由TNT炸药和铝合金壳体2部分组成，在对爆炸碎片形成过程进行模拟时采用SPH算法，选择粒子间距为1 mm。

柱形卫星因内部推进剂爆炸而膨胀与破碎的过程如图1所示。卫星爆炸仿真最终生成了533块质量大于10 mg的碎片，其中质量小于100 mg的碎片占大部分，具体分布如图2所示。

图1 卫星壳体膨胀与破碎过程Fig.1 Expansion and fragmentation of satellite shell

图2 碎片质量分布Fig.2 Mass distribution of debris

2 碎片轨道仿真

SGP4模型是在美国广泛使用的标准外推模型，与TLE一起使用。它考虑了由地球非球形引起的长期和周期变化、日月引力、引力场共振效应，但并未充分考虑大气阻力、太阳风等空间环境因素，只是简单地使用一个阻力模型来计算产生的轨道衰变，导致计算结果精度不高，在进行轨道演化和寿命分析时，只能用作大致参考。SGP4模型为解析模型，优点是计算速度快，本文选择该模型的目的是在第一时间获得爆炸碎片的轨道概况。SGP4模型是一种高效率的通用算法，但只有当输入为TLE轨道参数时，计算结果才有效。TLE文件由美国战略空间司令部开发，是以SGP4模型对空间目标进行轨道预报的数据文件格式，文献[13]对其格式进行了详细说明。

本文以地球同步轨道卫星的爆炸仿真数据作为爆炸碎片的初始参数，其中包括碎片位置、速度等关键信息。AUTODYN软件可输出碎片在x、y、z方向上的速度值，通过与地面爆炸破片速度计算公式(即Gurney公式)进行对比可验证仿真结果的准确性。相比于碎片与地球之间的距离，爆炸能量使碎片产生的初始位移可忽略不计。通过假设碎片的初始位置不变，确定碎片的直角坐标，再通过公式将坐标转化为轨道六要素，得到碎片的初始TLE轨道参数。整个分析过程如图3所示。首先利用拉格朗日法对某简化柱形卫星进行爆炸仿真，通过后处理得到卫星爆炸后碎片的初始位置和速度参数，然后通过与经验公式作对比验证爆炸仿真的准确性，如果仿真结果与理论计算相一致，则继续下一步，否则重新设置参数进行卫星爆炸仿真。通过MATLAB编程，将爆炸碎片初始位置和速度参数转化为TLE数据文件格式，将其作为输入导入SGP4模型，得到该卫星爆炸后碎片的初始轨道。

图3 卫星爆炸碎片分析流程Fig.3 Analysis process of satellite explosion debris

2.1 爆炸碎片轨道分布

将TLE文件导入到SGP4模型后得到的碎片轨道分布情况如图4所示。其中：红色线条为目前正在运行的GPS导航卫星的轨道，黑色线条为爆炸碎片的运行轨道。在卫星和碎片运动轨道参数已知的条件下，借助STK软件，就可实现实时的轨道预警。在可能发生碰撞的位置，卫星采取轨道机动的方式，避免与碎片发生碰撞。

图4 碎片轨道分布图Fig.4 Debris orbit distribution

为进一步分析爆炸碎片的轨道分布情况，选取爆炸碎片中的4个典型单元进行模拟研究。因爆炸能量使碎片产生的初始位移可忽略不计，故碎片的位置参数可选用卫星发生爆炸时的位置(42 154.8，-982.731，0)，单位为km。卫星和各碎片单元在该位置的速度参数见表1。

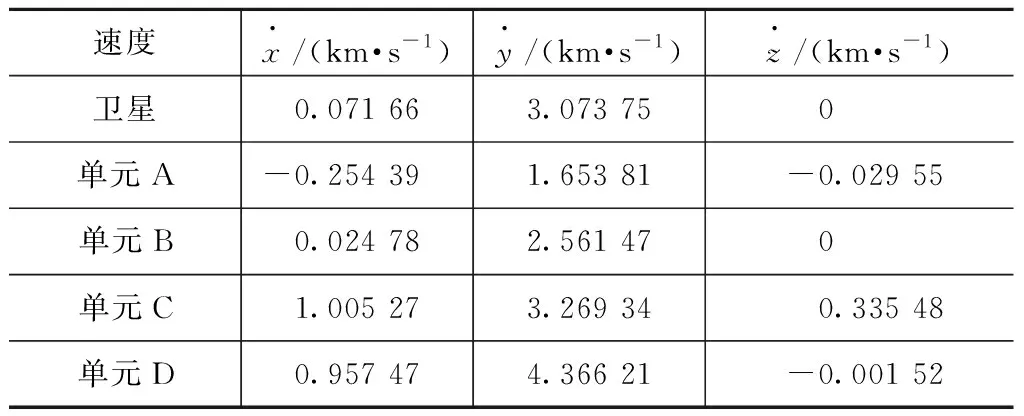
表1 卫星和各单元速度参数

将经转化后的数据代入模型，得到卫星与各单元的运行轨道，如图5所示。结合轨道仿真结果和力学分析，可将爆炸产生的碎片运行轨迹分为4种类型：当碎片速度小于卫星运行速度且小于某一临界值V1时，碎片就会像A单元一样落入大气层，不会变成太空垃圾污染空间环境；当碎片速度小于卫星速度但大于临界值V1时，碎片的运行轨迹如B单元，碎片绕着地球做椭圆运动，但运行范围小于原来卫星的范围；当碎片速度大于卫星运行速度且大于某一临界值V2时，碎片就会像D单元一样脱离地球引力飞向更远的地方；当碎片速度大于卫星运行速度且小于某一临界值V2时，碎片的运行轨迹如C单元，碎片绕着地球做椭圆运动，但运行范围大于原来卫星的范围。

图5 卫星与各单元运行轨道Fig.5 Orbits of satellite and each unit

通过活力公式可求得临界值V1和V2的理论值，将其与仿真结果进行对比，对比结果见表2。

由表可见，数值仿真与经验估算的结果非常接近，其相对误差在允许范围之内。数值仿真结果之所以略大于公式推导结果，是因为在公式推导中，未考虑轨道摄动力的影响。

表2 临界值V1、V2数值仿真与公式推导结果对照

2.2 爆炸碎片速度增量分析

卫星发生爆炸时，爆炸冲量使碎片获得的速度增量为Δv，碎片速度的改变引起了轨道根数的变化。爆炸碎片的轨道根数变化与速度增量的关系为

式中：Δvx、Δvy、Δvz为轨道坐标系O-xyz各轴上的速度增量；Δa、Δe、Δω、ΔΩ、Δi、ΔM为轨道根数的变化，其中，a为半长轴，e为偏心率，ω为近地点幅角，Ω为升交点赤经，i为轨道倾角，M为平近地点角；μ=3.986 005×1014m3/s2，为地球引力常数；r=(x2+y2+z2)1/2，为卫星到地心的距离；u=1/r；p为近地点。由上式可知，爆炸碎片的速度增量Δvx和Δvy决定了平近地点角、偏心率和半长轴的变化，而Δvz则决定了升交点赤经和轨道倾角的变化。

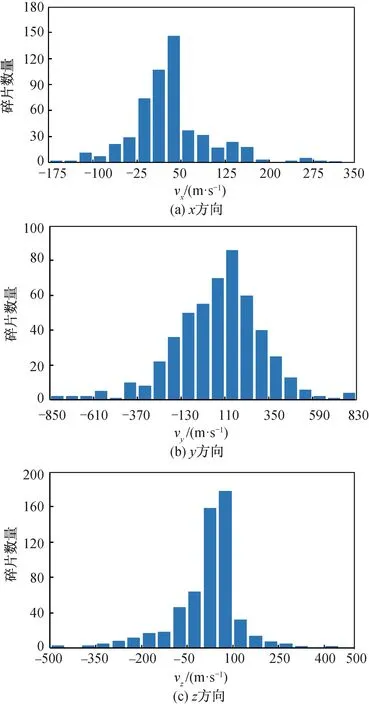
图6 爆炸碎片在x，y，z三个方向上的速度增量频次分布Fig.6 Velocity increment frequency distribution of explosion debris in three directions of x, y and z

以卫星爆炸仿真得到的碎片参数为依据，分析爆炸碎片在x、y、z三个方向上的速度增量，结果如图6所示。由图可知，在x方向上的速度增量分布范围为-200～300 m/s，其中在-25～25 m/s之间碎片分布最为集中，爆炸碎片在x方向上的速度增量均值为7.9 m/s，y方向上的速度增量均值为9.2 m/s，z方向上的速度增量均值为-9.6 m/s。

2.3 爆炸碎片轨道演化

轨道演化是一个动态过程，想要清楚地看到轨道的变化情况，需要一个较大的时间差。图7是将STK中的场景时长从原来的1个月，增加到3年后的B单元的轨道情况。由图可见，B单元的运行轨迹并非是一条线，而是一个区域，这是因为随着运行时间的增加，原来的计算模型的误差将会不断积累，轨道会发生很大变化。

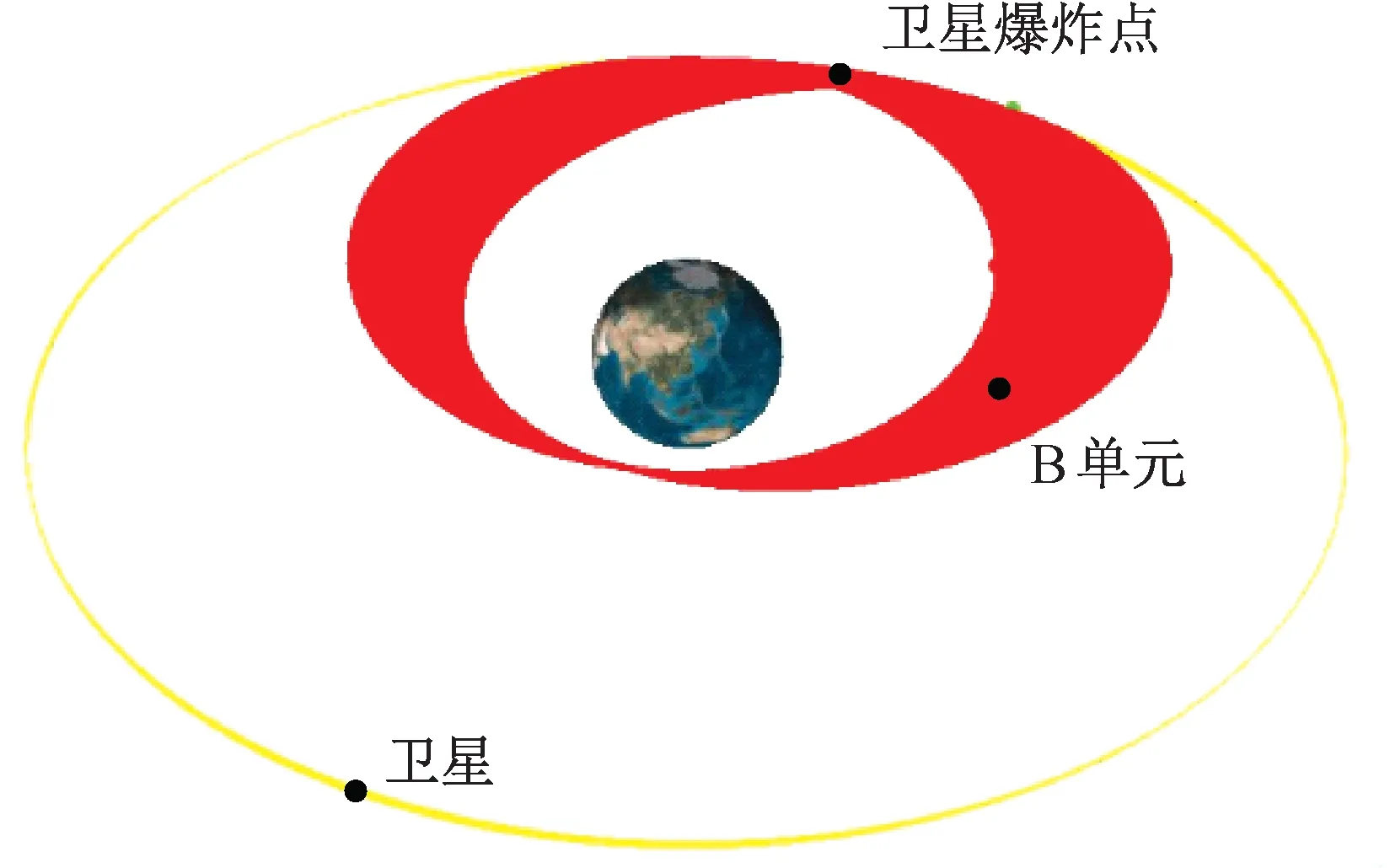
图7 B单元运行轨道Fig.7 Operating orbit of unit B

3 结束语

本文利用MATLAB将AUTODYN爆炸仿真软件与航天分析软件STK联系到一起。仿真结果表明：SGP4模型运算速度快，满足大量爆炸碎片的轨道仿真的要求。通过应用轨道动力学和天体力学的相关知识分析碎片受力情况，可以发现，摄动分析的精度严重受到摄动力模型的影响，而不同仿真模型采用的内部摄动力模型也各不相同。因此，从理论与仿真两方面进行分析验证极为必要。本文对爆炸碎片的运行轨道进行了分类。在具体分析碎片运行对航天器的危害时，可去除落入大气层和飞入僵尸轨道的碎片，以减少任务量，提高计算效率；可对碎片进行威胁评估、跟踪和编目。

如何快速确定与预报卫星在轨爆炸解体产生的大量空间碎片，以提供及时的空间碰撞预警是目前空间态势感知的一个重要研究方向。本文提出的方法受SGP4模型限制，对摄动力模型进行了简化，未充分考虑高低温、太阳风等空间环境的影响，导致仿真结果精度不够。后续研究可从模型本身出发，进一步考虑空间环境因素，应用更精确的大气密度模型，利用地面观测数据对分析轨道进行修正，以提高计算精度。