基于相关峰细化时延估计的舱内服务机器人发话人定位研究

王啸臻，王兆魁，张育林,

(1.国防科技大学 空天科学学院，湖南 长沙 410073； 2.清华大学 航天航空学院，北京 100084)

0 引言

当前空间站的稳定运营主要依赖于航天员的长期在轨工作。航天员需要独立完成飞船操控、在轨科学实验操作、科学演示等多项任务，在轨工作效能有限。随着机器人技术的快速发展，利用机器人辅助完成在轨任务成为可能。国际上已先后提出多个舱内辅助机器人项目，如PSA[1]、Astrobee[2]，以及曾在国际空间站服役的Smart Spheres[3]和Int-Ball等。这些机器人多采用遥控方式运行，其自主运行、人机智能交互能力有限，需要航天员在轨照料。为发展更自主的舱内服务机器人，提升机器人的任务辅助能力，需要解决机器人对航天员的信息感知问题。惯性与视觉导航主要用于获取舱内的相对位置和姿态，而舱内机器人无法有效实时地获取航天员的相对位置。利用麦克风阵列进行声源定位，感知航天员的语音信息，可有效区分航天员与环境，实时获取航天员角度位置关系，这一方法计算速度快，结构简单。

目前使用麦克风阵列进行声源定位的方法一般可分为3类：基于高分辨率谱估计、基于可控功率响应和基于时延估计。而机器人声源定位系统一般要求麦克风阵列数量少且易搭载，机器人运动特性则要求定位方法高效迅速且具备一定的抗混响和抗噪声能力[4]。由于基于时延估计的声源定位方法计算复杂度低，实时性高，且硬件成本较低，因此在机器人系统中得到了广泛应用。

基于时延估计的定位方法是一种双步定位方法，它首先估计声源到达不同麦克风的时间差，再利用得到的时延结合麦克风阵列结构，确定声源的位置[5]。自1976年以来相关学者提出了许多时延估计的算法，如基于声学传递函数比的算法[6]、基于基音加权的算法[7]、基于自适应特征值分解的算法[8]、基于广义互相关函数的算法[9]等。广义互相关函数法由于其计算速度快且符合实时解算要求，因此应用最广泛，它通过计算两路信号的互相关函数求取峰值，相关函数峰值对应的时间就是两路信号的时延差。这类方法原理简单，但受噪声和时域采样频率的限制，所以时延估计精度不高。

为提高时延估计精度，针对广义互相关时延估计方法使用快速傅里叶变换(FFT)会在频域上产生栅栏效应，从而影响时延估计精度的问题，提出了基于相关峰精确插值(FICP)的空间六元阵列发话人定位方法。该方法基于机器人球形结构设计，利用谱减法和二次相关降低噪声干扰，通过对声音信号进行频谱细化提高相关函数的时间分辨率，能有效改善FFT带来的栅栏效应，提高时延估计及定位精度。改进算法既继承了相关峰插值算法的优点，又增强了语音处理的抗噪声能力。本文对传统广义互相关算法和改进算法在时延估计准确性方面进行了比较分析，实验结果表明：改进算法可有效改善发话人定位性能。

1 基于球形结构的空间六元阵列定位原理

考虑到舱内服务机器人为球形结构设计(直径D=230 mm)，因此系统中的麦克风阵列结构采用空间六元阵。空间六元阵可进行全空域声源定位，相比平面四元阵在保证分维特性的同时还拥有更优的定位精度[10]。舱内服务机器人结构如图1所示。

图1 舱内服务机器人结构Fig.1 Layout of assistant robots

在直角坐标系下对空间六元麦克风阵列进行描述，如图2所示。6个阵元的坐标分别为M1(d/2，0，0)、M2(0，d/2，0)、M3(-d/2，0，0)、M4(0，-d/2，0)、M5(0，0，d/2)、M6(0，0，-d/2)，其中d为阵列孔径；r为目标(声源)S(x，y，z)到阵列中心(坐标原点)的距离；φ为目标方位角；θ为目标俯仰角；C为空气中声音传播速率。假设目标为点声源，到达各阵元的传播时间为τi(i=1,2,…,6)，则目标到各阵元的距离为ri=C·τi(i=1,2,…,6)。若到达两阵元的时延差为τij，则声源到M1和M3的距离差d1=C·τ31，到M2和M4的距离差d2=C·τ42，到M6和M5的距离差d3=C·τ65。

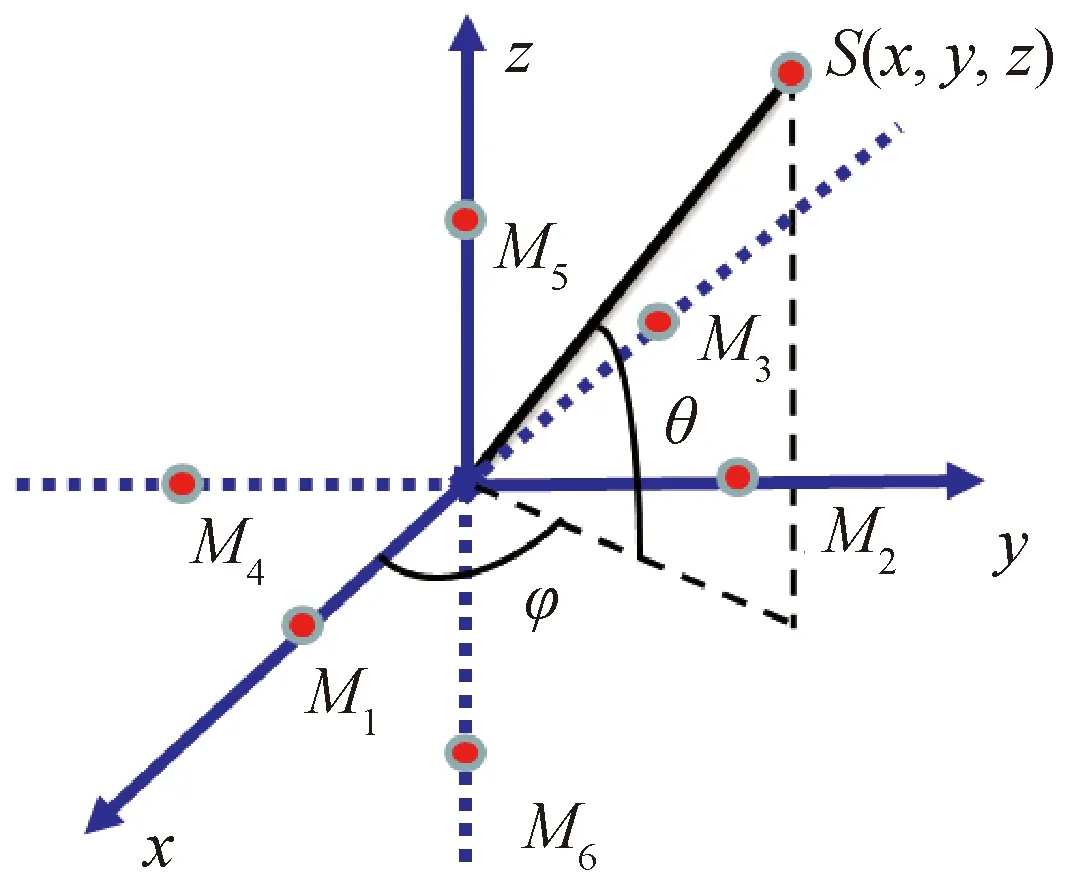
图2 空间六元阵列结构Fig.2 Schematic diagram of six-element cone-shaped microphone array

由麦克风阵列和目标的几何位置关系可联立方程组

(1)

由直角坐标与球坐标的转换关系可得目标方位信息r、φ、θ。因r，ri≫dj，故可得

(2)

(3)

对式(2)、(3)进行简化和反三角变换可得方位角φ和俯仰角θ的解算表达式为

(4)

平面四元阵列的方位角和俯仰角的解算表达式[11]为

(5)

根据实际测量经验，一般得到的方位角和俯仰角误差较小，而距离的测量误差较大。考虑到机器人的实际需要，仅得到高精度的角度测量信息即可准确找到人员位置，从而能为视觉导航与人机交互提供辅助，因此本文仅给出角度测量公式。式(5)中测角精度受声速估计误差和阵元安装误差影响。由式(4)可知，空间六元阵测量方位角φ和俯仰角θ仅与时延τij有关，与声速C和阵列孔径d无关，定位精度受时延τij和声速C的估计误差影响。对比平面四元阵，空间六元阵的测角受干扰更小，定位精度更高。由此可见，得到高精度的时延估计值即可求得较准确的角度位置信息。

2 基于相关峰精确插值的改进时延估计算法

2.1 相关峰精确插值算法

为提高相关函数的分辨率，对相关峰进行插值计算，一般采用基于信号内插法的时延估计算法，其估计精度受限于内插倍数，复杂度较高。如果要达到0.01采样间隔估计精度，需要计算100倍插值，不仅计算量大，还会带来新的误差源，因此需要计算相关峰的精确算法。相关峰精确插值算法的基本思想是针对两路长度均为N点的语音信号，计算其互功率密度谱并进行频域补零，构建完整的频谱序列以提高频谱采样率及时域内相关函数分辨率。FICP算法是在线性调频Z变换(MCZT)的基础上，利用互谱的前后两端计算相关函数的峰值波形，并对相关峰进行细化。FICP算法的具体实现过程如下：

R1(k)=

(6)

2) 对R1(k)补零，将互谱拉长至N2(N2>N1)点，得到新的互谱

R2(k)=

(7)

3) 对R2(k)进行IMCZT逆变换得到相关函数R(n)，由此可突破时域采样率限制，提高相关函数分辨率，其分辨率可提高N2/N1倍。因阵列信号的时延估计值在有限范围内，故仅计算相关函数主峰左右各N点，组成长度为2N的新相关函数，降低运算量。

对于n=0,1,…,N-1的时域范围，相关函数为

(8)

对于n=N2-N,N2-N+1,…,N2-1的时域范围，取n=N2-N+n1,对应n1=0,1,…,N-1的相关函数为

Rn2(N2-N+n1)=

(9)

由Rn1(n)和Rn2(n)组成的相关函数为

Rn(n)=

(10)

经过复杂公式推导[12]，可得化简后的相关函数表达式

(11)

(12)

线性调频Z变换为计算细化频谱的有效方法，计算精度高且运算速度快。DMCZT和DIMCZT分别代表线性调频Z变换及其逆变换，其定义式分别为

(13)

x′(n)=DIMCZT[X(k)]=

(14)

2.2 算法分析与比较

选取一段时长0.3 s的语音信号进行分析，采样频率fs=44 100 Hz，FICP计算参数N1=44 100，N2=500 000。分别用FICP和FFT计算频域频谱，图3选取了包含谱峰的一段频谱图(频率为400～600 Hz)，可以看出用FICP得到的频谱信息比FFT更丰富，谱峰高度也更精确。在谱峰附近，用FFT计算得到的频率依次为470.1、478.2、486.4、502.6、510.7 Hz，用FICP计算得到的频率依次为484、485、486、487、488 Hz，FICP的频谱泄漏更少。通过互功率谱计算能提高时延估计值精度，频谱分辨率从8 Hz提高到1 Hz。用FICP和FFT计算得到的相关函数波形比较如图4所示。可以看出改进算法相当于对峰值附近的一段相关函数进行插值，使峰值附近的相关函数波形更精细，局部分辨率明显提高，时延估计值更逼近真实值，精度更高。

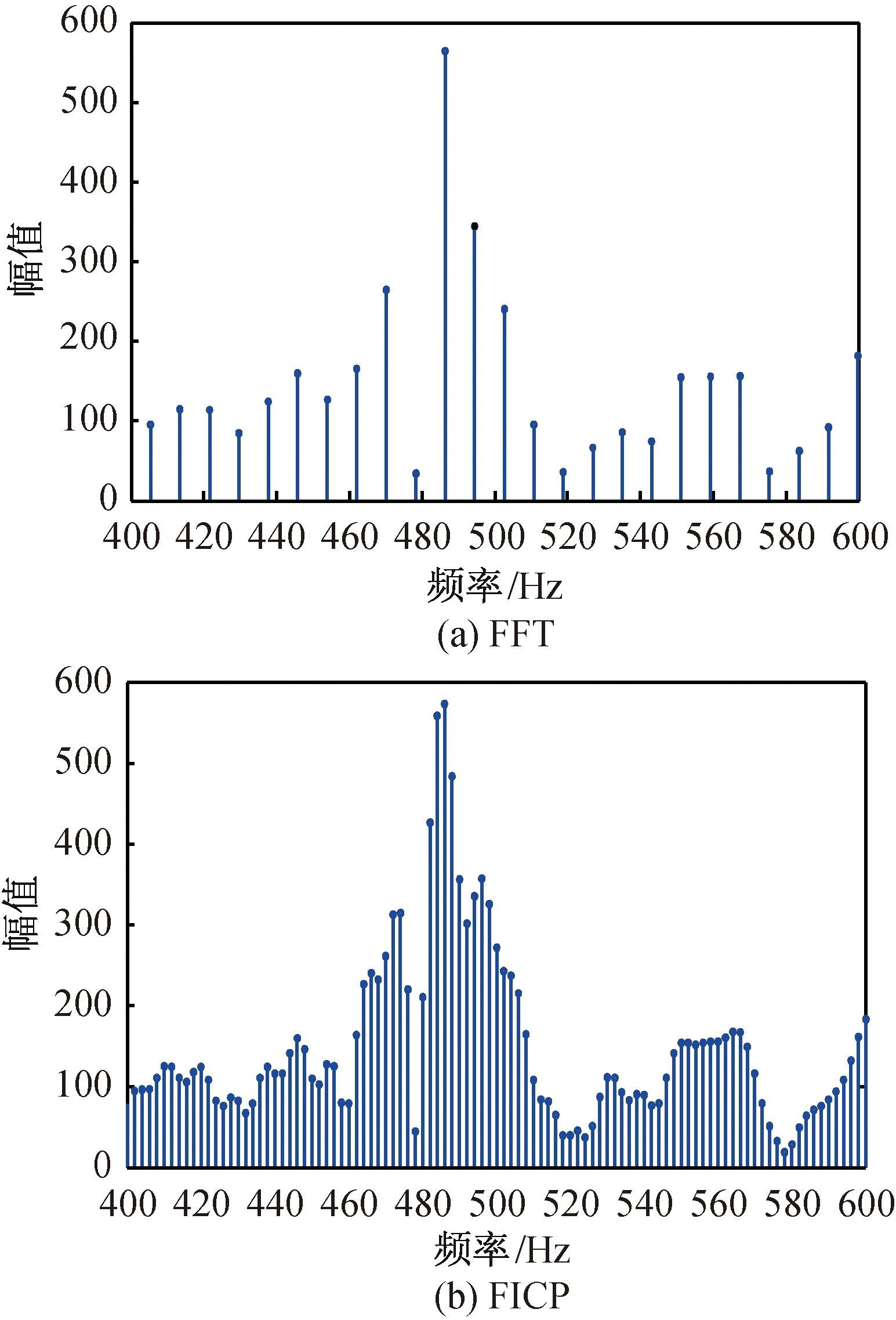
图3 FICP和FFT计算频谱比较Fig.3 Calculated spectra of FICP and FFT algorithms

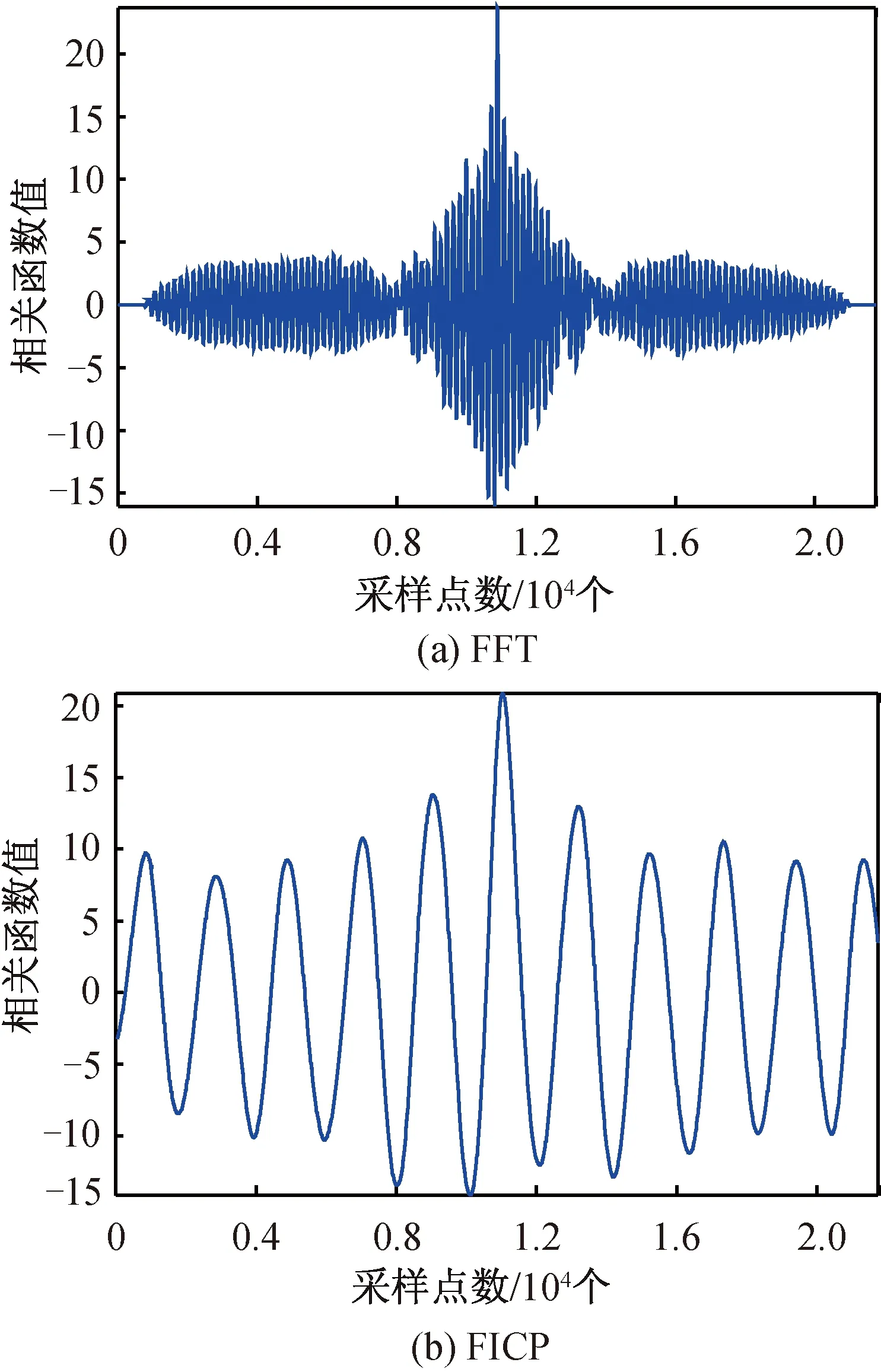
图4 FICP和FFT计算相关函数波形图比较Fig.4 Signal cross-correlation waveforms calculated by FICP and FFT algorithms

2.3 时延估计算法的改进

FICP算法虽然能提高相关函数的分辨率，但并未改进抗噪声性能[13-14]。因此，通过语音信号预处理和二次相关进一步提高算法时延估计的鲁棒性。

首先利用谱减法对语音信号进行降噪处理，设定前导无话段时长估计环境噪声能量，将谱减算法与原信号“作差”得到降噪信号，并利用基于倒谱距离的端点检测筛选有话段，减小互相关函数计算长度，从而提高计算效率。

采用二次相关的目的在于抑制噪声，每进行一次相关计算，都能提高信号的信噪比[15]。对信号1作自相关，对信号1和2作互相关，将信号1的自相关函数和互相关函数作相关计算，进一步削弱噪声影响。时延估计改进算法流程如图5所示。

完整的改进时延估计算法如下：1)利用MCZT取代FFT计算两路预处理后的语音信号1和2的细化频谱来提升频谱精度；2)计算信号1的自功率谱及信号1和2的互功率谱，在此基础上进行二次相关，提高抗噪性能，得到二次互功率密度谱；3)对上述互功率密度谱进行相关峰精确插值，提高二次相关函数的分辨率，通过峰值检测计算得到两路信号的时延差值。

3 算法仿真与实验测试

3.1 FICP算法仿真

实验中分别选取频率fs为20 000、40 000、80 000 Hz的单频正弦模拟信号，预设两接收信号时延差Td=1.7×10-4s，采样点数N=5 000，FICP算法参数N1=10 000，N2=40 000，预设信噪比RSN=8 dB，仿真次数为10次，如图6所示。

图6 10次计算结果比较Fig.6 Comparison of calculation results for ten times

由图6可知，当真实时延值为采样间隔的整数倍时，基于FFT计算的GCC法计算的时延值始终解算为采样间隔的整数倍，而FICP法计算的时延值则可准确求取真值，有

Ts=(1.7±0.02)×10-4s

(15)

式中：Ts为时延估计值。

3.2 真实语音信号处理测试

实验中选取采样频率fs=16 000 Hz，采样点数N=16 347的两路真实语音信号，FICP算法参数N1=16 000，N2=100 000。经过谱减法降噪处理、倒谱距离端点检测筛选有话段后计算时延差。端点检测后得到有话段为58～137帧，计6 321个采样点。语音信号处理如图7所示。

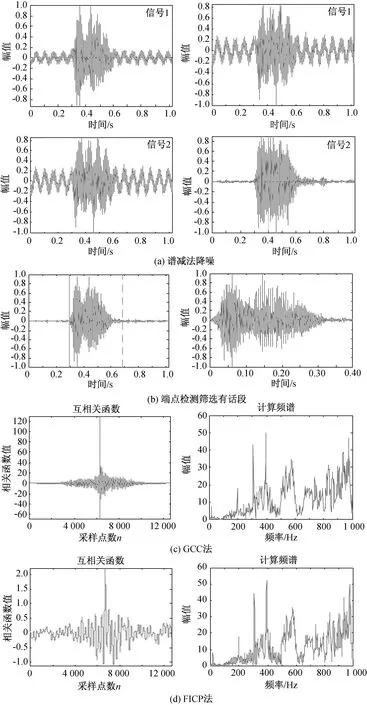
图7 语音信号处理Fig.7 Voice signal processing

从图7可看出，用FICP法得到的计算频谱比GCC法更精细，频谱分辨率得到提升，峰值附近的相关函数波形更精细，局部分辨率明显提高。用GCC法计算的时延估计值为3.75×10-4s，即6个采样时长；用FICP法得到的时延估计值为3.94×10-4s，位于3.75×10-4s(6个采样时长)和4.375×10-4s(7个采样时长)之间。实验结果表明：用FICP法计算的时延值更接近时延差的真实值。

3.3 麦克风阵列定位测试实验

为验证空间六元麦克风阵列的定位效果，进行了静止目标的定位实验，如图8所示。实验条件如下：六元阵列及信号处理模块预设在简易结构的球形模型中，模型直径23 cm，放置在高约20 cm的空心基座上。采用全指向性的PDM数字MEMS麦克风，频率响应20～20 kHz，信号采样频率为16 000 Hz。实际测量中，声源(音响)固定在距离麦克风阵列的一定范围内，通过改变目标声源的相对位置，完成对方位角和俯仰角的实时测量。

图8 空间六元麦克风阵列Fig.8 Six-element cone-shaped microphone array

第1组实验中，声源相对阵列距离分别为50、60、70 cm，保持同一水平高度，方位角φ间隔30°进行音频采集，定位求解结果如图9所示。

图9 方位角测定值Fig.9 Results of azimuth angle measurement

第2组实验中，声源保持同一水平高度，方位角φ设为40°和70°，声源相对距离为40、50、60、70、80、90 cm的6组，采集12次音频，定位求解结果如图10所示。

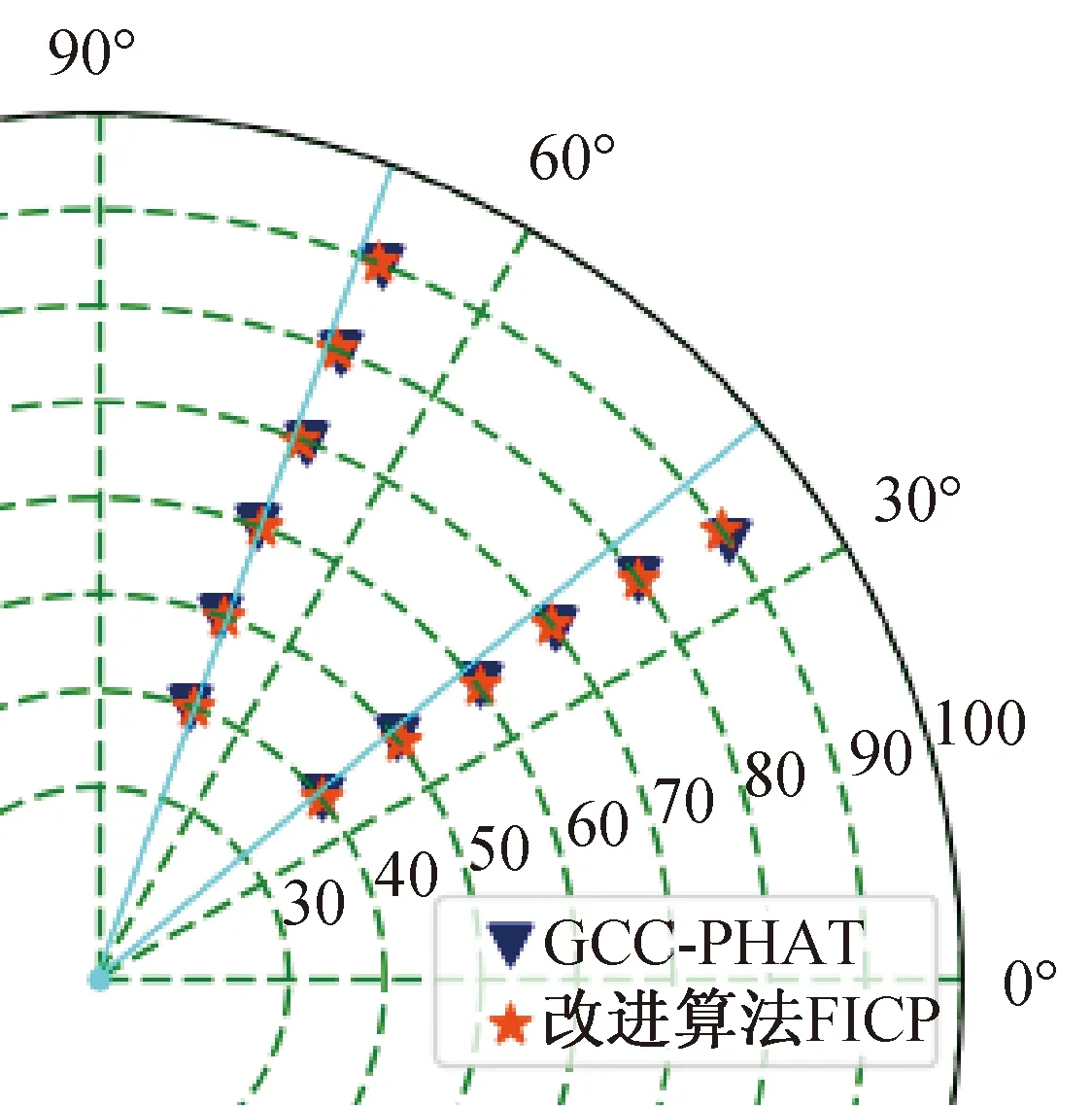
图10 方位角测定值Fig.10 Results of azimuth angle measurement

图9、10对比分析了基于广义互相关与相关峰精确插值这2种声源定位方法的定位结果。发话人定位旨在为机器人视觉导航提供与人员的相对位置关系，由于机器人服务工作在极其有限的舱内空间，优于5°的稳定定位精度即可满足机器人对人员的定位需求。随着相对距离的增大，基于GCC法的方位角测量误差逐渐增大，而基于改进算法的定位准确率则能保持在90%以上。可以看到，基于改进算法的声源定位结果明显优于基于GCC法的声源定位结果。

第3组实验中，声源保持同一方位角和水平距离，方位角φ设为70°，俯仰角θ为70°、80°、90°、100°、110°的5组，采集10次音频，定位求解结果如图11所示。

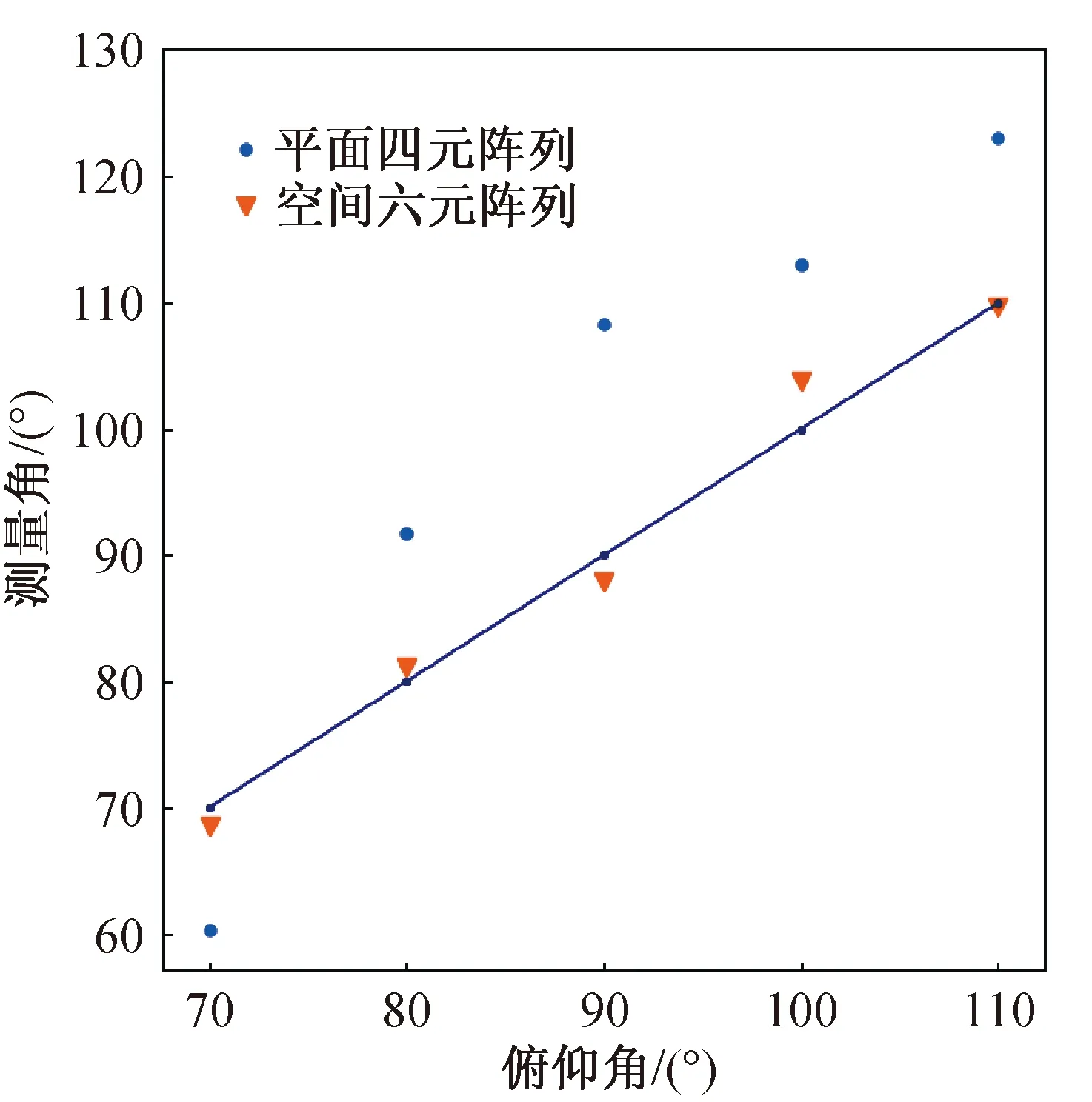
图11 俯仰角测定值Fig.11 Results of pitching angle measurement

图11对比分析了空间六元阵列与平面四元阵列的俯仰角测量结果。可以看到，平面四元阵的俯仰角测量误差很大，而空间六元阵列的俯仰角测量精度相对较高。综上所述，基于改进时延估计算法的空间六元阵列定位方法可有效改善发话人定位性能。

4 结束语

发话人定位是空间站舱内服务机器人实现人员相对位置关系确定及人机交互任务辅助的重要前提。本文提出了基于FICP和二次相关的发话人定位算法，并对算法的流程进行了推导说明。该方法基于机器人球形结构设计，利用信号预处理和二次相关降低噪声干扰，通过对声音信号进行频谱细化以提高相关函数的时间分辨率，能有效改善FFT变换带来的栅栏效应，提高时延估计及发话人定位精度。实验结果表明：相对基于广义互相关的定位方法，基于FICP的空间六元阵列发话人定位方法能得到更高的时延估计精度，从而对发话人进行更准确的定位。未来将围绕发话人定位与视觉导航方法的融合问题展开进一步研究，实现舱内辅助机器人的稳定跟踪。