基于速度滤波的杂波抑制步进频率波形设计研究

董千里，王 飞，宋 柯，陆满君，易 宇

(1. 上海无线电设备研究所，上海 200090； 2. 上海航天技术研究院，上海 201109)

0 引言

杂波是指能产生干扰雷达正常工作的非期望信号的雷达回波[1]。杂波通常具有随机性，即具有独立的幅度和相位。杂波信号强度远大于接收机噪声强度。强杂波会扰乱雷达工作，加大目标检测难度，因此杂波是影响高分辨雷达宽带一维距离像成像质量的重要因素[2-3]。杂波对成像质量的影响主要体现在目标点掩盖和虚假目标点上。目标点掩盖指的是弱目标落入强杂波区，导致目标被淹没，难以发现目标和提取目标信息；虚假目标点指的是个别强杂波强度超过检测门限，在恒虚警检测中杂波被误判为目标点。

机载雷达的探测目标通常是高速运动的物体，比如高速飞行的战斗机、预警机、巡航导弹和其他飞行器，而杂波通常是山坡、树木、植被、建筑等静止物体或鸟群、昆虫、车辆、海浪、云雨等低速运动的物体[4]。目标和杂波在速度上具有很大的差异，利用目标和杂波的速度差异设计波形是改善信杂比的有效途径[5]。

步进频率信号波形具有瞬时带宽小、合成带宽大、距离分辨率高等优点[6]，在雷达成像领域发挥着重要作用。文献[7]提出了一种相位编码步进频率(PCSF)信号，该波形结合相位调制和脉冲频率调制，在保持高距离分辨率的基础上降低了波形的多普勒敏感度。文献[8]提出了一种随机步进频率(RSF)波形，其脉间载频随机步进，通过对比理论和试验数据可以发现，随机步进频率波形能有效降低旁瓣和成像场景中的强噪声，提高抗干扰能力。文献[9]提出了一种调频步进频率信号，该信号脉内调频、脉间步进，兼具脉冲压缩和频率步进的优点，既能实现远距离探测，又可完成高距离分辨。文献[10]提出了一种随机线性调频步进频率信号，将线性调频子脉冲变为随机分布，该波形能以较少的脉冲实现高分辨一维距离像和二维像的重构。文献[11]研究了随机脉冲重复间隔(PRI)步进频率信号，可产生用于运动目标检测的低旁瓣多普勒谱，增大距离和速度检测范围。文献[12]将认知雷达引入到RSF信号中，通过波形优化设计重构目标的准确信息。文献[13]用压缩感知RIPless准则对随机PRI-SF和RSF波形进行参数优化，这种优化方法不仅能以很高概率准确重构目标一维距离像，还可实现发射信号模糊函数的优化。文献[14]针对调频步进频雷达距离像栅瓣问题提出了一种基于子带加窗的调频步进频波形参数设计优化方法，通过仿真验证了波形设计准则对提高成像质量的作用。

在步进频率杂波抑制方面，文献[15]提出步进频率雷达在进行高分辨处理时，运动目标会发生图像平移，移出杂波区，进而实现目标检测，但会导致目标信息发生变化。文献[16]提出发射步进频率信号时，在每个频率处发射2个载频相同的脉冲，先对同频的2个脉冲进行相消处理，再进行步进频率成像抑制杂波，但该方法会导致像的清晰度变差。文献[17]提出利用不同帧距离图像相减的方式抑制杂波，但成像时间较长，数据处理量较大。

可以发现，步进频率的波形设计考虑的主要问题是准确还原成像目标的信息和提高分辨率，较少考虑杂波抑制问题，在强杂波环境中成像质量较差。步进频率杂波抑制问题一般通过后处理的方式加以解决，通过波形设计抑制杂波的方案较少得到考虑，信号处理和数据处理工作量大。

本文提出了一种抑制杂波的步进频率(CS-SF)新波形。CS-SF能在波形设计上抑制杂波，其基本思想是在一维距离像合成之前利用多普勒信息进行相应的加权处理，抑制与目标速度不同的杂波，在抑制杂波的同时准确还原目标信息。

1 步进频率信号合成处理

步进频率信号属于相参脉冲串信号，每个脉冲的频率在中心频率基础上均匀步进，通过离散傅里叶逆变换(IDFT)合成大带宽获得高距离分辨率。设步进频率波形的脉冲宽度为T，脉冲重复周期为Tr，起始载频为f0，步进频率间隔为Δf，频率步进数为M。与雷达相距R1的静止散射点经过混频、低通滤波后的第i个回波信号为

(1)

式中：t为系统时间；c为光速。混频后的信号在t=iTr+2R1/c处采样，得到

i=0,1,…,M-1

(2)

式中：Ai为第i个回波信号混频后的幅度。

M个目标回波相当于一组逆傅里叶变换基，利用IDFT来实现步进频率回波信号的合成处理。对上述采样序列做IDFT处理，取模得到[18]

l=0,1,…,M-1

(3)

至此便完成了步进频率信号的脉冲相参合成处理。脉冲处理后的结果为sinc函数型窄脉冲，主瓣宽度为(1/MΔf)，距离分辨率提升了M倍。

2 抑制杂波的步进频率波形

2.1 信号模型

传统的步进频率波形合成处理无法抑制杂波。为提高信杂比，减少杂波对目标检测的影响，提出一种CS-SF新波形，如图1所示。该波形共有M组步进频率脉冲串，每组脉冲串包含N个脉冲，组内脉冲频率相同，组间脉冲频率步进。抑制杂波的基本思想是利用杂波和目标的速度差异对组内N个同频回波加权抑制杂波，之后进行步进频率距离拼接处理，从而有效提高信杂比。

图1 CS-SF波形示意图Fig.1 Schematic diagram of CS-SF waveform

CS-SF波形发射信号的第m组第n个脉冲可表示为

st(m,n)=Atexp[j(2πfmt+θm,n)]

(4)

式中：At为第m组第n个发射脉冲的幅度；θm,n为第m组第n个发射脉冲的初相；fm=f0+mΔf，表示第m组脉冲的频率。则接收信号的第m组第n个目标回波可表示为

sr(m,n)=A0exp{j[2πfm(t-τ0)+θm,n]}

(5)

式中：A0为第m组第n个目标回波的幅度；τ0=2R/c，表示回波相位延时；R=R0-v0t，表示雷达与目标的距离，其中，R0为雷达与目标的初始距离，v0为目标速度。回波信号与exp[j(2πfmt+θm,n)]混频、低通滤波后可得

(6)

若回波中同时包含目标和杂波，则回波信号可表示为

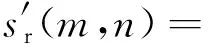
(7)

式中：Aq为第q个杂波的幅度；τq=2(Rq-vqt)/c，表示第q个杂波的相位延时；Rq为第q个杂波与雷达的距离；vq为第q个杂波的速度；fd0=2v0fm/c，表示目标的多普勒频率；fdq=2vqfm/c，表示第q个杂波的多普勒频率。在t=(mN+n)Tr+2R0/c处进行采样后得

(8)

步进频率信号属于速度敏感信号，只有进行速度补偿后，IDFT才能获得目标的一维距离像。速度补偿的目的是抵消式(8)中的速度附加相位，对于目标来说即fd0[(mN+n)Tr+2R0/c)]，对于杂波来说即fdq[(mN+n)Tr+2R0/c)]，目标与杂波在速度附加相位上有所差异。为抑制杂波，我们可利用由目标速度产生的一组加权系数对同一组内的信号进行加权处理，仅使目标部分完成速度补偿，加权系数为

wr(m)=[exp{-j2πfd0(mNTr)},

exp{-j2πfd0[(mN+1)Tr]},…,

exp{-j2πfd0[(mN+N-1)Tr]}]T

(9)

系数加权矩阵的实质是速度滤波器，下节将对此进行具体分析。假设各脉冲回波的幅度相等且为1，则经过加权处理后的信号可表示为

yr(m)=sr(m)·wr(m)=

(10)

式中：第一项表示同组内目标回波的加权积累；第二项表示同组内杂波的加权积累。第一项中fd0≪f0+mΔf，以Ku波段雷达为例，假设f0=17 GHz，Δf=5 MHz，当目标速度为2 000 m/s时，则有fd0=0.23 MHz，满足fd0≪f0+mΔf。式(10)可化简为

yr(m)=sr(m)·wr(m)≈

yc(m)

(11)

式中：yc(m)为第m组信号经过加权处理后的杂波相位项。目标回波经过加权后变为相参信号，M个综合脉冲相当于一组逆傅氏基，经过IDFT后有

l=0,1,…,N-1

(12)

式中：θl为与一维距离像无关的固定相位。取模可得

l=0,1,…,M-1

(13)

而杂波部分不是相参信号，加权系数矩阵无法完成相参积累，对同组内N个脉冲进行加权后，杂波能量增益将小于目标能量增益，从而达到抑制杂波的效果。由传统的步进频率信号得到的一维距离像为

l=0,1,…,M-1

(14)

因此，该波形可使信号幅度提升N倍。

CS-SF信号处理算法的基本思想是利用组内加权抑制杂波，利用组间IDFT获得目标一维距离像，处理流程如下：

1)利用速度估计算法或先验知识得到目标估计速度v；

2)计算组内脉冲的加权系数wr；

3)对各组脉冲进行加权处理，得到M个步进频率综合脉冲；

4)对M个综合脉冲进行IDFT一维距离像拼接，得到一维距离像。算法处理流程如图2所示。

图2 算法流程Fig.2 Algorithm flowchart

2.2 杂波抑制原理

CS-SF波形利用加权系数矩阵抑制杂波，其具体表达式如式(9)所示。通过步进频率速度估计算法得到目标的速度估计值，然后利用式(9)即可获得加权系数矩阵。加权系数矩阵实际上是速度的带通滤波器。对加权系数矩阵做频谱分析，其频谱为

l=0,1,…,N-1

(15)

由式(15)可知，加权系数矩阵实际为一个sinc函数型的速度滤波器，其主瓣宽度为λ/(2NTr)，因速度滤波器存在凹口和峰值，故信杂比改善并不随速度差异单调变化。当目标和杂波的速度差位于速度滤波器的凹口时，信杂比改善效果较好；当目标和杂波的速度差位于速度滤波器的峰值时，信杂比改善效果较差。可通过改变CS-SF的波形参数获得不同的速度滤波器，提高信杂比改善值。

计算CS-SF的加权系数矩阵需要目标的速度信息。传统的步进频率信号是速度敏感信号。目标的运动会引起一维距离像的平移和发散失真，需要通过速度估计获得目标的估计速度，经过速度补偿后才能获得目标的一维距离像。

速度补偿需要满足一定的精度要求，假设目标速度为v0，则第i个脉冲的目标时延为

(16)

则式(2)变为

i=0,1,…,M-1

(17)

经过IDFT展开相位部分并忽略常数项可得

(18)

式中：第一项为距离相关项；第二项为一次相位误差，该项将造成一维距离像平移，假设一次相位误差可容忍的测距精度为半个合成后的距离单元，则|Δv|≤c/(4Mf0NTr)；第三项为极小相位误差，可忽略；第四项为二次相位误差，该项将造成一维距离像的展宽，假设可容忍的二次相位误差为π，则|Δv|≤c/(4M2ΔfNTr)。一般情况下，f0≫MΔf。因此，速度估计误差应满足|Δv|≤c/(4Mf0NTr)[19]。

对于CS-SF波形，假设当前目标速度估计值为v+Δv，则第m组脉冲加权后的综合脉冲为

yr(m)=sr(m)·wr(m)=

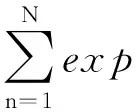
(19)

同组内脉冲的最大相位误差为4π(f0+mΔf)ΔvNTr/c，假设同组内脉冲允许的最大相位误差为π/2，则速度误差应满足的条件为

(20)

一般情况下，M≥2，即c/(4Mf0NTr)≤c/(8Nf0Tr)。因此，在传统步进频率速度补偿精度的要求下，CS-SF组内脉冲积累的速度精度也可得到满足。

3 仿真结果及分析

仿真场景设置如图3所示。机载雷达与目标相向运动，目标位于雷达波束主瓣照射范围内，目标回波的多普勒明显大于主瓣杂波的多普勒。不失一般性，设机载雷达的速度为120 m/s，目标的速度为600 m/s，雷达与目标和杂波的相对速度可利用角度关系获得。假设波束俯仰角为30°，则雷达与目标的径向速度约为600 m/s，雷达杂波的速度约为100 m/s。目标距离R0=350 m，杂波距离Rq=280 m。

图3 仿真场景设计Fig.3 Design of simulation scene

相控阵仿真雷达平台的指标参数为：盲区距离Rblind=30 m，最大不模糊距离Rmax=1 500 m，距离分辨率ΔR=0.12 m。仿真波形参数需满足平台指标，脉冲重复周期Tr需满足Tr≥2Rmax/c=10 μs，步进频率Δf与频率步进数M需满足MΔf=ΔR，脉冲宽度T需满足T≤2Rblind/c=0.2 μs。

较传统步进频率波形而言，CS-SF波形处理后的目标幅度有N倍的提升。为保证2组波形目标幅度一致，需将CS-SF波形发射功率降低为传统步进频率波形的1/N，采用的方法为将CS-SF波形脉冲重复周期设置为传统步进频率波形的1/N。该设置对信杂比并无影响。

在传统步进频率波形仿真中，设步进频率信号的脉冲重复周期Tr=160 μs，步进频率Δf=5 MHz，载频起始频率f0=10 GHz，脉冲宽度T=0.2 μs，频率步进数M=256，脉冲归一化幅度A=16，估计速度v=600 m/s。在CS-SF波形仿真中，设步进频率信号的脉冲重复周期Tr=10 μs，步进频率Δf=5 MHz，载频起始频率f0=10 GHz，脉冲宽度T=0.2 μs，组内脉冲数N=16，频率步进数M=256，脉冲归一化幅度A=1，估计速度v=600 m/s。传统步进频率波形成像结果如图4(a)所示，目标幅度为57.86 dB，杂波幅度为33.96 dB，信杂比为23.90 dB。CS-SF波形成像算法处理结果如图4(b)所示，目标能量为57.99 dB，杂波能量为12.41 dB，信杂比为45.58 dB，信杂比改善值为21.55 dB。

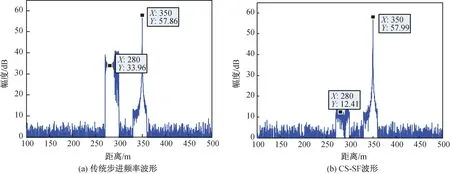
图4 一维距离像Fig.4 One-dimensional range image

CS-SF波形所用到的加权系数矩阵频谱如图5所示。经过加权系数矩阵处理后，相当于对目标速度为600 m/s处的脉冲进行相参积累，积累增益为20×lgN=24.08 dB。由于速度失配，使得杂波积累增益相应降低。当杂波速度为466.3 m/s时，杂波积累增益为10.94 dB，信杂比改善值为13.14 dB，仿真数值为13.35 dB。当目标速度为507.3 m/s时，杂波积累增益为-19.89 dB，信杂比为43.94 dB，仿真数值为43.26 dB。题设中杂波速度为100 m/s，由图可知，杂波能量降低理论值应为24.02 dB，与实际值21.55 dB符合得较好。

图5 系数加权矩阵频谱Fig.5 Spectrum of coefficient weight matrix

实际目标并不全是单散射点目标，大部分是扩展目标。利用实际扩展目标模型进行系统仿真验证。仿真中目标距离范围为340～372 m，速度范围为595～605 m/s，杂波距离范围为320～400 m，速度范围为80～120 m/s。仿真中传统步进频率波形和CS-SF波形参数设置保持不变。系统仿真结果如图6所示。图中：虚线表示传统步进频率波形处理结果，实线表示CS-SF波形处理结果，在保持一维距离像不发生平移和失真的前提下，信杂比改善值约为21 dB。由图可见，CS-SF波形能在保证一维距离像不失真的情况下抑制杂波，改善信杂比，提高高分辨雷达宽带一维距离像成像性能，有利于后续的检测和处理。

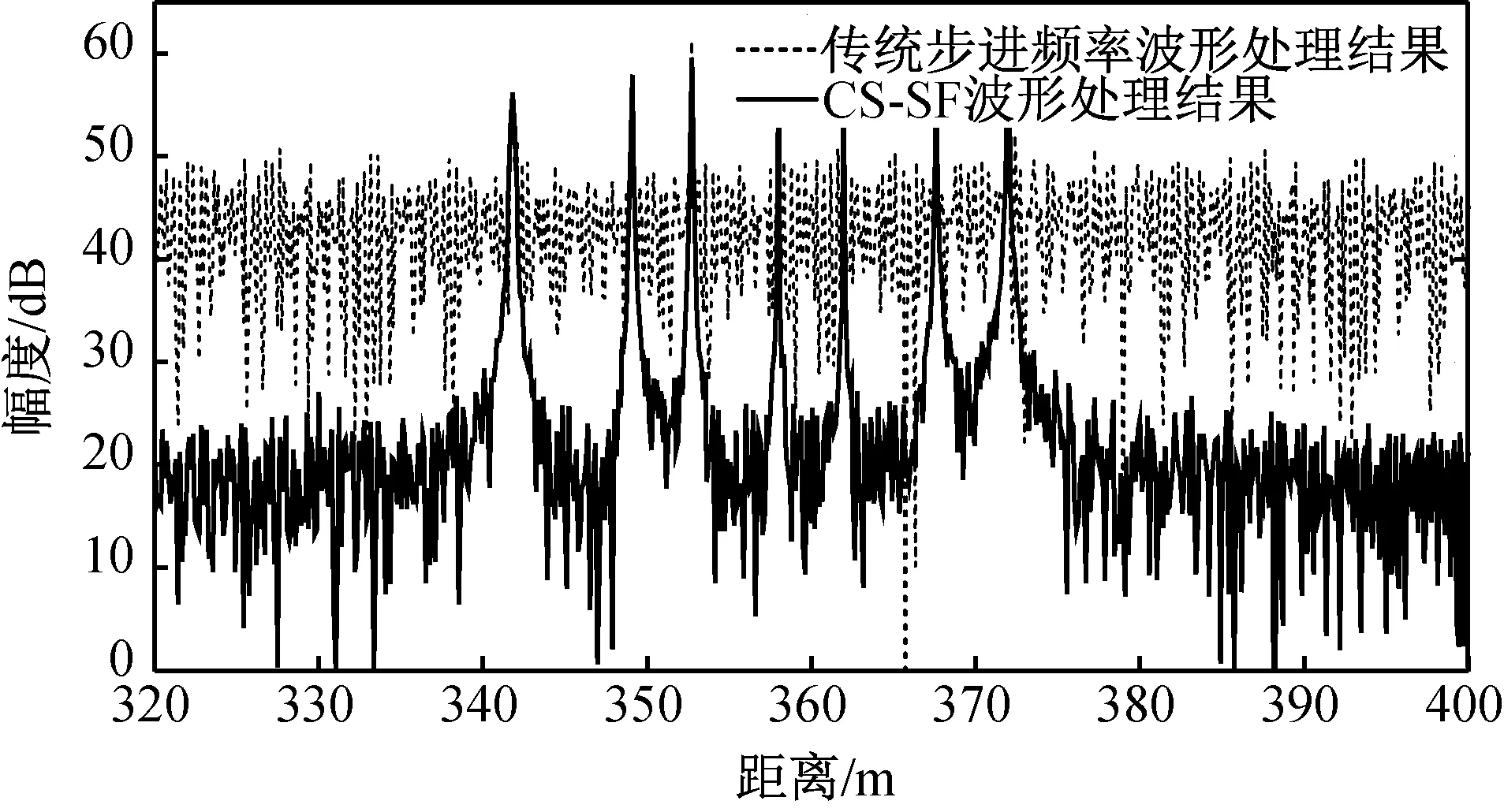
图6 系统仿真结果Fig.6 Results of system simulation

从系数加权矩阵频谱中可以观察到，CS-SF波形的实际效果受目标估计速度影响较大。当目标估计速度偏差较大时，目标可能会位于系数加权矩阵频谱的凹口处，其增益低于杂波，造成目标检测困难。因此，CS-SF波形在实际应用中需与高质量的速度估计算法结合使用。

仿真表明：CS-SF波形能在提高信杂比的同时准确还原目标信息，且处理复杂度较低，处理数据量较小，适用于机载雷达一维距离成像。

4 结束语

传统步进频率波形进行一维距离高分辨成像时，强杂波可能会造成目标点掩盖和虚假目标点，影响目标检测。CS-SF波形可有效抑制杂波。该波形共发射M组频率步进的脉冲，每组包含N个载频相同的脉冲，通过组内脉冲加权抑制杂波，得到M个杂波抑制后的综合脉冲，最后对M个综合脉冲进行IDFT获得高距离分辨率，组内加权系数矩阵通过目标估计速度获得。加权系数矩阵的物理含义是速度滤波器，可在理论上计算信杂比改善值。同时，与传统步进频率波形相比，CS-SF波形无需提高速度估计精度即可完成杂波抑制。最后通过仿真说明CS-SF波形抑制杂波的有效性，信杂比改善实际值与理论值基本符合。虽然CS-SF波形能有效抑制杂波，但因发射脉冲被分割，不模糊距离减小为1/N，同时探测距离也有所减小，故适用于近距离杂波抑制。相比于普通的步进频率波形，CS-SF波形能更好地抑制杂波，降低数据处理复杂度，还原目标一维距离像，为机载雷达在强地杂波背景下准确检测目标和还原目标信息提供新思路，在高分辨距离成像方面具有一定的工程应用价值。速度估计算法与CS-SF波形的结合将是后续研究的重要主题。