星载线阵CCD相机与激光测高仪无控定位精度对比分析

黄朝围，何赟晟，孙凯鹏，李国元，徐 毅

(1.上海卫星工程研究所，上海 201109； 2.国家测绘地理信息局 卫星测绘应用中心，北京 100180)

0 引言

随着计算机、通信及信息处理技术的发展，高分辨率卫星摄影测量技术逐渐满足中等到大比例尺测图的技术要求。高分辨率卫星摄影测量技术能快速、大面积地获取地球空间信息，实时更新我国乃至全球的大比例尺地形图，拥有传统测绘手段不具备的现势性。近年来，国内外高分辨率立体测图卫星的发展势头迅猛，如：从胶片返回式卫星到传输型卫星；从框幅式相机到单线阵、双线阵乃至三线阵相机；从百米量级分辨率到亚米级分辨率；从百米级的无控制定位精度到米级无控制定位精度。其中多线阵推扫式相机拥有较高的基高比和优秀的成像品质，是高分辨率立体测图卫星的主要发展方向[1]。

2012年发射的“资源三号”卫星携带3台线阵CCD相机，前、后视地面分辨率3.5 m，正视分辨率优于2.1 m，无控定位精度优于15 m；有控定位精度中，平面精度优于4 m，高程精度优于3 m[2]。立体测图卫星拥有诸多优势，同时也受到许多条件限制。卫星内、外方位元素存在系统误差，使无控定位精度受到影响，需要加入观测区域控制点予以修正，才能满足1∶50 000比例尺测图的精度要求。日本ALOS宣称以无控定位完成1∶25 000比例尺立体测图，但实际在轨运行结果没有达到指标要求。王任享[3]通过定量分析证明，仅通过提高相机分辨率不能有效提高定位精度，姿态测量误差对高程精度的影响很大，无地面控制点摄影测量卫星要想达到更高比例尺(1∶10 000)的测图要求，尚有难度。

星载激光测高系统通过搭载在卫星上的激光测距仪，能以较高精度获取星下点的高程信息，在天体特征研究中已有较成熟的应用，例如月球探测、火星探测、水星探测等深空探测工程[4-5]。美国2003年发射的对地激光测高卫星(ICESat)，搭载激光测高系统(GLAS)，其在平坦地区的测高精度小于3 cm[6]。激光测高仪发射的脉冲有一定的发散角，到达地面后形成直径几十米的光斑，高程值在光斑内的位置难以确定，GLAS的平面定位精度在10 m量级[7]，因此星载激光测高系统的水平定位精度较低。

高分辨率线阵相机摄影测量卫星与激光测高卫星各具优势，同时也各有缺陷。将两者结合，形成互补，将有效提高卫星无控制点定位精度[8-9]。本文构建两者的几何定位模型，基于定位模型推导误差传播方程，通过仿真参数，对比分析两者在同平台下的定位精度，可为提升遥感卫星无控定位精度的相关研究提供参考。

1 定位模型对比

1.1 立体影像前方交会定位模型

星载线阵CCD相机采用推扫式成像，通过线阵CCD获得连续的影像条带，记录外方位元素，每行扫描影像与被摄物体之间具有严格的中心投影关系。前、下、后视任两者对同一地面位置获取的影像形成立体相对，可用前方交会法解算地物点的坐标。本文以前、后视为研究对象讨论星载线阵立体相机的无控定位精度。线阵相机前方交会定位几何示意图如图1所示。

图1 线阵相机前方交会定位几何示意图Fig.1 Forward intersection of line-array CCD camera

立体像对前方交会定位模型为

(1)

(2)

(3)

式中：(Xm，Ym，Zm)为地面点在摄影测量坐标系上的坐标；(XS1，YS1，ZS1)、(XS2，YS2，ZS2)为左、右相机摄影中心点在地面摄影测量坐标系上的坐标，即相机的外方位线元素；N、N′为左、右像点的投影系数；BX、BY、BZ为摄影基线在地面摄影测量坐标系上的3个分量；(X1，Y1，Z1)、(X2，Y2，Z2)为像点在像空间辅助坐标系上的坐标，与像点坐标的关系为

(4)

式中：(x1，y1，-f)和(x2，y2，-f)为左右影像的像空间坐标；R1和R2为像空间坐标系与像空间辅助坐标系的转换矩阵[10]。

1.2 激光测高卫星定位模型

激光发射器发射一束激光脉冲，激光光束穿透大气层照射到地面形成光斑，经光斑覆盖区域内地表反射后，部分激光光子由大气层返回，被激光测高仪上的望远镜接收。测高仪精确测定激光的往返传播时间，用光速乘以激光的单程传播时间，得到测高仪的激光发射点到地面光斑的距离ρ。通过星上指向测量系统测得激光束相对于卫星平台的指向角，由此得到卫星平台坐标系上的激光测距向量ρ。星上的定位测量单元主要由GPS接收机组成，通过测量得到卫星质心在国际协议天球坐标系(ICRS)上的位置。通过星敏及陀螺获得卫星姿态，通过姿态转换将卫星平台坐标系下的激光测距向量ρ、激光发射参考点的偏心量ΔPref、GPS天线相位中心偏心量ΔG转换至协议天球坐标系上[11]。利用卫星位置向量、激光测距向量、偏心量及光斑位置向量rspot之间的几何关系，建立几何定位模型，如图2所示，图中rg为卫星位置向量。

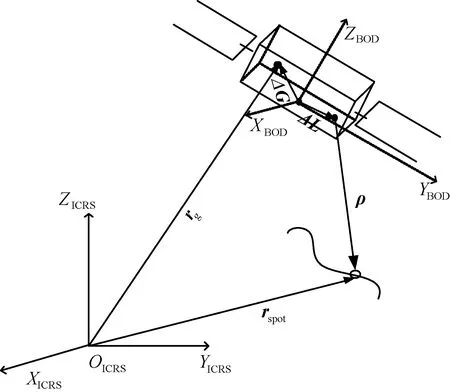
图2 激光脚点定位几何示意图Fig.2 Schematic diagram of laser footprint positioning

激光测高卫星几何定位模型为

(5)

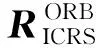
为简化计算，忽略轨道系向天球系的转换过程，直观地研究主要观测量对定位精度的影响，对模型做出调整。以卫星向径与地面的交点为原点，定义站心坐标系(STA)，坐标轴平行于轨道坐标系的坐标轴。将轨道坐标系直接转换至站心坐标系，对站心坐标系上的激光脚点定位模型进行分析。简化后模型为

(6)

2 误差源及定位精度评定方法

星载线阵CCD与激光测高仪的定位精度受到诸多因素的影响，这些因素来自于卫星的各个测量设备及有效载荷，包括依靠GPS接收机的精密定轨系统、依赖于陀螺仪及星敏感器的定姿系统、线阵CCD相机及激光测距仪等。这些测量设备的测量误差及安装关系共同作用，决定最终的定位精度。进行精度评定时，星载线阵相机主要考虑以下误差影响：

1)外方位元素的测量误差，即卫星位置和姿态的测量误差；2)星敏及相机的视轴指向受空间环境影响而导致的缓变误差；3)内方位元素的测量标定误差；4)像点测量误差；5)时间同步误差。

影响激光测高卫星定位精度的主要误差为：

1)卫星位置及姿态测量误差；2)激光测距误差；3)激光指向角测量误差；4)时间同步误差。

考虑以上主要误差项对目标地面点的定位精度影响，首先推导误差传播方程。

2.1 立体影像前方交会定位的误差传播方程

根据立体影像前方交会定位模型，其定位精度受左右影像的内外方位元素测量误差及像点测量误差的影响，分别对各测量误差求偏微分，推导前方交会定位的误差传播方程，有

(7)

卫星平台通过姿态控制系统，保持稳定的飞行姿态。偏航角κ、俯仰角φ和横滚角ω的数值很小，像平面坐标到像空间辅助坐标的转换矩阵可简化为

(8)

可认为

(9)

则

x1=-x2=ftanα

(10)

式中：f为相机焦矩；α为前、后视与正视相机光轴的夹角。

认为前后视相机的内外方位元素和像点坐标的测量误差是相等的，用式(11)求前方交会定位的精度，有

(11)

式中：mXm、mYm、mZm分别为前方交会定位误差；mXS1、mYS1、mYS1分别为相机摄影主点的定位误差；mBX、mBY、mBZ分别为摄影基线分量误差，可通过卫星的飞行速度和计时精度或前后视相机摄影主点的定位误差求出；mκ、mφ、mω为姿态角误差；mx、my为像点测量误差(包含内方位元素测量误差)；mf为相机焦距的测量误差；H为轨道高度。

2.2 激光测高系统脚点定位误差传播方程

激光脚点定位模型是观测值L=(κ,φ,ω,ρ,α,θ,Xg,Yg,Zg)的非线性函数，现对模型的定位精度进行评定。对模型用泰勒级数展开至一阶项，根据误差传播定律，进行精度评定。模型的泰勒级数展开如下：

(12)

式中：dL=(dκ,dφ,dω,dρ,dα,dθ,dXg,dYg,dZg)。

令

(13)

则由式(6)，站心坐标系上激光脚点定位模型可表示为

(14)

由于姿态角数值较小，可简化姿态转换矩阵。

各自求偏导数后，假设9个观测值相互独立，观测的中误差分别为mκ、mφ、mω、mρ、mα、mθ、mXg、mYg、mZg，脚点坐标的误差为mX，mY，mZ。根据误差传播定律，站心坐标系上激光脚点坐标的误差为

(15)

3 定位精度估算与对比分析

3.1 定位精度估算

为比较2种测量手段的优缺点，假设2种观测载荷搭载于同一卫星平台上，分析比较两者的定位精度。卫星轨道为太阳同步轨道，轨道高度为505.984 km，载荷参数设计见表1。

星载激光测高仪的激光发射点偏心量、GPS天线相位中心偏心量均为固定偏差，在轨经一次检校后可消除。激光指向为天底方向，激光测距值ρ近似取轨道高。根据表1中的卫星参数，分别用式(11)、(15)计算2种观测方式的误差传播系数。线阵CCD相机定位误差计算方程为

表1 载荷设计参数

(16)

激光测高仪定位误差计算方程为

(17)

为便于直观理解各项观测误差对定位精度的影响，将mx、my、mf分别乘以10-6，mω、mφ、mκ分别乘以π/(3 600×180)。从式(16)可得，1 μm的像点测量误差会造成X轴方向上约0.21 m的误差，1″俯仰角误差会造成X轴方向约2 m的误差。

卫星的轨道及姿态是定位解算的关键，由于星上测量结果存在较大误差，因此需要下传原始观测数据，通过地面处理提升精度，地面精密定轨精度可达厘米级，当前卫星定轨精度可达0.05 m[12]。地面结合星敏、陀螺及角位移参数，通过组合卡尔曼滤波进行精密定姿，姿态测量精度(随机误差)可达角秒级，取姿态测量精度为1″。测绘卫星采用GPS秒脉冲作为统一授时基准，时间同步误差可达50 μs以内，其对定位精度的影响等同于卫星沿轨道位置计算偏差0.35 m。为确定相机指向，需对相机视轴与星敏视轴的夹角进行标定，受轨道热环境变化的影响，星敏和相机视轴产生缓慢性的角度变化，对于测绘任务而言具有系统性和随机性，难以通过定标或数学方法消除，这种情况是影响无控定位精度的主要因素之一，设该误差值为3″。相机镜头及探测器受主动段及空间环境的影响产生系统性的内畸变，在轨利用检校场进行精密内定标，主点标定误差0.3个像元，主距标定误差20 μm[14]，通过自主精密温控等措施，相机的内方位元素将具备较高的稳定性[13]。线阵CCD相机的像点测量误差取经验值0.36个像元。激光测高仪发射主动激光光源，可通过地面布设靶标等手段进行激光指向的标定，指向测量精度取3″。星地测距精度取决于对脉冲传播时间的测量精度，星载激光测高仪测距精度可达厘米级，本文设该项误差为0.5 m。各项误差的取值汇总见表2。

表2 卫星平台及载荷的各项测量误差

摄影基线分量误差根据摄站点定位误差计算，有

(18)

像点测量误差与主点误差引起的定位误差一致，合并一项考虑，有

(19)

根据以上卫星载荷参数及观测指标，分别用式(16)、(17)计算2种方式的定位精度，见表3。

表3 线阵CCD相机及激光测高仪定位精度估计

从定位精度对比可看出，在同平台上，激光测高仪的高程精度远优于线阵CCD相机前方交会定位的高程精度。平面定位精度理论上为同一量级，但由于地面激光光斑直径为30 m，实际平面定位精度应在31 m以内。

3.2 对比分析

对于星载线阵CCD相机，精密定轨精度达到厘米级，不再是影响定位精度的主要因素。影响相机平面定位精度的主要因素是姿态角误差和像点测量误差，影响其高程精度的主要因素是俯仰角误差、像点测量误差和焦距误差。通过改变定姿精度和相机地面分辨率，分析姿态角误差和像点测量误差对定位精度的影响，结果见表4。由表4可知，对于星载线阵相机，相机分辨率的变化对定位精度，尤其是测高精度的影响不明显，仅通过提高相机分辨率无法达到提高定位精度的目的。制约其定位精度的主要因素是姿态角误差，其中，测高精度主要受俯仰角误差影响。

对于激光测高仪，影响其平面定位精度的主要因素是姿态角误差和激光指向角误差，影响其测高精度的主要因素是激光测距误差。从表5和图3可知，当激光指向角为0°时，测距误差约等于测高误差，随着指向角增加，指向角及姿态角(横滚角)误差会带来明显的测高误差，且误差值随指向角增大而增大。指向角较大时，姿态角及指向角误差成为引起测高误差的主要原因之一，因此激光指向采用天底方向可提高星载激光测高的测高精度。同时，激光测高仪的平面定位精度还受到激光光斑(即发散角)大小的影响，在满足回波信号探测的前提下，应尽可能降低激光发散角。

对比表4、5的定位精度可知，2种遥感方式的平面定位精度均受姿态角测量误差的影响。当激光指向为天底或小角度偏离星下点时，激光测高仪的测高精度主要受测距误差和定轨的径向误差影响，卫星精密定轨精度已达厘米级，国产星载激光测距仪精度也达到1 m以内，因此国产星载激光测距仪的测高精度预期小于1 m。立体相机的测高精度对姿态角(俯仰角)误差及星敏与相机间的安装角度变形非常敏感。而卫星热稳定性及结构稳定性控制技术的提升并非易事，仅通过提升分辨率，对提高立体相机的测高精度作用较小。因此，姿态角误差及星敏与相机间的安装角度变形已成为实现无控1∶50 000以上大比例尺光线测图卫星的瓶颈。相比星载线阵CCD相机，星载激光测高仪在测高方面具有先天优势。

表4 像元尺寸及定姿精度对线阵CCD相机前方交会定位精度的影响

表5 激光指向角度及定姿精度变化时的激光测高仪定位精度

图3 不同指向角度时激光指向测量误差引起的高程误差Fig.3 Altitude error caused by pointing error at different attitudes

4 结论

本文推导了星载线阵CCD相机及激光测高系统的定位模型和误差传播方程，通过设定卫星及载荷参数，利用误差传播方程，在同平台下估算两者的无控定位精度，并进行对比分析，有如下结论：

1) 同卫星平台下，线阵CCD相机的平面定位精度高于激光测高仪，后者的高程精度高于前者。

2) 目前技术水平下，姿态角误差是影响星载线阵相机定位精度的主要因素。相机分辨率(或像元尺寸)对定位精度的影响相比姿态角误差要小，因此通过提高相机分辨率无法有效提升定位精度。

3) 星载激光测高仪的高程精度主要取决于测高仪的测距精度，因此其测高精度较高。平面定位精度主要取决于姿态角测量精度、指向角测量精度和光斑大小，平面定位精度较低。

2种遥感方式各具优势，也有各自的不足。本文从理论上估算两者的无控定位精度。线阵CCD相机通过前方交会实现立体测绘，但其高程测量对姿态确定精度要求极高。星载激光测高仪发射的激光脉冲存在一定的发散角，在地表形成一个直径数十米的光斑，测高值拥有较高的精度，但高程在光斑内的位置难以确定，平面精度低，且激光发射重频低，获取的探测结果为稀疏的离散点位信息，无法实现对目标成像。

将2种遥感手段进行结合，可提升测绘卫星的无控定位精度，有2种途径：一是研制发射专用的激光测高卫星，获取高精度全球高程控制点，建立高程控制点库，通过联合平差处理提升光学卫星的测高精度，国内已有研究表明这种多源卫星数据融合的方法能显著提升测图的高程精度[15]；二是在卫星上同时搭载线阵CCD相机和激光测高仪，获取可见光影像及高精度高程点，激光光斑通过足印相机实现与可见光影像的精确匹配，激光足印作为平面及高程控制点参与平差，实现高精度立体测图，目前国内已有在研卫星型号采用该体制，力图实现1∶10 000全球无控立体测绘。随着技术的进步，激光测高仪逐渐向微脉冲高重频方向发展，进一步缩小激光光斑。未来专用激光测高卫星将获取更高精度、更密集的全球控制点，可与海量光学卫星影像进行数据融合，提升测绘产品精度，充分发掘光学卫星影像的应用价值。