永磁同步电机驱动的机器人哈密顿与PD协调控制

徐 旭，于海生，于金鹏，刘旭东，吴贺荣

（青岛大学 自动化与电气工程学院，青岛 266071）

0 引言

作为当今工业领域最常见的工业机器人之一的关节机器人，主要表现形式为工业机械臂，在自动化装配领域应用广泛。永磁同步电机（PMSM）广泛的应用于机器人关节驱动系统中，得益于其具有良好的可控性能、结构简单、调速范围宽、准确度高、噪声低等特点[1]。当前应用于机器人驱动系统的控制方法中，比例微分（PD）控制方法应用广泛、设计简单，但受参数影响较大，而且抗干扰能力较差，很难广泛的应用于实际工程当中去；拉格朗日公式法可以推导出机器人动力学一般形式模型，有效解决了多关节机器人动态建模问题，适用于大部分机器人动力学求解问题[2,3]，但推导过程相对麻烦，而且很难和机器人驱动电机控制相结合；鲁棒自适应控制能够有效解决系统模型中不确定性问题，能够实现对机器人关节位置及速度的有效跟踪，既能够保证不确定系统的稳定性而且能够根据实际系统的需求修正控制规律及参数[4,5]，但是设计复杂；文献[6]提出一种简单的滑模控制方案，不依赖独立稳定的不连续曲面，减少了设计的复杂性；文献[7]介绍了一种基于干扰上界的滑模控制，但单纯的滑模控制消除不了抖振问题；文献[8]设计基于反馈线性化控制算法，具有良好的控制效果，但是忽略非线性部分的线性化模型将不再能反映系统特性；神经网络自适应控制可以逼近机器人动态模型，有效解决复杂的机器人控制系统的非线性和不确定性，使机器人在理想动态下有效的跟踪给定轨迹，具有良好的控制性能[9,10]；神经网络控制通过不断的学习，使系统具有更好的适应性以及更好的动态性能[11]；模糊控制可以很好的和其他控制方法结合使用，能够实现对复杂系统的有效控制，但是信息简单的模糊存在精度低、动态品质差的缺点[12,13]；反步法设计简单，能够实现PMSM控制系统的完全解耦，可用于机器人的高精度运动控制[14,15]。基于能量受控的哈密顿方法广泛应用于永磁同步电机的控制[16,17]，为实现机器人动力学与驱动电机控制结合，本文采用哈密顿控制方法设计机器人关节位置控制器，使系统具有更好的稳态特性，但是单独采用PCH控制系统动态响应较慢，所以设计协调控制策略，与PD加重力补偿进行协调控制，此时系统既具有PD快速的动态响应，也会保持PCH控制的稳态特性；用反步法对驱动电机电流进行控制，然后通过电流转换将两个控制器结合，实现机器人与驱动电机的整体控制，而且系统具有较好的抗干扰能力。

1 机器人模型

1.1 机器人动力学与运动学模型

n关节机器人拉格朗日动力学方程可表示为[18]：

式中，q为n维关节转动角位移向量；为n维关节转动角速度向量；为n维关节转动角加速度向量；D(q)∈Rn×n为对称正定惯性方阵；为哥式力与离心力矩阵；Rf为摩擦阻力系数矩阵，G(q)∈Rn为重力矩向量；τ为输入力矩向量。

两关节机器人如图1所示，L1、L2分别为关节机器人的两个关节长度，q1、q2分别为两个关节的角位移，m1、m2分别表示两个关节的质量。

图1 两关节机器人空间坐标示意图

式(1)中参数矩阵和向量可求得为：

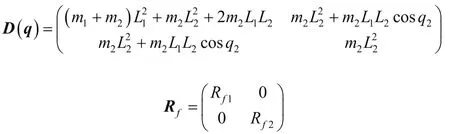
机器人末端C点与基座A点的关系可表示为：

式中，c12=cos(q1+q2)；s12=sin(q1+q2)；s1=sinq1；c1=cosq1。

由机器人末端期望位置(xd,yd)，根据机器人逆运动学，可分别求得两个关节的角位移：

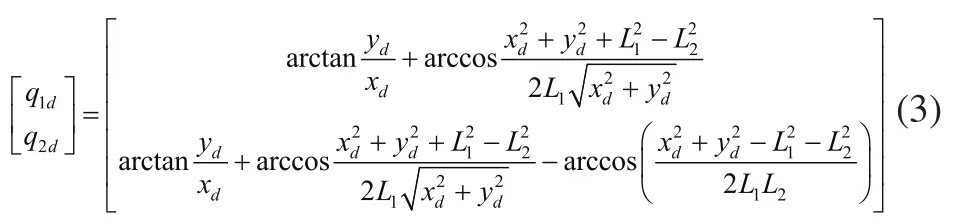
1.2 PMSM数学模型

PMSM在d-q坐标系下数学模型[19]：

式中，i=1,2；Lid和Liq分别d轴和q轴的定子电感；iid和iiq分别为d轴和q轴的定子电流；uid和uiq分别为d轴和q轴的定子电压；Ris为定子电阻；nip为极对数；wi为转子机械角速度；Jim为转动惯量；τiL为负载转矩；Φi为永磁同步电机产生的磁链；θi为永磁同步电机角位移；qi为机器人关节角位移。

2 机器人控制方案

机器人系统控制方案如图2所示，给定机器人期望的轨迹坐标，根据机器人逆运动学可求得两个关节期望的角位移，通过机器人关节位置PCH和PD控制器，分别求得到机器人关节驱动力矩，设计协调控制策略得到协调后的力矩，然后经过电流变换，采用反步法对PMSM电流进行控制，从而实现机器人与PMSM控制的有机结合。

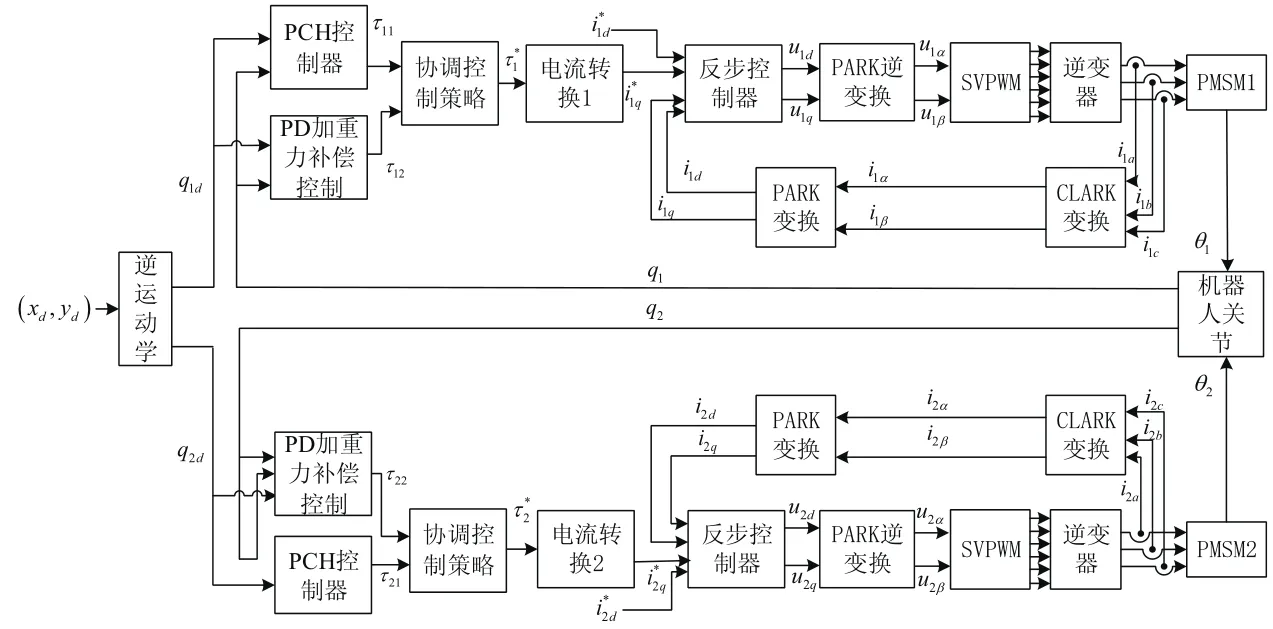
图2 二自由度关节机器人驱动系统控制框图

2.1 机器人位置协调控制设计

选取哈密顿函数为：

其中， q∈R2、p∈R2分别为角位移和动量向量，V(q)为势能，且q、p的关系可表示为：

则机器人动力学的哈密顿模型可表示为[20]：

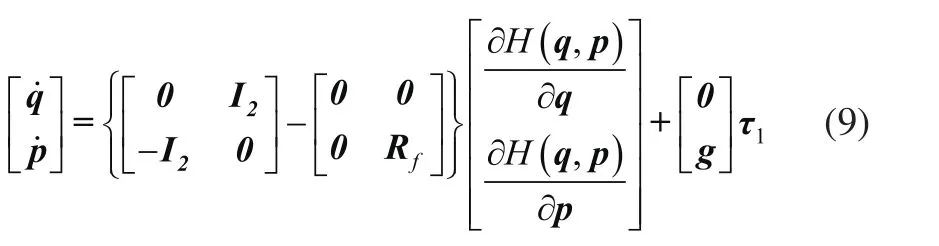
式中I2为二维单位矩阵，τ1=[τ11τ21]T为输入力矩向量，取g=diag{1 1}。

取机器人动力学系统的期望哈密顿函数：

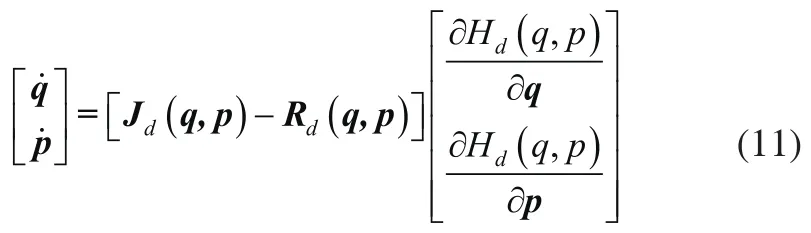
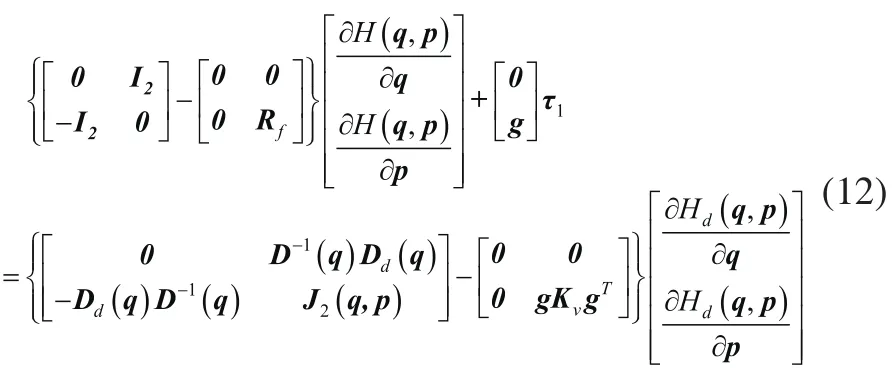
由式(12)可求得PCH控制器：

取Dd(q)=D(q)，J2(q,p)=0，可求得：

设计机器人末端位置PD加重力补偿控制器。选取PD加重力补偿控制律：

可求得PD加重力补偿控制器为：

构造协调函数：

式中C1(t)，C2(t)分别为PCH和PD加重力补偿控制器的协调参数；a，b为常数。

设计协调控制策略：

根据实际需求设定机器人关节角位移最大误差值，当，(i=1,2)时，系统投入协调。

式中Kd，Rf均为正定矩阵，，所以协调控制系统是渐近稳定的。

2.2 电流控制器设计

利用隐极(Lid=Liq)PMSM的=0控制原理可知[22]，由式(5)可求得：

利用反步法原理设计电流控制器[23,24]。

进而可求得：

进而可求得：

则电流控制器可表示为：

2.3 稳定性分析

取整个系统Lyapunov函数V=V2+V1q+V2q，由以上分析可得机器人关节位置PCH控制系统和PMSM电流控制系统均为渐近稳定，因此整个系统是渐近稳定的。

3 仿真结果

机器人参数：L1=L2=1m，m1=m2=1kg，Rf=diag{(2.1 0.3)}，Kv=diag{(10.75 6)}，ρ=1，Kp=diag{20 100)}，Kd=diag{3 10)}。PMSM参数：Lid=Liq=0.0085H，Ris=2.875Ω，nip=4，Φi=0.175Wb，Jim=0.02kg.m2，k1d=k2d=k1q=k2q=10000，a=0.2，b=0.5。机器人末端位置由点（1.5，0.5）运动到点（0.5，1.5），t=4s时系统负载转矩发生变化。由图3、图4可以看出协调控制与PD加重力补偿控制动态特性曲线几乎重合；稳态特性曲线与PCH控制几乎重合。协调控制能够很好的结合两种控制方法的优点，既具有很快的动态响应速度，而且具有一定的抗负载转矩扰动能力。

图3 机器人关节末端x轴坐标

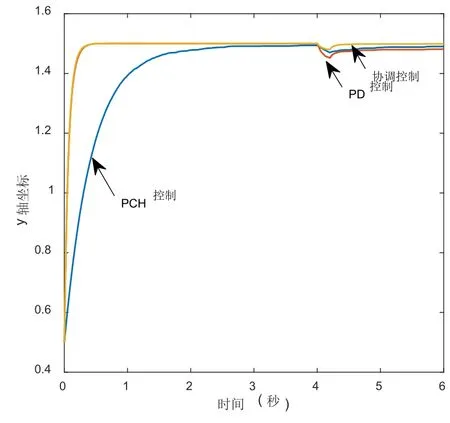
图4 机器人关节末端y轴坐标

4 结束语

本文针对二自由度机器人关节驱动系统进行研究，为提高机器人末端位置控制效果，运用依靠互联配置、阻尼注入和能量成型的PCH和PD加重力补偿控制方法分别求取机器人关节位置控制器，并设计协调控制方案；用反步法将复杂的机器人驱动电机控制系统分解为中间子系统，然后把子系统集成起来完成对机器人驱动电机进行控制，并通过电流变换将机器人关节位置控制与驱动电机电流控制相结合。由仿真结果可以看出协调控制机器人末端位置可以快速并且准确的到达期望位置，而且与PD加重力补偿和PCH控制方法单独控制做出对比，证明此方案既具有较快的动态过程，而且有更好的控制性能和抗负载转矩扰动的能力，所提出的控制方法具有很好的应用前景。

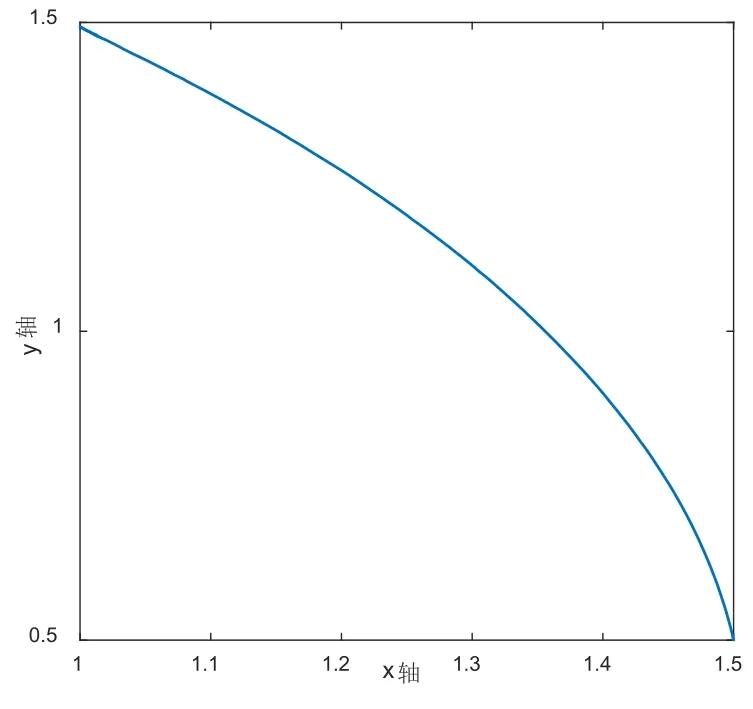
图5 协调控制关节末端轨迹

图6 协调函数曲线图