桩底盾构施工引起的桩基承载力损失计算

宫全美， 张润来， 余 杰， 周顺华

(同济大学 道路与交通工程教育部重点实验室，上海 201804)

地铁盾构隧道穿越建筑物不可避免地会下穿建筑物桩基，从而造成桩底、桩侧土应力场发生改变，会对既有建筑物桩基的变形和受力情况产生不利的影响，从而影响上部结构安全.

目前，国内外学者在隧道开挖对建筑物桩基影响研究上主要采用的方法有现场实测法、理论解析法、模型试验法和数值法.数值法由于其适应性强，分析结果详细，数据查看方便，被更广泛应用.Mroueh等[1]、Lee等[2]在有限元中分别考虑了土体应力释放因素与隧道-桩基的相互作用.朱逢斌等[3]通过数值模拟和离心试验结果的对比分析，证明了采用数值模拟的方法来进行盾构隧道开挖对邻近桩基影响的研究是可行的.霍军帅等[4]用有限元法分析盾构隧道施工对城际铁路桩基的影响并对加固方案进行分析.王卫东等[5]对有限元中桩土接触单元所采用的接触模型进了修正，将桩土界面的双曲线模型嵌套到ABAQUS软件中.袁海平等[6]用有限差分法分析盾构推进过程中不同工况下桥桩结构受力、水平变形、地层沉降的变化规律.陈明等[7]等对桩土界面的荷载传递模型进行了改进，考虑了基坑开挖引起的卸荷效应.李新星等[8]采用有限元法模拟隧道近距离穿越高架桩基的施工过程并提出保护措施.

综合目前数值分析法的研究结果，首先，主要集中在桩基变形、受力分析和盾构施工措施方面，较少涉及隧道下穿施工引起的桩基承载能力损失研究，尚缺乏较为直观的承载力损失分析方法与评判指标.其次，目前盾构侧穿桩基研究较多，然而盾构桩底下穿施工对桩基影响较大，但桩底下穿施工研究较少.最后，现在盾构施工对桩基影响的数值模拟研究大都直接采用商业数值软件中内置的桩土接触模型，即理想弹塑性或者刚塑性模型，在卸载阶段剪应力与相对位移之间的关系与加载段相同，这与隧道开挖过程中桩土接触卸载特征不同，应采用能够考虑卸载过程的桩土接触模型来模拟这一过程.

因此，针对盾构桩底下穿施工情况展开研究，分析其对桩基承载性能的影响.桩土接触模型采用能够考虑卸载过程的双曲线荷载传递函数模型，在ABAQUS环境中进行编译实现，并验证其可靠性.提出明确的桩基承载力计算方法；分析隧道开挖引起桩基位移和受力变化；对盾构施工控制水平、桩基初始承载水平和桩底与隧道顶部距离3个影响因素进行分析.

1 考虑卸载过程双曲线荷载传递函数

1.1 考虑卸载过程的双曲线荷载传递函数介绍

Zhang等[9]在土-结构动力相互作用(SSI)循环剪切试验结果[10-11]提出的双曲线解析计算模型基础上，提出了考虑受隧道开挖影响以及桩土界面滑移特性的荷载传递函数.如图1所示为循环SSI试验中剪应力τ与相对位移u的关系，如图2所示为传递函数中剪应力和相对位移之间的双曲线关系，OA和AB为加载段，AC为卸载段，CD为反向加载段，k0为界面的初始剪切刚度，δir为残余界面滑移值，τult(z)为极限侧摩阻力.

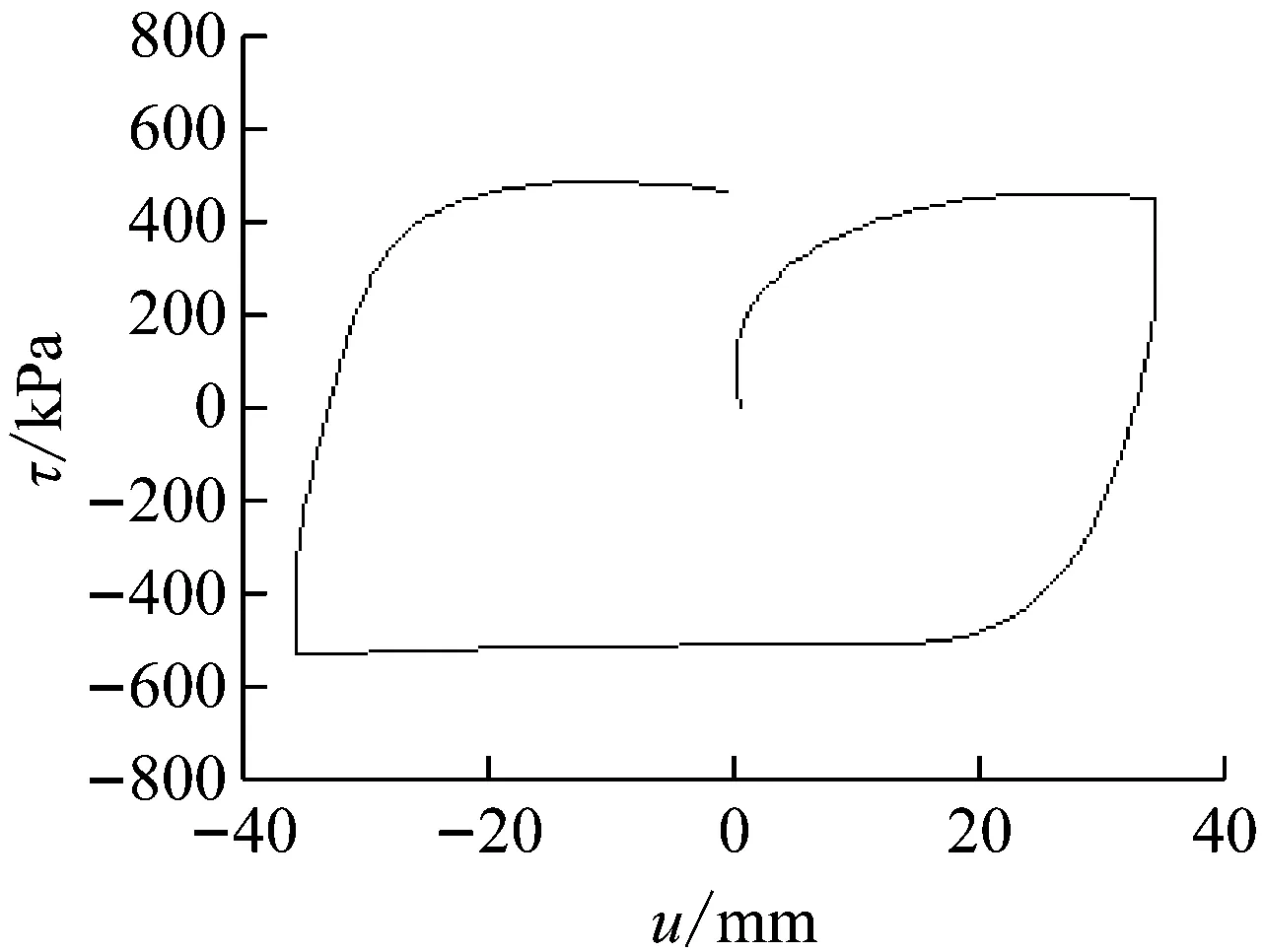
图1 循环SSI试验中剪应力与相对位移的关系

Fig.1RelationshipbetweentheshearstressandtherelativedisplacementintheSSIexperiments

图2 考虑卸载过程的双曲线荷载传递函数

Fig.2Hyperbolicload-transferfunctionconsideringunloadingprocess

式(1)为双曲线关系解析计算式，用于计算侧摩阻力；式(2)计算界面的初始剪切刚度；式(3)计算极限侧摩阻力.

(1)

(2)

τult(z)=ca+σmtanφa

(3)

式中：τ(z)为侧摩阻力；k0为界面的初始剪切刚度；τult(z)为极限侧摩阻力；δ为桩土相对位移；δir为残余界面滑移值；ca为界面黏聚力；σm为侧向压力；φa为界面摩擦角；η为效率系数，是某一时刻桩土界面的剪切力与界面极限剪切力的比值；δ2表示桩土界面的剪切力与界面极限剪切力比值为η时所对应的桩土相对位移值.

1.2 考虑卸载过程的双曲线接触程序编译实现

费康等[12]开始采用古德曼(Goodman)接触模型来模拟接触面上的错动滑裂或者开裂.Goodman认为，接触面在受力之前完全吻合，接触面上剪切力和相对位移之间模拟为非线性弹性关系，接触面的本构关系可用式(4)表示.本文采用Goodman单元非线性特征来实现双曲线的荷载传递函数.将双曲线荷载传递函数关系式(1)对δ求一阶导数，如式(5)所示，可得图2中曲线上任意一点的斜率，然后代入式(4)中.

(4)

(5)

式中：Δτ1、Δτ2分别为方向1、方向2的剪应力；ks1、ks1分别为方向1、方向2的刚度；Δγ1、Δγ2分别为方向1、方向2的相对位移；δn1(n=1,2)分别为方向1、方向2的相对位移；τn1(z)(n=1,2)分别为方向1、方向2的剪切力.

对于上述双曲线接触模型计算每一时步都需要进行受力状态判定.为了便于判断考虑卸载过程的双曲线接触函数上一点的受力状态，将式(5)中的全部δ用摩阻力τ的函数式进行表达，得到根据曲线上任意一点的τ值来确定该点斜率的表达式(6).

(6)

式中：f1(τ) 、f2(τ)为不同加卸载段的刚度.

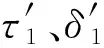
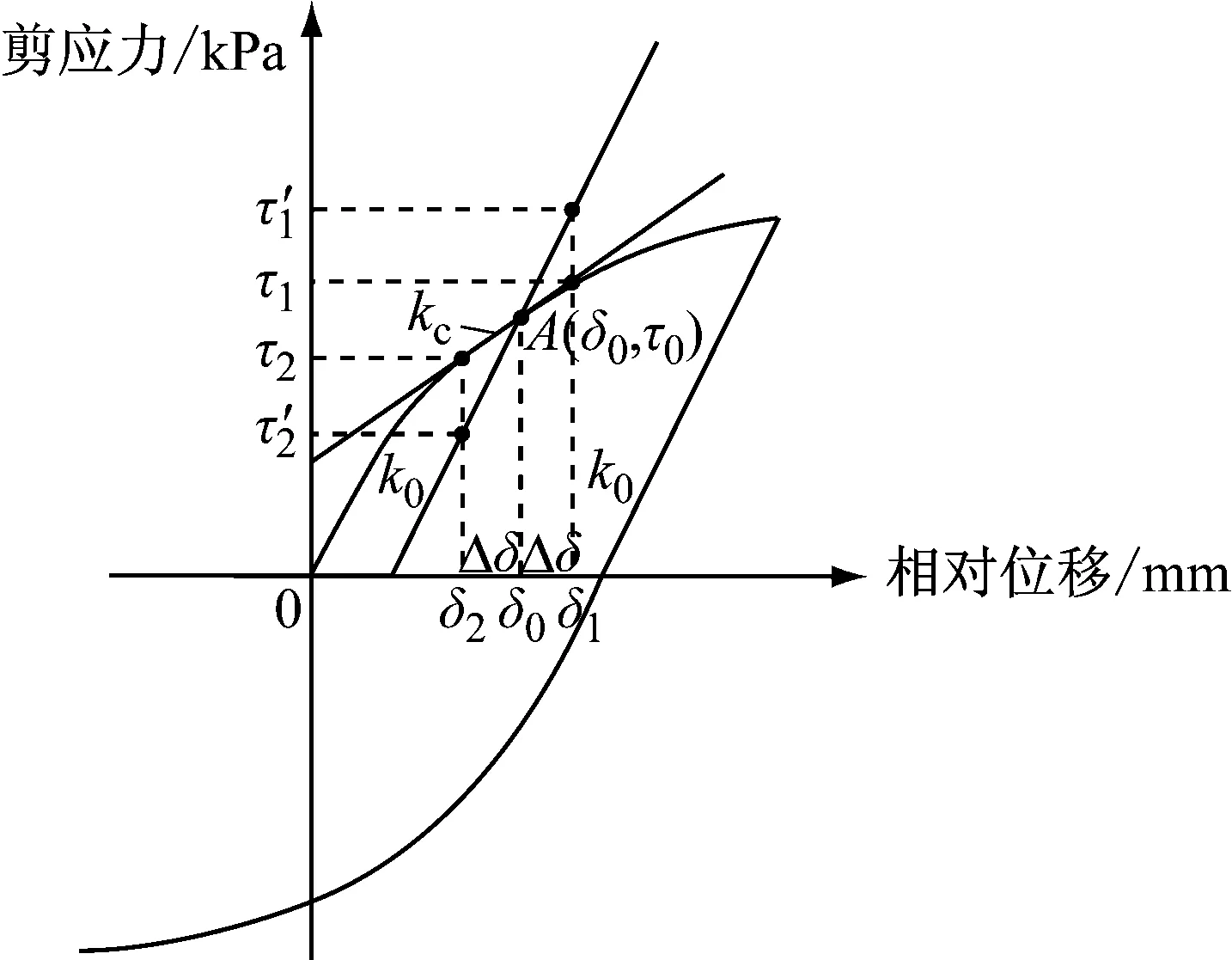
图3 计算点受力状态判定示意

τ1=τ0+kcΔδ

(7)

(8)

(9)

在应力积分算法选择时有多种，如基本增量法、四阶四段龙格-库塔增量法.本文采用计算精度更高的四阶四段龙格-库塔法.采用Fortran语言完成考虑卸载过程的双曲线接触程序编译.

2 双曲线接触程序可靠性验证

2.1 滑块验证

如图4所示，将一尺寸为1.0 m×1.0 m×1.0 m的三维弹性立方体(滑块A)放置在一尺寸为3.0 m×3.0 m×3.0 m的刚体上，刚体完全固定.刚体的弹性模量为1 GPa，泊松比取零，滑块弹性模量10 MPa，泊松比0.4；两滑块间的摩擦系数取0.5，效率系数η取0.8，接触采用考虑卸载过程的双曲线接触程序.整个过程分为4个阶段，第1阶段在滑块A的正上方施加压力P，取值为200 kPa，建立2个部件之间的接触；第2阶段使滑块A沿y轴正向水平移动0.01 m；第3阶段使滑块A沿y轴负方向运动0.01 m回到原点；第4阶段让滑块A从原点开始沿y轴负方向运动0.01 m.得到摩擦力与相对位移的关系如图5所示.

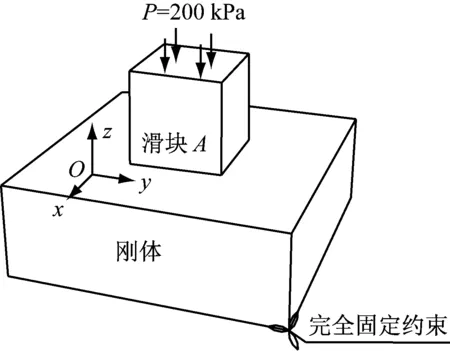
图4 两滑块的相对位置关系

由图5可知，在HE段(0 s～1 s)以及FG段(2 s～3 s)滑块受到的摩擦力以及滑块与固定刚体之间的相对位移呈双曲线关系；在EF段(1 s～2 s)滑块受到的摩擦力以及滑块与固定刚体之间的相对位移呈直线关系.

将根据理论公式计算所得的摩擦力、相对位移的结果也绘制在图5中.看出采用编译的接触模型计算所得摩擦力与相对位移的关系曲线图与理论计算所得的曲线基本重合.由此可知，有限元计算结果与理论公式计算结果一致，说明考虑卸载的双曲线接触模型正确.

图5 摩擦力与相对位移的关系

2.2 模型试验比较验证

为了验证程序的可靠性，采用了Ng等[13]接近桩底正下方单线隧道开挖对既有桩基影响的三维离心试验数据进行比较验证. 隧道开挖通过对开挖部位的土体施加对应体积损失率的位移边界来实现.开挖引起的土体位移模式见图6.土体损失率η与等效土体损失参数g之间的关系如式(10)所示.

(10)

式中：η为土体损失率；g为等效土体损失参数；Sloss为土体损失体积；R为隧道半径.

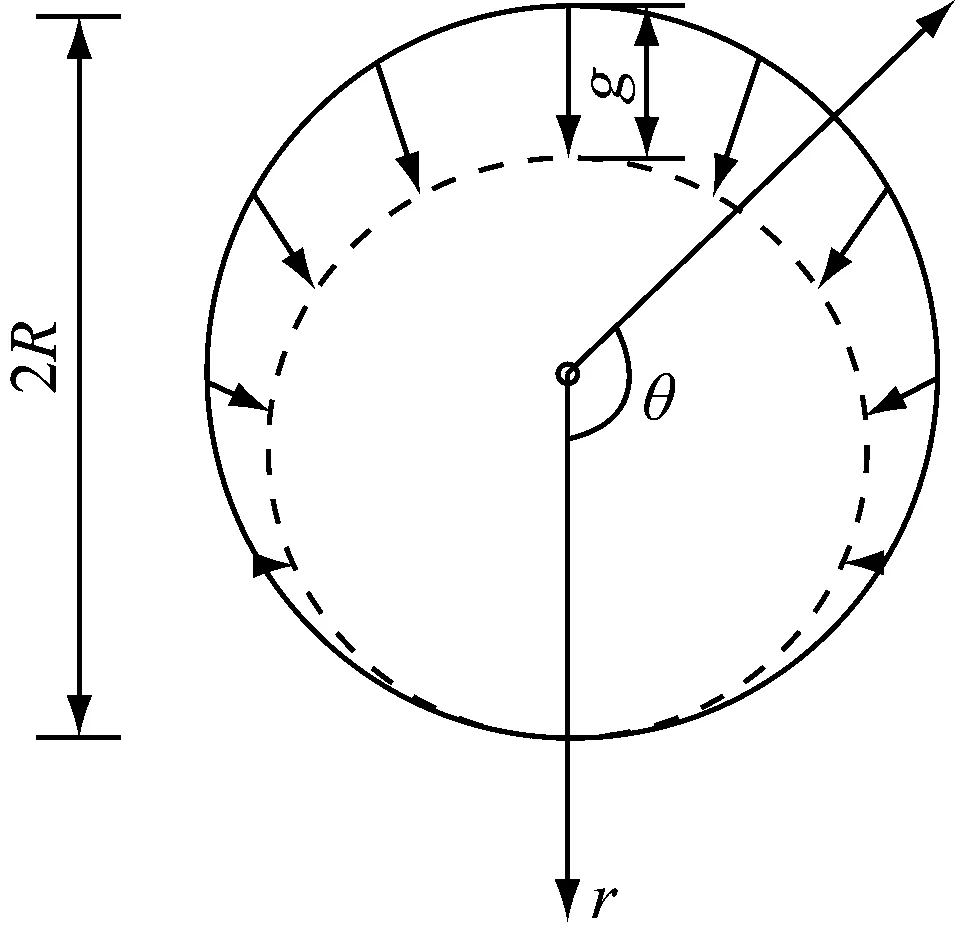
图6 隧道开挖引起的土体位移模式

接触模型验证中参数如表1.土体采用弹塑性模型、摩尔库伦破坏准则；桩体采用线弹性本构模型.盾构开挖引起的体积损失率为1%，体积损失率1%对应的g值为0.031 m.

表1 有限元计算中主要参数

图7为调用程序进行有限元计算得出的隧道开挖前后桩基的轴力分布曲线与离心试验得到的桩基轴力分布曲线对比图，其中D为桩直径.从图中可以看出，隧道开挖前后通过有限元分析所得到的桩基轴力沿深度的变化规律与离心试验得到的轴力分布规律一致且数值接近，说明程序可靠.

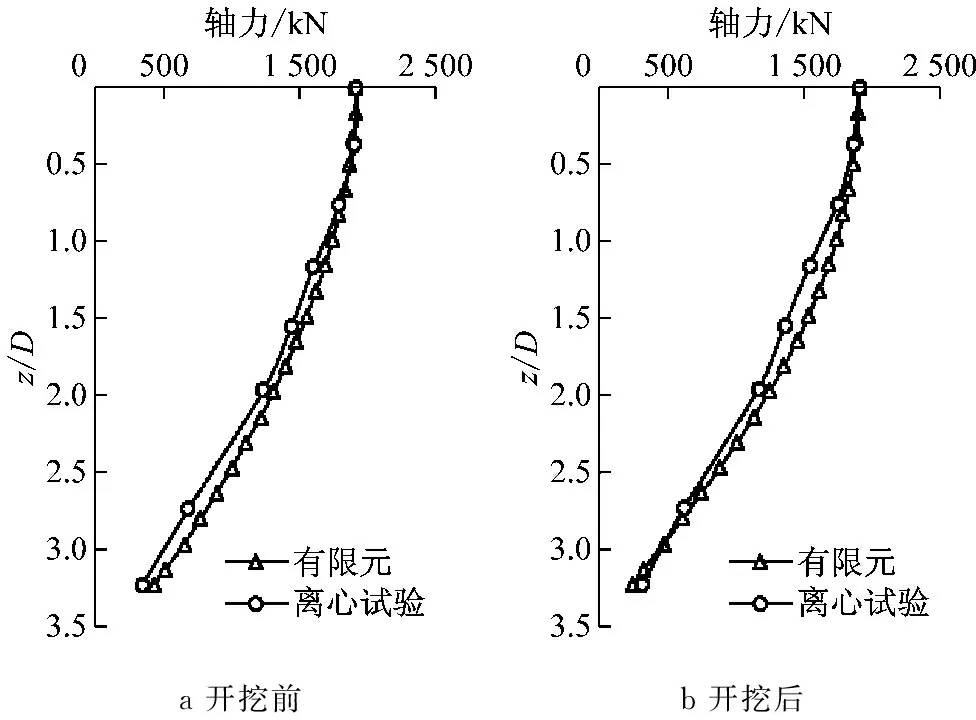
a 开挖前b 开挖后

图7有限元计算轴力与离心试验轴力对比

Fig.7Comparisonofaxialforcebetweenfiniteelementmethodandcentrifugaltest

3 桩基承载力损失计算

3.1 桩基承载力损失表示方法

桩基的承载性能是在保证桩身材料强度的前提下用沉降来描述，由《桩基手册》可知，在单桩静载试验的Q～s曲线中，一般取沉降值40 mm～60 mm对应的荷载值为单桩的极限承载力.我国桥梁和地基基础设计规范等也根据上部结构受力要求，规定了桥墩和房屋桩基允许的沉降值，如 《建筑地基基础设计规范》规定，均匀沉降量不超过50 mm.故取沉降等于50 mm对应的荷载Q为单桩的极限承载力.令Q1为隧道开挖前桩基的极限承载力，Q2为隧道开挖后桩基的极限承载力，隧道开挖具有卸载作用能够引起桩基沉降，那么会导致Q2小于Q1，以式(11)表示极限承载力损失值e.

(11)

3.2 隧道开挖引起的桩基承载曲线变化特征

以杭州地铁1号线某工点作为分析实例.在该工点中，地铁盾构从一办公楼正下方穿过，办公楼桩基采用钻孔灌注桩，共3排，横向间距2 m，纵向间距3 m，前后排3根，中间2根；桩长为8.5 m，桩直径0.5 m，盾构外径为6.2 m.盾构隧道与建筑物桩基的相对位置关系见图8.为消除边界效应的影响，模型的长宽深为60 m×60 m×60 m.桩的直径为0.5 m，桩长8.5 m.土体采用摩尔库伦理想弹塑性模型，土体参数见表2；桩体采用线弹性本构模型，由于在桩长范围内一共有2层土，故桩与土体的接触分两段施加，接触面参数见表3.

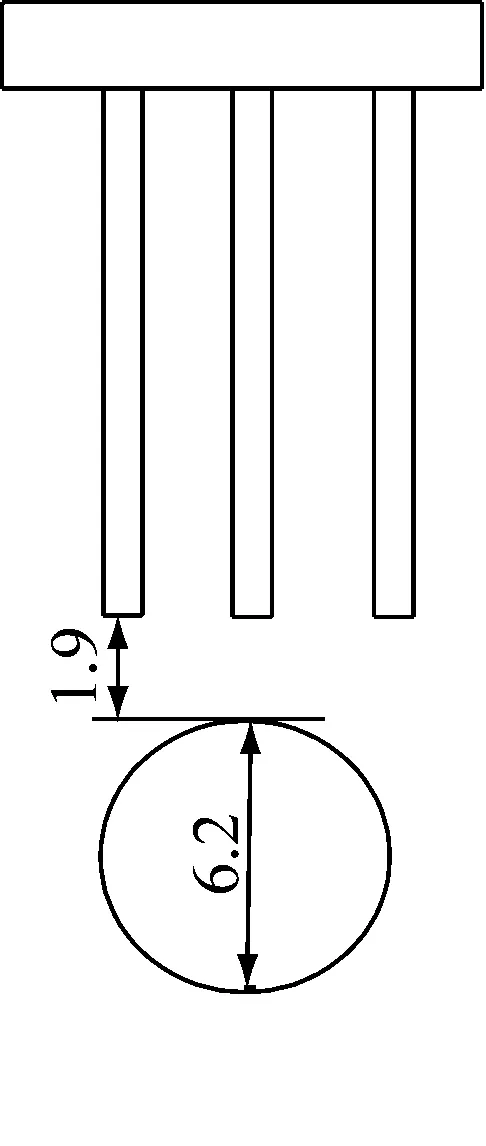
图8 隧道与桩基的横剖面(单位：m)

土层名称重度/(kN·cm-3)压缩模量/MPa黏聚力/kPa内摩擦角/(°)杂填土18.96.410.020.0粉砂、砂质粉土19.011.36.131.0淤泥质粉质土17.23.018.011.0粉质黏土19.56.812.025.0

表3 桩土接触面的参数设置

通过数值模拟得到隧道开挖前和开挖后的桩基Q～s曲线.首先，在没有隧道施工时，进行静载试验，桩顶荷载分8级施加，每一级荷载大小为100 kN，总共加载到800 kN，提取数据得到隧道开挖前的桩基Q～s曲线.然后，在有隧道施工时，先在桩顶施加254 kN的初始工作荷载Q0，模拟桩基已有的受荷状态.第二步进行隧道开挖卸载，通过对开挖部位土体施加对应体积损失率的位移边界来实现，开挖引起的体积损失率取软土地区常用的最大值0.5%.第三步逐级施加桩顶荷载，每一级荷载大小为100 kN，总共加载到800 kN，提取数据得到开挖后的桩基Q～s曲线.

数值模拟结果见图9，O—A—B为隧道开挖前的桩基Q～s曲线，O—A—C—D为隧道开挖后的桩基Q～s曲线.可以看出在A点为在初始工作荷载作用发生的桩基沉降，A点所对应的荷载为桩基初始荷载，OA段为初始荷载导致的桩基沉降.从A点到C点桩基承受荷载没有发生变化，但桩基发生沉降，这是由隧道开挖卸载所引起的，因此以AC段表达隧道开挖过程.图中虚线表示沉降为50 mm，其与OAB曲线的交点所对应的荷载为开挖前的极限承载能力Q1，其与OACD曲线的交点所对应的荷载为开挖后的极限承载能力Q2.因此，图9能充分反应隧道开挖前后桩基承载性能变化情况，可被用来计算隧道开挖引起的桩基承载力损失计算.

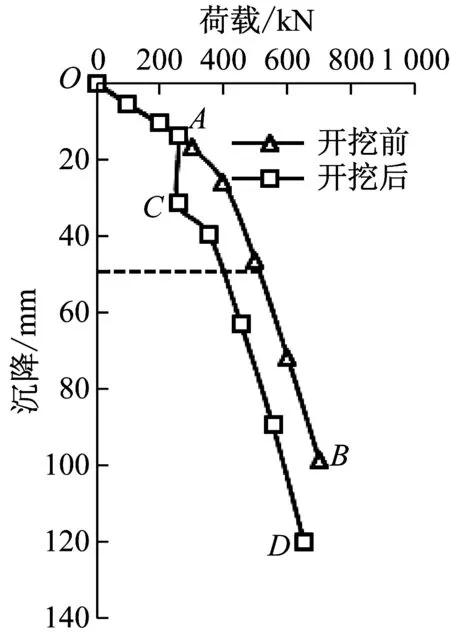
图9 桩基的Q～s曲线

由图9可知，隧道开挖前桩基的极限承载力Q1为508 kN.盾构施工体积损失率控制在0.5%时，隧道开挖后的桩基的极限承载力Q2为400.3 kN.由式(11)计算，得到因隧道开挖导致的桩基承载力损失值为22%.初始工作荷载Q0为254.0 kN，小于开挖后的桩基极限承载力Q2，因此，盾构施工保持该控制水平时，降低了部分桩基承载能力，但不影响桩基础正常使用.

3.3 隧道开挖引起桩基位移和受力变化

针对上述实例，对隧道开挖前后桩基位移和受力变化进行以下分析.以Sp代表桩基的沉降，Ss代表桩周土的沉降，图10所示为开挖前后桩基与桩周土的沉降变化.隧道开挖前后桩基的总沉降分别为8.5 mm、27.8 mm，且桩的总沉降值均大于桩周土的总沉降.

a 开挖前b 开挖后

图10桩基与桩周土体的变形

Fig.10Deformationofpileandsoilaroundpile

图11所示为隧道开挖前以及开挖引起的桩土相对位移和相对位移增量沿深度分布的情况.可知在隧道开挖前以及开挖后各阶段中，相对位移δ(δ=Sp-Ss)均为正值.这意味着在整个桩长范围内，桩的沉降值均比桩周土的沉降值大，若规定侧摩阻力向上为正，则桩受到的均为正摩阻力的作用.但相对位移增量在0～1.05D范围内为正值，则开挖导致该范围侧摩阻力增大；相对位移增量在1.05D～1.40D范围内为负值，该范围内侧摩阻力有所减小.在1.05D处侧摩阻力大小不发生改变.

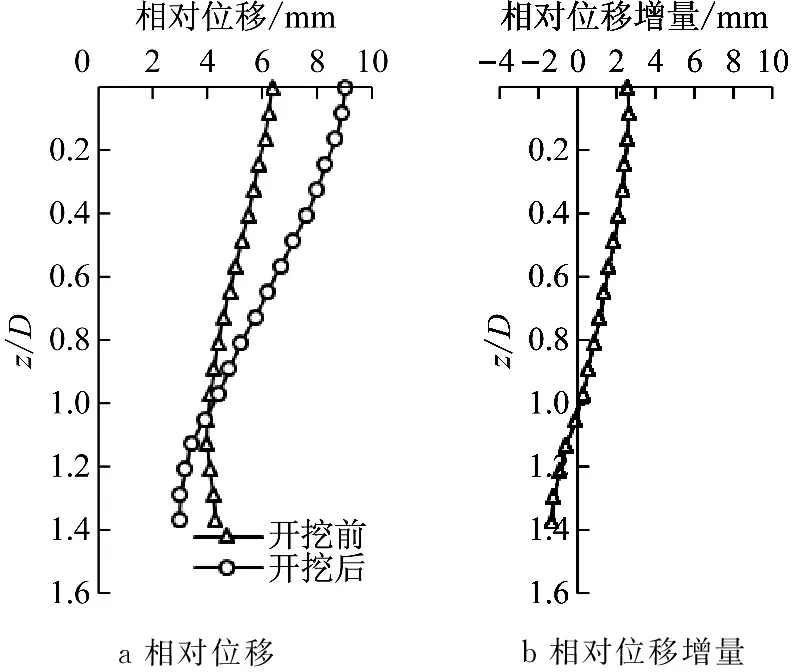
a 相对位移b 相对位移增量

图11桩土相对位移和桩土相对位移增量分布

Fig.11Distributionoftherelativedisplacementandtherelativedisplacementincrementbetweenpileandsoil

如图12a中所示，侧摩阻力变化量与上述观点一致.此外，图12a还表明侧摩阻力分布沿深度先增大后减小.桩基侧摩阻力与桩侧土压力和桩土相对位移的发挥程度均相关.在深度小于1.10D的范围内，桩侧土压力线性增大，桩土相对位移逐渐减小，但桩侧土压力增大对侧摩阻力的影响比较显著，故侧摩阻力表现为逐渐增大；在1.10D～1.40D深度范围内，由于桩体的压缩导致桩土相对位移继续减小，虽然在此深度范围内桩侧土压力也线性增大，但其对侧摩阻力的影响程度小于桩土相对位移减小所产生的影响程度，故侧摩阻力在该范围内逐渐减小.图12b所示为开挖前后桩基轴力沿深度分布图，可以看出隧道开挖后桩基轴力都有所减小.

a 侧摩阻力b 轴力

图12桩基侧摩阻力和轴力分布

Fig.12Distributionoflateralfrictionalresistanceforeonpileandaxialforceinpile

3.4 桩基承载力损失的影响因素分析

盾构隧道桩底施工时造成桩基承载力损失的因素主要有土层力学性质、盾构施工控制水平、桩基初始荷载水平和桩底与隧道顶部距离.土层力学性质直接影响土层提供侧摩阻力和桩端反力的能力，反应到图9桩基Q～s曲线上为直接影响OAB和OACD曲线特征.盾构施工控制水平是对整个盾构施工过程的笼统表述，学术界用地层体积损失率来整体表达盾构施工控制水平，在图9桩基Q～s曲线上为AC段特征，当体积损失率越大时，AC段造成的沉降就越大.桩基初始荷载水平为桩基承载能力已经发挥的程度，在图9桩基Q～s曲线上为反应A点在OB段中所处的位置.桩底与隧道顶部距离越近，隧道开挖卸载造成的桩基沉降越大，在图9桩基Q～s曲线上主要反应在AC段.

由于土层性质过于复杂，桩基所处的持力层、侧摩阻力层和盾构穿越断面地层等不同，对承载力影响的结果都有很大不同，因此对于地层性质的影响常作具体问题具体分析.工程中盾构施工控制水平是重中之重；桩基的初始荷载水平除了影响承载力损失以外，也用于衡量是否具有足够的储备承载力来承受盾构穿越造成的承载力损失；桩底与隧道顶部距离是工程设计时需要解决的关键问题.因此，在上述实例的基础上，对盾构施工控制水平、桩基初始荷载水平和桩底与隧道顶部距离3个因素做规律性分析.

(1)盾构施工控制水平.用体积损失率来表示盾构施工控制水平，通过不同的体积损失率来计算盾构施工控制水平对单桩承载性能的影响.计算结果如图13所示，盾构施工控制水平对桩基的承载性能影响显著，承载力损失值随着体积损失率的增大而增大.当体积损失率增长到1.5%时，桩基的承载力损失值增加到40%.因此，在盾构下穿桩基时应努力提高盾构控制水平.

图13 不同体积损失率下的承载力损失值

(2)初始荷载水平.为了表示桩基在初始情况下的受荷状态，用式(12)来表达桩基的初始荷载水平ζ，Q0为初始桩顶荷载，Q1为隧道开挖前桩基的极限承载力.分别进行ζ为10%、20%、30%、40%、50%的情况下隧道开挖时桩基承载性能影响计算.计算结果如图14所示，桩基的初始荷载水平越大，开挖引起的桩基承载力损失值也越大，即桩基在初始情况下的承载力发挥得就越多，隧道开挖对桩基的承载力影响也更为显著.但是，桩基初始荷载从10%提高到50%时，承载力损失量只是提高了5%.因此，对于初始荷载水平的敏感性要低于盾构施工控制水平，降低体积损失率能够更加有效地降低承载力损失.

(12)

(3)桩底与隧道顶部距离.h为桩底与隧道顶部距离，进行h为1D～6D(增长梯度为0.5D)的隧道开挖计算.除h发生改变以外，其他参数保持不变，体积损失率为0.5%，桩及土体的尺寸、桩土的物理力学参数设置同上.图15为桩基承载力损失值与不同h/D的关系图.由图可知，承载力损失值随着h/D的增大而曲线减小.当h/D增加到6时，隧道开挖引起的桩基承载力损失值减小到近10%.据此可认为，当h/D≥6以后，隧道开挖对桩基的影响已较小.

图14 不同初始承载水平下的承载力损失值

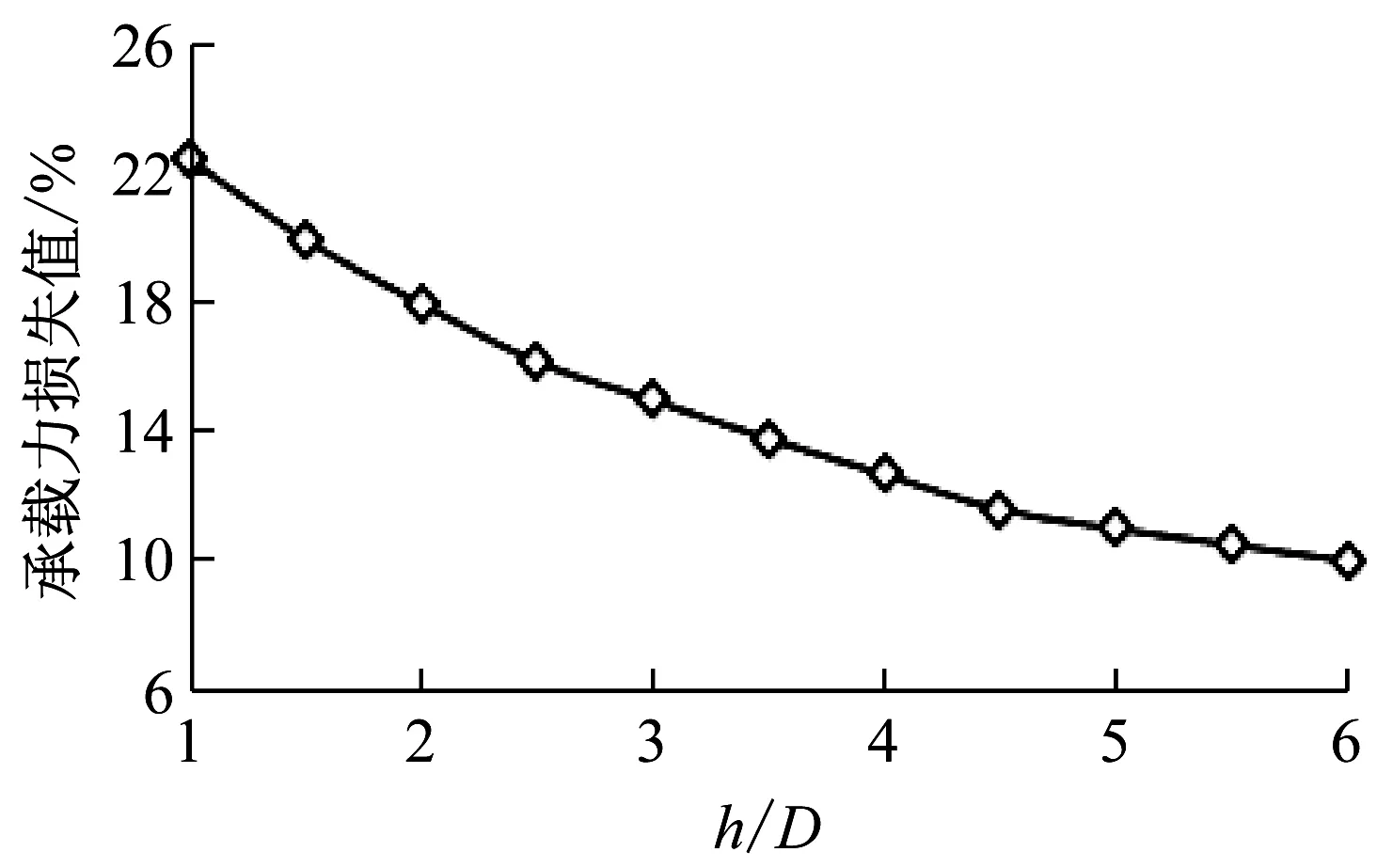
图15 不同桩底与隧道顶部距离下的承载力损失值

Fig.15Lossofpilecapacityatdifferentdistancebetweenpilebottomandtheroofofthetunnel

4 结论

(1)提出一种盾构桩底施工桩基承载能力损失计算方法.先实现考虑卸载过程的双曲线荷载传递函数编译，然后利用该桩土接触模型得到隧道开挖前和开挖后的Q～s曲线；取s=50 mm时对应的荷载为桩基极限承载能力，采用桩基极限承载力损失百分比作为隧道开挖对桩基承载性能影响的评价指标.并结合实例，分析了桩基承载曲线变化特征、桩体内力变化规律和承载力损失影响因素.

(2)在实例中，隧道开挖前桩基的极限承载力Q1为508.0 kN.盾构施工体积损失率控制在0.5%时，隧道开挖后的桩基的极限承载力Q2为400.3 kN.隧道开挖导致的桩基承载力损失值为22%.初始工作荷载Q0为254.0 kN，因此，盾构施工保持该控制水平时降低了部分桩基承载能力，但不影响桩基础正常使用.隧道开挖后，桩体中存在一点侧摩阻力不变，在该点上部桩体侧摩阻力增大，在该点下部桩体侧摩阻力有所减小.

(3)盾构隧道桩底施工时桩基承载力损失的影响因素主要有土层力学性质、盾构施工控制水平、桩基初始荷载水平和桩底与隧道顶部距离.承载力损失值随着体积损失率的增大而增大；桩基的初始荷载水平越大，承载力损失值也越大；桩底与隧道顶部的距离越大，桩基承载力损失值越小；承载力损失对盾构施工控制水平更加敏感，降低体积损失率能够更加有效地降低承载力损失.