现代智能型全站仪不整平不对中测量的可行性分析

顾玄龙，刘成龙，郭 伟

(1. 西南交通大学地球科学与环境工程学院，四川 成都 611756；2. 西南交通大学高速铁路运营安全空间信息技术国家地方联合工程实验室，四川 成都 611756)

自从高速铁路测量技术引入我国后，全站仪自由测站、自由设站[1]等测量新方法的出现打破了传统测量的方式，上述两种测量新方法无需对全站仪进行对中，避免了对中误差，但需要对其进行精确整平，这样多少都会带来整平误差。在一些实际工作中，全站仪是无法精确整平的，或整平时无法和目标点通视[2]，或整平测量影响效率，因此研究智能型全站仪不整平(此时不对中)测量技术，可以解决一些工程实际问题，提高工作效率。

文献[2—5]也研究了全站仪的不整平测量，但都直接认为全站仪整平与不整平测量时的站心坐标系可以通过公共点进行相互转换，并未探究全站仪在整平测量与不整平测量时，存在哪些不变的量，也未探究全站仪在不整平测量时的坐标计算模型。且文献[2]提到全站仪不整平测量的坐标转换精度要比整平条件下差一些。本文从全站仪整平与不整平测量时的观测量及不整平测量的三维坐标计算模型进行研究，探究全站仪不整平测量时如何建立坐标系；测量过程中观测量发生了怎样的变化；不整平测量得到的观测值其精度是否有保障。基于上述问题，本文分析了全站仪在不整平不对中测量时的相关技术问题，并通过试验数据验证了其可行性。本文研究为实现智能型全站仪不整平测量的高精度坐标转换，应用于高速铁路的轨道精调过程提供一种新的测量方法。

1 全站仪整平与不整平测量时的坐标系及其坐标计算模型

常规全站仪整平状态坐标测量时的坐标系是站心坐标系，坐标系的原点O就是全站仪三轴的中心，水平度盘的零方向为Northing(X轴方向)，全站仪的竖轴方向为Elevation(Z轴方向)，与Easting(Y轴方向)构成左手坐标系O-XYZ，这样的站心坐标系XOY面为水平面，Z轴方向为铅垂方向。全站仪整平时坐标测量的坐标系如图1中O-XYZ所示。

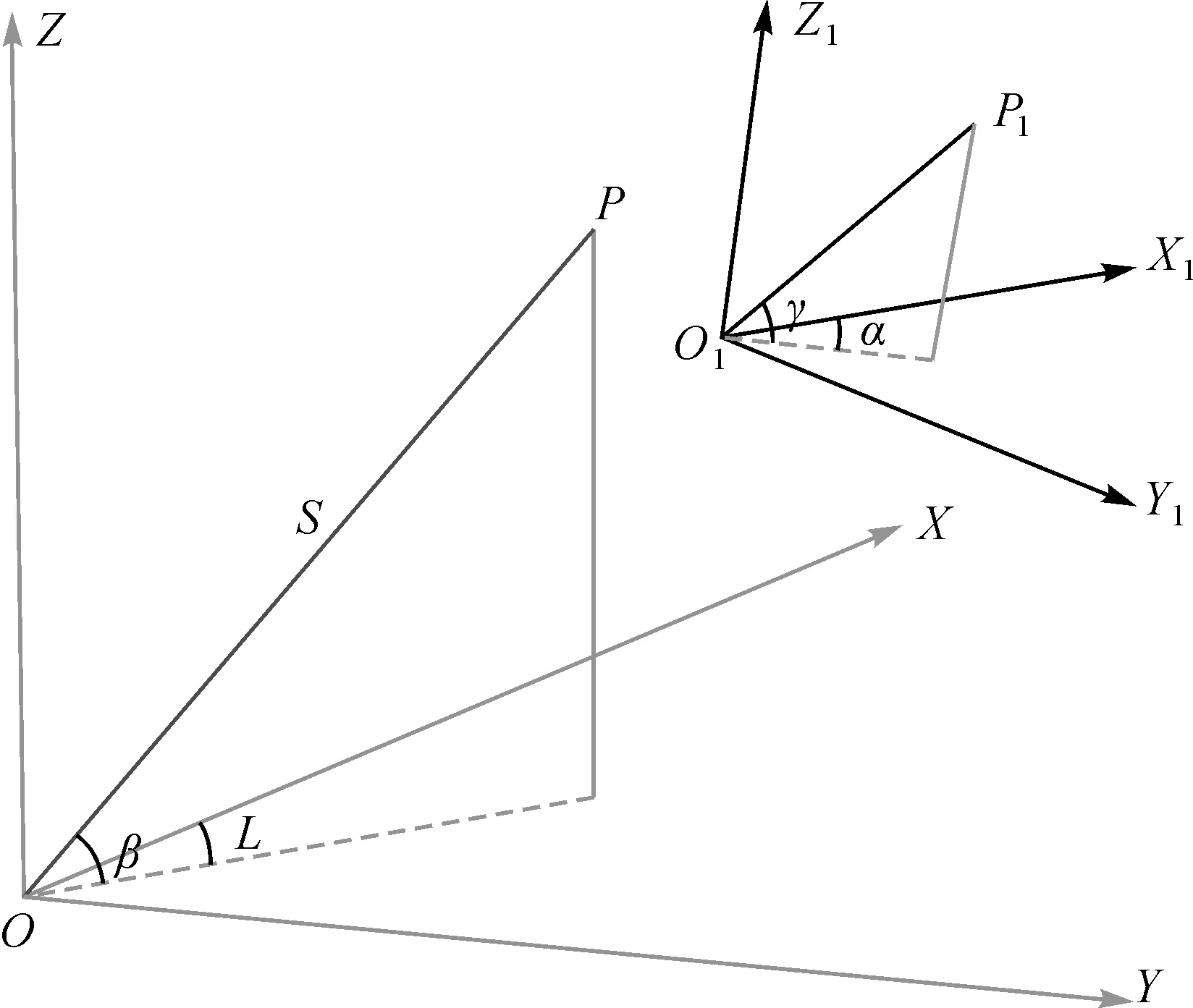
图1 全站仪整平与不整平测量状态下的坐标系示意图

全站仪在整平状态下，通过其测量的水平角L、垂直角β和测站点到目标点的斜距S计算目标点的坐标，其三维坐标计算模型为[3]

(1)

式中，xj(ΔNij)、yj(ΔEij)和zj(ΔUij)为全站仪整平时测量的目标点三维坐标；Lij、βij和Sij分别为全站仪此时采集的三维观测值水平角、竖直角和斜距。

全站仪在不整平状态下进行三维坐标测量时，需要关闭全站仪的自动补偿功能，此时其三维坐标系中的XOY面不再是水平面，Z轴也不再是铅垂线方向，因此全站仪不整平时测量，从全站仪水平和竖直度盘上得到的观测值不能再称为水平角和垂直角。文献[4—5]及本文的试验证明，在关闭了全站仪的自动补偿功能之后，不整平状态下的全站仪仍然可以进行测量，并得到测站到目标点的三维观测值(斜距、空间角α和γ)或目标点的三维坐标，此时的三维坐标是全站仪不整平状态下空间站心坐标系中的坐标。但是，对全站仪不整平测量技术的研究，存在如下几个关键问题需要探讨：①不整平状态下的全站仪，其站心坐标系统是如何建立的？②不整平状态下的全站仪，其站心坐标原点O在测量过程中是否发生变化？③不整平状态下的全站仪，测量得到的三维观测值和坐标是否可靠？④整平状态下全站仪的站心坐标系和不整平状态下全站仪的站心坐标系之间是否可以通过公共点相互转换？

通过研究认为，全站仪在由整平到不整平的状态变化过程中，其三维站心坐标系在空间上发生了旋转和平移，且全站仪在不整平测量的过程中，仪器中心(站心坐标系的原点O)始终不发生变化，即在不整平测量过程中同一测站其站心三维坐标系始终保持同一个姿态[6]。由于全站仪在不整平状态下，从其度盘上采集的观测值不能称为水平角和竖直角，这两个观测值是相对于此时的三维坐标系下得到，是空间角的概念，为了方便表述，分别称其为空间角α(由原水平度盘上得到)和空间角γ(由原竖直度盘上得到)，如图1中的O1-X1Y1Z1所示[7-8]。文献[9—11]和本文研究表明，全站仪无论在小倾斜角还是大倾斜角不整平状态下测量目标点三维坐标的数学计算模型均为

(2)

2 全站仪不整平测量的可行性试验

为了研究全站仪不整平测量的相关技术，本文设计进行了如下的试验。本次试验采用TCA2003全站仪，首先将全站仪安置在场地中间的Z1处，并设置温度、气压和棱镜常数等参数；然后，将4个带有精密基座的棱镜精确整平合理置放在试验场地中的A、B、C、D处，构成良好的观测网形，如图2所示。

在全站仪精确整平和补偿器打开的状态下，利用其自动照准功能采用全圆方向距离观测法[12]对上述4个目标点测量一测回，上下半个测回均归零，记录目标点A、B、C、D的三维坐标。然后，全站仪脚架在原地不动，关闭补偿器，仅通过旋动基座上脚螺旋使全站仪处于不整平的状态，此时目标点A、B、C、D保持不动，且无需转动棱镜方向，称为小倾斜角不整平测量试验，按照上述相同的测量方法观测2个测回，依次记录目标点A、B、C、D的三维坐标，如图2所示，此时的仪器中心发生了小的变化，设为测站Z2。最后，将全站仪移动至距离测站Z15 m左右的地方，仍然关闭补偿器，全站仪仍处于不整平的状态，目标点A、B、C、D保持不动，且无需转动棱镜方向，称为大倾斜角不整平测量试验，按照同样的测量方法观测两个测回，依次记录目标点A、B、C、D的三维坐标，如图2所示，此时的测站中心为Z3。

通过上述3次测量试验均可以得到目标点A、B、C、D的三维坐标，为探究全站仪整平与不整平测量结果之间是否存在某种联系，以全站仪盘左测量的三维坐标为例，计算统计了目标点A、B、C、D之间的平面距离、角度和空间距离的差异情况。

2.1 目标点间的平面距离比较

分别比较分析了整平与小倾斜角不整平测量、整平与大倾斜角不整平测量、小倾斜角与大倾斜角不整平测量时6条目标点之间的平面距离较差，见表1。

图2 全站仪整平与不整平测量实验场地布置图

类型变化区间/mm不同区间所占比例/(%)[0,1]mm(1,10]mm(10,258.64]mm整平与小倾斜角不整平测量的平面距离差值20.11～258.640 0 100整平与大倾斜角不整平测量的平面距离差值0.08～38.0116.716.766.6小倾斜角与大倾斜角不整平测量的平面距离差值17.56～220.6400100

从表1可以看出，全站仪在3种不同状态下测量，计算出的6条目标点间的平面距离差值最大为258 mm，且差值绝大部分在10 mm以上。因此，得出结论：全站仪整平与不整平测量时，目标点间的平面距离差别很大，因此不整平状态下测量的X、Y坐标不是平面坐标。

2.2 目标点之间的角度比较

分别比较了整平与小倾斜角不整平测量、整平与大倾斜角不整平测量、小倾斜角与大倾斜角不整平3种情况测量下，由目标点A、B、C、D构成的三角形△ABC、△ADC、△ABD、△BCD共12个内角角度的较差，见表2。

表2 不同测量状态下目标点间的角度较差统计

从表2中可以看出，全站仪在3种不同状态下测量，目标点间构成的12个三角形内角角度差最大达到了4′54″，且绝大部分在20″以上。因此，得出结论：全站仪在整平与不整平测量时，目标点之间构成的三角形内角角度发生变化，这也说明不整平状态下全站仪测量的X、Y坐标不再是平面坐标，因此不整平状态得到的三角形内角不是平面角。

2.3 目标点间的空间距离比较

分别比较了整平与小倾斜角不整平测量、整平与大倾斜角不整平测量、小倾斜角与大倾斜角不整平测量下，6条目标点之间的空间距离较差，见表3。

从表3中可以看出，全站仪在3种不同状态下测量，计算出的6条目标点间的空间距离差值均在1 mm以下，最大较差为0.88 mm。因此，得出结论：全站仪整平与不整平测量时，目标点间的空间距离没有发生变化，这说明不整平状态下全站仪测量的空间坐标是准确的。

表3 不同测量状态下目标点间的空间距离较差统计

由于全站仪在不整平(小倾斜角和大倾斜角)测量时各观测了两个测回，那么目标点之间的空间距离在不整平状态下测量的两个测回间是否存在较大差异？同测回盘左盘右测量的目标点的空间距离是否存在较大差异？如若存在较大差异，那么全站仪在不整平状态下，无法实现多测回的观测，半盘位观测的目标点坐标也不可靠，这样就无法运用在高速铁路的全站仪半盘位自由设站测量[13]技术中。现分别将小倾斜角和大倾斜角不整平测量的第一个测回盘左盘右中解算出的目标点之间的空间距离取均值与第二测回对应的均值、大倾斜角不整平测量时同测回盘左盘右得到的目标点空间距离进行了比较分析，比较结果见表4。

表4 不整平状态下测回间和测回内目标点间的空间距离较差情况统计

从表4中看出，全站仪不整平状态测量时，无论是小倾斜角还是大倾斜角，不同测回间目标点间的空间距离均值较差均在1 mm以下。大倾斜角不整平测量时同测回盘左盘右间目标点间空间距离较差绝大部分在1 mm之下，最大较差为1.09 mm。因此，得到结论：全站仪不整平测量时，不同测回间和同一测回盘左盘右间目标点间的空间距离均值不发生变化，这说明不同测回和同一测回半盘位测量得到的目标点空间三维坐标均是高精度和可靠的。

3 全站仪不整平测量时的三维坐标计算模型验证试验

本次试验采用另一台徕卡超高精度全站仪TS60，场地和目标点布置仍然如图2 所示。试验时，关闭全站仪的补偿器，各目标点保持不动，在全站仪小倾斜角和大倾斜角不整平状态下，设全站仪仪器中心坐标为(0,0,0)，将测站至目标点A的方向作为起始方向并置全站仪原“水平度盘”读数为0，在全站仪不整平的状态下采用全圆方向距离观测法对各目标点依次观测并记录三维观测值空间角α、空间角γ和斜距，同时记录各目标点三维坐标。

全站仪在小倾斜角和大倾斜角不整平状态下的三维坐标计算模型为式(2)，根据全站仪观测的三维观测值计算了各个观测点的三维坐标，并与全站仪测量及显示的三维坐标进行比较，计算和比较结果见表5—表8，表中的观测值和实测坐标为盘左盘右的均值。

由表5—表8可以看出，全站仪在小倾斜角和大倾斜角不整平状态下，全站仪显示的实测坐标和由式(2)计算的坐标差值很小，均在1 mm以下，因此式(2)即为全站仪在不整平状态下的三维坐标计算模型。说明全站仪无论在小倾斜角，还是在大倾斜角不整平状态下测量的过程中，全站仪上显示的坐标是站心三维坐标系中的坐标，且假定站心的坐标为(0,0,0)。

4 结 论

经过上文对全站仪的不整平测量试验与相关研究，得到了以下结论：

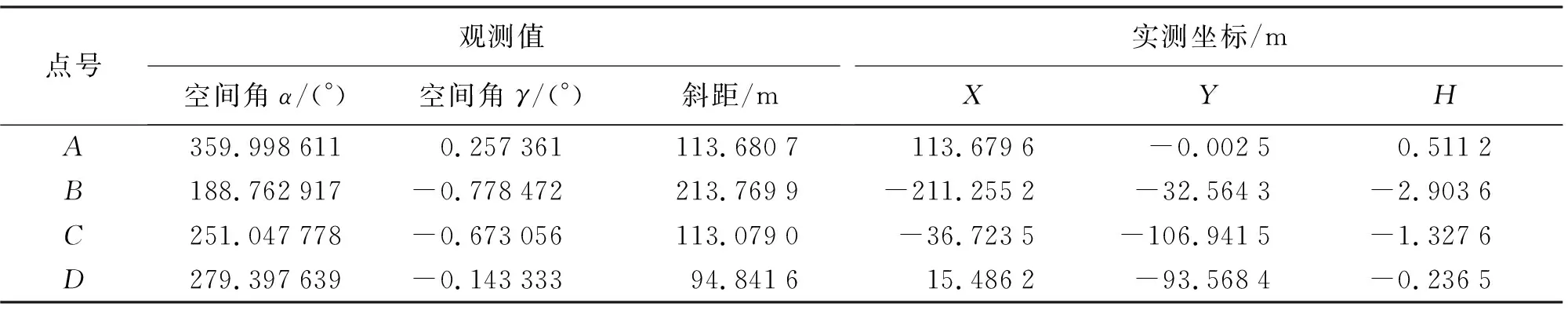
表5 全站仪小倾斜角度不整平状态下显示的实测坐标

表6 全站仪小倾斜角度不整平状态下显示的计算坐标差值

表7 全站仪大倾斜角不整平状态下显示的实测坐标

表8 全站仪大倾斜角不整平状态下显示的计算坐标差值

(1) 现代智能型全站仪可以在不整平和不对中的情况下进行高精度的三维观测值测量，此时的三维观测值分别为空间角α、空间角γ和斜距，与整平状态下的三维观测值水平角和竖直角截然不同(斜距除外)。

(2) 现代智能型全站仪可以在不整平和不对中的情况下进行高精度的三维坐标测量，但是这样的三维坐标是任意站心三维坐标系中的坐标，无法在工程中直接使用，必须通过公共点进行高精度的三维坐标转换到工程坐标系中后才能在工程中使用，而如何进行高精度的三维坐标转换，是笔者后续研究的内容。

(3) 现代智能型全站仪不整平和不对中的测量新技术，可以在一些特定的条件下大幅度地提高测量效率。