一种机载LiDAR点云缺失数据的填补方法

王丽英，夏玉红，徐 艳，赵元丁

(1. 辽宁工程技术大学,辽宁 阜新 123000； 2. 北京金景科技有限公司，北京 100094)

机载激光雷达(light detection and ranging，LiDAR)技术可快速获取具有三维坐标和一定属性(强度等)的海量、不规则空间分布三维点云[1]，为三维地理空间信息获取提供了全新的技术手段。独特的优势使得点云数据需求量随之剧增。然而点云中常存在局部数据缺失，产生缺失数据的原因包括：条带不重叠；系统无法记录数据；完全透射或吸收性地物导致无反射回波；遮挡。缺失数据在点云中呈现出空洞现象(如图1所示)，因而也被称作数据空洞。其存在导致相应区域的地物细节不能体现，从而影响数据的完整性，进而对后续点云数据的处理、分析和应用产生消极影响。其中，前两类缺失数据可以通过补飞的方式重新获取；然而，后两类缺失数据则是无法避免的。因此，需辨识并填补各类数据缺失。

图1 数据空洞示例(不同灰度代表高程不同)

经典的数据空洞填补方法包括最低点填补、邻近填补及基于地形的填补。最低点填补[2-6]提取数据空洞的外边界中高程最低值作为数据缺失区域的高程；邻近填补[7-10]将与待填补点距离最小的数据点的高程作为待填补点的高程；基于地形的填充方法[11-15]针对点云数据栅格化过程中出现的空白区域，对其边界进行一维形态学滤波得到其边界各点地形高，利用边界点构建不规则三角网进行地形内插填充。上述3种方法均利用数据空洞的外边界点的高程信息填补数据空洞，未考虑数据空洞的影响区域。只有根据数据空洞边界轮廓线确定其影响区域的大小，进而用影响区域内的点云构造逼近的连续曲面才能实现填补数据与周围数据的光顺连接。因而，影响区域的确定是数据空洞填补的最重要因素。另外，针对同一数据空洞，采用不同的空间插值方法填补空洞的效率及精度均不同。因而选择最优的空间插值方法是数据空洞填补的另一重要因素。针对上述两个因素，本文提出一种数据空洞辨识及填补方法。该方法基于空洞轮廓凸包等距扩大原理确定数据空洞的有效影响区域；利用影响区域内的数据点集，针对空洞的高程特性，研究不同空间插值算法补偿空洞的精度，进而选择最优的空间插值方法并补偿空洞。

1 缺失数据填补原理

算法流程如图2所示。首先，依据空洞几何特征及其空间分布构建数据空洞图，检测空洞的存在；其次，对其进行连通区域标记，将数据空洞分割为单一数据空洞；然后，针对大面积的单个数据空洞，提取其边界轮廓并将其等距扩大获得数据空洞的有效影响区域；最后，利用影响区域内点云，借助最优空间插值算法完成缺失数据填补。

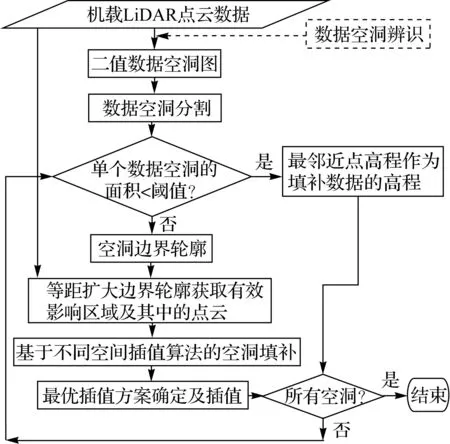
图2 数据空洞填补流程

1.1 数据空洞辨识

用数据空洞图表征数据空洞的存在。数据空洞图为一幅二值图像，可用具有一定分辨率的二维格网(格网边长取平均点间距)覆盖整个场景目标的xy平面，并定位其中空的格网单元获得，如图3所示。其中，空洞为黑色像素，像素值为0；非空洞为白色像素，像素值为1。

图3 数据空洞

1.2 数据空洞分割

对数据空洞图中的0值像素进行8连通区域标记，将数据空洞图分割并标记为单一数据空洞。进而统计各个空洞的面积，若其面积小于给定阈值Ta，则取该空洞的最邻近点的高程作为该空洞内各个数据点的高程；否则，需进入下一步确定该空洞的有效影响区域，并利用影响区域内点云，借助最优空间插值算法完成缺失数据填补。

1.3 数据空洞的有效影响区域确定

在数据空洞的填补处理中，为了保证填补数据与周围点云实现最佳融合，填补数据需利用数据空洞的周围一定区域内点云数据，运用空间插值理论确定。其中，周围数据的范围及空间插值方法直接影响空洞填补的效率及精度。本文首先基于数据空洞的轮廓向外等距扩大确定空洞的有效影响区域，进而用影响区域内的点云构造逼近的连续曲面以实现填补数据与周围数据的最佳融合，详细方案如下：

(1) 提取数据空洞的外边界轮廓，搜寻位于其上的数据点作为其外边界轮廓点。

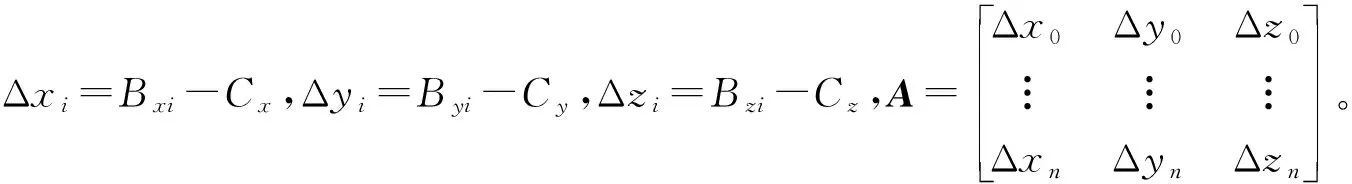
(3) 计算Bi到平面α的距离方差E和Bi投影到平面α所得边界轮廓曲线(记作K)上的数据点的曲率均值k′。

(1)

式中，di为Bi到α的距离；X0为距离di的均值；m为K中的数据点数量；κi为数据点i处的曲线曲率。

(4) 根据E和k′将K向外等距得到扩展的边界轮廓(记作K′，K′=cK)，向外等距的距离c即最佳影响区域。其中，c=δE+εk′,δ+ε=1。如图4所示。

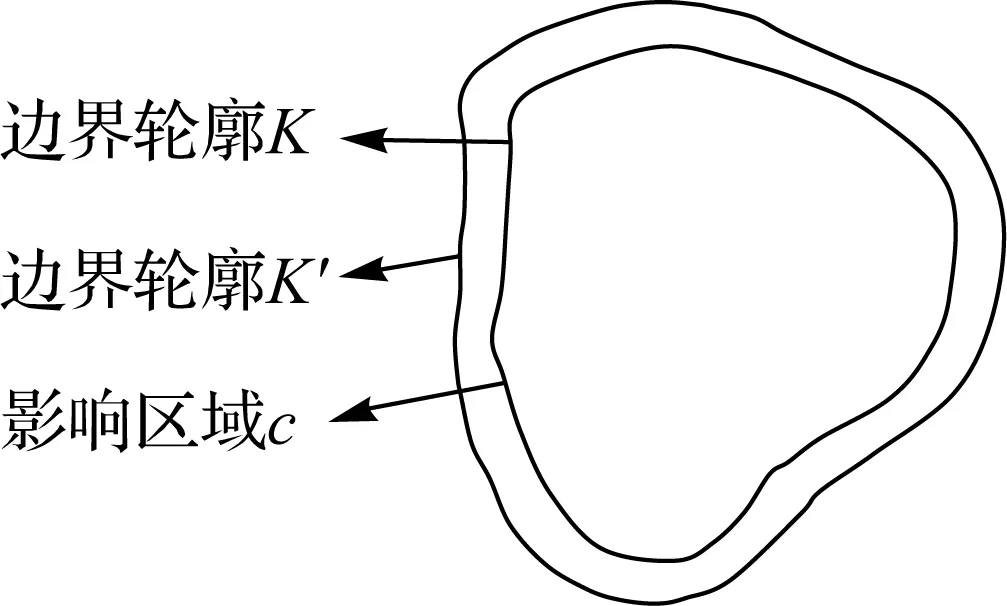
图4 影响区域

1.4 最优空间插值方案确定及数据空洞填补

针对同一数据空洞，利用影响区域内的数据点集，研究不同空间插值算法填补空洞的精度，进而选择最优的空间插值方法并填补空洞。

2 试验数据

采用剪切自国际摄影测量与遥感协会(International Society for Photogrammetry and Remote Sensing，ISPRS)第三工作组(http:∥www.itc.nl/isprswg III-3/filtertest/)提供的包含不同的数据空洞类型的实测点云数据，如图5所示。其中，FSite5如图1所示。数据由Optech ALTM系统获取，图5、图1中各个数据的激光脚点平均点密度分别约为0.75、0.14个/m2，回波次数为2。

图5 试验数据

3 试 验

本文算法在CPU Core(TM)i5-2400 3.10 GHz、内存4 GB、Windows 7旗舰版系统上使用Matlab 7.11.0平台编程实现。

3.1 影响区域的有效性

试验旨在验证提出的数据空洞影响区域的确定方案的有效性。从CSite4中剪切一块点云数据，如图5(c)中区域所示。上述剪切数据可用作数据空洞的标准数据。试验针对剪切后区域(即数据空洞)。首先利用本文提出的方案确定数据空洞的影响区域；然后利用某一空间插值算法(反距离插值)填补空洞内数据点(填补的数据点的平面坐标和标准数据中数据点的平面坐标一一对应，但各个数据点的高程不同)；最后对比填补结果和标准数据，计算空洞填补结果的中误差(见式(1))，见表1中第1列所示。同时，为了验证上述影响区域方案的有效性，将影响区域等距扩大1倍、2倍，或缩小50%、75%，得到不同的影响区域(如图6所示)，并基于上述影响区域结果计算空洞填补结果中误差，见表1中第2～5列。

(2)

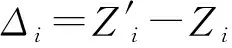
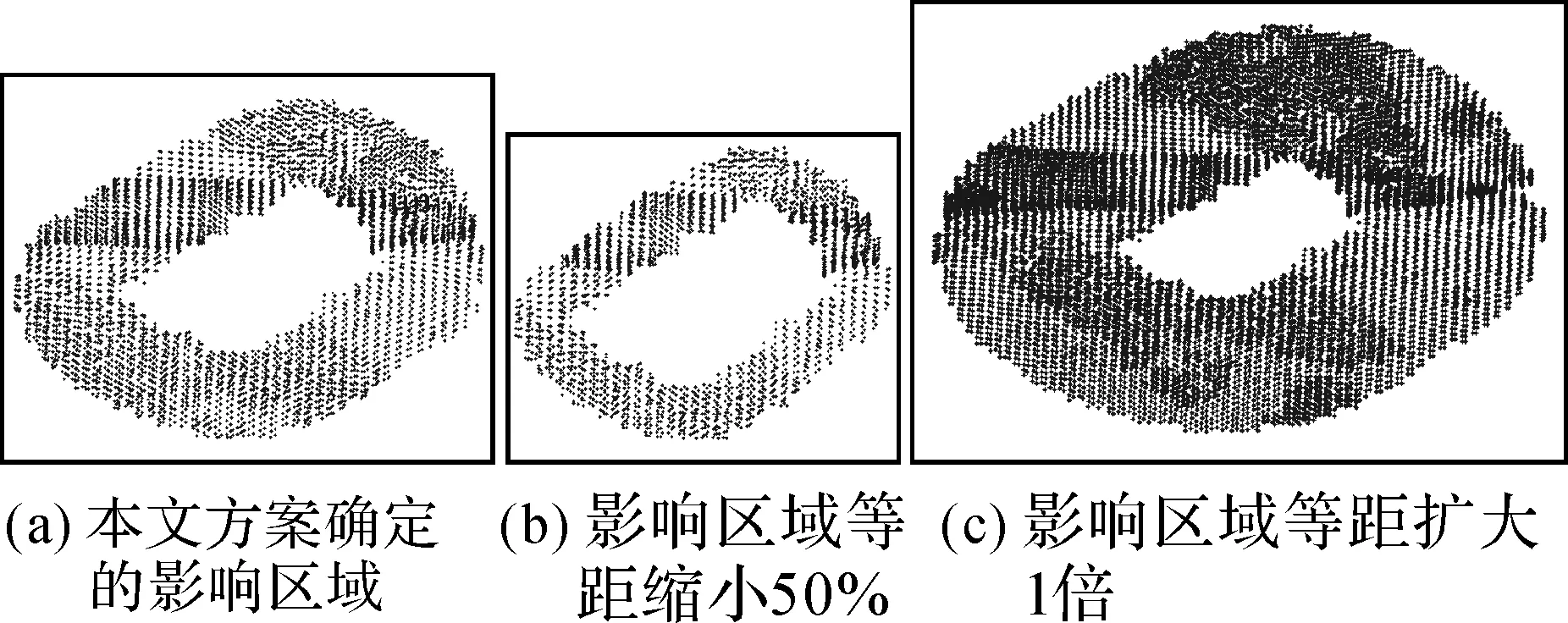
图6 不同的影响区域及其内的点云

本文确定的影响区域影响区域等距缩小50%影响区域等距缩小75%影响区域等距扩大1倍影响区域等距扩大2倍0.0641.7310.9780.1450.132

由表1可知，本文的影响区域确定方案对应的空洞填补结果的中误差仅为0.064。在相同条件下，对比其他影响区域，本文的影响区域确定方案对应的空洞填补结果的中误差最小，从而验证本文提出的数据空洞的影响区域方案的有效性。

3.2 不同数据空洞类型的最优空间插值方法确定

对于不同的数据空洞类型，基于数据空洞的影响区域内的数据点，分别采用经典的克里金插值、线性插值、最临近插值和反距离插值等空间插值方法对数据空洞进行填补，研究不同空间插值算法填补的数据空洞的精度，进而选择最优的空间插值方法填补空洞。其中，填补结果的精度评价采用了交叉验证的方法(由于没有数据空洞区域的标准数据，无法直接对比)，即首先填补数据空洞，然后利用填补数据反向插值影响区域内的激光点的高程，进而对比插值结果和影响区域内已知数据，并采用中误差指标进行定量评价。

3.2.1 无反射回波类型的空洞的最优填补方案确定

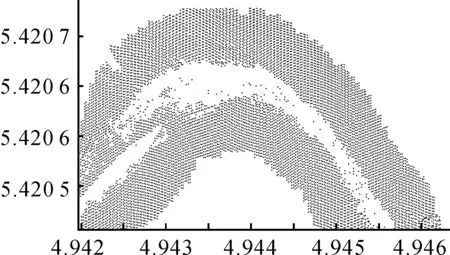
图7 有效影响区域及其内点云顶视图

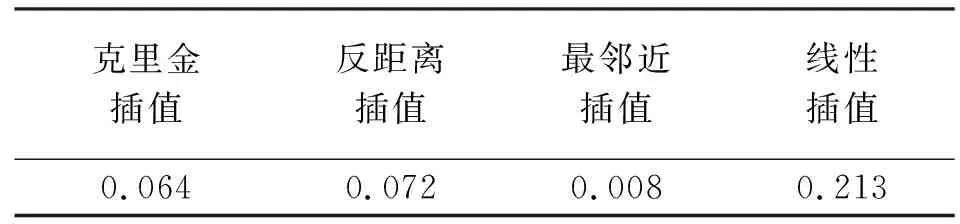
克里金插值反距离插值最邻近插值线性插值0.0640.0720.0080.213

由表2可知，从中误差指标来看，最邻近插值对应的填补结果中误差最小，其为无反射回波类型的数据空洞填补的最优空间插值方案。基于最邻近插值的空洞填补结果如图8所示。

3.2.2 目标遮挡类型的空洞的最优填补方案确定

试验数据如图5(b)所示。由于目标遮挡类的数据空洞的影响区域内必然包含部分高大目标点云，而基于影响区域内高大目标点云填补数据空洞必然造成较大误差。因此，可首先统计影响区域内点云的高程特性，若出现两个正态分布，则仅取影响区域内高程值小于谷底高程的点云填补数据空洞。基于不同的空间插值算法影响区域内的点云填补数据空洞，并采用交叉验证的方法进行精度评价，见表3。

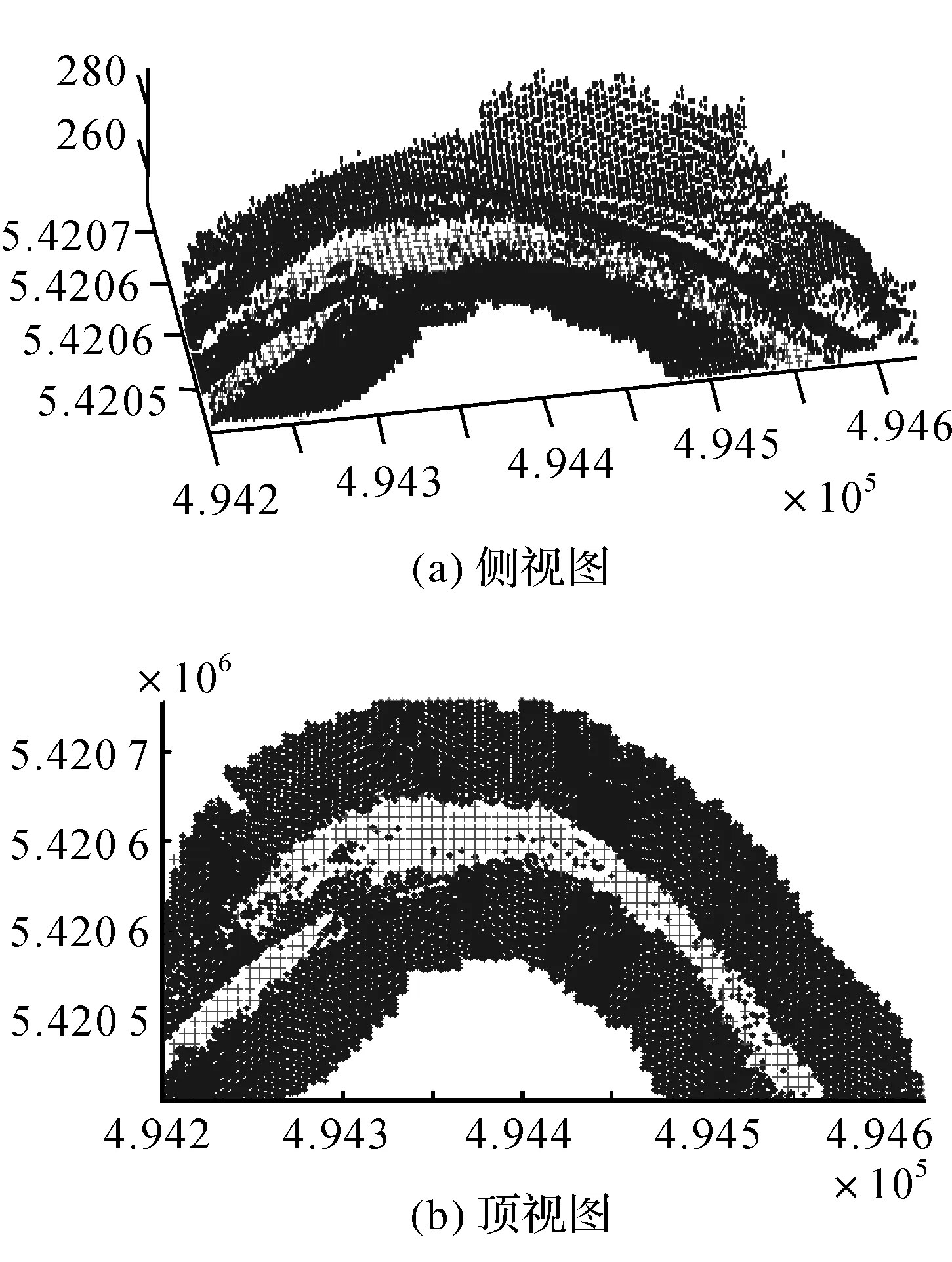
图8 最邻近插值的填补结果

克里金插值反距离插值最邻近插值线性插值0.0980.1310.0410.439

由表3可知，从中误差指标来看，最邻近插值对应的填补结果中误差最小，其为目标遮挡类型的数据空洞填补的最优空间插值方案。

3.2.3 航带不重叠类型的空洞的最优填补方案确定

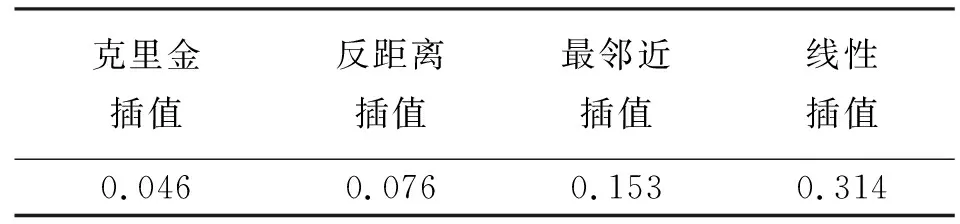
表4 不同空间插值算法对应的填补结果中误差

由表4可知，从平均绝对误差指标来看，克里金插值对应的填补结果中误差最小。上述结果表明：克里金插值方法为目标遮挡类型的数据空洞填补的最优空间插值方案。

4 结 语

本文提出了一种缺失数据填补方法。该方法利用二值数据空洞图检测缺失数据的存在，进而利用连通区域标记算法将数据空洞图分割为单个数据空洞，然后对大面积的数据空洞的外边界轮廓进行等距扩大获得数据空洞的有效影响区域，最后研究不同的缺失数据类型的最优空间插值方案，并基于影响区域内的点云，利用最优空间插值方案对不同类型的缺失数据进行填补。创新工作主要围绕数据空洞的有效影响区域确定和不同数据空洞类型的最优空间插值方法两个方面。试验基于ISPRS提供的包含了不同类型的空洞的点云数据测试了影响区域的有效性、不同类型的缺失数据的最优空间插值方案，从而验证了提出方法的有效性。本文研究的不足之处在于：对于不同的缺失数据类型的最优空间插值方案的研究仅采用了4种经典的空间插值算法，而未考虑其他空间插值算法；填补结果不但与数据空洞类型有关，还与数据空洞的范围大小密切相关，但本文未考虑空洞范围对填补结果的影响。在以后的研究中，应考虑上述两方面及填补效率的问题。