优化的证据冲突融合方法

陈元超

(中国空空导弹研究院，河南 洛阳 471009)

0 引言

证据理论由Dempster于1967年研究上下概率问题时首先提出，后由其学生Shafer将信任函数概念引入而正式形成[1]。证据理论作为一种多源信息融合方法，有着坚实的数学基础，是不确定性推理方法的一种[2-3]。证据理论通过对不完整性、不确定性问题的数学建模，为多传感器信息融合提供了一个很好的方向。

证据理论由于其优越的特性被应用到军事信息融合系统中，然而由于复杂的自然环境和人为干扰，某些探测传感器得到的信息被干扰而与其它传感器产生冲突。对于高度冲突的证据信息，经典的证据理论融合会产生有悖常理的结果，很难正确对目标进行识别。对于这一问题，很多学者进行了研究，提出了多种解决方法[4-9]，但在某种程度上存在精度低、收敛效率低的问题。

针对证据冲突的融合问题，本文结合Jousselme距离[10]和Pignistic概率距离[11]的优点提出了优化的证据冲突融合方法。

1 证据理论及其存在的问题

1.1 证据理论合成原理

在同一识别框架Θ下，设来自两个证据源的基本概率分配函数m1和m2，对于∀A⊆Θ，命题A的信任函数通过证据体m1和m2的正交和得到，其合成规则为[12]：

m(A)=m1(A)⊕m2(A)=

(1)

式(1)中，A1,A2为命题A的子命题；k为经典冲突系数，表达式为：

(2)

而(1-k)-1被称为归一化因子。对于在识别框架Θ下，如果对于命题A存在多个证据体m1,m2,…,mn时，它们合成过程可以通过两个证据体时的前两项的情况进行推导，合成规则如式(3)：

m2(A2)×…×mn(An),A≠Φ

(3)

冲突系数k表达式为：

(4)

它用来表示证据间的冲突情况。

1.2 证据冲突问题

证据理论在实际应用中，对于来自多源的证据体，当证据体之间存在明显的冲突时，经典证据理论所融合的结果往往得出错误的结果。对于证据冲突问题，现举一例进行详细说明。

例1 对于一个假定的识别框架Θ=(A,B,C)，来自两个证据源的证据体，

证据体m1：

m1[A]=0.99,m1[B]=0.01,m1[C]=0；

证据体m2：

m2[A]=0,m2[B]=0.01,m2[C]=0.99。

从证据体m1可以看出对目标A的支持最大，对其他两个目标的支持概率明显小于目标A；而证据体m2的概率分布情况和证据体m1明显不同，证据体m2支持的目标是C。可以看出两个证据源得到的证据体是高度矛盾的，根据证据理论的合成规则对两个证据体进行合成，得到如下的概率分布结果,合成证据体m：m[A]=0,m[B]=1,m[C]=0。

从合成结果可以看出，对于两个高冲突的证据体，如果以经典的证据理论合成规则进行融合，会得出有悖常理的结果。原证据体m1和m2分别支持目标A和C，而合成结果却完全支持本来概率较低目

标B，这明显不符合实际情况。这一算例也体现了证据理论合成规则的另一个问题，一票否决问题，即当证据体中某一命题被彻底否定时，该命题的融合结果也被一票否决，如例1中证据体m1否决目标A，融合结果A被否决。另外，根据证据理论合成规则的合成公式(1)可知，当冲突系数k趋近于1时，即两个证据体完全冲突时，合成公式分母趋于零，证据理论合成规则失效。

2 优化的证据冲突融合方法

2.1 总体思路

本文应用证据理论主要是针对军工系统的目标识别领域，对系统得到的多源信息，如果证据体间存在冲突，可以认为信息源存在干扰，是证据源本身的问题。所以采用的第二大类思想对证据理论进行优化，优化证据理论方法的思想流程如图1所示。

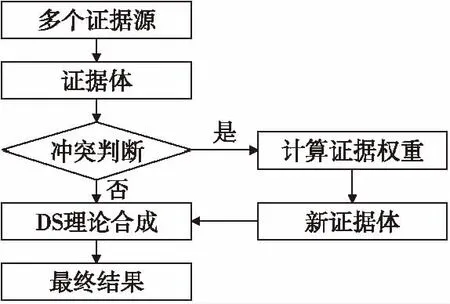
图1 证据理论优化流程图Fig.1 Flow chart of optimized evidence theory

从图1可以看出，首先从多个证据源得到信息，通过一定的方法计算各个信息源的证据体；其次计算各个证据体之间的冲突性，如果两个证据体间存在冲突，通过一定方法计算各证据体的权重，然后得到新的证据体，否则直接合成；最后将新的证据体通过经典证据理论合成规则得到最终结果。

2.2 证据体的测量

对证据体进行测量来分配证据体间的权重，通常认为两个证据体间的距离越大，证据间的相似度越小，它们冲突性就越高。为了全面反映证据间的冲突情况，引入两种距离函数来测量证据体。

2001年Jousselme等学者将向量空间引入证据理论[10]，提出了一种距离函数来度量两个证据间的相似情况，当距离函数值越大，表明两个证据间的相似度越小。因此可以将Jousselme距离函数作为判断证据间冲突情况的一个测量指标。Jousselme距离函数定义如下：

假定Θ为一包含N个两两不同的命题的完备的识别框架,m1和m2是在识别框架上的两个概率分配函数，即两个证据源的证据体，则m1和m2的Jousselme距离的具体的计算方法如式(5)所示。

(5)

式(5)中，m为证据体m的向量表示，‖m‖2=〈m,m〉为向量的内积，而内积具体算法如式(6)所示：

(6)

Pignistic概率距离，于2006年由学者Liu引入证据理论中[11]。Pignistic概率距离描述证据体间对于不同焦元支持程度的最大差别， Pignistic概率距离越大, 表明两个证据体之间冲突越大。Pignistic概率距离具体定义如下：

假定Θ为一个的完备的识别框架，m为识别框架下的概率分配函数，Pignistic概率函数为：

1.4.1 检查因素：为了明确病变的部位、病因、病理解剖和病理生理等诊断要素，除了问诊和体检，还需要做一系列的检查，但各种检查都存在敏感性和特异性的问题，也就是说这些检查客观上不是百分之百正确无误的。至于正常值则是一个参考范围，必然有一部分患者会纳入正常，也会有一部分正常人归为异常。此外，检查结果有测定前误差、测定误差和测定后误差。上述因素都会从客观上干扰我们的思维，影响疾病的诊断。病理检查的结果应当是特异性最高的实验检查，也是临床医师最为重视的报告。但病理检查的各个环节都会影响结果，如标本的采集、固定和保存，切片染色以及阅片等等。

(7)

式(7)中，|A|为焦元A中包含的元素个数，BetPm的含义为各个子命题在识别框架上的概率分布情况，即对子事件的支持程度。

两个证据体mi和mj之间的Pignistic概率距离定义为Pignistic函数差的最大值：

dP(mi,mj)=max(|BetPmi(A)-BetPmj(A)|)

(8)

2.3 新证据体计算

对某一系统，从n个信息源得到n个证据体，当中间存在证据体与其他证据体冲突时，不可以按经典合成规则进行合成，需要将证据体进行调整。首先对于n个证据体，计算两两证据体之间的距离dij(Jousselme距离函数dJ和Pignistic概率距离dP)，得到一个n×n的距离矩阵D：

(9)

通常认为，两个证据体间的距离越大，相似度就越小，冲突性就越高。因为距离的范围为0到1，所以定义两个证据体之间的相似度sij为：

sij=1-dij,i,j=1,2,…,n

(10)

得到距离矩阵D后，计算两两证据体之间的相似度sij，可以得到相似度矩阵S：

(11)

接下来将相似度矩阵中每一行除自身的相似度之外的所有元素的和定义为每个证据体mi的支持度zi：

(12)

证据体mi的支持度zi反映了mi被其他证据体所支持的程度，从式(12)可以看出，它是相似度的函数。如果一个证据体与其他证据体比较相似，它们间相似度较高，则证据体的支持度数值越大； 如果一个证据体与其他证据体相似度较低，则证据体的支持度数值越小。将每个证据体的支持度归一化处理后定义为可信度，它反映的是一个证据体的可信程度。可以认为，一个证据体被其他证据支持的程度越高，该证据体就越可信，它的权值就越大；如果一个证据体不被其他证据体所支持，则认为该证据的可信较低，权值就小。求得证据体mi的支持度zi之后，可以计算得到证据体mi的权值qi：

(13)

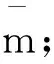
m(A)=q1×m1(A)+q2×m2(A)+…+

(14)

通过Jousselme距离dJ和Pignistic概率距离dP分别将n个证据体处理得到两个新的证据体，将它们进行证据理论合成之后，用合成结果与得到新证据体dJ和dP的均值合成n-2次，得到最终结果。

3 仿真验证

为了验证优化冲突证据融合方法的可行性与优越性，通过2个算例来仿真验证。

例2 对于一个假定的识别框架Θ=(A,B,C)，A,B,C为要识别的目标，来自同一探测系统的三个传感器的探测结果为：

探测器1m1：

m1[A]=0.7,m1[B]=0.1,m1[C]=0.2；

探测器2m2：

m2[A]=0.8,m2[B]=0.1,m2[C]=0.1；

探测器3m3：

m3[A]=0.1,m3[B]=0,m3[C]=0.9。

以概率最大为判别原则，从例2可以看出，探测器1和2识别的目标为A，而证据体探测器3则为C，说明探测器3与探测器1,2的结果是冲突的，因此，应用本文介绍的优化方法，计算Jousselme距离函数下3个证据体的权值qJ=(0.42,0.39,0.19)，继而通过权值排序去除干扰项，得到Jousselme距离函数下新的证据体mJ=(0.706 9,0.094 3,0.199 0)，计算Pignistic概率距离下3个证据体的权值qP=(0.43,0.39,0.18)，同样的处理得到Pignistic概率距离下新的证据体mP=(0.708 4,0.094 6,0.197 0)。有三个探测器的证据体，需要合成两次。第一次为mJ和mP用证据理论合成规则合成，合成之后的结果再和mJ与mP均值合成一次，得到最终的融合结果：m=(0.976 3,0.002 3,0.021 4)。

从最终合成结果可以看出，三个探测器合成之后对目标A的支持度最大，符合实际情况，说明证据理论优化方法在处理冲突证据时是有效的。

例3 对于一个假定的识别框架Θ=(A,B,C)，A,B,C为要识别的目标，来自同一探测系统的5个传感器的探测结果为，

探测器1m1：

m1[A]=0.5,m1[B]=0.2,m1[C]=0.3；

探测器2m2：

m2[A]=0.0,m2[B]=0.9,m2[C]=0.1；

探测器3m3：

m3[A]=0.55,m3[B]=0.1,m3[C]=0.35；

探测器4m4：

m4[A]=0.55,m4[B]=0.1,m4[C]=0.35；

探测器5m5：

m5[A]=0.55,m5[B]=0.1,m5[C]=0.35。

分别用经典D-S证据理论方法、Mruphy合成方法[5]、Jousselme距离方法[6]、Pignistic概率距离方法[7]和本文优化方法对例3中的探测结果进行融合计算，计算结果如表1所示。

从例3题中可以看出，探测器1,3,4和5支持目标A，而探测器2支持目标B，与其他探测器结果冲突，可以认为探测器2受到干扰。通过表1的融合结果可以看出：对于经典D-S证据理论方法，目标A的识别概率一直为0，尽管其他的探测器都是支持目标A的，由于探测器2否决了目标A，最终结果也否决了目标A。Mruphy合成方法克服了经典D-S算法的缺点，从表1可以看出，随着支持目标A的证据体增多，目标A的支持概率也随之增大，如果以概率最大作为识别标准，Mruphy合成方法要在4个证据体融合时才能识别出目标A。Jousselme距离方法和Pignistic概率距离方法也随着证据体的增多，克服了冲突探测器2对目标A的识别的干扰，对目标A的支持概率越来越大，识别目标A的情况越明显，但收敛效率较低。本文新优化方法对冲突证据体做了很好的处理，在探测器2受到干扰时，通过加权处理能快速准确地识别目标A。优化方法考虑了证据体之间的相互关联性，考虑了各个证据体的有效作用，降低了干扰项对最终融合结果的影响，在较少的证据体下就能使融合结果收敛为正确的目标。在多于两个证据体融合的情况下，对目标A的识别概率，本文新优化方法明显高于其他改进方法。

表1 各种方法融合结果对比表Tab.1 Comparison of various methods of fusion results

4 结论

本文提出了优化的证据冲突融合方法。该方法综合Jousselme距离和Pignistic概率距离在证据测量方面的优点,对冲突证据体进行了加权处理，并剔除了干扰项的影响。通过仿真计算和对比分析，结果表明本文所提出的优化的证据冲突融合方法相比于与几种典型改进方法更好地解决了冲突证据体融合时出现的问题，且收敛效率高，提升了融合结果的可靠性和合理性，能准确有效地识别出目标，为军事信息融合系统精准目标识别提供了重要的参考意义。