高超声速飞行器自适应光滑二阶滑模姿态控制

管 萍，张世先

（北京信息科技大学自动化学院，北京，100192）

0 引 言

随着航空航天技术快速发展，临近空间区域利用与发展已成为各发达国家的焦点。高超声速飞行器（Hypersonic Vehicle, HSV）飞行速度马赫数在5以上，飞行环境延伸到临近空间区域，它独有的军事战略战术优势和民用运输发展前景，使高超声速飞行器成为航空航天领域的研究热点，在国际上引起广泛关注[1]。

HSV因高超声速的飞行速度及临近空间复杂的飞行环境，引起了飞行器气动参数剧烈变化；特殊的机身设计结构，使飞行器的姿态模型呈现高度的非线性和强耦合特性[2,3]。因此，如此复杂的控制问题使传统的线性控制方法面临巨大的挑战。

近几年，鲁棒控制、反步控制、智能控制等控制方法被应用于HSV姿态控制系统研究，并取得很大的进展。针对高超声速飞行器姿态控制，一些学者设计了鲁棒自适应控制器、鲁棒自适应反步控制器、基于自组织小波小脑模型关节控制的滑模控制器等[4～6]，仿真计算都显示出较好的控制效果，然而将其复杂算法应用于实际工程中还存在一定困难。终端滑模控制因其简单的设计结构和强鲁棒性特性，且在系统进入滑动模态后，对干扰具有不变性，与普通的滑模控制相比具有更快的收敛速度，近年来被广泛应用于HSV的姿态控制研究中。文献[7]针对HSV六自由度再入姿态模型设计了Terminal 滑模控制器，保证了控制系统在有限时间内趋于稳定，达到指令的稳定、快速跟踪；文献[8]为了消除终端滑模的奇异性，达到更快的收敛速度，提出了一种新型快速Terminal 滑模控制器，并给出了有限时间稳定性证明。然而上述文献在设计滑模趋近律时采用的是传统的等速趋近律及指数趋近律，因为符号函数的引入，使系统状态趋近滑模面时存在抖振以及控制的不连续性。为了解决符号函数引起的问题，许多学者采用边界层方法或者引入饱和函数来代替不连续项，结果是以损失系统的鲁棒性和精确性为代价。文献[9]为消除抖振问题，提出了一种拟连续高阶滑模控制率，但高阶滑模的设计大大增加了控制系统的计算复杂程度。另外有些文献没有考虑HSV的气动参数剧烈变化问题。

本文以光滑二阶滑模控制为基础[10]，综合考虑HSV姿态模型的气动参数变化、抖振处理及有限时间收敛问题，设计了一种基于滑模干扰观测器的自适应光滑二阶滑模控制策略。能够有效消除抖振并使系统实现有限时间姿态跟踪。滑模干扰观测器对气动参数变化引起的模型不确定性进行了精确估计，且自适应方法的引入使得控制器参数能够在线调节，提高了系统的控制精度。基于李雅普诺夫函数对整个闭环系统进行稳定性证明。最后仿真结果验证了文章所提控制控略的有效性和鲁棒性。

1 HSV姿态控制模型

HSV六自由度姿态控制模型由三自由度质心平动方程和绕质心旋转的三自由度转动方程两部分组成。本文研究的HSV面向姿态控制模型基于以下假设：

a）飞行器无动力飞行时，不考虑因燃料损耗的飞行器质量变化；

b）将飞行器视为刚体，不考虑弹性模态的变化。

根据以上假设条件，考虑地球自转对姿态控制的影响，化简得运动学方程和动力学方程[11]。由于临近空间复杂的飞行环境，飞行器气动参数发生剧烈变化，故引入由于气动参数变化而造成的模型不确定性，得到如下仿射非线性数学模型：

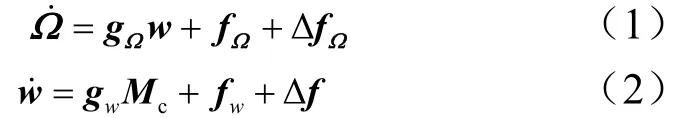
其中，

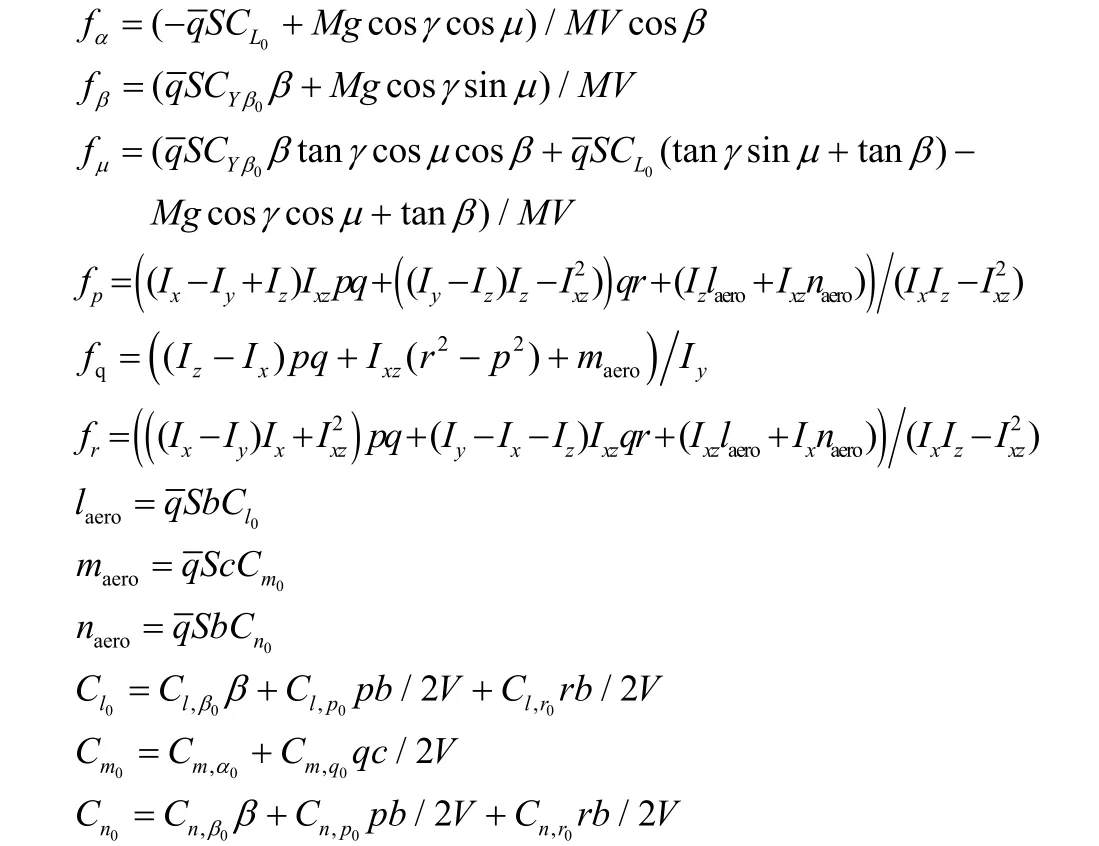
针对具有气动参数剧烈变化的高超声速飞行器，主要控制目标是设计一个合适控制力矩cM使飞行器的实际姿态角Ω能够快速、准确地跟踪期望指令refΩ。分别为

2 基于滑模干扰观测器的光滑二阶滑模控制器设计

根据多时间尺度理论把控制系统分为快、慢双回路；对慢回路子系统进行光滑二阶滑模控制器设计；考虑到气动参数的实时变化对角速率子系统影响较大，对快回路设计一种自适应光滑二阶滑模控制器，使控制参数能够在线调节；同时对快慢回路设计了滑模干扰观测器来精确估计参数变化引起的不确定性部分。慢回路中，cw作为系统的虚拟控制，使Ω跟踪refΩ；在快回路中，cw被看作期望角速率指令，控制器输出控制量cM使角速率w跟踪cw。HSV姿态控制系统结构框图如图1所示。

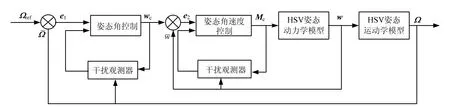
图1 HSV姿态控制系统结构Fig.1 Block Diagram of HSV Attitude Control System

2.1 快回路控制器系统

针对气动参数剧烈变化对姿态角速率子系统影响较大的问题，为提高控制性能，使控制器设计参数能够在线调节，此处控制器设计引入自适应方法。

定义姿态角速率误差为

对式（3）两边求导，并将式（2）代入，得：

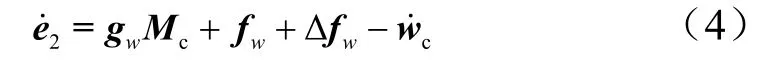
2.1.1 滑模干扰观测器设计

角速度误差子系统中含有不确定性部分Δwf，本文采用超螺旋算法来设计滑模干扰观测器对Δwf进行估计。

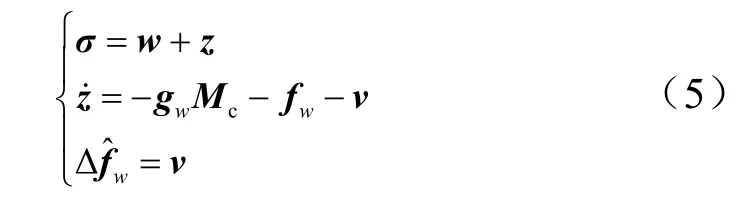
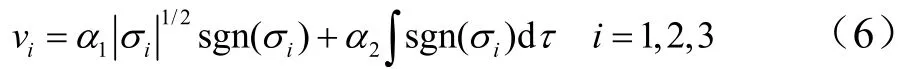
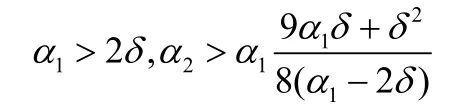
证明：对式（5）求导，并将式（2）代入得：

将式（6）代入式（7）得：

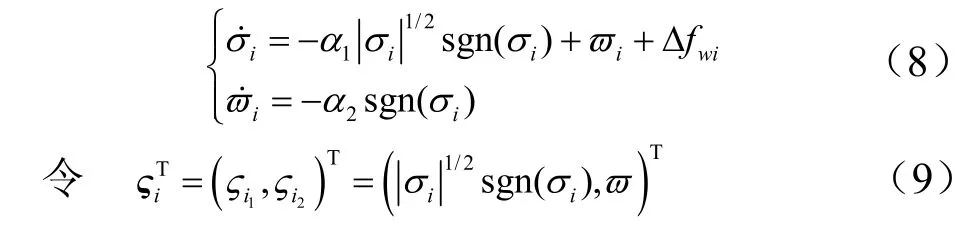
由式（8）、式（9）变换形式如下：

取Lyapunov函数为

对式（11）求时间导数，并把式（10）代入得：

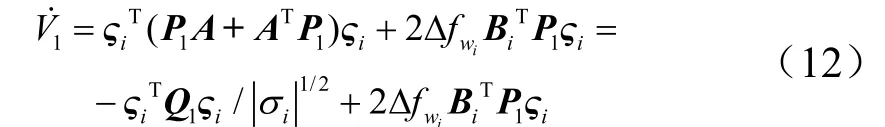
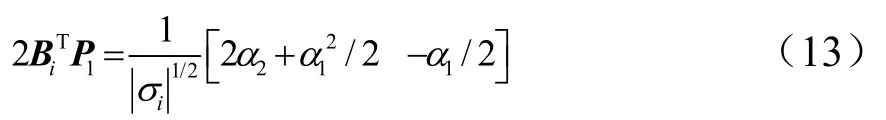
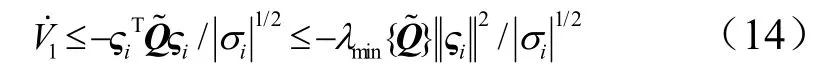
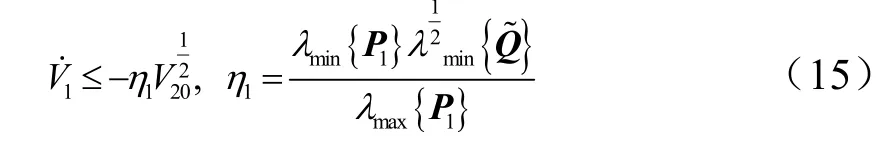
2.1.2 控制器设计

取自适应光滑二阶滑模趋近律为

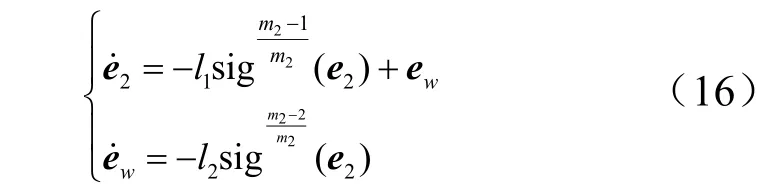
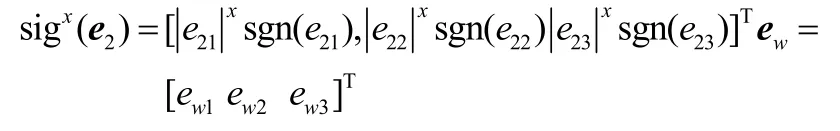
将式（4）和式（16）合并，再结合 2.1.1节干扰观测器设计形式，得到如下自适应光滑二阶滑模控制律，能够使系统（2）有限时间稳定：

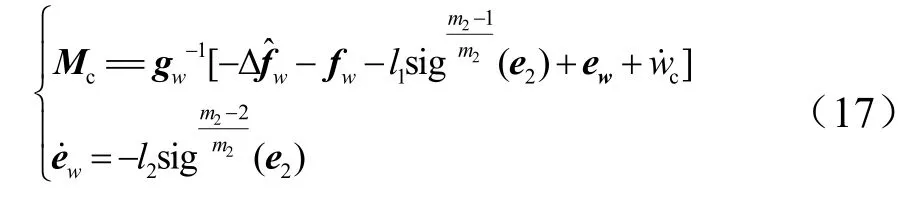
其中，

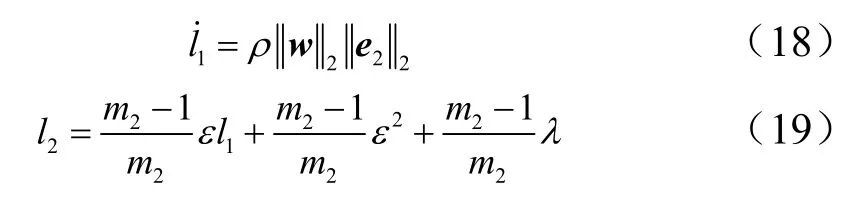
式中we为系统的增广状态22m≥ ；ρ为控制器设计参数；ε，λ为任意正实数；1l，2l为自适应参数。于是有定理2。

定理2：对于姿态角速率子系统（2）在滑模干扰观测器和自适应光滑二阶滑模控制率式（17）～（19）的作用下，当22m≥且适当选取参数ρ以及观测器增益时，能使角速率跟踪误差2e及其导数有限时间趋于零。

证明：把式（17）代入式（2），得姿态角速率误差子系统，形式如下：

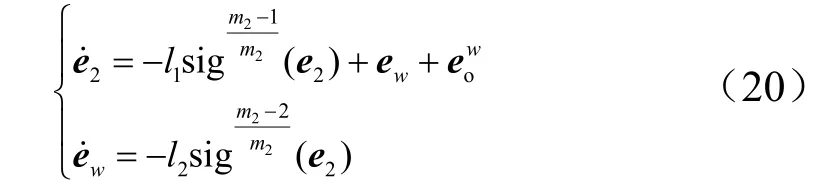
取Lyapunov函数为

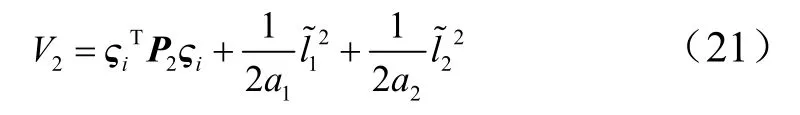
式中20V 为Lyapunov函数2V中首项。

对式（22）时间求导，有：

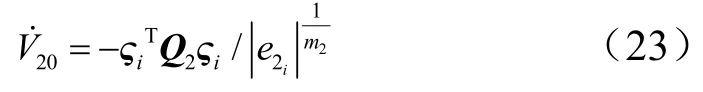
令：

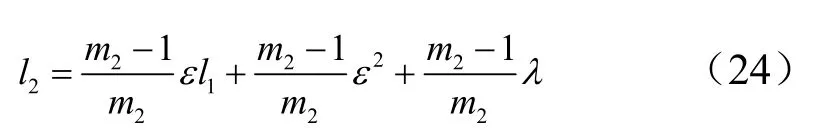
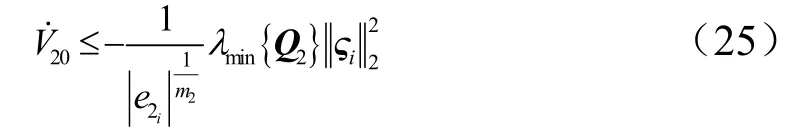
于是，式（25）可化为如下形式：

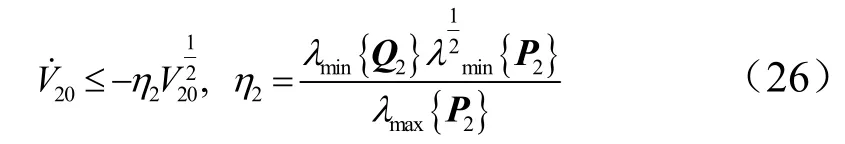
假设1l和2l界限为和，则任意 0t≥ 时即式（21）的导数有如下形式：

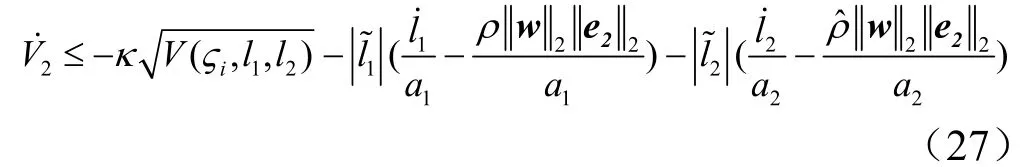
2.2 慢回路控制器设计

定义姿态角跟踪误差为

对式（28）两端求时间导数，并将式（1）代入，得姿态角误差子系统为满足

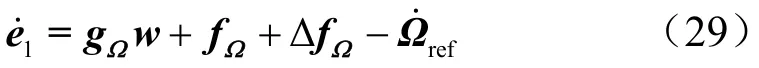
其中，δ为未知正数。根据2.1.1节中的观测器形式，可得能够在有限时间后收敛至零。

根据2.1节观测器和光滑二阶滑模设计方法，得到如下光滑二阶滑模控制律，能够使系统（1）有限时间稳定：

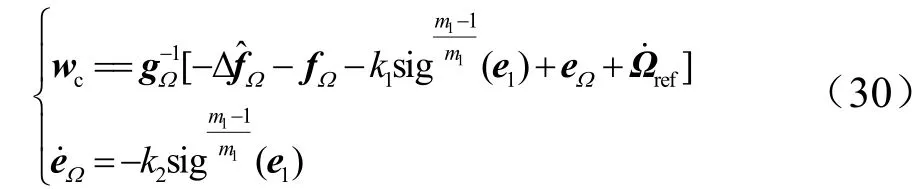
定理3：对于姿态角子系统（1），在干扰观测器和光滑二阶滑模控制率（30）的作用下，当且适当选取参数以及观测器增益能使姿态角误差1e及其导数有限时间TΩ趋于零。

证明：此处的证明过程与定理2的证明类似，因篇幅所限不继续证明。

3 仿真结果与分析

仿真中HSV的气动力及气动力矩系数拟合公式具体数据来源于文献[13]。

HSV的惯性矩阵为

飞行器飞行速度Ma=8.8，质量M=82 310 kg，航迹倾斜角γ=0。初始姿态角初始姿态角速率期望姿态角设为控制器及干扰观测器的仿真参数选取如下：

a）慢回路控制器参数设计：1m=3，1k=3.5，2k=1.5；

b）快回路控制器参数设计：2m=5，ρ=0.32，ε=0.01，λ=0.001；

c）滑模干扰观测器参数设计：1wα=2.5，2wα=0.01，

为了检验本文所设计的控制器对HSV姿态模型气动参数摄动的抑制作用，考虑了标称气动参数和气动参数摄动情况(取基于第 2节设计的自适应光滑二阶滑模控制器进行仿真研究。为了进一步验证本文所提控制策略的优越性，将其与传统滑模控制器做比较。图2～6为标称气动参数下的仿真结果。图 2为本文所提的控制器与传统滑模控制器的攻角、侧滑角和倾侧角的跟踪曲线。由图2可知，自适应光滑二阶滑模控制器具有较小的超调，能够快速准确的跟踪期望姿态角，且系统平滑无抖振，而传统滑模控制器存在抖振。

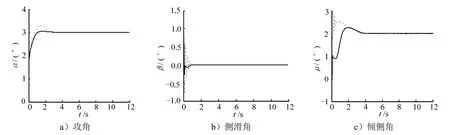
图2 传统滑模和自适应光滑二阶滑模控制器姿态角跟踪曲线对比（标称气动参数）Fig.2 Tracking Curves of Attitude Angles: Traditional Sliding Mode Controller via Adaptive Smooth Two-order Sliding Mode Controller

图3为传统滑模控制方法的滚转、俯仰和偏航速率响应曲线，从图3可知，虽然能够控制，但抖振明显；图4为本文所提控制方法的滚转、俯仰和偏航速率响应曲线，从图4可知，角速率变化平滑无抖振，控制精度高，收敛速度快；图 5为传统滑模控制器的气动舵偏响应曲线；图6为本文所提控制器的气动舵偏响应曲线，由图6可知本文所设计的控制策略使舵偏角偏转更小，且无抖振。

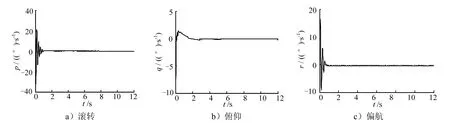
图3 传统滑模角速率响应曲线（标称气动参数）Fig.3 Response Curve of Roll, Pitch and Yaw Angular Rates: Traditional Sliding Mode Controller

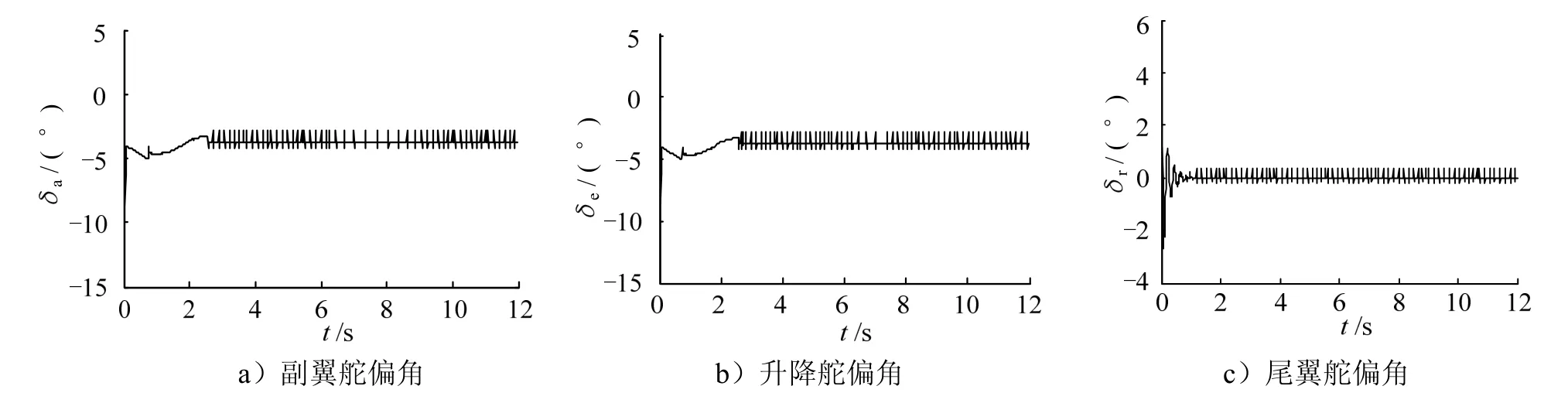
图5 传统滑模气动舵偏角响应曲线（标称气动参数）Fig.5 Response Curve of Aerosurface Deflections: Traditional Sliding Mode Controller

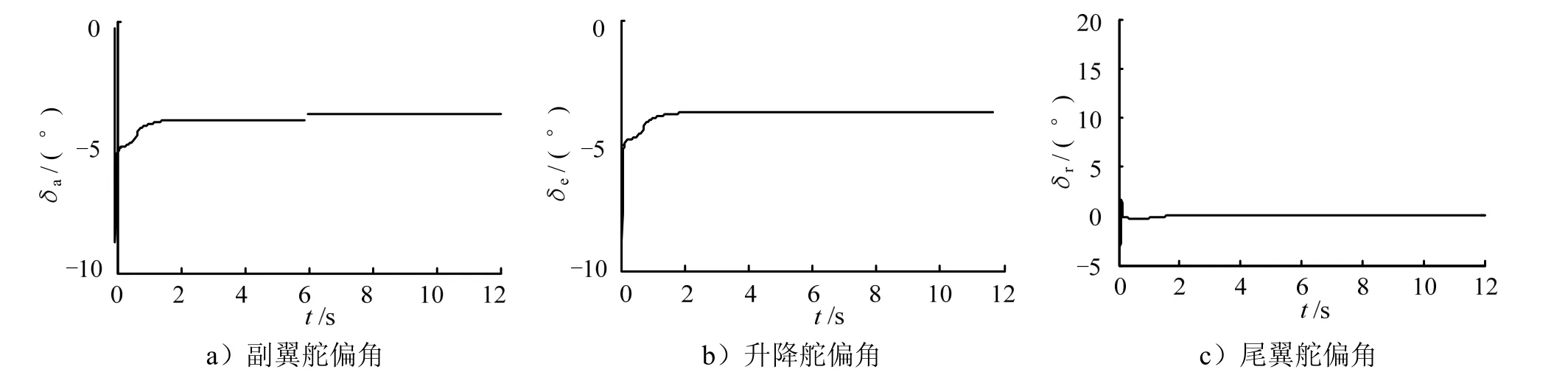
图6 自适应光滑二阶滑模控制器的气动舵偏角响应曲线（标称气动参数）Fig.6 Response Curve of Aerosurface Deflections: Adaptive Smooth Two-order Sliding Mode Controller

图7～11为气动参数增加40%情况下的仿真结果。从以上仿真曲线可知，在气动参数增加 40%情况下，本文所提控制策略仍能快速准确地跟踪期望指令，且曲线变化平滑无抖振；传统滑模控制器虽能跟踪，但调节时间增加较长，抖振更加明显。

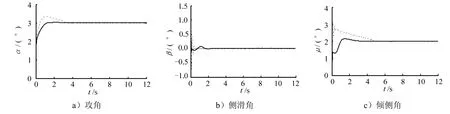
图7 传统滑模和自适应光滑二阶滑模控制器姿态角跟踪曲线对比（气动参数增加40%）Fig.7 Tracking Curves of Attitude Angles: Traditional Sliding Mode Controller via Adaptive Smooth Two-order Sliding Mode Controller

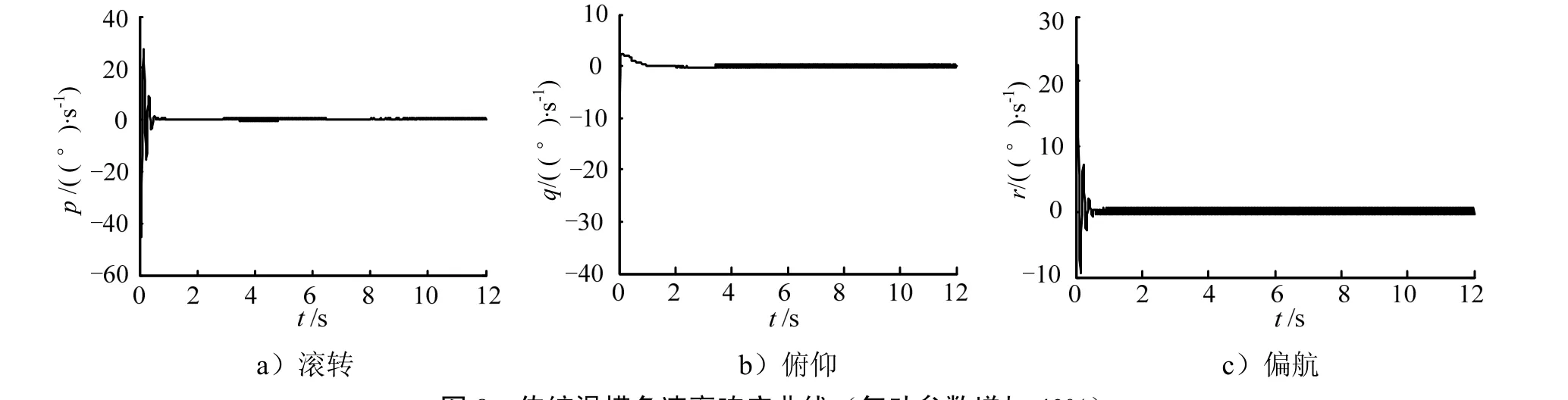
图8 传统滑模角速率响应曲线（气动参数增加40%）Fig.8 Response Curve of Roll, Pitch and Yaw Angular Rates: Traditional Sliding Mode Controller

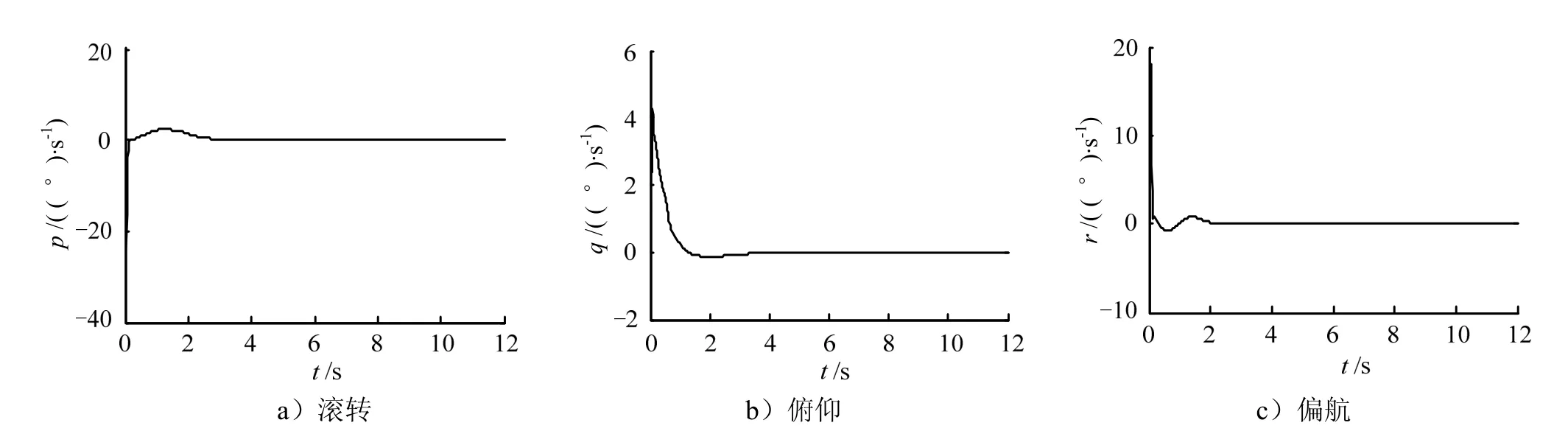
图9 自适应光滑二阶滑模控制角速率响应曲线（气动参数增加40%）Fig.9 Response Curve of Roll, Pitch and Yaw Angular Rates: Adaptive Smooth Two-order Sliding Mode Controller

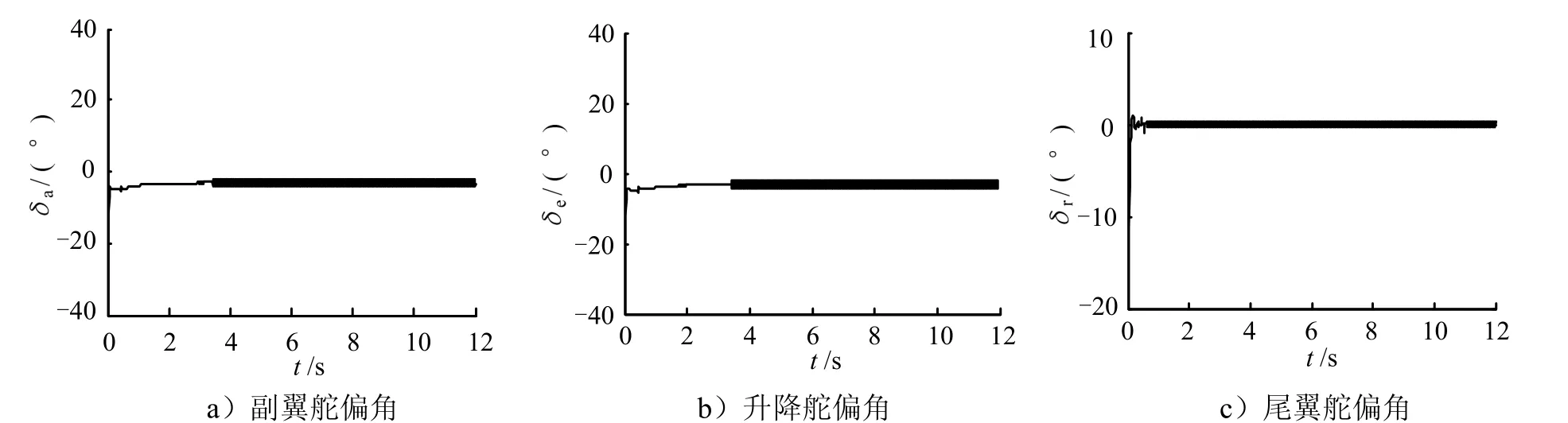
图10 传统滑模控制器的气动舵偏响应曲线（气动参数增加40%）Fig.10 Response Curve of Aerosurface Deflections: Traditional Sliding Mode Controller

图11 自适应光滑二阶滑模控制器气动舵偏角响应曲线（气动参数增加40%）Fig.11 Response Curve of Aerosurface Deflections: Adaptive Smooth Two-order Sliding Mode Controller

综上所述，本文设计基于滑模观测器的自适应光滑二阶滑模控制器对气动参数摄动具有良好的抑制作用，系统能够快速平稳跟踪姿态期望值，并且超调量小，控制器参数的自适应变化，提高了系统的控制精度。

4 结 论

本文针对具有气动参数剧烈变化的HSV姿态控制问题，基于滑模干扰观测器，设计了一种具有自适应特性的光滑二阶滑模有限时间控制策略。滑模干扰观测器对气动参数变化引起的不确定性进行了精确估计，自适应二阶滑模控制三轴姿态角快速稳定地跟踪期望值。基于Lyapunov理论证明了控制系统能够有限时间稳定。对气动参数剧烈变化时姿态控制系统进行了仿真研究，与传统滑模控制策略相比，本文所提的控制方法能够有效抑制气动参数变化，使姿态控制系统具有良好的控制性能和强鲁棒性。