关于方同轴线的一些研究

金少华 电子科技大学电子科学与工程学院 四川成都 610054

1.引言

作为一种时域模拟方法，时域有限差分法几乎可以分析所有电磁问题。波导器件结构比较复杂，一般方法很难分析，由于时域有限差分法灵活高效，可以方便地处理这些结构，时域分析各种波导传输线和波导不连续结构还可以应用时域有限差分法分析介质谐振器、波导耦合器和w波段滤波器等等。随着微波集成电路和单片微波集成电路的兴起，人们对时域模拟这类电路越来越感兴趣电路中可以具有有源和无源器件，也可以具有线性和非线性器件。因此，本文基于有限差分法研究方同轴线的色散特性，并和CST仿真结果进行对比，验证了有限差分法的优势和可行性

2.方同轴线色散问题

用有限差分法求下图所示四种传输线最低两个TM模的色散特性曲线，画出模式的横截面电磁场分布图。设b=5mm，ρ=a/b，ρ的取值范围为0. 3～0.7。

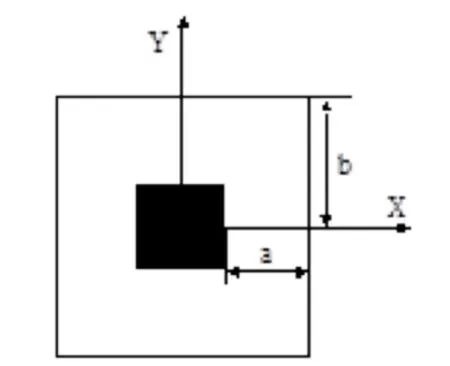
3. 有限差分法原理

假设同轴线壁由纯导体(σ→∞)构成，在同轴线中无自由电荷和传导电流(=0ρ，J=0)，同轴线间为真空，同轴线工作在匹配状态且截面均匀，所以在分析时仅考虑入射波。现只分析两个最低的TM模。将问题的求解归结为求解相应纵向分量zE所描述的定解问题。以φ标记相应纵向分量，在波导内， TM波满足的氦姆霍兹方程及边界条件为

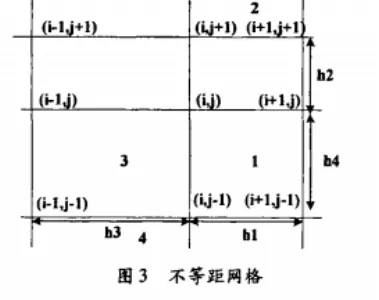
(1)对同轴线横截面进行网格离散化，如图2所示。设互方向和Y方向的步长相等。取h=0.5mm，a=3mm，b=5mm，对网格进行离散化。导出赫姆霍兹方程的差分形式。设场内某节点0处附近的各节点如图3所示，取步长不相等的一般情况，以 φ0、 φ1φ2φ3φ4分别代表在节点0、1、2、3、4处φ函数值

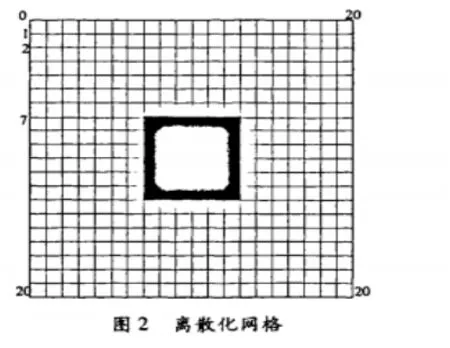
为了得到比较精确的差分格式，引入待定常数α、β对泰勒展开，构造如下关系式：

令系数为0，得到、之间满足

代入（2）式，舍去高阶项，得到 在式（2）中若令项系数为0，则得到、之间的关系：

将（5）式代入（2）式并忽略三阶以上的高次项，得：

同理可得：

（6）代入（7）得：

当 h1= h2= h3= h4= h ， 式（8） 就 可 以 简 化φ1+ φ2+ φ3+ φ4- 4 φ0= - ( kch)2φ0(9)

对导线外壁及边界C处，若网格线恰好和边界相重，则对任一边界上的节点a而言，令φ=Ez，则：f（10）

将上述各个差分格式分别应用于相应的网格节点，便可以得到以网格节点上待求场量φi(i=0,1,2,3...n)为未知数的n+1个差分方程，由此构成的差分方程组可用矩阵的形式表示为：[k][φ] = λ[ φ](11)

将上述问题归结为一矩阵的特征值问题。式中[K]为系数矩阵，[φ]是以网格节点上的待求场量φi为分量的列向量，而数值：（12）为特征值，称为截止波长。

由上述差分方程组求出所有的特征值。取出所有特征值中的最小值和次小的两个值，就可以求得两个最低TM模所对应的 k 值，由于并且得到cc(13) 即方形同轴线TM模的色散方程。

利用有限差分法离散化网格，取a=3mm，b=3mm，设x方向和y方向的步长相等，选取步长为h，频率范围在30G HZ- 6 0GHZ，采用Matlab仿真，得到方同轴线中TM波第一高次模，TM波第二高次模的色散曲线β～f以及横截面的电场和磁场图像如下所示： N=39，h=1/4(mm)x和y方向均为40格，matlab模拟图像如下：

4 软件仿真和数值模拟结果比较

4.1 数值模拟结果和仿真结果

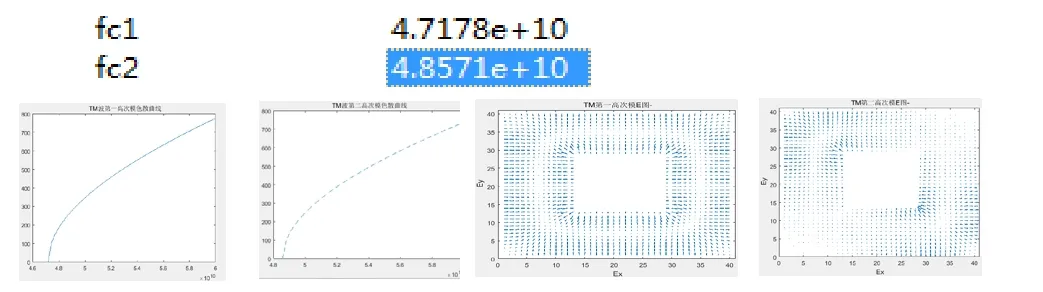
CST仿真结果如下；

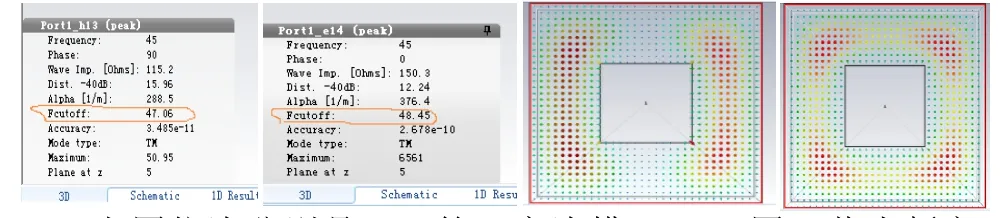
上图依次分别是：TM第一高次模（E、H图）截止频率；TM第二高次模（E、H图）截止频率；TM第一高次模E图 ；TM第二高次模E图；

6.总结

有限差分法是以差分原理为基础的一种数值方法，它实质上是将电磁场连续域问题变换

成离散系统的问题来求解，也就是通过网格状离散化模型上各离散点的数值解来逼近连续场域的真实解。

本次报告说明，有限差分发确实可以用于求解电磁场连续域问题，并且解的精度和网格剖分数目，即步长有关，步长越小，求解结果越准确。