不同间距对旁靠浮式系统的影响

(江苏科技大学船舶与海洋工程学院，江苏镇江 212003)

在目前的船舶与海洋工程领域中，我们会面临很多多浮体结构协同作业问题。本文基于粘流理论及计算流体力学理论，利用较成熟的CFD商业软件STARCCM+，对两旁靠浮式结构与系泊系统间的流场和运动问题进行了数值模拟分析，主要研究了旁靠浮式系统在不同间距情况下的水动力参数的对比，并对于系泊缆绳的受力情况进行了详细的分析。

1 基本理论

1.1 流体的基本控制方程

流体的流动要满足以下基本方程：

(1)质量守恒方程。在流体力学中，控制体中的质量通量，随着时间的推移，与控制物体的质量的加值，是零。对系统来说，质量守恒的原则是物体的质量在流体运动中保持不变，换句话说，物体的质量随时间而变化的绝对值为0。连续性方程是流体力学中质量守恒定律的表示。

由此，得出连续性方程的公式:

(1)

对于不可压缩流体，连续性方程简化为:

(2)

注:其中ρ表示流体密度；u、v、w分别表示流体速度在直角坐标系x、y、z轴的分量。

(2) 动量守恒方程。对于流体系统来说，单位体积内总的动量随时间变化率与作用于其上的外力之和相等。所受到的外力包括质量力和表面力。此定律的具体表达式即为运动方程(N-S方程)。

1.2 自由液面的捕捉方法

软件通过基于自由表面的全六面体非结构化网络技术来捕获方法用于解决粘度平均雷诺方程,空气和流体作为一个流体计算同时,单个流体的密度和粘度系数是由一个c函数得出。

构成函数c的求解方程式：

(3)

其中，V为控制体，S为围成控制体的面积，U为速度，Ud为S上方向的速度。

1.3 系泊链力的方程

将系泊链看作弹簧，系泊链的张力为：

FML=KΔL+T

(4)

其中，K为系泊链的刚度，ΔL为系泊链的长度变化量，T为系泊链的初始张力。

根据牛顿定律求解体的运动时要考虑到系泊链作用于体的力，即：

F+FML=ma

(5)

其中，F为作用于体上的流体力，a为体的加速度

2 不同间距对旁靠浮式系统的分析

2.1 不同间距计算模型的说明

两旁靠浮式结构选取两模型之间的窄缝间距为0.05 m，入射波为线性规则波，波高为0.035 m，初选波浪周期为0.98s(对应波长1.5 m)。模型参数如表1。

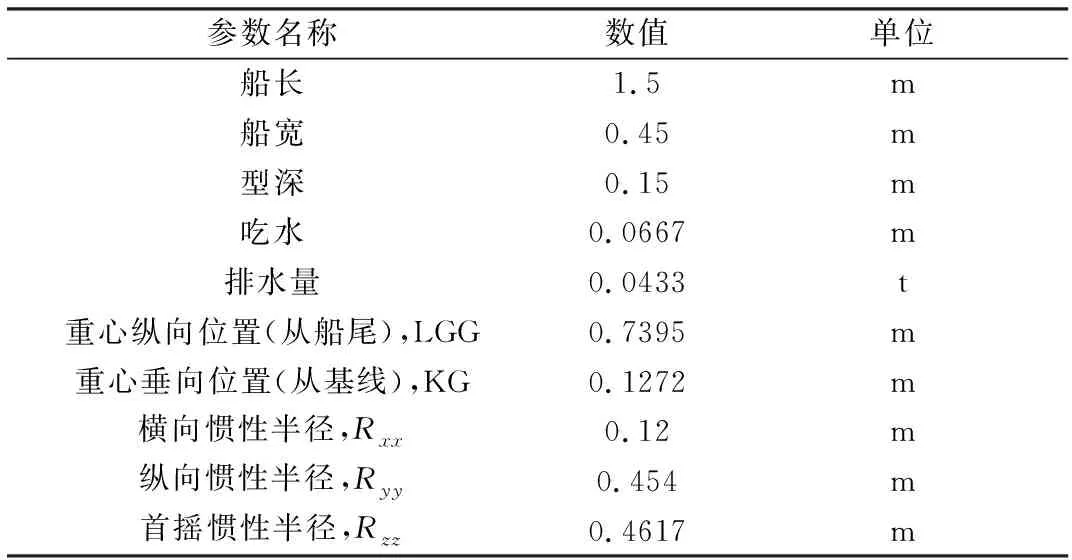
表1 模型的主要参数

4条缆绳编号分别从上方的左至右命名为1和4，从下方的左至右依次为2和3，上方浮体命名为B,下方浮体命名为A。系泊系统的初始力为0，刚度为16.35 kN/m。

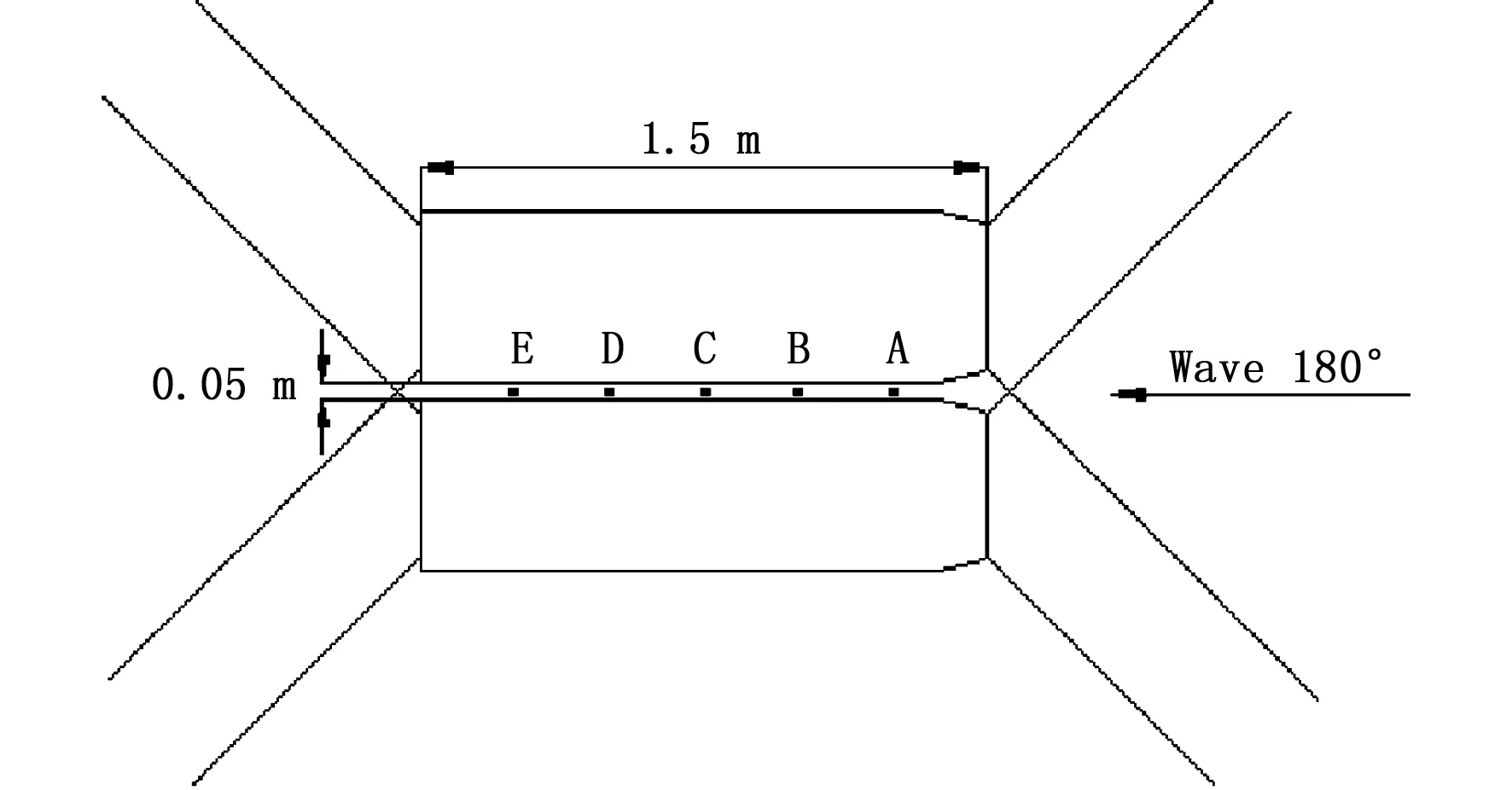
图1 系泊系统的布置图

2.2 不同间距对于两旁靠浮式结构运动的影响

根据介绍的旁靠多浮体系统有多种形式，本文对多浮体结构进行简化处理，选用两个完全相同的均质方型模型，旨在观察其中的规律和变化情况。选取完全相同的均质方型模型， 间距分别为0.05 m、0.1 m和0.15 m。

图2至图7给出了间距分别为0.05 m、0.1 m和0.15 m时，两旁靠浮式结构物的横摇(Rx)、纵摇(Ry)、艏摇(Rz)、纵荡(Tx)、横荡(Ty)、垂荡(Tz)运动的对比。

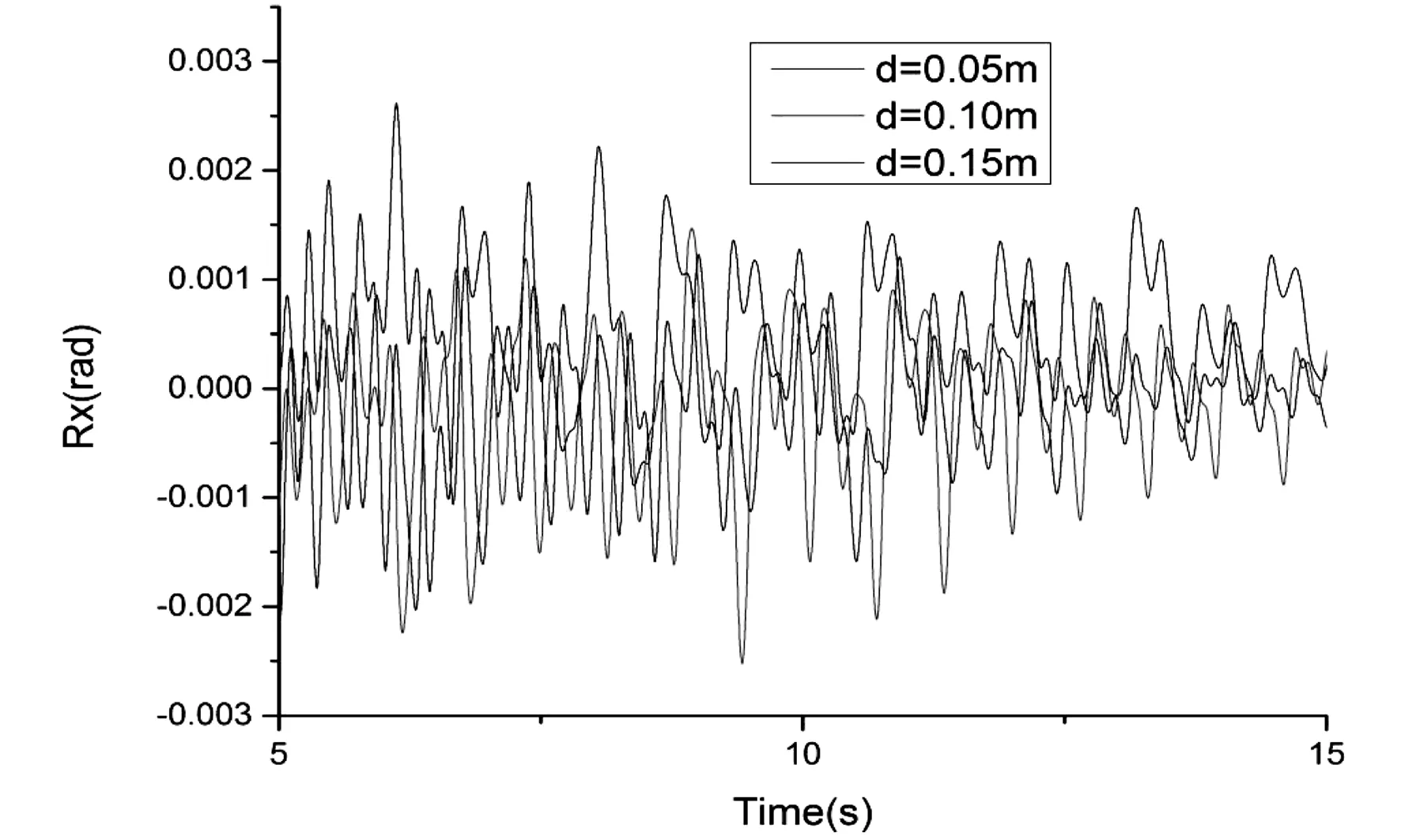
图2 横摇Rx运动的时历曲线对比示意图

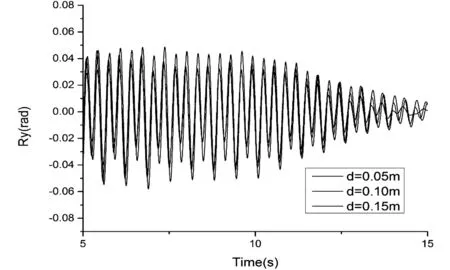
图3 纵摇Ry运动的时历曲线对比示意图

图4 艏摇Rz运动的时历曲线对比示意图

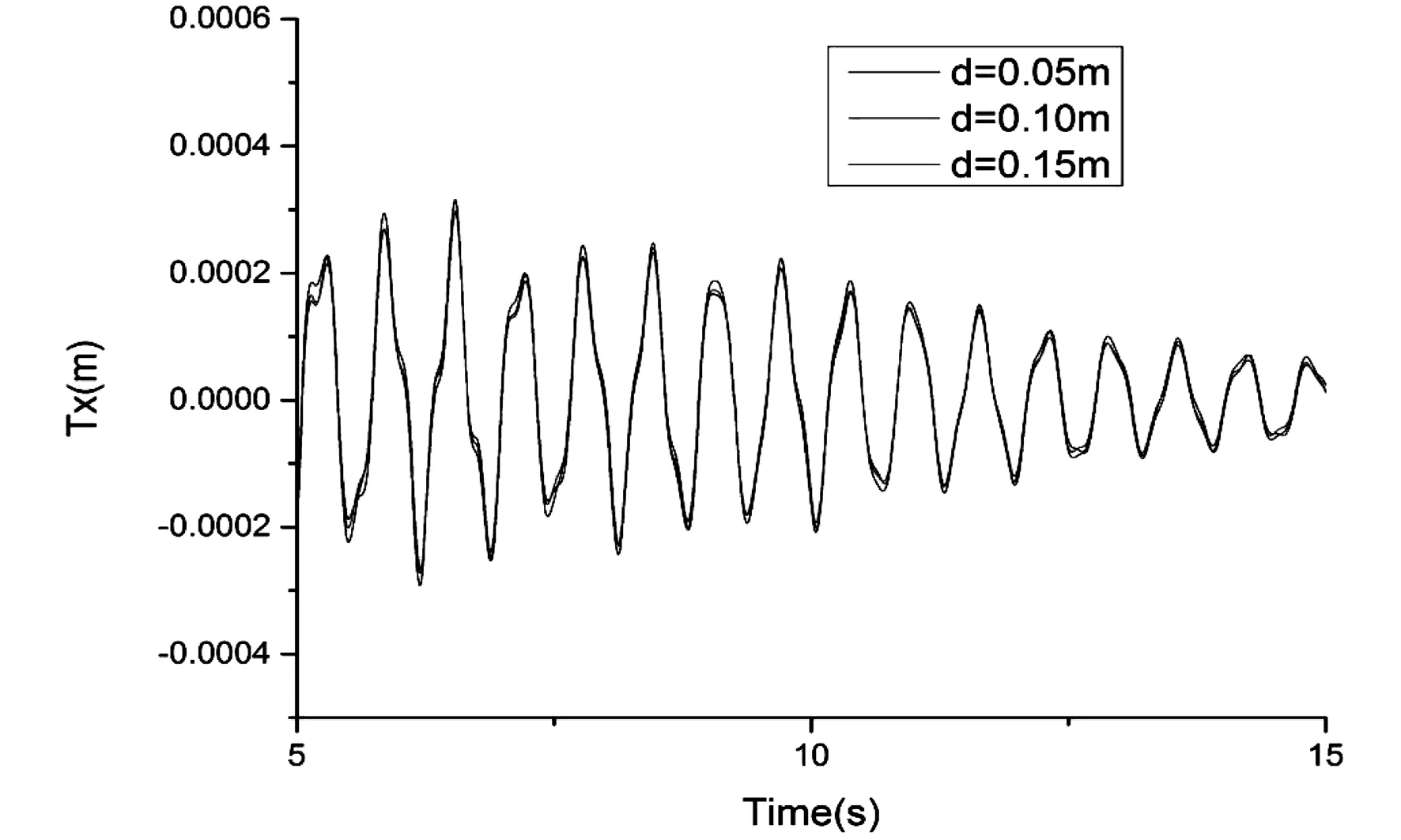
图5 纵荡Tx运动的时历曲线对比示意图

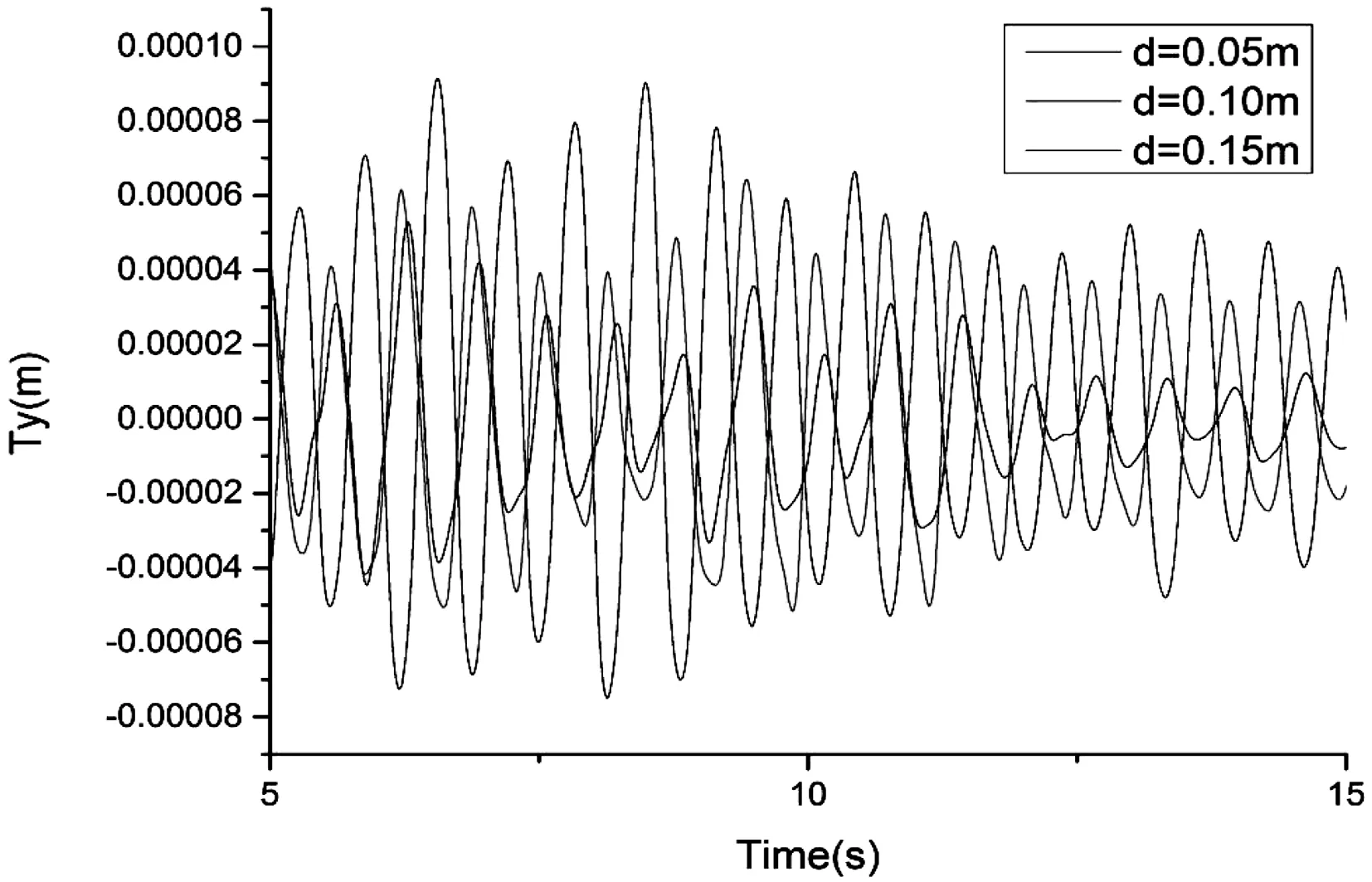
图6 横荡Ty运动的时历曲线对比示意图

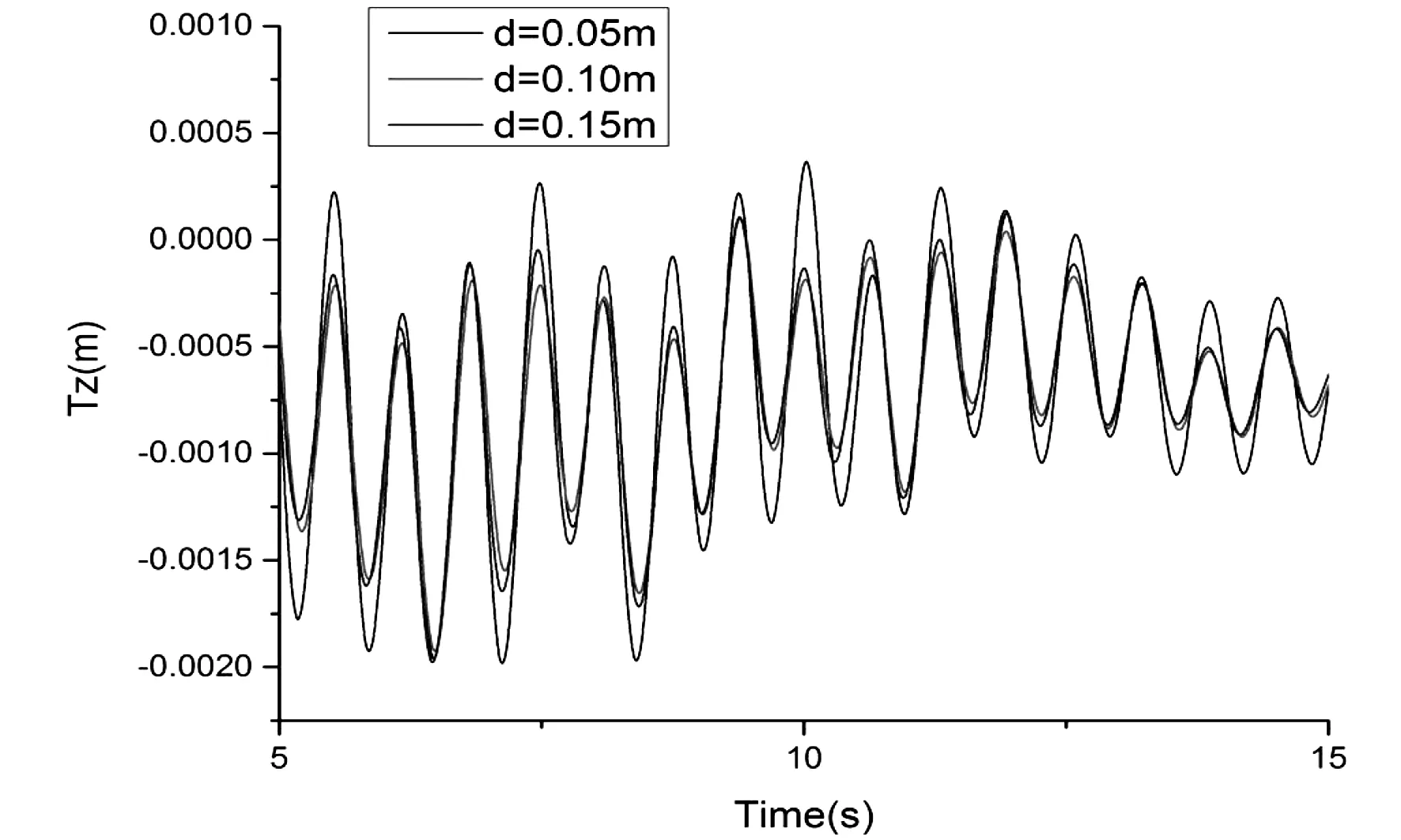
图7 垂荡Tz运动的时历曲线对比示意图

由图2至图7可知，在浮体系泊状态下，浮体六自由度的运动在不同间距的情况基本上比较吻合，差距非常小，且整体运动的变化幅度十分切合。总体来说纵摇、艏摇和横摇要明显强于垂荡、纵荡和横荡三种情况，很有可能是系泊系统的固定使得后三种运动不是很明显。在纵荡时，三种间距下运动基本上重合，很有可能是系泊系统是沿x轴布置，所以导致纵荡时在不同间距下的运动吻合比较明显。但是在横荡时在间距越来越大的情况下，在10秒以后运动的幅度却越来越小，很有可能是两浮体的互相影响逐渐减小，从而导致运动的变化程度缩小。这些变化比较小的原因，极有可能是缆绳系泊的限制，导致浮体六自由度运动都比较小。对比上述运动发现，间距越小，浮体运动越来越厉害，极有可能是因为两浮体相互间的影响导致，从而对两浮体间的运动产生了相互影响。

因此，间距的大小对于船舶的运动有一定的影响。但在本文中的差距不是很明显，所以很有可能是间距的差距取得比较小，并且有系泊系统的约束，所以以后可以通过适当增大两旁靠浮体的间距梯度的方法，并适当修改系泊系统的参数，从而来达到更好的研究效果。

2.3 不同间距对于两旁靠浮式结构缆绳受力的影响

以下给出了在不同间距状态下，两旁靠浮式结构物缆绳受力的对比，如图8至图11。

图8 A1缆绳在不同间距情况下缆绳受力的时历曲线对比示意图

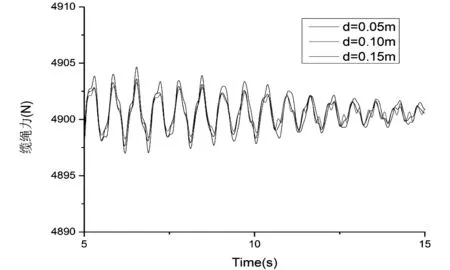
图9 A2缆绳在不同间距情况下缆绳受力的时历曲线对比示意图

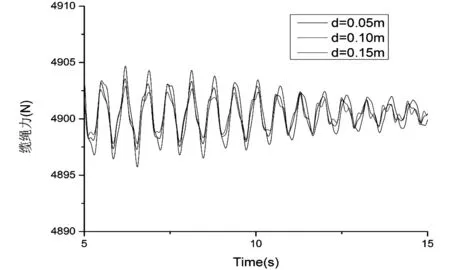
图10 A3缆绳在不同间距情况下缆绳受力的时历曲线对比示意图

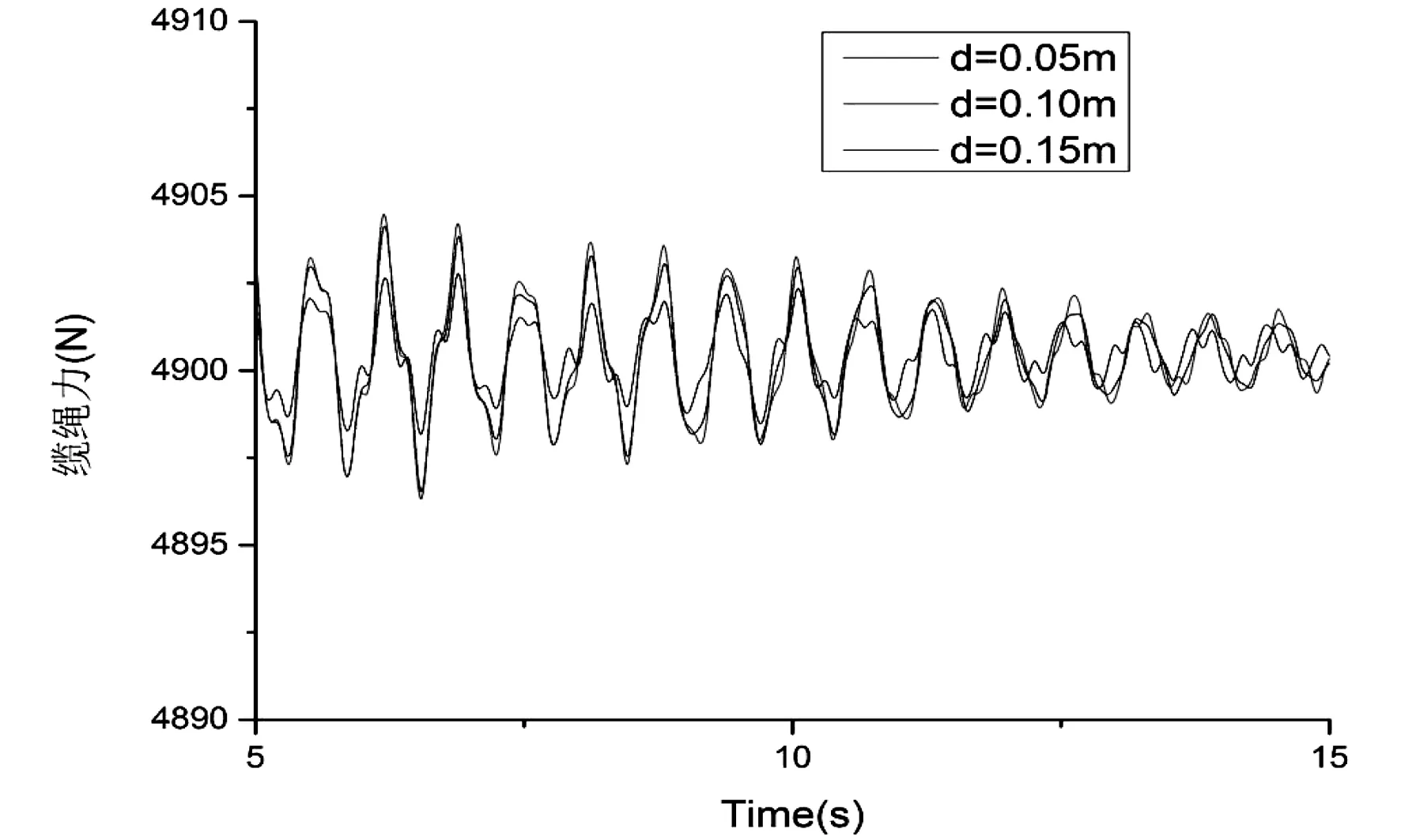
图11 A4缆绳在不同间距情况下缆绳受力的时历曲线对比示意图

由图8至图11可以看出，在3种间距情况下，缆绳的受力变化幅度比较集中，都显示4895-4905N之间，受力的变化程度不是很大，很有可能是两浮体的间距相对变化程度较小，所以对缆绳受力的变化影响相对变得较小，以后可以通过适当增大两旁靠浮体的间距梯度的方法，从而更好的研究出间距对于系泊缆绳的受力变化的情况。至于四条缆绳的受力变化情况都比较集中，且受力变化都比较接近，变化的趋势都十分的接近。都集中在4890-4910N之间，基本上处于重合的趋势，变化幅度稳定在20N左右。

由此我们可知，不同的间距可能对于系泊缆绳受力的变化影响不算很大，以后可能适当加大间距梯度的方法，可能可以看出更加明显的变化。

4 不同间距对于两旁靠浮式结构波面升高的影响

不同间距时，提取一个周期内4个时刻的波面云图，如图12至图14所示。

图12 间距0.05m时一个完整波浪周期内的波面变化云图

图13 间距0.10m时一个完整波浪周期内的波面变化云图

图14 间距0.15m时一个完整波浪周期内的波面变化云图

本次模拟的波长均为1倍船长。在观察波面云图时，我们可以发现：当入射波波峰传递到两船首时，波面升高情况十分明显。随着波浪的不断传播，峰值点不断后移，并且以相对较缓的幅度持续减小，随后波面趋于稳定。可以看出由于两船的相互影响，在共振波浪作用下，两船间距内部水体发生共振，运动剧烈，导致明显的波浪放大，而在船尾后波高迅速降低，趋于稳定，并在传播到水池右端时成功消波。综上所述，间距越小，两浮体间距内的振动越明显，波面升高情况也更为明显。

3 结 语

本文基于粘性流体力学理论以及计算流体力学(CFD)理论，自由液面的捕捉采用VOF法，使用STAR-CCM+软件对不同间距对系泊浮式结构的影响进行分析，得出以下结论：在不同的间距情况下，浮体六自由度的运动在不同间距的情况基本上比较吻合，差距非常小，且整体运动的变化幅度都十分切合。两浮体之间存在一定的影响，但由于系泊缆绳的约束，造成之间的影响较小，从而使浮体运动更为稳定。