一种基于Boltzmann方程的碳基复合材料氧化烧蚀微观界面的追踪方法

袁经超， 朱子镝， 张方舟， 张 丹， 张伟刚， 李爱军

(1. 上海大学 材料科学与工程学院，上海 200072；2. 上海大学 机电工程与自动化学院，上海 200072； 3. 中国科学院过程工程研究所 多相复杂系统国家重点实验室, 北京 100190)

1 前言

炭纤维增强碳基体(C/C)复合材料的超高温烧蚀机理受到化学动力学和对流-扩散机制的双重控制，在烧蚀过程中会依次出现氧化和升华[1-4]。但碳基复合材料的纤维相和基体相具有不同的抗氧化与升华能力，因此在高温环境下材料的表面会产生不均匀的退让，引起表面粗糙度的变化。进一步，在热气流的冲击下，露在外面的纤维受剪切力和旋涡阻力的作用会产生剥落，造成不可预期的表层型面变化。降低了结构的稳定性和可靠性，增加了结构失效的风险[5,6]。为了对机械剥蚀更好地进行预测，细观尺度上化学烧蚀形貌演化过程的建模和计算尤为重要。

碳基复合材料烧蚀过程的实质是一个多相界面的演变过程，影响因素众多。当前已进行了大量的实验研究，如电弧喷射试验[7]、热重法[8,9]和氧乙炔烧蚀试验[10-12]等。不少研究者在试验观察碳基复合材料的烧蚀形貌的基础上，采用了不同尺度的计算方法，如有限元[13]、VOF[14-16]和Level-Set[17,18]方法对烧蚀过程中界面的演变进行了数值模拟，为理解碳基复合材料的烧蚀行为提供了有效的途径。其中，Vignoles等[19]提出的基于布朗运动的随机行走模型，成功预测了碳基复合材料单胞烧蚀的形貌变化。在这个模型中，假设气相组分在气固界面处被迅速消耗，浓度呈线性变化；高温氧化反应被简化为粘附事件概率，并与反应速率常数直接相关联。模型的不足之处在于，粘附概率的选取对于该模型的有效性起到决定性作用，然而其物理意义却并不明确，并且主要还依赖于经验系数，必须经过反复的优化方能确定。同时布朗运动模型为概率模型，需对单个粒子运动进行模拟，所需计算资源较大，且每次计算均引入随机误差，计算效率低，当应用两相以上情况时模型复杂程度会急剧提高。

笔者采用Boltzmann方法模拟含纤维/基体界面相的碳基复合材料烧蚀界面的演化过程。作为一种介观数值模拟方法，Boltzmann同时具有微观与宏观方法的计算优势，易应用于复杂的几何域[20]，易追踪多相界面[21]，并且具有良好的并行性[22]。同时参考相场模型处理多相问题的方法，引入空间占有率概念，在Euler网格下，针对三相单胞模型实现了气相组分浓度的预测和烧蚀界面的自捕捉，弥补了前人模型的不足。

2 单胞烧蚀模型

当前，单胞烧蚀模型是被众多研究者所认可的[17,19,23,24]，可以反映碳基复合材料介观尺度上烧蚀行为的一个理想简化模型。如图1(a)所示，一根圆柱状炭纤维被埋在了不同材料构成的基体里面，而炭纤维相与基体相之间有一层非常薄的中间层。

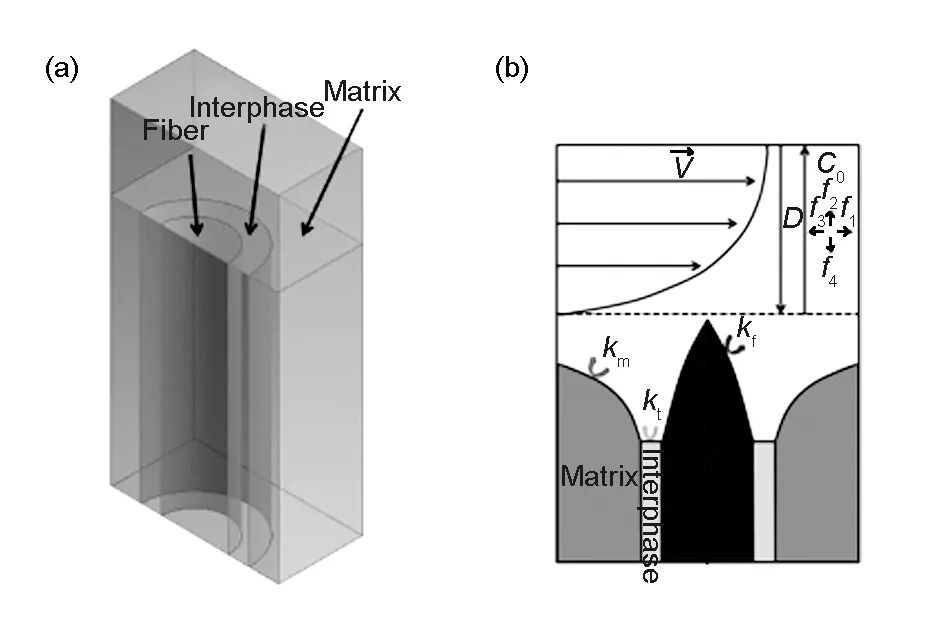
图 1 (a) 纤维/界面相/基体的单胞模型和(b) 烧蚀过程中单胞模型变化示意图

在初始时刻，C/C复合材料的表面是平滑的，炭纤维相与基体相完美贴合，高度一致。烧蚀过程中，高温氧气气流在材料表面高速流过，并形成一定厚度的边界层，如图1(b)所示。在边界层内部氧气几乎是静止的，边界层内部的主要传质是由浓度差引起的纯扩散过程[8]，可由Fick扩散定律进行描述：

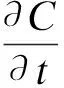
(1)

式中,C表示气体中扩散物质的浓度；D表示扩散物质的扩散系数。在边界层外部，对流传质将占主导地位，相较于边界层内部，边界层外部的氧气浓度可以看作是不变的，可采用Dirichlet边界条件[19]：

C=C0

(2)

整体材料可以认为是单胞模型的重复，所以横向边界采取周期性边界条件。

温度在898 K左右时，氧化反应为体系中的主要化学反应[8]，这时碳基复合材料的烧蚀是以碳的氧化反应为主要反应。可简化为如下化学反应方程式：

Cs+O2(g)CO2(g)

(3)

假设这是一个一级动力学反应[5]，氧气在材料表面与材料发生反应，可以认为氧气和材料一起从这个体系中移除，材料表面处根据反应速率和局部反应物浓度得到流出通量：

DC·n=k·C

(4)

其中,n为表面单位法矢量；k为表面反应速率常数。随着反应的进行，材料表面会发生退让。尽管控制方程的形式很简单，但对于非均匀材料，表面的这种退让会运动更加复杂，由于不同相具有不同的反应速率常数，使得烧蚀表面会出现类似波动的变化，这极大地提升了求解难度。尤其对于两相以上的复杂情况，难以得到解析。

3 数值模拟方法

格子Boltzmann方法在求解复杂流场问题上有很好的优势，且可方便地拓展多路径的化学反应过程。基本的BGK格子Boltzmann方程如下[22]：

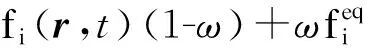
+ΔtwiS

(5)

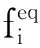
通过Chapman-Enskog展开可以建立宏观的扩散系数与微观的碰撞频率之间的关系[22]：

(6)

式中,Δx表示极小的空间步长，各个方向的空间步长相同,d表示维度。

对于二维轴对称问题，需额外添加一项以应对径向空间的变化[25]。

(7)

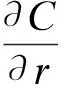
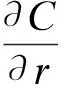
(8)

式中r表示圆柱的径向,j表示径向的离数，f1和f3方向由图1(b)给出。式(8)较(7)更为精确[25]，式(7) 或者(8)可以直接添加进源项。

尽管带有源项的BGK格子Boltzmann方程可以很好地描述含有均相体反应的扩散-反应体系，但碳基复合材料的不均匀性，使得数值算法必须面对非均相表面反应体系。为此，参考相场模型的处理方法，构建一个新的变量Φi(0≤Φi<1)用于区分不同的固体与气体，0表示不存在固相i，1表示完全为固相i。Φi代表的是某一种固相i在空间的占有率。引入Φi之后，氧气与固相i反应的消耗量Ri，即式(4)中的流出通量，可以通过含Φi的式子表示：

Ri=ΦikiC

(9)

固相i对应的烧蚀量可以通过氧气的消耗量Ri得到，因此Φi可以表示为：

(10)

式中,Mi表示固相i的分子质量；ρi表示固相i的密度。Φi值的求解可确定材料内不同固体相所占比例。

4 结果讨论

4.1 结果验证

Vignoles等[5]在一定假设下对只包含基体和纤维相的单胞模型求得解析解。基体相较纤维拥有更高的反应活性，即更大的反应速率常数[8]。解析解表明：由于基体的反应速率大于纤维，基体表面率先发生衰退，使得纤维逐渐露出，进而纤维侧向开始被氧化，使得纤维逐渐变细，最终变为针形；两个重要的参数可反映出稳态下单胞的表面粗糙度，即基体与纤维的反应活性对比A以及舍伍德数Sh。

(11)

(12)

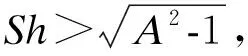
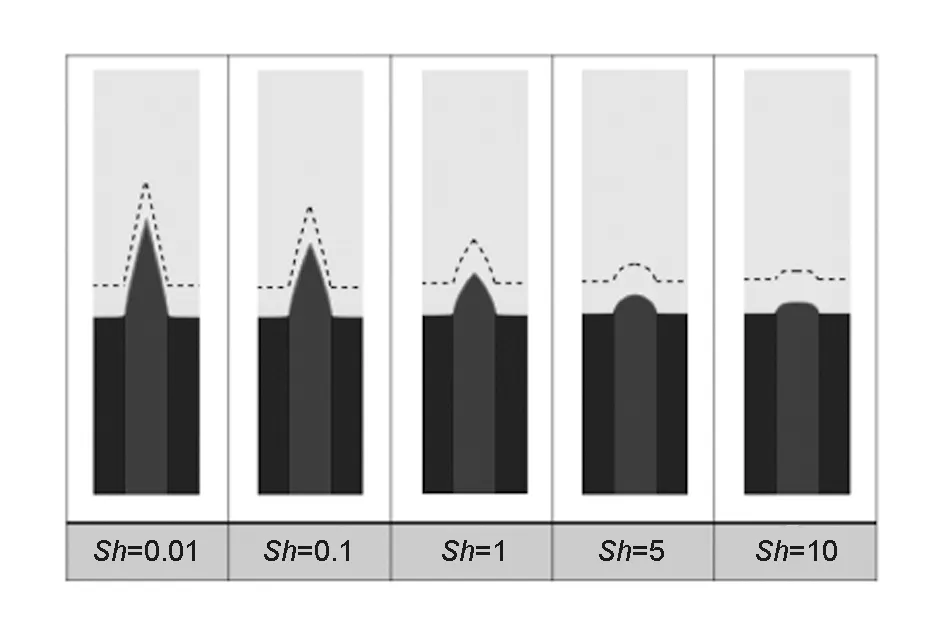
图 2 两相单胞模型的数值计算结果与解析解的对比(A=5)

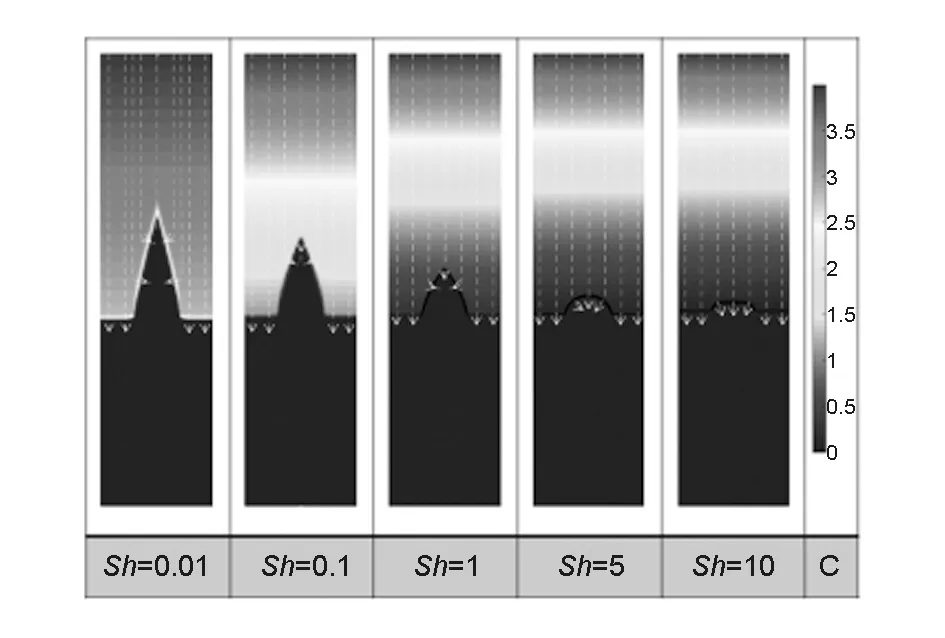
图 3 两相单胞模型浓度场和质量传输流线 (A=5)

Vignoles等[5]在计算解析解时假设氧气浓度延垂直方向呈线性变化，而水平方向无变化。本文的模型无需此假设，可同时计算出气相的浓度场。图3为烧蚀达到稳态时氧气浓度的等值线，显然，在远离烧蚀界面处水平方向上不存在浓度梯度，假设成立，横向的浓度传递可以忽略。而在烧蚀界面附近，等值线沿着表面发生曲折，表明水平方向上也存在有浓度差。图3进一步表明，扩散限制模式下(Sh远大于1)，固体表面极大的反应速率，使得固体表面浓度几乎为0，氧气从边界层顶部源源不断向表面扩散；反应限制模式(Sh远小于1)，由于反应速率远小于扩散速率，所以整个边界层内部浓度均达到边界层外部浓度C0。仅在反应限制模式下，不需要计算浓度场，可将材料非均相的性质解耦出来计算。

4.2 纤维和基体界面相

碳基复合材料在炭纤维与基体之间往往存在一个界面相，是增强相与基体相连接的桥梁，也是应力的传递者。通常界面相较于基体有更为活泼的化学性质，即拥有更大的反应速率常数[5]。因此包含中间相的单胞模型更接近C/C复合材料的真实状态，同时也可以进一步检验算法在更为复杂的多相材料烧蚀问题求解的稳定性。本文在基体和纤维不变的情况下，加入了中间相，假设反应速率常数ki=8km。

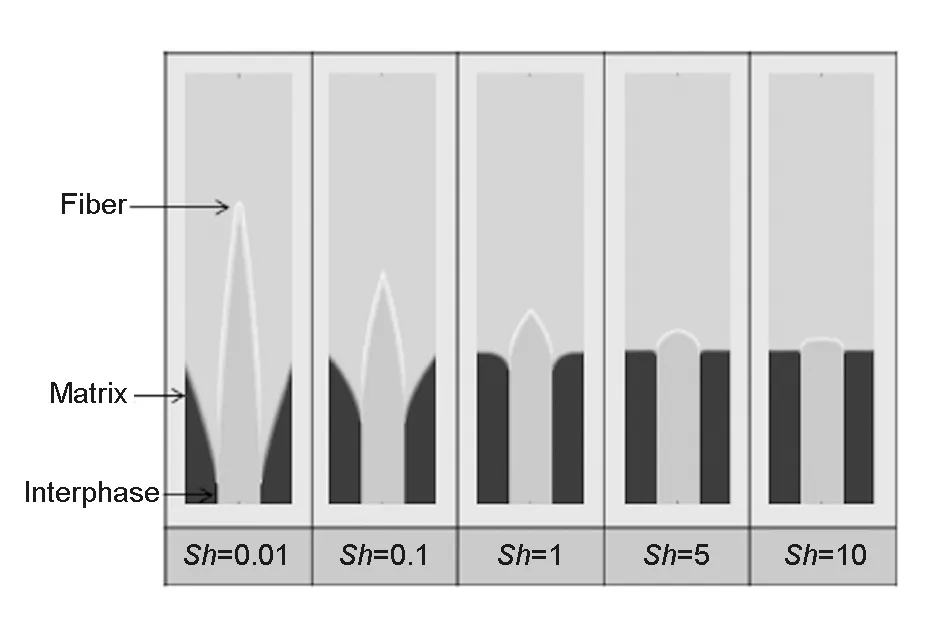
图 4 不同舍伍德数下三相单胞烧蚀模型的界面烧蚀形貌

图4为不同舍伍德数下，包含纤维-界面相-基体的单胞烧蚀模型的计算结果。如图4所示，在扩散限制模式下，材料的非均相性无法体现，烧蚀形貌与图2基本一致；而在反应限制模式下，材料的不均匀性明显体现，纤维露出高度，不论相对于基体还是界面相，都明显提升。由于界面相的反应速率常数大于基体的反应速率常数，所以体系中界面衰退最快的是界面相。界面相将基体与纤维分成了两部分，界面相与基体构成一个体系，与纤维构成另一个体系，分别与最初单胞模型一致。因此，对于每个体系主要的控制参数依然为舍伍德数Sh与反应活性比A。若将中间相的参数作为Sh和A的分子项，纤维—界面相系统参数可写为：

(13)

(14)

基体—界面相系统参数可写为：

(15)

(16)

图5中左图和右图分别是将包含基体-界面相-纤维的三相体系拆分成界面相-纤维和界面相-基体进行计算所得的结果。左图和右图相互叠加可以获得与中间图及其相似的结果。这表明对单胞烧蚀模型而言，多相材料的粗糙度取决于相邻两相之间的状态。相邻两相之间的作用不会受到其它相作用的影响。并且与相邻两相的厚度无关。但同时也表明：中间相作为化学反应最活泼的相，会增加纤维的露出高度，增大材料整体的表面粗糙度。

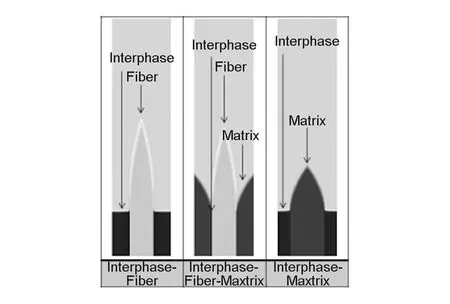
图 5 三相模型与两相模型对比

4.3 烧蚀深度

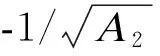
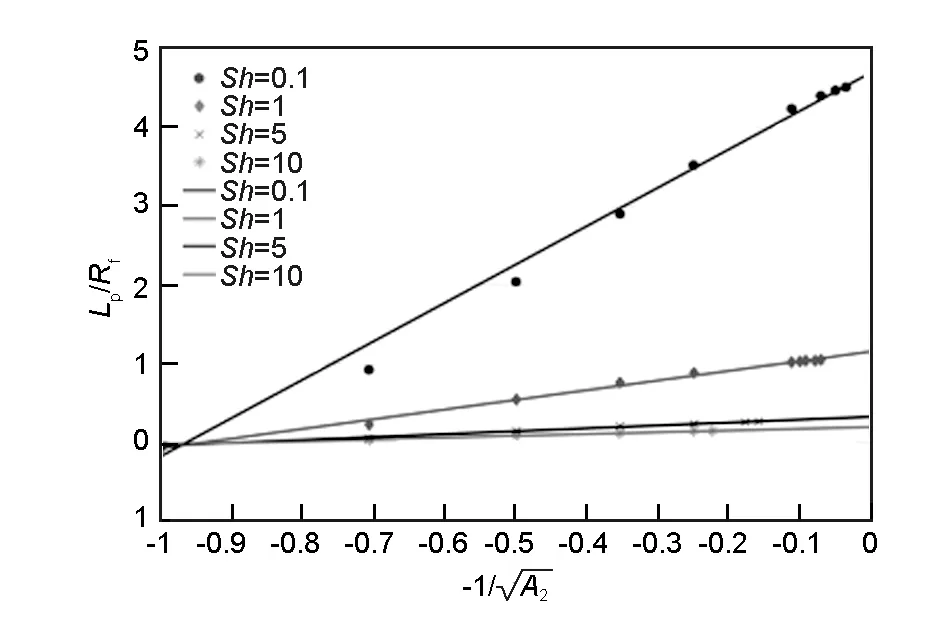
图 6 反应活性比(A2)与烧蚀深度(Lp)的关系(A=5)

烧蚀极限Lpm深度在Rf确定时仅与Sh相关，对此对Lpm进行无量纲转换，并且做出与Sh相关的图7。图7表明了Sh与Rf/Lpm的线性关系，黑色点为图6中各个Sh下的极限烧蚀深度Lpm，实线为线性的拟合函数，虚线是根据现有点数据所构成的误差边界，菱形点为随机选取Sh模拟结果，用来验证预测模型的可靠性。

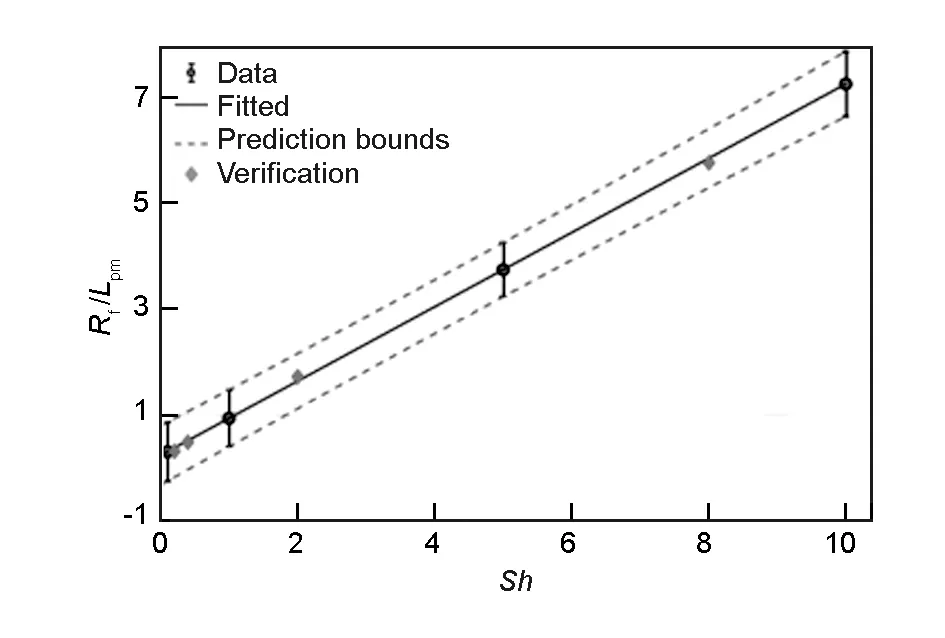
图 7 舍伍德数(Sh)与极限烧蚀深度(Lpm)之间的关系(A=5)

显然验证点很好的落在了预测边界以内，这表明预测的直线具有很好的准确性。此外，这条直线近乎于通过(0,0)点，Sh趋向于0的时候，即基体和纤维的反应系数趋向于0，理论上烧蚀深度应该趋向于，然而这里存在稳态的概念，一般烧蚀轮廓不发生变化时即为稳态，而(0,0)处不存在稳态的情况，所以Rf/Lpm受到扩散与达到稳态的时间影响，具有一定深度。另一方面，直线的斜率代表了气相扩散进入烧蚀孔内的传质阻力，气相一边与基体与纤维反应，一边扩散进入烧蚀孔内部，达到稳态时，扩散最深的状态便是烧蚀的最大深度。若假设截距为0，斜率可由任意Sh下的一组数据估计，由此可以估算出其他Sh下的Lpm，即可预测任意体系下的烧蚀深度或者露出高度。可拟合出如下关系式：

(17)

5 结论

基于Boltzmann方法，通过构建空间占有率参数Φi，提出了扩散—表面非均相反应体系的新算法。该算法应用于纤维—基体两相单胞模型时，计算结果与解析解具有很好的一致性，验证了算法的可靠性。并且可以获得以往数值算法无法得到的浓度场的信息。气相浓度的线性化假设在远离界面处具有合理性，但在界面附近明显呈非线性分布。进一步，将算法用于求解纤维-基体-界面相的三相单胞模型。氧化烧蚀的形貌仅取决于相邻两相之间的状态。含界面相的氧化烧蚀，存在最大烧蚀深度。并且通过数学变换可以得到烧蚀深度与各参数之间的关系，提出了预测烧蚀深度的数学表达式。在求解过程中，提出的算法在多相结构计算中表现出了良好的稳定性。