横向少约束体系超宽箱梁空间效应分析

杨顺刚

(重庆市武隆区交通委员会，重庆 408500)

为保证城市路网交通的快捷、安全、畅通，城市道路随着城市的快速发展而不断拓宽。以桥梁为例，目前，我国城市路网特别是城市主干道，路幅宽度超过40 m的桥梁越来越多，部分达到了80 m以上，导致桥梁宽跨比(W/L)大，甚至超过了1[1-2]，其相应的结构布置、构造、设计方法及施工工艺等较普通桥梁而言，均有较大差别。同时，因桥墩位置受到用地规划、桥下景观等因素的限制，不少桥梁结构呈现出宽度大、横向支撑少的特点，使得桥梁结构受力复杂，空间效应显著。

1 桥梁宽跨比对空间效应的影响

相关研究表明，宽跨比是影响箱梁内力空间分布不均匀的主要因素。对于宽跨比较大的桥梁结构，其受力特点已显著不同于梁受力体系，而趋向于梁板受力。本文对跨度L分别为30 m、35 m、40 m、45 m、50 m、55 m，桥宽W分别对应为[25,L] (步长5 m)的三跨等截面连续梁进行分析，研究宽跨比对空间效应的影响。

1.1 基本设定

(1) 箱梁采用等截面直腹板单箱多室截面，腹板中心线间距均为5 m，各桥幅宽度由增减箱室数量来适应。

(2) 不同跨度箱梁梁高均取为跨度的1/18。

(3) 各桥墩横梁位置均设置两个支座，支座间距设置原则为：均布荷载作用下，横梁支座处负弯矩值等于跨中正弯矩值。

(4) 暂不考虑横梁受力情况，横梁与箱梁梁高保持一致。

(5) 按梁格法计算[3-4]，对纵梁及虚拟横梁进行相应抗弯、抗扭刚度修正。

1.2 内力不均匀系数

由于宽箱剪力滞效应的存在，箱梁各腹板受力不均匀，而腹板内力是结构设计时最重要的关注对象[5]。本文拟定以下4个自重作用下的内力不均匀系数：λ1为墩顶负弯矩不均匀系数；λ2为中跨跨中正弯矩不均匀系数；λ3为边跨跨中正弯矩不均匀系数；λ4为墩顶竖向剪力不均匀系数，各不均匀系数为受力最大腹板与受力最小腹板相应内力值之比。

1.3 宽跨比对内力不均匀系数的影响

箱梁自重作用下不同宽跨比各中腹板内力不均匀系数如图1所示。

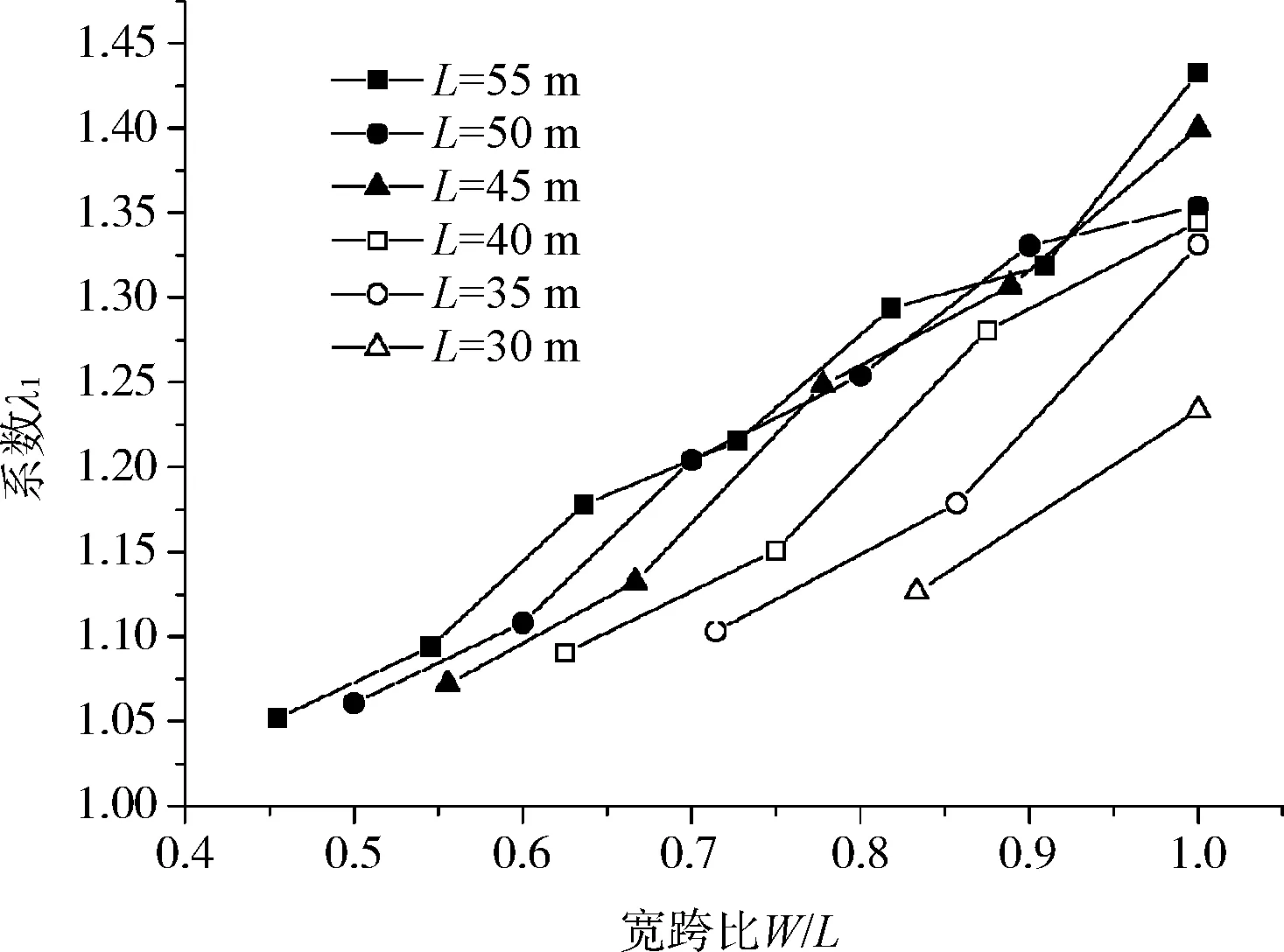
(a) 不均匀系数λ1

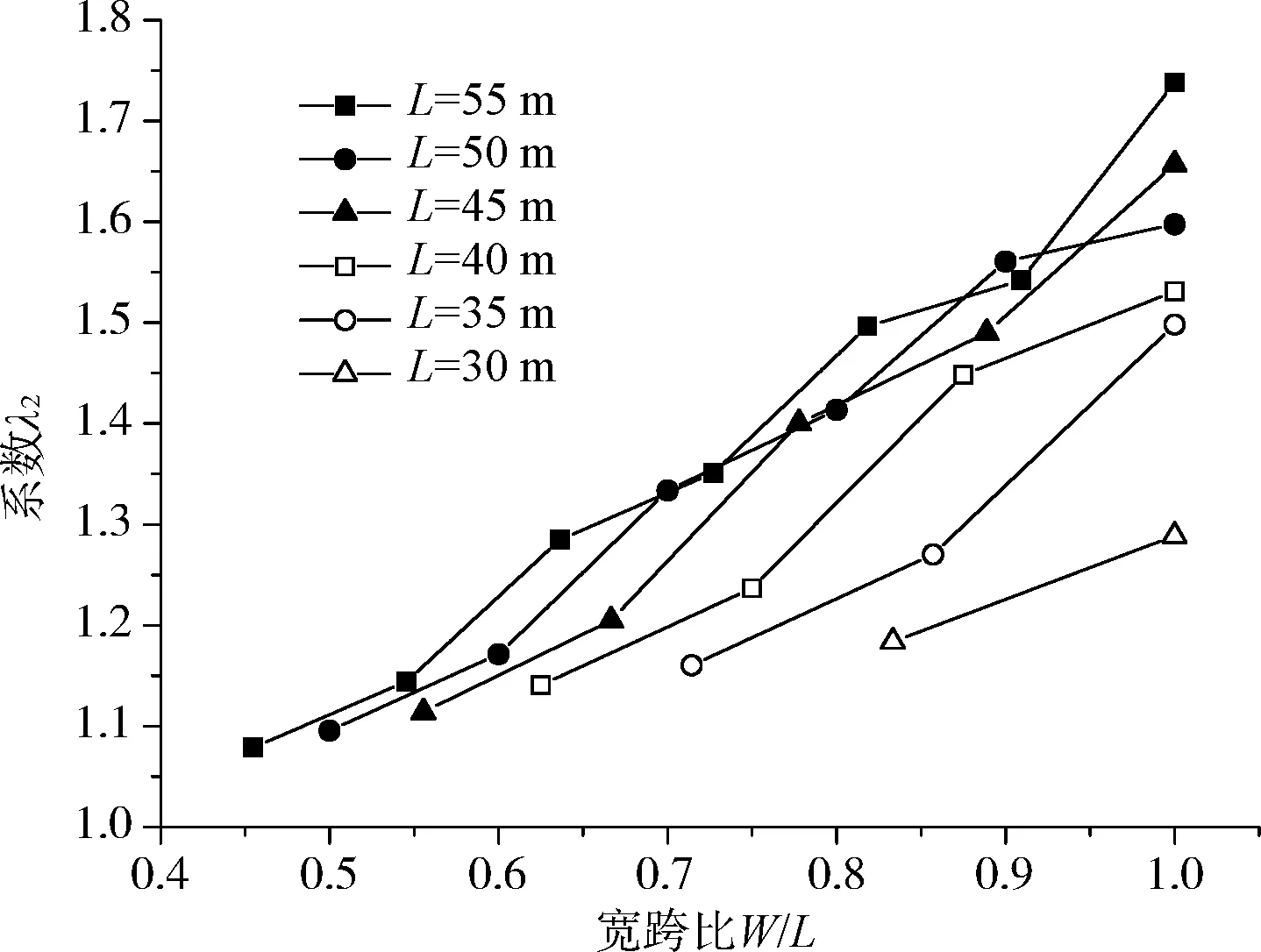
(b) 不均匀系数λ2

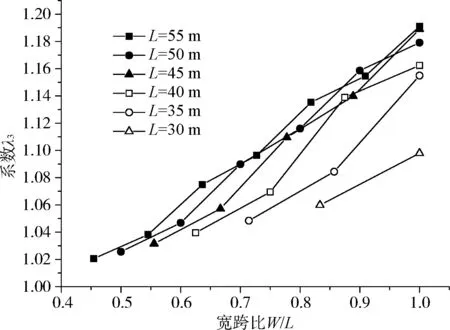
(c) 不均匀系数λ3

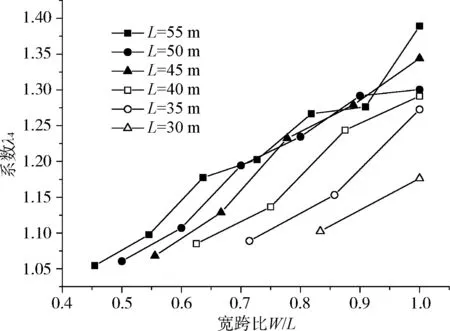
(d) 不均匀系数λ4

计算结果表明，不同跨度、不同宽跨比所对应的空间效应分布具有以下特点：

(1) 跨度相同，各腹板内力不均匀系数随宽跨比增加而增加。

(2) 宽跨比相同，各腹板内力不均匀系数随桥梁跨度的增加而增加。

(3) 边跨跨中正弯矩不均匀系数λ3<墩顶负弯矩不均匀系数λ1<中跨跨中正弯矩不均匀系数λ2；墩顶负弯矩不均匀系数λ1与剪力不均匀系数λ4基本一致。

在设计中，通常取经验值1.15作为偏载增大系数以控制箱梁腹板内力不均匀系数带来的结构安全隐患，但从上述计算结果可知，随着宽跨比的增加，各内力分布不均匀系数已远远大于1.15。因此，对于宽跨比较大且横向少约束体系的桥梁而言，这一取值显然是不安全的。

本文将不均匀系数等于1.15时所对应的宽跨比定义为临界宽跨比，图2为不同跨度桥梁所对应的临界宽跨比。

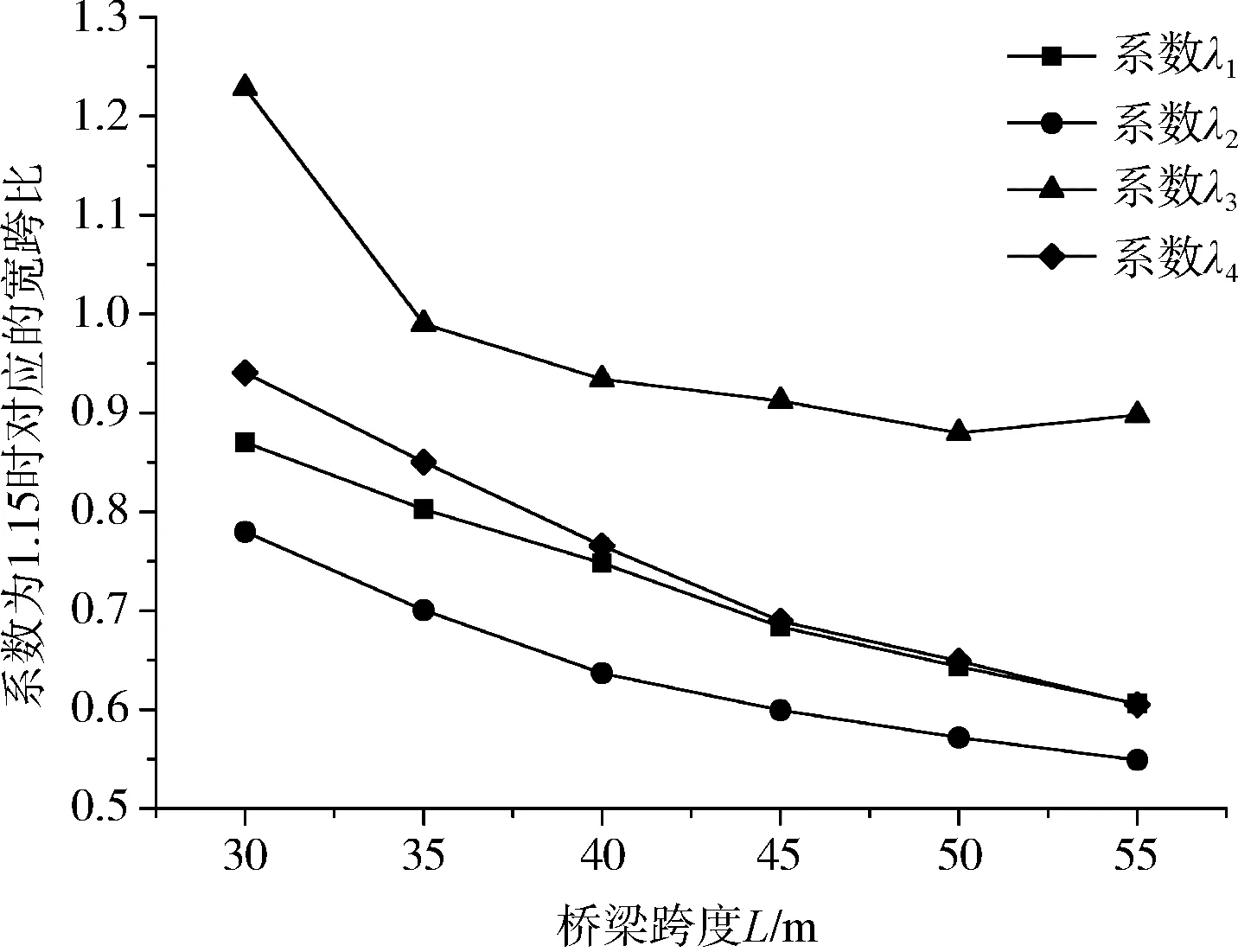
图2 不同跨度桥梁临界宽跨比

与前述空间效应分布特点不同的是，临界宽跨比随跨度的增加而减小，且四个不均匀系数以中跨跨中正弯矩不均匀系数临界宽跨比为最小，因此，建议以其对应的临界宽跨比作为结构设计是否需要考虑箱梁空间效应的判定标准。例如，对于跨度为45 m的等截面连续梁桥而言，当其宽跨比W/L≥0.6时，结构计算时应采用梁格法分别计算各腹板内力情况，反之，则可以采用单梁模型进行计算和设计。

2 工程案例分析

2.1 总体设计

本文案例工程位于四川省泸州市城市环线快速路上，是南北向主通道的重点节点工程。该工程近期规划为双向八车道，远期规划改造为双向轨道交通+双向六车道。其南引桥为(35+3×45)m四跨预应力混凝土连续梁，桥幅总宽度为41.08～49 m，箱梁截面采用流线型分离式双箱，设置墩顶横梁联系。为满足其景观定位的需求，该桥断面横向均仅设两个桥墩提供竖向约束。南引桥总体布置如图3所示。

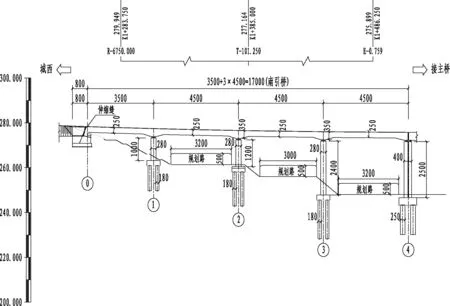
(a) 立面布置

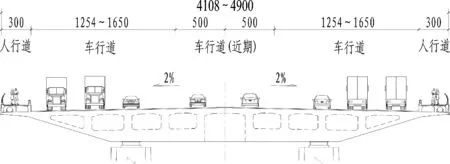
(b) 横断面近期布置

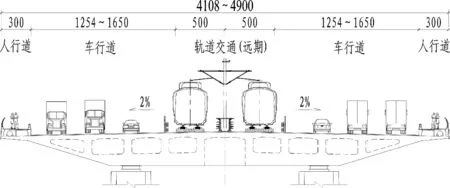
(c) 横断面远期布置

2.2 构造设计

南引桥主梁采用流线型分离式双箱截面形式，桥幅中心线处桥面板及各墩横梁设置宽度为1 m的混凝土后浇带。

主梁在桥幅中心线处，高2.5 m，在中横梁及过渡墩横梁处加高至3.5 m，以适应少支承的横梁受力需要，其横梁宽度均为3.0 m，两侧设置4.0 m长梁高渐变段。

左右两幅主梁同为单箱四室截面，顶底均设置2.0%横坡，标准断面顶板厚25 cm，底板厚22 cm，腹板厚50 cm；箱梁除最外侧的箱室宽度保持一致外，其余箱室的腹板间距随着桥面宽度变化而变化。

2.3 空间效应分析

南引桥最宽桥面处宽跨比W/L达到了1.09，远大于前文所述的临界宽跨比0.6，其结构受力空间效应显著，因此，应采用空间梁格法对其受力情况进行分析和设计。梁格划分及编号如图4所示。

图4梁格划分及编号示意

各腹板恒载作用下跨中正弯矩和墩顶负弯矩内力分布如图5～6所示。

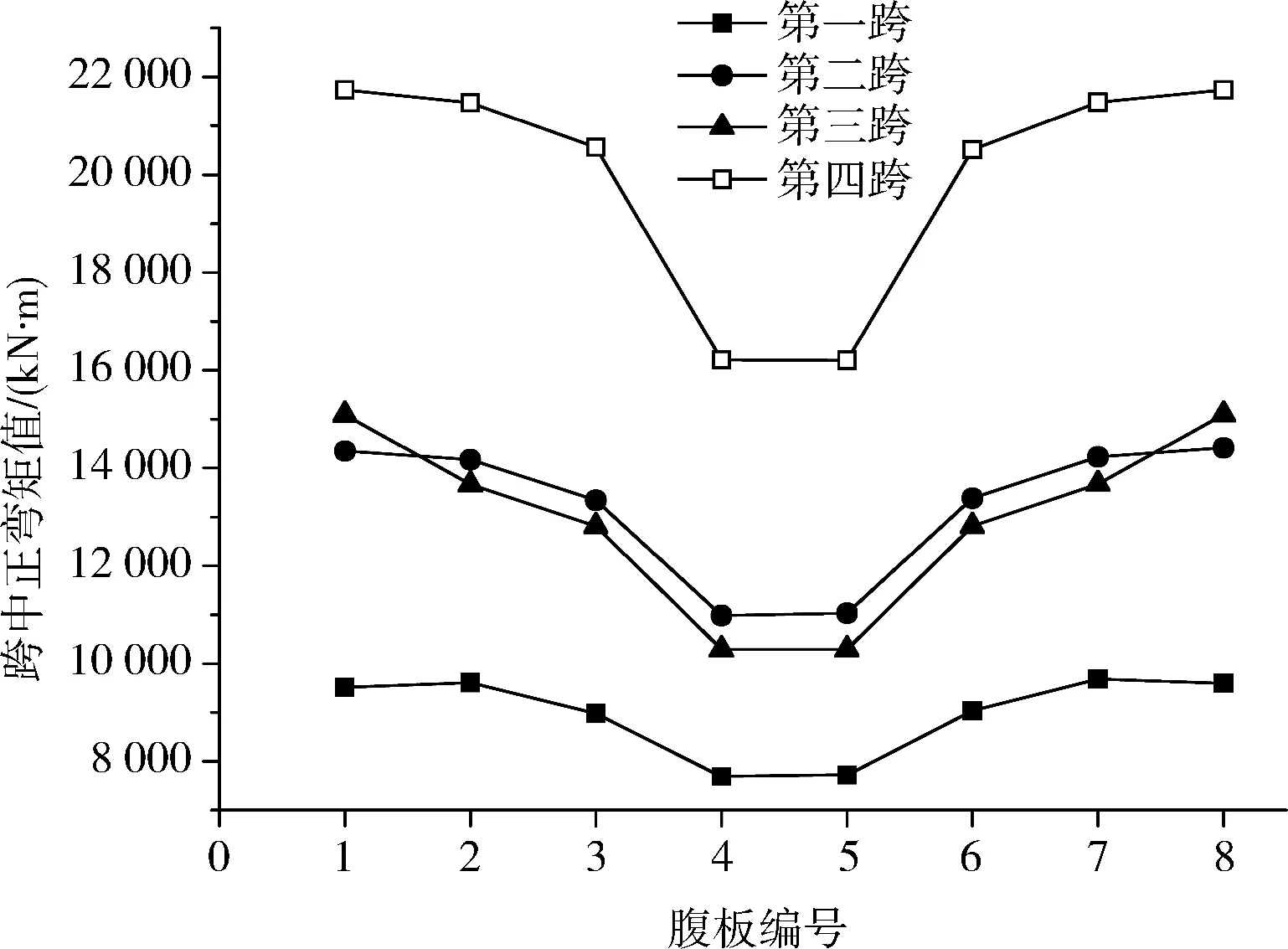
图5 各腹板各跨中正弯矩分布

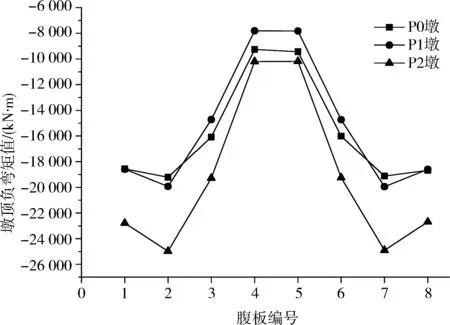
图6 各腹板各墩顶负弯矩分布

由图5～6可知，靠近桥幅中心线的腹板无论跨中正弯矩还是墩顶负弯矩，均明显小于边腹板对应的内力值，这是由于越靠近桥幅中心线的腹板受到其他腹板的约束作用越强，变形受到的限制也越大，相应内力也就越小；而边腹板一侧为自由边，受到的约束作用小，对应结构变形及内力均较大。

同时，通过计算得出各腹板恒载作用下跨中正弯矩不均匀系数在1.25～1.375范围内，而墩顶负弯矩不均匀系数在2.0～2.5范围内，显著大于跨中正弯矩不均匀系数。这是由于南引桥为分离式双箱，仅在墩顶位置设置两幅间联系横梁，且由于横向约束少，横梁悬臂大而几乎不存在正弯矩，横梁变形呈现出悬臂梁的特征，对靠近桥幅中心处的腹板相当于施加了一个向上的强制位移作用，使得其对应的内力值显著小于边腹板，从而加大了墩顶负弯矩的不均匀系数；结构跨中位置未设置横隔板，两幅箱梁仅靠顶板联系，相互约束作用不强，而墩顶横梁对整体的约束沿纵向分布至跨中截面已大幅减小，对于跨中正弯矩不均匀系数而言，其宽跨比理论上更接近于单幅箱梁宽度与桥跨的比值，约为0.54，因此，计算所得的跨中不均匀系数相对较小。沿桥跨方向各截面恒载作用下的弯矩不均匀系数如图7所示。

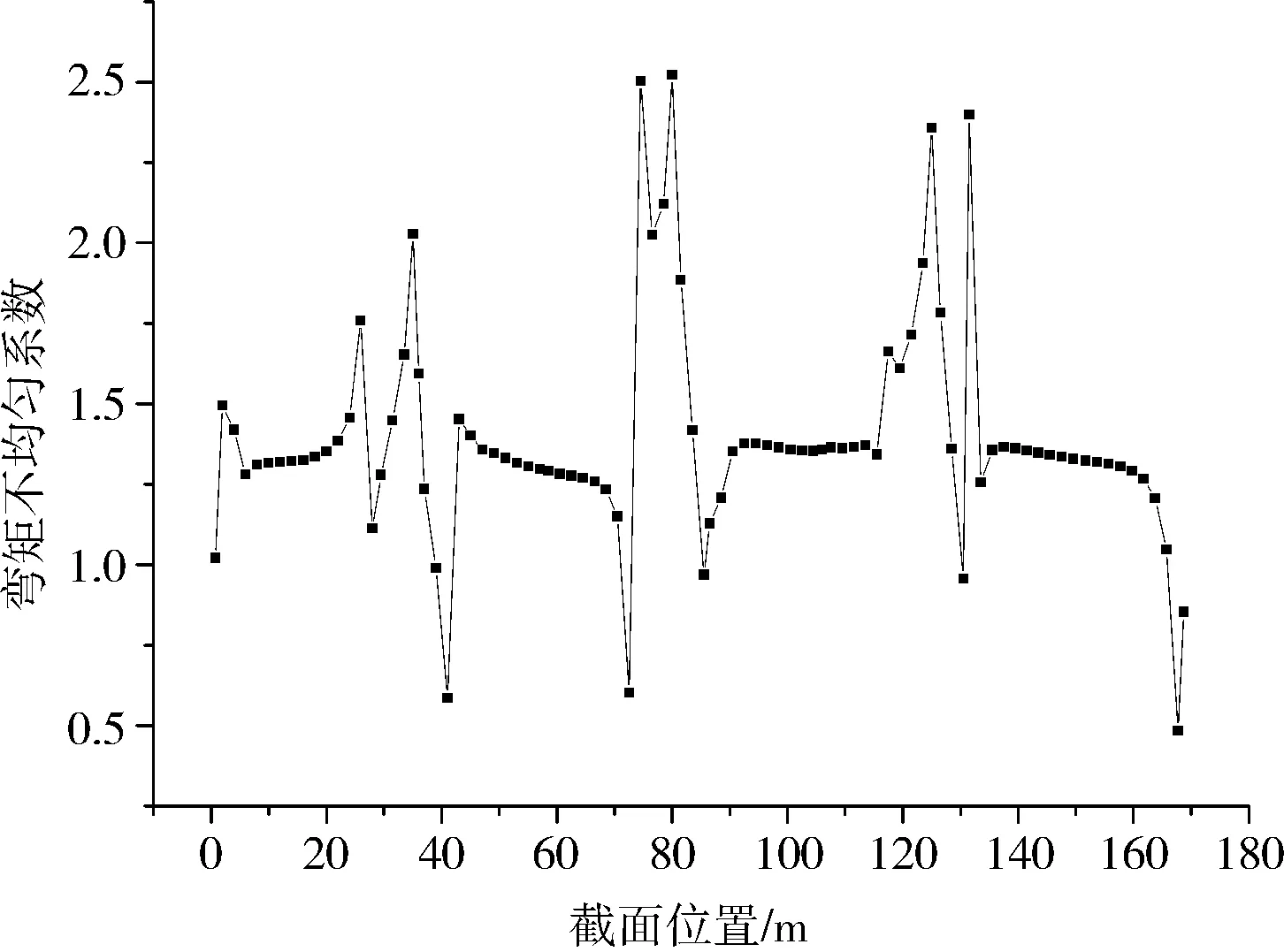
图7 恒载作用下沿跨度方向弯矩不均匀系数

由图7可知，靠近墩顶附近个别截面的不均匀系数小于1，这是由于此类截面均位于各腹板转弯点附近，弯矩绝对值很小，所计算的不均匀系数不具有参考价值。此类不正常点数量很少，表明虽然结构本身空间效应显著，但各腹板正负弯矩转弯特征点仍几乎一致。

南引桥近期双向八车道活载包络最大跨中正弯矩不均匀系数约为1.6，最小约为1.1；远期双线轨道+双向六车道活载包络最大跨中正弯矩不均匀系数约为1.2，最小约为1.1。由于轨道位于桥幅中心线附近，轮轨直接作用于4#、5#腹板，增加了其内力值，从而减小了不均匀系数，因此，近远期弯矩包络最大工况下，二者不均匀系数相差较大。

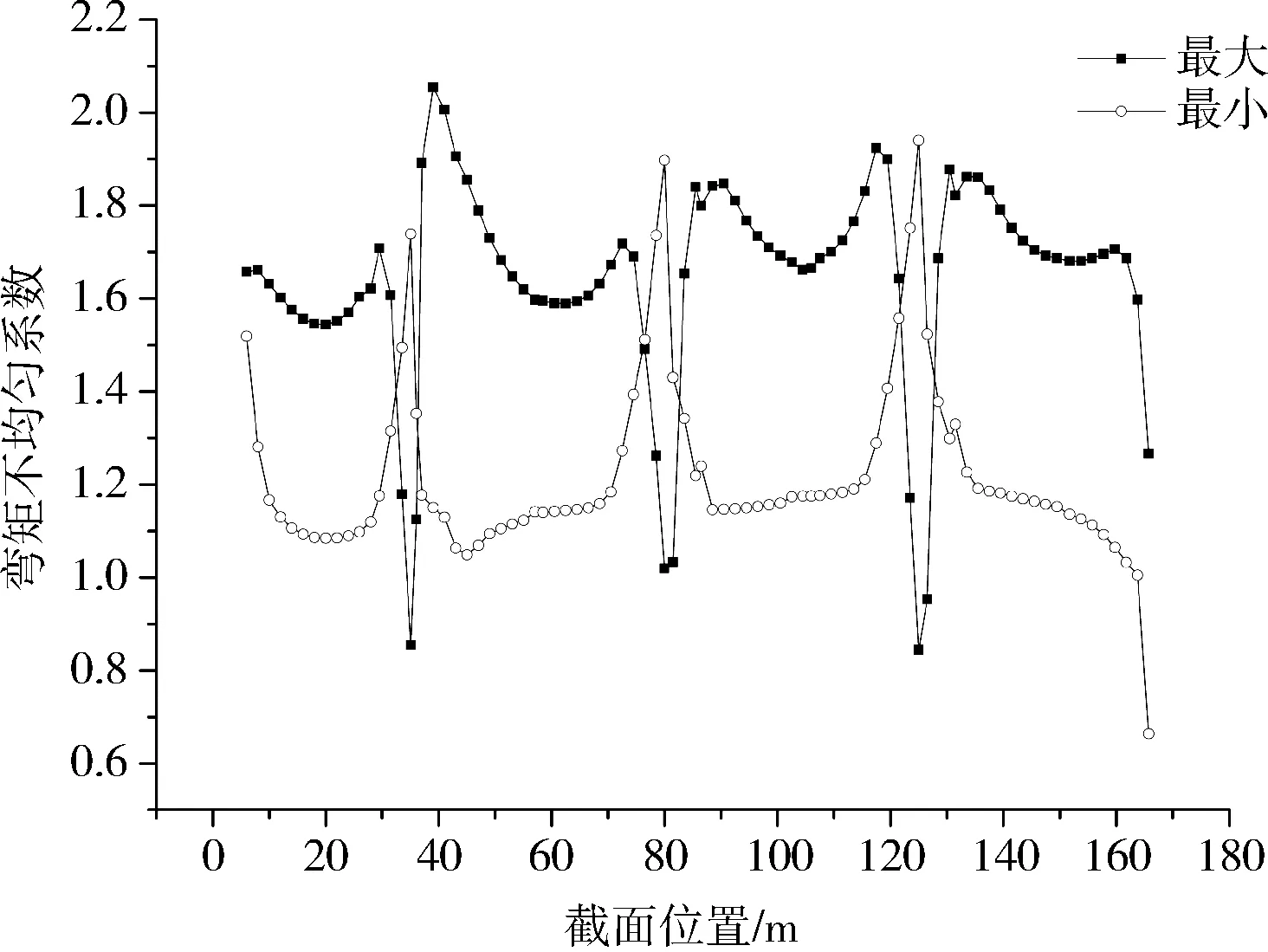
图8 近期车道荷载下沿跨度方向弯矩不均匀系数包络

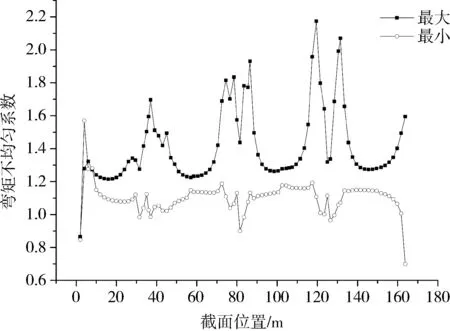
图9 远期车道+轨道荷载下沿跨度方向弯矩不均匀系数包络

3 结论

本文对30 m、35 m、40 m、45 m、50 m和55 m等6种跨度、桥宽分别对应为[25,L] (步长5 m)的三跨等截面连续梁进行计算分析，针对墩顶负弯矩、中跨跨中正弯矩、边跨跨中正弯矩和墩顶剪力等四个不均匀系数开展了研究，研究结果表明：

(1) 各内力不均匀系数随宽跨比和结构跨度的增加而增加。

(2) 临界宽跨比可以作为箱梁设计选用计算方法的重要依据，其并非固定不变而是随着跨度的增加而减小。

同时，对南引桥横向仅设两个支承约束且宽跨比大于1的超宽箱梁进行了计算，研究其结构在恒载、近远期活载作用下内力空间效应,结果表明：

(1) 因越靠近桥幅中心线的腹板受到其他腹板的约束作用越强，变形受到的限制也越大，故各工况下其跨中正弯矩和墩顶负弯矩均明显小于边腹板对应的内力值。

(2) 各腹板恒载作用下跨中正弯矩不均匀系数在1.25～1.375范围内，而墩顶负弯矩不均匀系数在2.0～2.5范围内，后者显著大于前者。

(3) 梁体转弯点附近个别截面弯矩绝对值很小，所计算的不均匀系数不具备参考价值。同时，虽然其结构本身空间效应显著，但各腹板转弯点特征基本一致。