桥梁位移影响线提取方法及其精度分析

徐 剑

(苏交科集团股份有限公司，南京 210019)

桥梁服役期间，受材料劣化、荷载作用、环境激励等内外部因素的共同作用，不可避免地产生不同程度的损伤，随着损伤的不断累积，最终可能导致桥梁结构失效，造成重大财产损失[1]。对桥梁结构进行评估，判定其服役状态，建立预警机制可以有效避免此类事故的发生。

目前，桥梁结构状态的评估方法主要有两种：实桥荷载试验与健康监测系统。实桥荷载试验多适用于中小跨径桥梁，常以承载能力为基础进行结构安全性能评估[2-5]。该方法的评定结果较为可靠，但实时性差，常以半年或一年为周期，且桥梁运营期间每个检查周期都要组织人员进行检查，后期成本高。健康监测系统因其前期成本较高，目前多被应用于大跨桥梁，该系统运用高精度传感器与现代通信技术实时获取结构状态参数，并基于信息处理技术实时评定结构安全状态，具有时效性好、后期投入小、智能化、操作简便等显著优势。利用健康监测系统评定桥梁结构的安全状态，将此系统从大跨径桥梁向中小跨径桥梁推广，将是未来的发展方向与研究热点，其中，通过影响线进行模型修正和损伤识别的方法具有广阔的应用前景。

影响线指结构某一截面或位置处某种受力效果(内力、位移或支反力)随荷载作用位置变化的函数曲线[6]。它是结构在不同位置处受荷载作用引起的静载响应，但在实际操作中，健康监测系统采集到的影响线均为实桥移动荷载引起的结构响应，其受车辆动载效应的影响不可忽略。关于桥梁位移影响线识别，国内外专家已经进行了广泛的探索。OBRIEN E J等[7]较早提出了基于测量信息反演计算影响线的思路；LENG S S[8]进一步提出了基于最大似然估计的影响线识别方法；CHEN Z W等[9]基于实测的移动火车信息和关键构件应变响应，采用Tikhonov正则化方法识别大跨悬索桥影响线；SUN S W等[10]提出引入桥梁有限元模型辅助影响线识别的方法，但却增加了分析工作量及不确定性；丁幼亮等[11]提出了一种基于FIR凯赛窗滤波器方法的应变动力系数测定方法，对位移影响线的静力识别具有一定参考价值；王宁波[12]等基于桥梁动力响应，采用多项式拟合方法实现了对桥梁应变影响线的提取。以上研究成果虽有一定的参考价值，但并未形成普遍认可的能够准确高效地识别桥梁位移影响线的方法。有鉴于此，本文提出了一种基于dbN小波变换算法[13]的影响线识别方法，为相关研究提供了一种新的思路。

1 移动荷载下的桥梁位移影响线提取

车辆的动载效应属于典型的车桥耦合问题。车辆与桥梁之间的作用力为时变力，具有随时间变化的特性[14]。因荷载是移动的，且车辆本身也是一个具有质量的振动体系，从而使车桥耦合系统的动力特征随荷载位置的移动而不断变化。

车桥耦合的解析方法可通过车、桥两子系统间的分离迭代来实现，其运动方程如式(1)～(2)所示。

(1)

(2)

式中，Fbg和Fvg为作用在桥梁和车辆上且与其运动与否并无关联的荷载；Fvb和Fbv为桥车间的相互作用力。

对于车桥系统，可分别对桥梁和车辆的运动方程进行求解，通过分离迭代来满足车桥两子系统间的几何、力学耦合关系。可以通过数值法，采用ANSYS瞬态动力学[15]求解，将桥梁结构沿跨径方向离散为若干节点，通过改变荷载作用的节点位置实现对移动荷载的模拟施加[16]，如图1所示。每一荷载步内，按静力求解得到的跨中节点位移时程曲线即为标准静力影响线；每一荷载步内打开瞬态效应，循环加载求解的结果即为考虑桥梁动力特性与车辆动载效应的动力影响线。

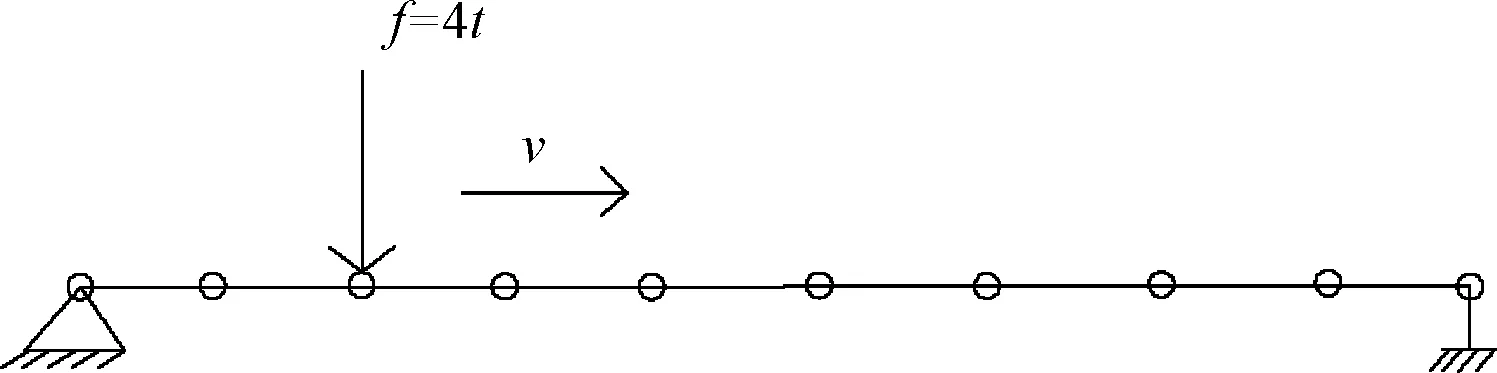
图1 移动荷载法示意

采用时程分析方法建立20 m跨径简支梁模型，分别提取静载跨中挠度时程与动载跨中挠度时程曲线，将时程曲线横坐标换算为荷载作用位置，可得静载与动载情况下的影响线，静载影响线与不同速度下动载影响线的对比如图2所示。由图2可知，静载影响线为理想光滑反抛物线型曲线，计入动载影响后，整体仍保持为反抛物线型曲线，但各条动载曲线在局部均存在波动，且最大偏离出现在中跨位置。这是由于动载曲线考虑了动载影响，即该曲线耦合了静载影响及结构对于冲击荷载的响应等两方面的因素。动载曲线的规律性还表现在速度越大，局部波动的幅值与周期越大。因此，选取适当的方法，排除不同速度下动载引起的局部波动是进行静力影响线提取的关键。

图2 静载与动载影响线对比

2 基于dbN方法的桥梁位移影响线提取

排除车辆动载效应引起的影响线局部波动，还原真实的挠度最值，是进行静力影响线识别的本质。车辆动载效应的剔除问题与信号处理中的降噪问题具有一定的相似性，目前最常用的方法主要有滤波法和小波变换法。滤波法指采用无限脉冲响应滤波器IIR、有限脉冲响应滤波器FIR、维也纳滤波器或卡尔曼滤波器等滤波器材进行滤波的方法。小波变换法即对小波变换进行分辨、分析，根据噪声与信号在不同频带上的小波分解系数具有不同强度分布的特点，将各频带上噪音对应的小波系数去除，保留原始信号的小波分解系数，然后对处理后的系数进行小波系数重构，从而得到去噪后的信号。常见的小波包括：Haar小波、Daubechies(dbN)小波系、Biorthogonal小波系、Coiflet(coifN)小波系和Morlet(morl)小波系等。

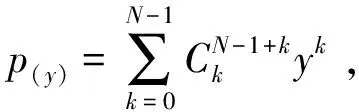
(3)

(4)

式中，ω为频率；h为转换函数。

3 误差指标的建立

为定量描述dbN小波变换后提取的影响线与标准静载影响线的接近程度，此处引入误差指标Er，Er为每个荷载作用点处两者差值的平方和。考虑到现实中极值点的数值往往更受关注，故对上述各点差值的平方进行加权，即可定量表征二者的接近程度。其中，误差指标Er的计算公式为：

(5)

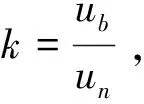
误差指标Er可以衡量dbN小波变换法对影响线的识别效果，Er值越小，表示经过小波变换后得到的结果越接近于标准静载影响线，识别效果越好。

4 dbN法提取静载影响线的效果及其适用性

分别计算简支梁桥在30 km/h、60 km/h、90 km/h 等不同速度下跨中挠度的时程曲线，将横坐标置换成荷载作用位置，然后使用dbN法进行静力影响线提取，对比标准静载影响线，结果如图3～5所示。

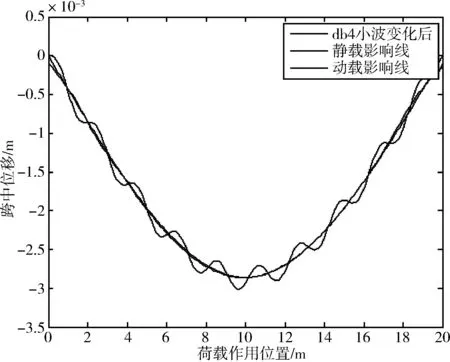
图3 简支梁v=30 km/h动载影响线小波db4识别结果

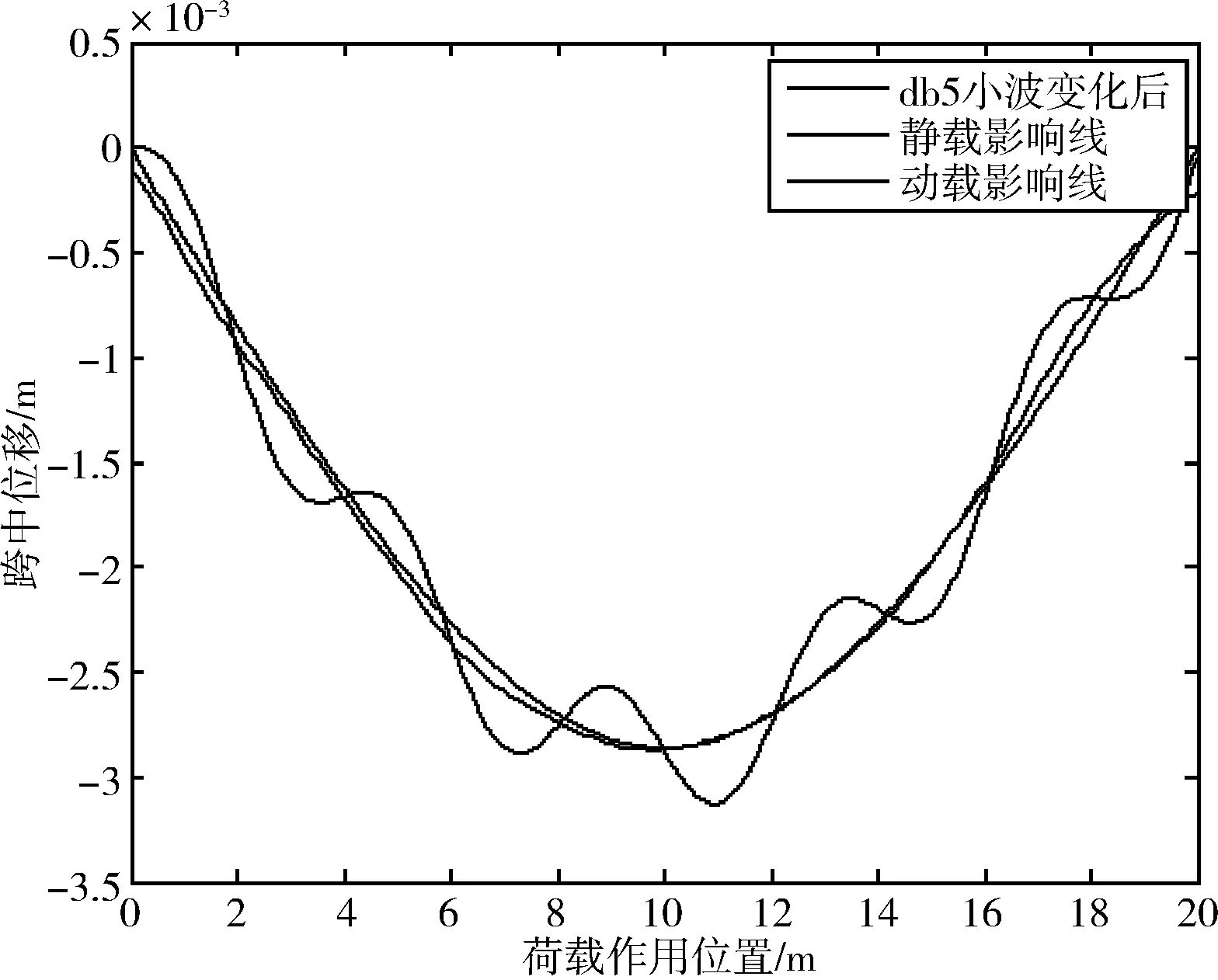
图4 简支梁v=60 km/h动载影响线小波db5识别结果

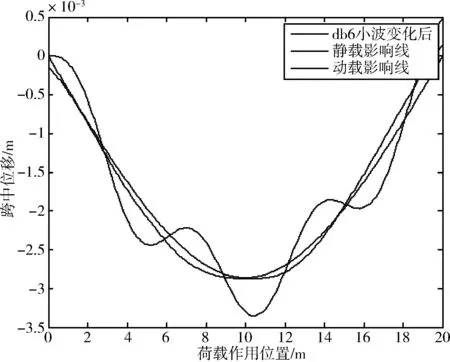
图5 简支梁v=90 km/h动载影响线小波db6识别结果

由图3～5可知，基于动载时程曲线，使用dbN法进行静力影响线提取后得到的曲线与标准静态影响线的吻合度较好，说明此方法可有效过滤掉动载效应引起的影响线局部波动。三种速度下，经dbN法提取到的影响线最值与标准静态加载的影响线几乎重合，表明该方法可有效还原跨中挠度最值。通常情况下，位移影响线反应的挠度最值更具参考价值。三种速度下，对比标准静态影响线、动载影响线与dbN法提取到的影响线的挠度最值，结果如表1所示。

表1 简支梁不同速度情况下影响线最值对比

由表1可知，采用dbN法提取到的影响线挠度最值对标准静态影响线挠度最值的还原度很高，在误差精度范围内，二者完全一致。在此基础上，分别计算dbN法提取的影响线与标准静态影响线的误差指标，可得三种速度下Er值分别为7.34、10.52和33.03。Er值反映了dbN法提取的影响线与标准静态影响线的绝对接近程度，当Er≤30时，采用dbN法基于动载时程曲线提取到的曲线与标准静态曲线有着较好的吻合性。当v=90 km/h时，误差指标Er值为33.03，相对于v=30 km/h和v=60 km/h情况下的误差指标值较大，但结合图5可知，导致该误差指标值偏大的主要原因在于该种速度下加载导致的动载效应更为明显，动载效应引起的影响线局部波动的幅值和周期相对于v=30 km/h和v=60 km/h时更加显著。综合对比动载效应影响线与标准静载影响线可知，经提取后得到的影响线不存在明显局部波动，最值与标准静载影响线吻合较好。不同速度移动荷载下，基于动载效应跨中挠度时程曲线经dbN法提取到的简支梁静载影响线效果良好、结论合理。

为进一步探索该方法的适用性，使用该方法进行简支梁双轴加载、连续梁双轴加载和连续刚构桥双轴加载等不同桥型、不同加载方式下的静力影响线提取。其中，简支梁跨径为20 m，双轴加载的轴距为2.3 m；连续梁跨径布置为20 m+30 m+20 m，双轴加载的轴距为2.3 m；连续刚构桥跨径布置为30 m+50 m+30 m，双轴加载轴距为2.5 m。选取适当的dbN参数，针对上述不同加载方式下的动载时程曲线进行影响线提取，并计算各种情况下的误差参数Er，结果如图6～7所示。

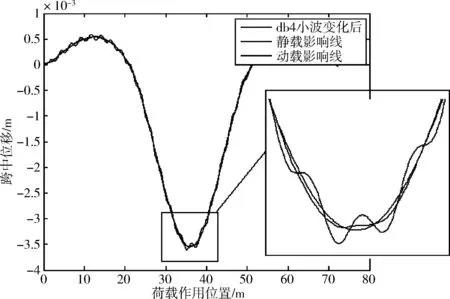
图6 连续梁桥v=40km/h 动载影响线db4小波变换影响线提取结果

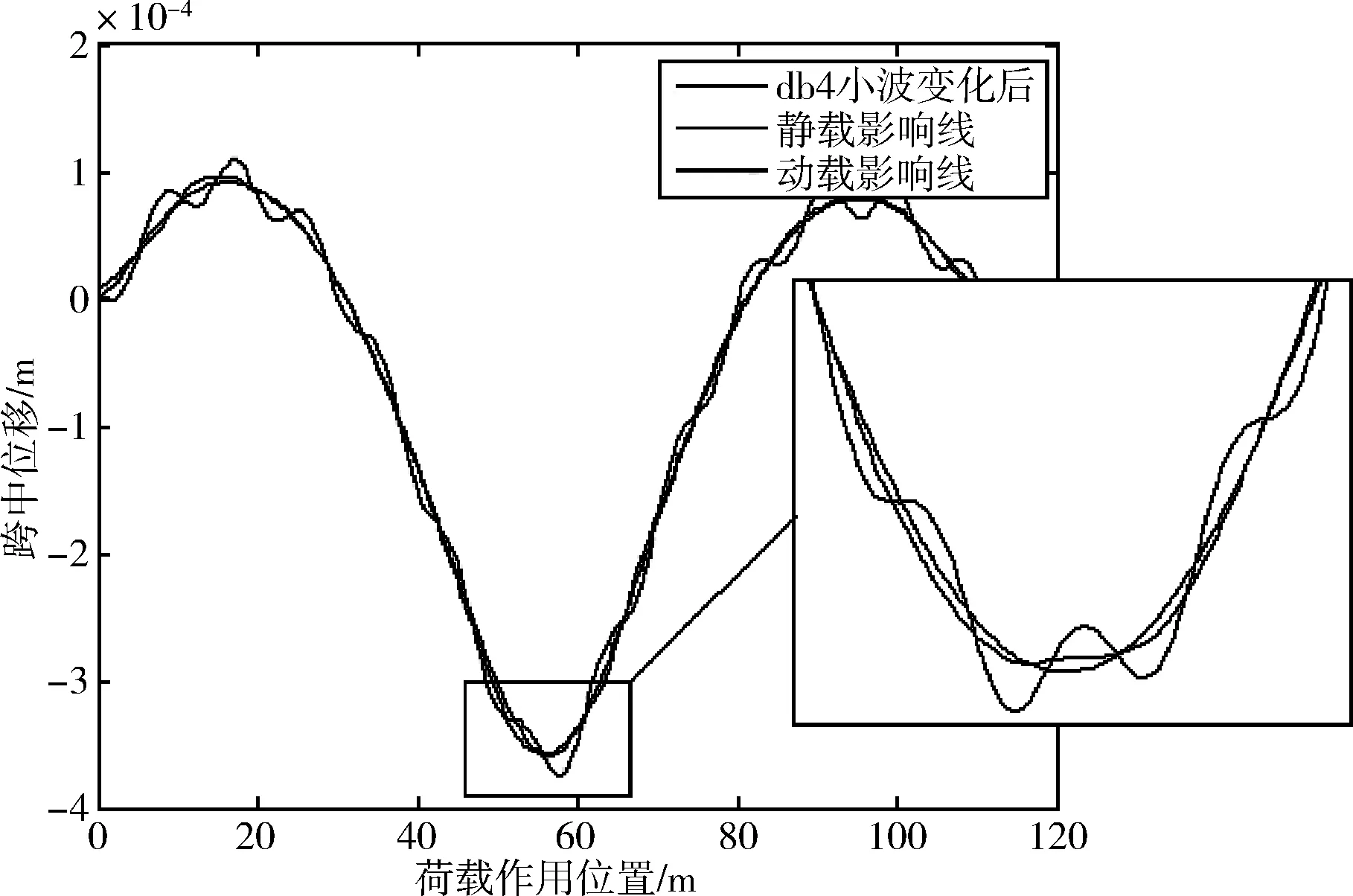
图7 刚构桥v=100 km/h动载影响线db4小波变换影响线提取结果

由图6～7可知，对于连续梁桥与连续刚构桥，采用dbN算法依然可以有效地过滤掉动载引起的局部波动，使提取到的影响线平滑，且与标准静态加载影响线吻合良好。从跨中位置的局部放大图可知，采用dbN算法提取后，对原动载影响线起到了明显的削峰作用，有效地还原了静载影响线最值。不同桥型和不同速度下，采用dbN算法提取到的静载影响线与标准静载影响线的对比结果与以上规律一致，不再一一列举。

根据以上结论，计算不同加载方式与加载速度下的误差参数，如表2所示。

由表2可知，不同加载方式和加载速度下，dbN法提取到的影响线与标准静态影响线的误差参数均小于35，且大部分不高于10，表明不同加载方式和加载速度下，dbN法提取到的影响线与标准静态影响线吻合较好，其对简支梁桥、连续梁桥及连续刚构桥均具有良好的适用性。

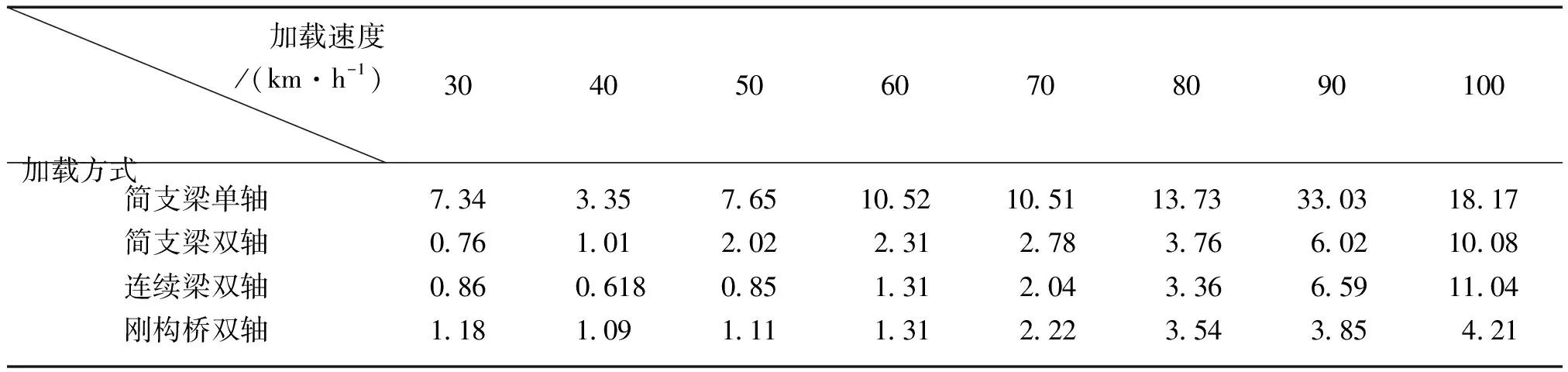
表2 不同加载方式与加载速度下dbN法提取影响线与标准静载影响线误差参数

5 结论

(1) 基于考虑动载效应的桥梁跨中动载时程曲线，采用dbN小波变换法提取桥梁静载影响线，为桥梁健康监测过程中过滤车辆动载效应以识别静载影响线问题提供了一种新的方法。

(2) 建立了一种用于评价所得影响线与标准静态影响线吻合程度的误差指标，该误差指标考虑了两者的绝对误差，并计入了不同点位处挠度差值的权重，使其更加具备工程实用意义。

(3) 基于不同加载方式和加载速度下的挠度时程曲线，提取了桥梁位移影响线，并计算了其与标准静载影响线的误差标准值Er，验证了该方法对于简支梁桥、连续梁桥和连续刚构桥梁的位移影响线提取均具有较高的识别精度和良好的适用性。

综上所述，dbN小波变换法对于桥梁位移影响线的识别提取具有良好的适用性，可为类似工程应用提供参考。