独立样本t检验的Excel和SPSS分析

高艺祥，杨民红，李兰会

（1.河北农业大学动物医学院，河北 保定 071001；2.河北省新乐市农林畜牧局农业行政综合执法大队，河北 新乐050700；3.河北农业大学动物科技学院，河北 保定 071001）

医学统计学是临床医学、基础医学、公共卫生学和医疗卫生服务研究的一门基础学科［1］，研究对象主要是医学中具有不确定性结果的事物，其主要作用是通过数据的偶然性揭示内在的规律性［2］。统计分析的要点是正确地选用统计分析方法，并结合专业知识做出科学的结论。科学的任务就在于，从看起来错综复杂的偶然性中揭露出潜在的必然性，即事物的客观规律性。这种客观规律性是在大量现象中发现的，例如临床要观察某种疗法对某病的疗效时，如果观察的病人较少，便不容易正确判断该疗法对某病是否有效；但当观察病人的数量足够多时，就可以得出该疗法在一定程度上有效或无效的结论，因此，医学统计学是医学科学研究的重要工具。

医学统计学的内容包括：①定量数据的统计描述。主要内容包括集中趋势的统计指标：算数均数、几何均数、中位数和百分位数。变异程度的统计指标：极差、四分位数间距、方差、标准差、变异系数。②总体指标的估计。医学研究中实际观测或调查的部分个体称为样本，研究对象的全体称为总体。除用均数、率等统计指标对调查或实验结果进行描述外，更重要的是通过样本的信息，来估计总体中相应的统计指标，即参数估计。③假设检验。就是依据资料性质和所需解决的问题，先建立适当的假设，然后采用适当的检验方法。④基本的运算工具是假设检验的方法工具：U检验、t检验、方差分析和 χ2检验［3］。

1 案例分析

以马斌荣主编的医学统计学教材为例［1］，解释说明应用Excel和SPSS统计工具进行独立样本t检验的基本过程。“某项研究评估低氧环境对运动者心肌血流量的影响，将17名男性志愿者随机分为2组，分别在正常含氧环境（正常组）和低氧环境 （低氧组）中测定运动后的心肌血流量［mL/（min·g）］：正常组为 3.5、3.1、3.1、2.7、2.5、2.3、2.3、2.2、2.2 mL/（min·g）； 低氧组为 6.4、5.7、5.6、5.3、5.1、4.9、4.7、3.5 mL/（min·g）。 问 2 种环境中运动者的心肌血流量有无差异？”。

表1 Excel的F检验·双样本方差输出结果（一）

两独立样本t检验，又称成组t检验，它适用于完全随机设计的两样本均数比较，其目的是检验两样本代表的总体均数是否相等，即通过x1和推断μ1和μ2。该案例在于揭示氧气浓度不同对运动者的生理状态是否有影响，将志愿者随机分为2组，采用了完全随机的试验设计方法，通过低氧和正常环境2种环境下志愿者运动后的心肌血流量揭示氧气浓度与生理状态间是否存在关系。

2 Excel的解读

利用Excel分析操作步骤分两步，第一步是进行F检验，工具→数据分析→F检验·双样本方差，F检验的目的在于分析两样本数据的总体方差和是否相等；第二步在F检验的基础上进行t检验，推断两总体均值μ1和μ2是否相等，主要分两种情况：如果方差相等，则进行等方差假设的t检验，否则进行异方差假设的t检验［4］。

2.1 双样本方差分析

由Excel双样本方差输出结果（见表1）可知，低氧组和正常组的心肌血流量样本均值分别为5.15和2.66， 方差和分别为0.73和0.23，两样本的样本含量分别为8和9，两样本自由度分别为7和8。F检验的F检验统计量为3.22，F为两样本方差的比值，即F==0.73/0.23=3.22，F值3.22在自由度df1和df2分别为7和8的F分布下出现的单尾概率P=0.06，该概率为F值小于3.22的区间概率，即F值为0～3.22在F分布总体0～+∞中所占的百分比，由此可知，F值的概率大于0.05，不是小概率，所以认为两样本间的差异是由实验误差引起的，两总体方差和相等。同时输出结果中F单尾临界值3.50，即否定域和接受域的分界线为3.50，0～3.50的区域为接受域，F分布的右尾3.50～+∞的区域为否定域，所以F值3.22落在接受域，不能否定H0，两样本所在总体方差相等。

表2 Excel的F检验·双样本方差输出结果（二）

Excel操作过程中重新进行F检验，但变换变量1和变量2的区域，即低氧组设为变量2，正常组为变量1，输出结果见表2。

通过表1和表2的对比可知交换变量后，正常组和低氧组的平均数、方差、观测值、自由度、单尾P值都没有变化，而统计量F值和F的单尾临界值发生了改变。表2中，在自由度df1和df2分别为8和7的F分布下出现的单尾概率P=0.06，即F值为0～0.31在F分布总体0～+∞中所占的百分比为6%。表2中F单尾临界值0.29，由于变化了两个变量的位置，F值否定域改变为F分布的左尾：0～0.29，0.29～+∞ 为接受域， 所以 F 值 0.31 落在接受域，不能否定H0，两样本所在总体方差相等，因此，交换变量后并没有发生实质性的变化，最后的结论依然不变。

2.2 独立样本t检验

Excel分析工具中有等方差假设和异方差假设的两种独立样本t检验工具［5］，根据双样本方差分析结果，该例选用等方差假设的独立样本t检验，Excel输出的t检验结果见表3。根据t检验的输出结果，可以由4个统计量推断低氧组和正常组两总体均值心肌血流量是否相等，分别是单尾概率、单尾临界值、双尾概率和双尾临界值。

由表3可知，低氧组和正常组的合并方差t检验统计量：

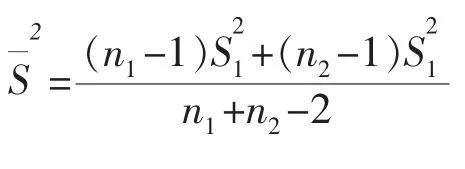
表3 Excel的等方差假设t检验输出结果

①由单尾概率推断：t值7.58在自由度为15的t分布下出现的单尾概率P=8.33×10-7，该概率为t值大于等于7.58的区间概率，即t值为7.58～∞在t分布总体-∞～+∞中所占的百分比，由此可知，t值的概率小于0.05，是小概率，拒绝H0可认为两总体均值μ1和μ2不相等。

②由单尾临界值推断：t单尾临界值1.75，即否定域和接受域的分界线为1.75，-∞～1.75的区域为接受域，1.75～+∞的区域为否定域，所以t值7.58落在拒绝域，否定H0，两样本所在总体均值不相等。

③由双尾概率推断：t值7.58在自由度为15的t分布下出现的双尾概率P=1.67×10-6，该概率为t值7.58落在该t分布总体的两个尾部的概率，即t值在-∞～-7.58和7.58～+∞2个尾部的区间概率。该概率小于0.05，根据小概率实际不可能原理拒绝H0，认为两总体均值不相等。

④根据t双尾临界值2.13，即自由度15的t分布总体中-∞～-2.13和2.13～+∞的区域为拒绝域，-2.13～2.13的区域为接受域，所以t值7.58落在拒绝域，否定H0，两样本所在总体均值不相等。

3 SPSS的解读

利用SPSS分析操作步骤为分析→比较均值→独立样本t检验，输出结果见表4。SPSS的独立样本t检验结果中的内容涵盖了Excel的双样本方差检验、两样本等方差t检验和双样本异方差t检验的结果。

SPSS的方差齐性检验方法与Excel不同，采用的Levene检验方法［6］，从输出结果的F值及其概率进行推断，概率为0.33＞0.05，所以不能否定H0：，推断两总体方差相等，所以后面采用等方差假设的t检验结果进行推断。t=-7.58，与Excel的结果完全一致，但表4中无单尾概率，只有双尾概率0.00＜0.05，也没有临界值，但推断结论与Excel完全一致，否定H0，认为μ1和μ2不相等。

表4同时给出平均值差值，即表面效应和实验误差分别为平均值差值：-=2.49和差值标准误 SX1-X2=0.33，二者的比值即 t值（公式 2），t是表面效应和实验误差（差值标准误）大小比较，如果表面效应的大小远远超出实验误差能解释的数据变异范围，即t值较大，那么表面效应就不单纯是由实验误差引起的，还有本质效应μ1-μ2起作用；反之，表面效应是由实验误差引起的，本质效应不存在。表4同时给出了本质效应的估计值，差值95%的置信区间1.79～3.20，该区间大于0，不包括零假设的μ1-μ2=0，所以推断本质效应存在，低氧组的心肌血流量高于正常组。这一研究结果提示人们锻炼身体所处的环境对身体生理状态有显著影响，因此选择舒适的外围环境是强身健体的首选。

4 分析讨论

Excel中的方差齐性检验为单侧检验，当大方差比小方差时，F值大于1，否定域位于F分布总体的右尾部；当小方差比大方差时，F值小于1，否定域位于F分布总体的左尾部。该案例调换变量1和变量2的取值后，计算得到的F值互为倒数，F临界值也互为倒数，F值出现的单尾概率不变，推断结论不发生改变。

表4 SPSS的独立样本t检验结果

根据双样本方差分析结果，即两样本所在总体方差是否相等，选择等方差和异方差假设的t检验推断两样本总体均值是否相等。等方差假设t检验进行推断估计的准确度高，如果方差不等，对计算的t值或自由度进行调整，如表4显示异方差假设的t值和自由度都进行了矫正，目的在于降低估计误差，提高估计准确度。

Excel的双样本t检验的输出结果中有单侧概率及其临界值和双侧概率及其临界值，即分别是进行单侧检验和双侧检验的推断依据。单侧和双侧检验多数情况的推断结论是一致的，但也有出现矛盾的时候，具体是按单侧还是双侧则应根据题干要求进行选择，如果分析两个处理哪个高哪个低，则选择单侧检验；如果分析两个处理是否相同或不同，则选择双侧检验。

SPSS的输出结果更为完整，虽然没有列出临界值，临界值的应用是由于过去没有计算机，直接计算概率困难，借用临界值作为标准；现在计算简单方便，计算得到统计量后，其概率可以直接得出，所以直接利用统计量的概率即可进行推断。另外，SPSS给出了表面效应、实验误差的大小，以及本质效应的估计值，也可以由本质效应进行推断。医用生物统计课程性质的特殊性决定了学习方式的灵活多样性，生物统计学的生命在于应用，统计的价值和魅力只有在解决实际问题的应用中才能得以体现［7-8］。学生在上机实验时结合SPSS和Excel程序运行统计分析、习题课等多种学习方式［9］可以有效提高其学习兴趣，并能强化学习效果。