基于阶频谱相关组合切片的滚动轴承故障特征提取

夏均忠， 汪治安， 陈成法， 于明奇， 吕麒鹏

(军事交通学院 军用车辆工程技术研究中心，天津 300161)

滚动轴承广泛分布于各类机械设备中，其技术状态直接影响设备的工作性能，轴承的失效容易引起生产事故并有可能带来巨大的经济损失，因此，有必要对滚动轴承进行故障诊断[1]。

循环平稳理论是滚动轴承故障诊断的重要理论[2]。传统的循环平稳分析主要通过二阶循环统计量中的谱相关密度及其归一化的谱相干函数来提取滚动轴承故障特征[3-4]。Girondin等[5]将循环自相关、小波分析与支持向量机相结合用于滚动轴承特征提取。Antoni等[6]在短时傅里叶变换的基础上提出了快速谱相关算法，在提高谱相关估计速率的同时，保证了其估计质量。但循环谱相关密度并不能有效分析变转速工况下的滚动轴承故障信号[7]。

Abboud等[8-11]在循环平稳理论的基础上，提出了角度/时间循环平稳(Angle/Time Cyclostationary, AT-CS)，用阶频谱相关(Order-frequency Spectral Correlation, OFSC)提取变转速条件下的机械故障特征，但是该方法的计算量大，不能满足在线监测的要求。

由于特征循环频率处的谱相关密度切片能量明显高于其他位置的能量分布，因此可以利用特征循环频率组对应的组合切片提取滚动轴承故障特征，这种方法称为谱相关密度组合切片[12-13]。明阳等[14-15]将谱相关密度组合切片应用于滚动轴承故障诊断，具有较高的计算效率和估计精度。

通过以上分析，本文在阶频谱相关的基础上，应用组合切片思想，提出基于阶频谱相关组合切片的滚动轴承故障特征提取方法，仅计算信号的阶频谱相关中与滚动轴承故障相关的特征阶次，减少阶频谱相关计算量，通过阶频谱相关组合切片能量分布提取滚动轴承故障特征，兼顾计算效率和估计质量。通过仿真和实验验证所提方法的有效性和优越性。

1 阶频谱相关及其估计

1.1 基于AT-CS的阶频谱相关

角度/时间循环平稳信号是指这样一类信号：由于机械的旋转对称结构，运行过程中的冲击产生的信号在角域具有周期性，在时域为平稳随机过程。

角度/时间循环平稳信号的表达式为：

(1)

式中：β表示循环阶；t和θ分别为时间和角度变量，其满足下列关系：

(2)

式中：ω(t)为瞬时角速度。

阶频谱相关为角度/时间循环平稳的二阶循环统计量，它是AT-CS信号角频瞬时功率谱(Angle-frequency Instantaneous Power Spectrum, AF-IPS)S2X(f,θ)的傅里叶系数：

(3)

(4)

对于AT-CS信号，当信号的长度足够长时，其阶频谱相关具有如下性质：

(5)

阶频谱相关是谱频率f和循环阶α的函数，其横坐标是一系列离散的αi，纵坐标是连续的谱线。在循环阶α=0处，阶频谱相关等价于信号的角频瞬时功率谱；在循环阶α=β处，会形成幅值明显的谱线；在其他α处阶频谱相关函数为零。

根据角度/时间循环平稳信号的定义可知，变转速条件下滚动轴承故障振动信号具有角度/时间循环平稳特性，其阶频谱相关函数在故障特征对应的循环阶处会呈现明显的谱线，因而可以用阶频谱相关提取变转速条件下滚动轴承故障特征。

1.2 阶频谱相关的估计方法

理论上AT-CS信号的阶频谱相关是连续的量，但在工程应用中只能采集到离散的振动加速度信号，不能直接用于阶频谱相关分析。在离散的条件下，一般用循环周期图法来估计阶频谱相关。循环周期图估计方法具有良好的频率分辨率和统计特性，通过合理的参数设置，可以获得较高频率分辨率和无偏估计性。

基于循环周期图的阶频谱相关是通过信号互功率谱的Welch估计实现，其表达式为：

(6)

(7)

影响阶频谱相关估计算法计算效率的因素主要有：信号长度L、窗口宽度N、重叠率R、循环遍历长度αL和循环阶次分辨率Δαmin。在其他因素一定的条件下，遍历长度越长，分辨率越高(即αΔmin的值越小)，计算时间越长。

2 阶频谱相关组合切片

当滚动轴承发生故障时，其振动信号的阶频谱相关能量主要分布在其故障特征阶次处，如滚动体、内圈、外圈故障阶次，以及转频和保持架转频的阶次，在其余阶次上理论上不存在能量分布。对其余阶次的阶频谱相关估计不仅没有意义，还会增加计算量。

将组合切片思想与阶频谱相关估计相结合，提出基于阶频谱相关组合切片的滚动轴承故障特征提取方法，在计算振动信号的阶频谱相关函数时，仅计算滚动轴承故障特征阶次及其附近阶次的阶频谱相关函数，其算法流程，如图1所示。

图1 阶频谱相关组合切片算法流程Fig.1 The flow chart of rolling element bearings based on combined slice of order-frequency spectral correlation

(1)根据滚动轴承的结构参数和相关公式计算不同故障部位的理论故障特征阶次αi。

(2)确定切片区间。以αi及其谐波为切片中心αT，选择合理的切片宽度Δα，保证切片区间能够充分包含理论故障特征阶次，由此确定切片区间QT=[α1-Δα/2∶α1+Δα/2,α2-Δα/2∶α2+Δα/2,α3-Δα/2∶α3+Δα/2…]。

在估计参数设置一样的条件下，阶频谱相关算法和阶频谱相关组合切片算法的计算量的比值如下：

(8)

式中：CS为阶频谱相关组合切片的计算量；COFSC为阶频谱相关方法的计算量；n为切片中心的数量；Δα为每次切片的宽度。αL,Δα,Δαmin满足如下关系：

αL≫Δα≫Δαmin

(9)

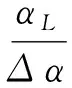
3 仿真分析

变转速条件下的滚动轴承故障信号仿真模型[16]为：

(10)

振动信号x(t)由变转速下的故障振动信号xv(t)和高斯白噪声n(t)组成。Ai表示第i次冲击对应的幅值，受到转频的调制，它与转频满足线性关系：Ai=a*vi+b；s(t)=e-βtcos(2πfnt)为故障的冲击响应；Ti为第i次冲击发生的时刻，由于速度变化不再具有周期性，但是可以通过角域周期反推得到；τi表示不同冲击之间相对的滑移。

设模拟的轴承外圈故障特征阶次为F0=4.5。同时假设轴承的转频方程为v(t)=9t+10。仿真模型设置的参数,见表1。

表1 仿真模型设置参数Tab.1 Parameters of simulated model

由上述仿真模型及设置参数得到故障轴承仿真信号的时域波形如图2所示。随着时间的推移，转频提升，振动信号的幅值逐渐增大；由于噪声的缘故，难以识别轴承故障特征。

图2 仿真信号的时域波形Fig.2 Simulated faulty bearing signal in time domain

使用阶频谱相关对其进行分析，得到的结果如图3所示。从中可以分辨出预设的滚动轴承故障特征阶次及其谐波。

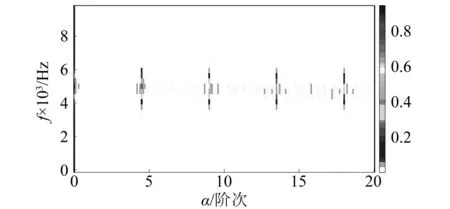
图3 仿真信号的阶频谱相关Fig.3 OFSC of simulated signal

如图4所示为应用阶频谱相关组合切片对仿真信号进行进一步分析的结果。相比于阶频谱相关，阶频谱相关组合切片干扰成分少，故障特征更加清晰。阶频谱相关的计算时间为20.72 s，阶频谱相关组合切片的计算时间为8.99 s，后者的计算时间明显快于前者。

图4 仿真信号的阶频谱相关组合切片Fig.4 Combined slice of OFSC of simulated signal

4 实验验证

实验装置主要由三相驱动电机、变频控制器、驱动轴、从动轴等组成[17]。通过变频器控制电机转频在10～20 Hz之间；采样频率为50 kHz，采样时长为21 s。

试验轴承安装在从动轴上，其主要技术参数见表2。分别在3个轴承上加工了外圈、内圈、滚动体故障，故障形状为正方形，深度为1 mm，边长为3 mm。根据表2中的技术参数计算得到滚动轴承的理论故障特征阶次，见表3。

表2 实验轴承技术参数Tab.2 The specification of tested bearings

表3 轴承理论故障特征阶次Tab.3 Bearing fault characteristics (orders)

不同故障轴承实验的转速曲线和振动信号时域波形，分别如图5和图6所示，滚动轴承的振动信号受到转频的调制，更加复杂，不能从振动信号中观察判断滚动轴承的故障类型。

计算三种技术状态轴承的阶频谱相关，结果如图7所示。在不同故障特征阶次及其谐波附近，阶频谱相关分布有幅值明显的谱线；另外，其转频阶次及其谐波处对应的阶频谱相关的幅值也较为明显。

图5 实验轴承运行转速曲线Fig.5 Speed profiles of tested bearings

图6 故障轴承振动信号时域波形Fig.6 Vibration signals of fault bearings

图7 故障轴承振动信号的阶频谱相关Fig.7 OFSC of fault bearings

图8 故障轴承振动信号的阶频谱相关组合切片Fig.8 Combined slice of OFSC of fault bearings

用阶频谱相关组合切片方法对三种技术状态轴承振动信号进行特征提取，得到的结果如图8所示。阶频谱相关组合切片可以更加清晰显示不同的故障类型，没有多余成分的干扰。

为了比较两种方法的计算效率，取信号长度为N=fs×2=100 000，分别计算两种算法的运行时间(处理器 Intel Core i7-4710MQ @ 2.50 GHz 四核，内存4GB DDR3L)，其结果见表4。阶频谱相关组合切片算法明显快于阶频谱相关算法，计算效率明显提高。

表4 不同算法的计算时间对比Tab.4 Comparison of Compute time with different algorithms min

5 结 论

(1)基于AT-CS的阶频谱相关滚动轴承特征提取方法，不需要进行角域重采样，并且具有良好的频率分辨率和抗噪性能，可以有效提取变转速工况下滚动轴承故障特征，但是阶频谱相关估计算法计算量大，不能满足在线诊断的要求。

(2)论文在阶频谱相关算法的基础上，提出了基于阶频谱相关组合切片的滚动轴承故障特征提取方法。将组合切片思想应用到阶频谱相关的估计中，降低算法的计算量，同时突出滚动轴承的故障特征，在保证估计质量的同时，提高了故障特征提取的速率，为该方法在滚动轴承的状态监测中的应用奠定了基础。