变分模态分解和同步挤压小波变换识别时变结构瞬时频率

刘景良 ， 郑锦仰， 林友勤， 邱仁辉， 骆勇鹏

( 1. 福建农林大学 交通与土木工程学院，福州 350002； 2. 福州大学 土木工程学院，福州 350108)

环境激励下的土木工程结构/构件本质上属于时变和非线性系统，其响应信号不但呈现非平稳性，同时也具有模态密集性。通常情况下，为准确识别时变结构的特征参数需对多分量响应信号进行有效分解。目前，常见的信号分解方法有经验模态分解(Empirical Mode Decomposition，EMD)[1]、局部均值分解(Local Mean Decomposition，LMD)[2]和集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)[3]等递归模式分解方法。其中，EMD与LMD都是根据信号时间尺度的局部特征对分量信号的包络线进行估计，但在估计过程中误差不断传播，分解时有可能出现模态叠混现象，故无法有效分解频率相近的信号分量。不仅如此，噪声的干扰有可能使得原始信号的非极值点变为极值点，因而信号的包络线估计会出现误差[4]。EEMD通过加入白噪声对EMD中出现的模态叠混现象进行抑制，但该方法需要进行成百上千次运算，且有可能分解出超出信号真实成分的分量个数[3]。此外，递归模式分解方法还存在端点效应等问题[5]，这给实际应用带来了不少困难。

最近，Dragomiretskiy等[6]提出一种非递归模式分解方法，即变分模态分解(Variational Mode Decomposition，VMD)。该方法通过迭代搜寻变分模型的最优解并以此确定所有分量的频率中心和带宽，从而直接从频域中分离各分量信号。截至目前，VMD已在参数识别和损伤识别等领域得到广泛应用。如Wang等[7]利用VMD成功分解了结构齿轮中的摩擦信号并准确识别了齿轮故障位置。张蒙等[8]将基于VMD和EMD的多尺度排列熵进行比较，结果表明VMD算法不仅能够克服EMD算法不能分离模态叠混信号的缺点，且分解出的分量信号在各个尺度均包含更多细节。Chen等[9]基于VMD算法和信号调制方法提出能够分解非窄带信号的VVMD算法，进一步拓宽了VMD算法的使用范围。虽然VMD不具有递归模式分解方法中的一些缺点，但其算法本身也存在一般频域分割算法无法避免的共同问题，即需要预先判断原信号中分量信号的个数[6]。分量信号数目的判别可通过频率相近原则[10-11]、粒子群优化算法[12]或是本征信号的峭度值[13]等方法来实现，但上述方法均是通过对分量个数进行试取从而得到最优值，降低了算法的整体计算效率。总而言之，VMD作为一种新的多分量信号分解方法，其算法的改进和在土木工程中的应用还十分缺乏。

VMD分解得到的分量信号通常是调幅调频信号，需要有效的时频分析方法进行分析处理。Daubechies等[14]提出的同步挤压小波变换(Synchrosqueezing Wavelet Transform，SWT)将小波变换后的时频图进行重组从而获得较高频率精度的时频曲线。刘景良等[15]将同步挤压小波变换引入土木工程领域，并研究了不同小波母函数对同步挤压小波变换的影响。汪祥莉等[16]利用同步挤压小波变换对混沌背景下的谐波信号进行提取，验证了同步挤压小波变换具有较强的鲁棒性。然而，同步挤压小波变换并不能有效分离瞬时频率相近的分量信号，且重构的分量信号与理论值相差较远[17-18]。

基于此，本文将变分模态分解方法引入土木工程领域，并结合同步挤压小波变换理论，提出一种识别时变结构瞬时频率的新方法。首先，对多分量信号进行连续小波变换得到相应的小波量图，然后根据图中的时频分布情况准确判断分量信号的个数，从而大大提高了计算效率。其次，利用VMD对多分量信号进行分解，弥补了SWT重构单分量信号精度不足的问题。最后，采用同步挤压小波变换识别分量信号的瞬时频率，从而提高了其频率精度。通过一个多分量信号数值算例、一个时变悬臂梁试验以及一个时变拉索试验对所提出的方法进行验证，并与基于希尔伯特-黄变换(Hilbert-Huang Transform，HHT)[19]和连续小波变换(Continuous Wavelet Transform，CWT)[20]的瞬时频率识别结果进行对比，从而验证了该方法的有效性与准确性。

1 基本理论

1.1 变分模态分解

VMD作为一种新型自适应模态分解方法，其主要目的是将输入信号分解为一系列具有稀疏特性的分量信号uk(t)。一般地，多分量信号x(t)可通过式(1)来表示。

x(t)=u1(t)+u2(t)+…+uk(t)

(1)

式中：分量信号uk(t)为具有中心频率和一定带宽的调幅调频信号。

VMD分解方法主要是通过求解模态分量的变分问题来确定各分量信号的带宽和中心频率。在构造变分问题时，其基本原理是对响应信号使用希尔伯特变换、频率混合等信号处理手段，在各阶模态分量之和等于原信号的约束前提下，将有关模态分量的变分问题转化为寻求估计带宽之和最小的模态函数。其具体步骤如下：

首先对分量信号uk(t)进行希尔伯特变换得到对应的单边频谱；其次将得到的单边频谱与e(-iωk t)相乘，从而使每个分量信号的频谱调整至以预估中心频率ωk为中心的频带；最后计算频率混合后信号梯度范数的平方并估计移频后分量信号的带宽，得到如式(2)所示的约束优化问题。

(2)

为求解式(2)中的约束优化问题，引入二次罚函数因子α以保证噪声干扰下的信号重构精度；同时，引入拉格朗日乘法算子λ以保证约束条件的严格性。最后采用拓展拉格朗日表达式L表示如式(3)所示的无约束优化问题：

L({uk},{ωk},λ)=

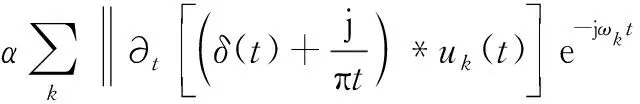
(3)

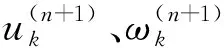
(1) 初始化{u1k}，{ω1k}，λ1，n，并赋初始值为零。

(4)

式中：α建议取值为2 000。

(5)

(4) 根据式(6)迭代更新λn+1。

(6)

(5) 循环(2)～(5)步直至满足式(7)所示的迭代收敛条件

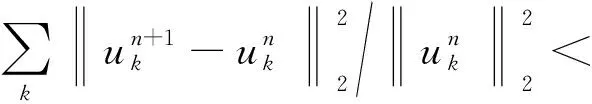
(7)

1.2 同步挤压小波变换

对于给定的母小波函数ψ(t)，对分量信号uk(t)进行如式(8)所示的连续小波变换，其小波变换系数Wu(a,b)为

(8)

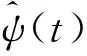
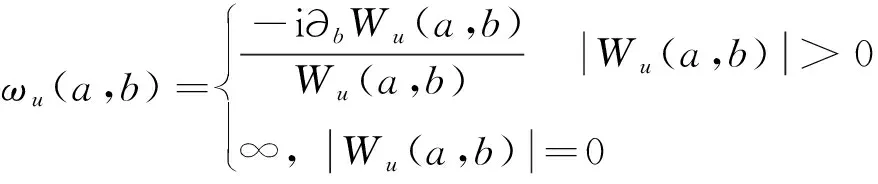
(9)

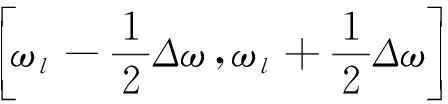
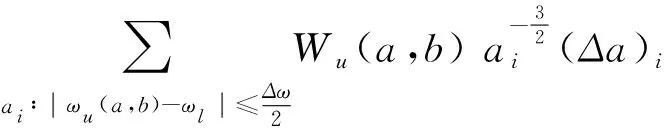
(10)

1.3 基于变分模态分解和同步挤压小波变换识别时变结构瞬时频率

首先，基于变分模态分解和同步挤压小波变换识别时变结构瞬时频率的方法根据小波量图中的时频曲线分布情况确定模态分量个数。其次，通过VMD将响应信号分解成一系列单分量信号，在避免模态叠混现象的同时，也有利于后续的SWT算法。最后，采用SWT识别单分量信号的瞬时频率。该算法的具体流程，如图1所示。

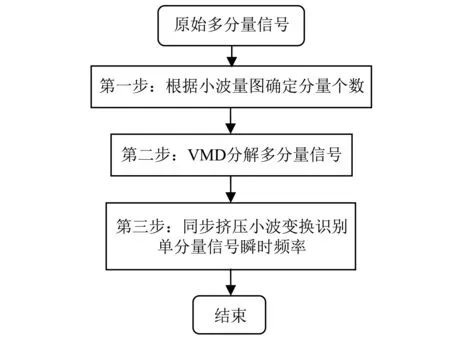
图1 基于变分模态分解和同步挤压小波变换识别时变结构瞬时频率流程图Fig.1 The flow chart of the instantaneousfrequency identification of time-varying structures based on VMD and SWT

2 数值算例验证

考虑如下多分量信号x(t)：

x(t)=x1(t)+x2(t)=cos[2πt+sin(0.5πt)]+
[2+cos(2πt)]cos[4πt+ sin(πt)]

(11)

式中：信号采样频率为100 Hz，采样时间为10 s。分量信号对应的瞬时频率理论值分别为f1=1+0.25cos(0.5πt) Hz和f2=2+0.5cos(πt) Hz。为考虑实际噪声影响，对信号添加20%水平的高斯白噪声，噪声强度由信噪比定义。

(12)

添加20%噪声水平后的信号如图2所示。首先，对含噪信号进行连续小波变换得到如图3所示的小波量图。由图3可知，分量信号的瞬时频率主要集中在[0.5 Hz，1.5 Hz]和[1.5 Hz，4 Hz]两个频率区间内，因此可判断分量信号个数为2。其次对信号x(t)进行VMD分解，得到的分量信号如图4所示。为证明VMD的有效性，采用EMD对原信号x(t)进行分解直至残差函数中的零点个数与极值点个数的差大于1，提取的前2阶本征分量如图4所示。由图4可知，由于噪声的影响，EMD分解出的分量信号与理论值有较大偏差，且端点效应明显大于VMD分解方法。而VMD分解得到的分量信号与理论值更加吻合，且没有出现明显的端点效应。最后，对VMD分解后的分量信号进行SWT并识别分量信号的瞬时频率，如图5所示。图5中同时给出了HHT和CWT两种方法的瞬时频率识别结果。

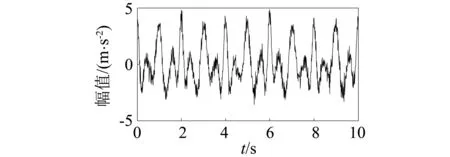
图2 添加20%水平噪声的多分量信号Fig.2 The simulated multi-component signal with 20% Gaussian white noise

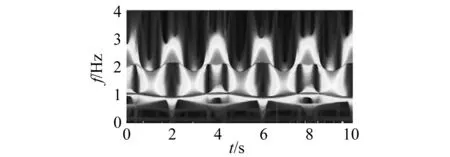
图3 多分量信号的小波量图Fig.3 The wavelet scalogram of the simulated multi-component signal

(a) x1

(b) x2图4 提取的单分量信号Fig.4 The extracted mono-components

(a) x1

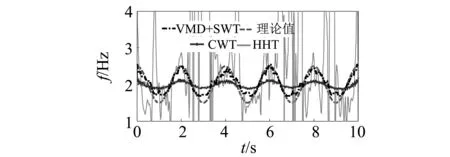
(b) x2图5 瞬时频率识别结果Fig.5 The instantaneous frequency extracted by the proposed method and HHT

从图5可以看出，基于变分模态分解和同步挤压小波变换方法(VMD+SWT)识别的瞬时频率值与理论值更加吻合，且识别效果明显优于HHT和CWT。

为量化瞬时频率的识别精度，采用瞬时频率在整个时间历程内的均方根值作为精度指标(Index of Accuracy, IA)：

(13)

式中：fd(t)为瞬时频率识别值；fe(t)为瞬时频率理论值。精度指标IA值越小，说明识别值与理论值越接近，即精度越高。

表1给出了VMD+SWT、HHT和CWT三种方法所对应的IA值。其中，IA1和IA2分别表示分量信号x1与x2的瞬时频率识别精度指标。由表1可知，针对多分量信号x(t)，VMD+SWT的瞬时频率识别效果明显优于HHT和CWT两种方法。

表1 添加20%高斯白噪声多分量信号的瞬时频率识别精度指标Tab.1 IA of instantaneous frequency identification of the multi-componentsignal with 20% Gaussian white noise %

3 试验验证

为验证变分模态分解和同步挤压小波变换联合方法识别时变结构瞬时频率的有效性和准确性，设计一个质量突变悬臂梁试验与一个刚度时变拉索试验对其进行验证。

3.1 质量突变悬臂梁试验

试验中，铝合金悬臂梁的截面尺寸为40 mm×15 mm，长度为500 mm，重量为0.81 kg，悬臂端的质量块重1 kg。质量块正上方为一块方形磁铁。整个试验装置如图6所示。试验前，测得带重块与不带重块时的悬臂梁的基频分别为21.24 Hz和47.06 Hz。试验过程中，先用力锤在悬臂梁末端施加激振力，并在2 s时利用磁铁吸引质量块使之与悬臂梁分离，从而让悬臂梁的质量产生变化。在质量块与悬臂梁分离后，在2.3 s时再次对悬臂梁进行力锤激励。通过放置在悬臂梁跨中处的加速度传感器(灵敏度：98.7 mV/m/s2)记录悬臂梁在整个时间历程的响应信号，结果如图7所示。

在VMD分解前，对响应信号进行连续小波变换得到如图8所示的小波量图。由图8(a)可知，响应信号的瞬时频率主要集中在[20 Hz，50 Hz]和[250 Hz,280 Hz]频率区间内,从而判断分量信号的个数为2。而图8(b)又表明了[20 Hz，50 Hz]频率区间内的瞬时频率在2s附近发生突变，这与实际试验情况相吻合。对原始响应信号进行VMD分解，得到的一阶分量信号如图9所示。最后，对分解后的分量信号进行同步挤压小波变换以识别悬臂梁结构的瞬时频率，结果如图10所示。与HHT和CWT识别的瞬时频率结果相比，采用VMD+SWT得到的瞬时频率更接近理论值，且没有明显的端点效应。表2中给出了三种方法对应的瞬时频率识别精度指标IA。从表2可以看出，HHT和CWT的识别精度与VMD+SWT相比分别相差了9.1%和18.1%，这也再次证明了VMD+SWT方法的有效性与准确性。

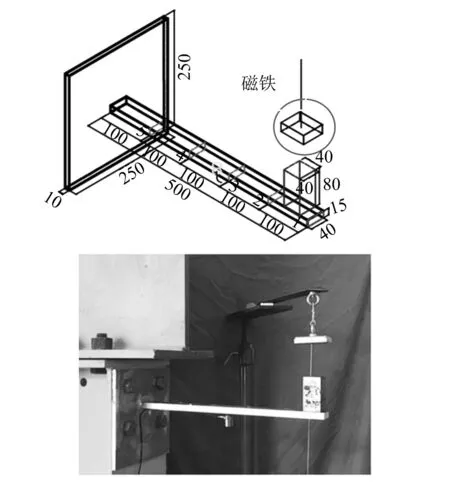
图6 铝合金悬臂梁试验装置图(mm)Fig.6 The aluminum cantilever beam test rig(mm)

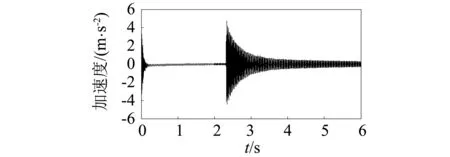
图7 实测响应信号Fig.7 The measured acceleration responses

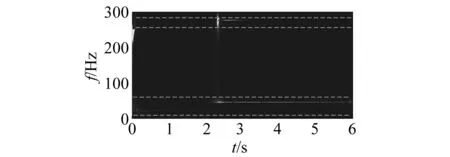
(a) [20 Hz,50 Hz]和[250 Hz,280 Hz]频率区间

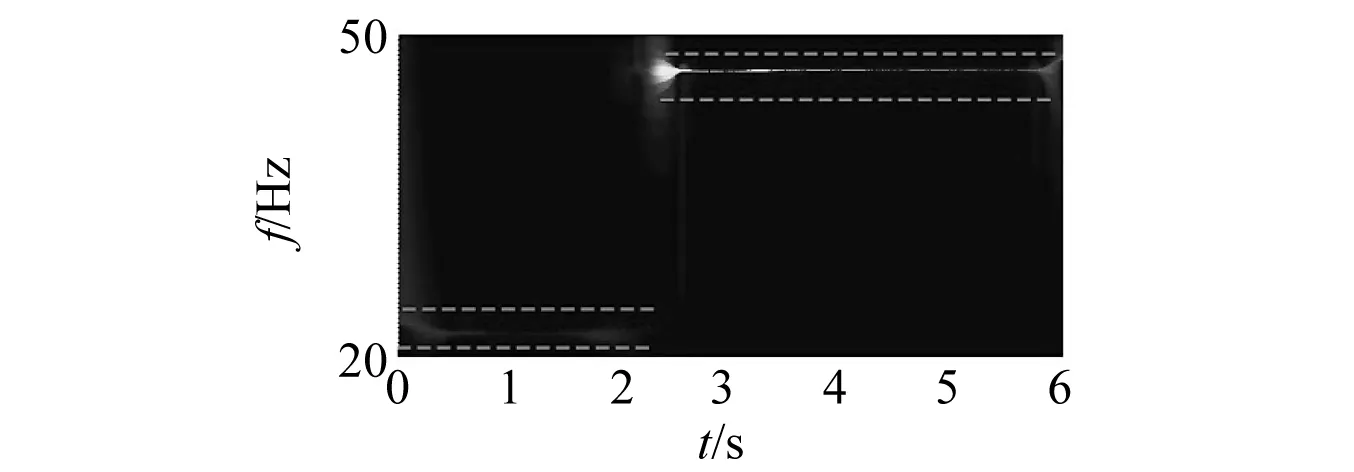
(b) [20Hz,50Hz]频率区间图8 小波量图Fig.8 The Wavelet scalogram

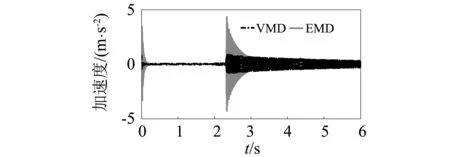
图9 VMD和EMD分解后的分量信号Fig.9 The mono-component signal decomposed by VMD and EMD

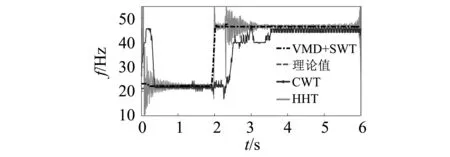
图10 质量突变悬臂梁瞬时频率识别值Fig.10 The identified instantaneous frequency of the cantilever beam with abrupt mass reduction

表2 质量突变悬臂梁瞬时频率识别精度指标Tab.2 The IA of instantaneous frequency identification of the cantilever beam with abrupt mass reduction %

3.2 刚度时变拉索试验

试验所用拉索为一根7φs5的钢绞线，一端用反力架锚固，另一端固定于电液伺服加载系统(MTS)加载系统。两锚固点间的索长为4.55 m，将加速度传感器竖向安装在拉索中部。在使用MTS的作动器对索施加20 kN的预拉力后，通过调整作动器使索的拉力产生变化，从而模拟索的刚度随时间变化的情况。改变索力的同时，用力锤敲击拉索，采集索的竖向加速度冲击响应，采样频率为600 Hz，采样时间为6 s。试验装置如图11所示。

试验过程中模拟了索拉力线性变化和正弦变化两个工况。本文采用“冻结法[21]”，即假定在很小的时间间隔内结构参数保持不变，通过求解系统振动方程的特征值和特征向量近似得到拉索瞬时频率的理论值。

首先，进行拉力线性变化时索的瞬时频率识别，试验时拉力从20 kN开始以1.67 kN/s的速率线性增加。测得索的加速度响应如图12所示。同理，先对响应信号进行连续小波变换得到信号的小波量图，如图13所示。从图13中可以看出，整个时频面上共有两个明显的分量信号。因此，确定VMD中需要选取的模态分量个数为2。利用VMD得到如图14所示的一阶分量信号，然后对其进行同步挤压小波变换，得到的瞬时频率识别结果如图15所示。在图15和表3中同时给出了采用VMD+SWT、HHT和CWT三种方法提取的瞬时频率曲线以及对应的精度指标IA。由此可知：VMD+SWT方法具有较高的精度，且识别效果优于HHT方法和CWT。值得注意的是，虽然CWT提取的瞬时频率识别精度较高，其识别的瞬时频率曲线实际上存在大量毛刺。

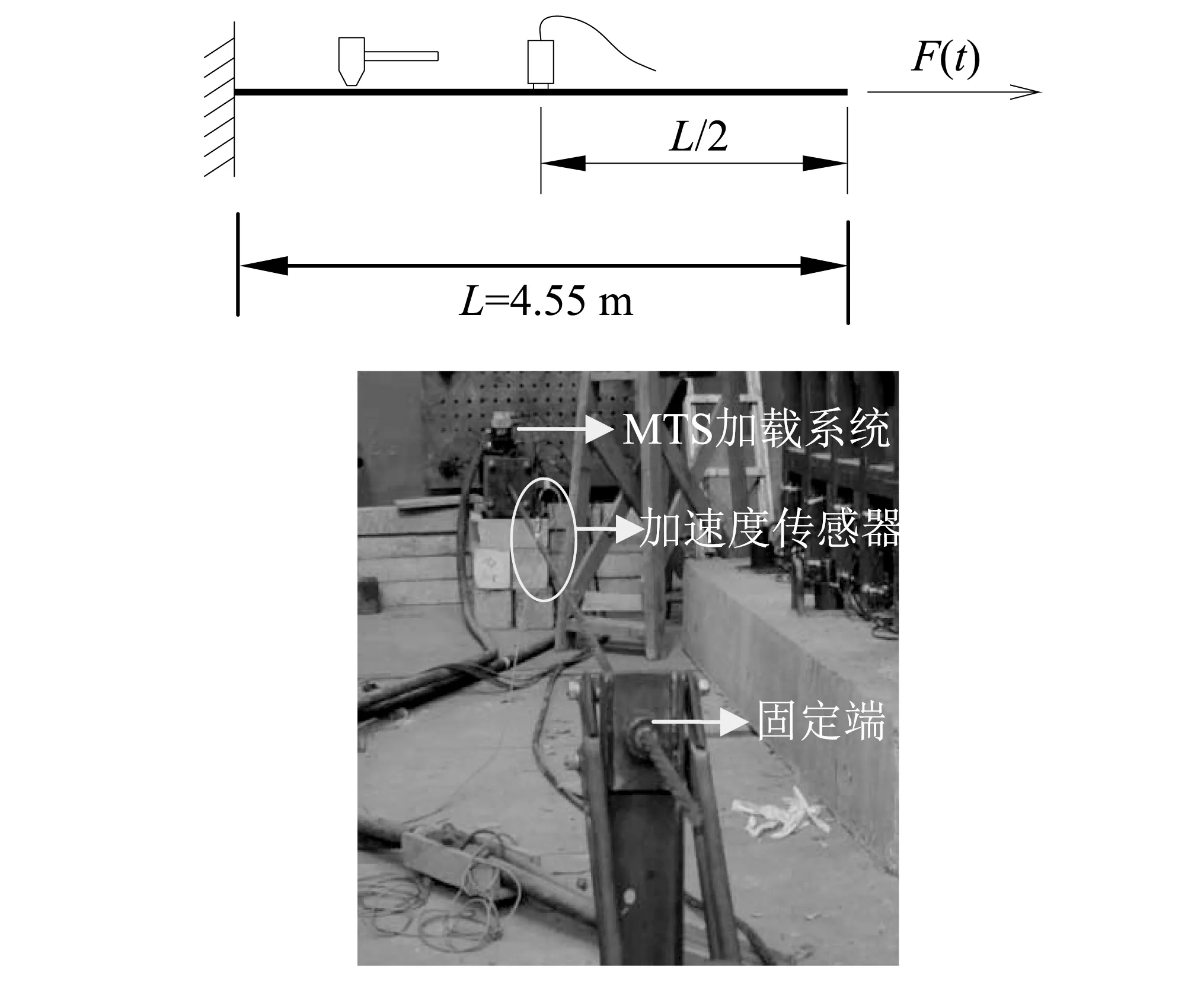
图11 试验装置图Fig.11 The cable testsetup

图12 拉力线性变化时索的加速度响应Fig.12 The measured cable acceleration responses with linearly varying cable tension force

图13 拉力线性变化时实测信号小波量图Fig.13 The wavelet scalogram of the measured cable acceleration responses with linearly varying cable tension force

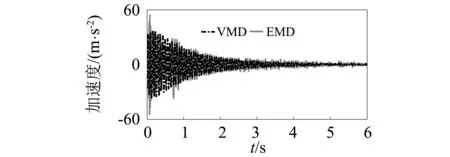
图14 分解后的加速度信号一阶模态分量Fig.14 The first order modal component of the measured cable acceleration responses with linearly varying tension force

图15 拉力线性变化时索瞬时频率识别结果Fig.15 The identified instantaneous frequency of the cable with linearly varying cable tension force

表3 拉力线性变化时索瞬时频率识别精度指标Tab.3 IA of instantaneous frequency identification of the cable with linearly varying cable tension force %

其次，进行拉力正弦变化时拉索的瞬时频率识别。试验时索的拉力成正弦变化，幅度为±10 kN。采集到的加速度响应曲线如图16所示。在采用连续小波变换得到图17所示的小波量图后，确定分量信号分布在[10 Hz，20 Hz]和[40 Hz,50 Hz]两个频率区间范围内，且数目为2。值得注意的是，图17在[20 Hz，40 Hz]之间虽然有能量出现，但其并不连续且明显小于[40 Hz,50 Hz]频带之间的能量，因此可判断为噪声干扰，在确定模态个数k时可忽略不计。然后对信号进行VMD分解，得到如图18所示的一阶分量。最后，对分解后的一阶分量信号进行同步挤压小波变换，得到的瞬时频率识别结果如图19所示。由图19可知，VMD+SWT识别的瞬时频率值虽然与理论值有一定的偏差，但其变换趋势与理论值基本一致，且识别效果明显好于HHT。虽然CWT也能够识别出相应的趋势，但其识别的瞬时频率曲线仍含有较多的毛刺。表4给出的瞬时频率识别方法的精度指标IA则再一次证明了VMD+SWT的准确性。

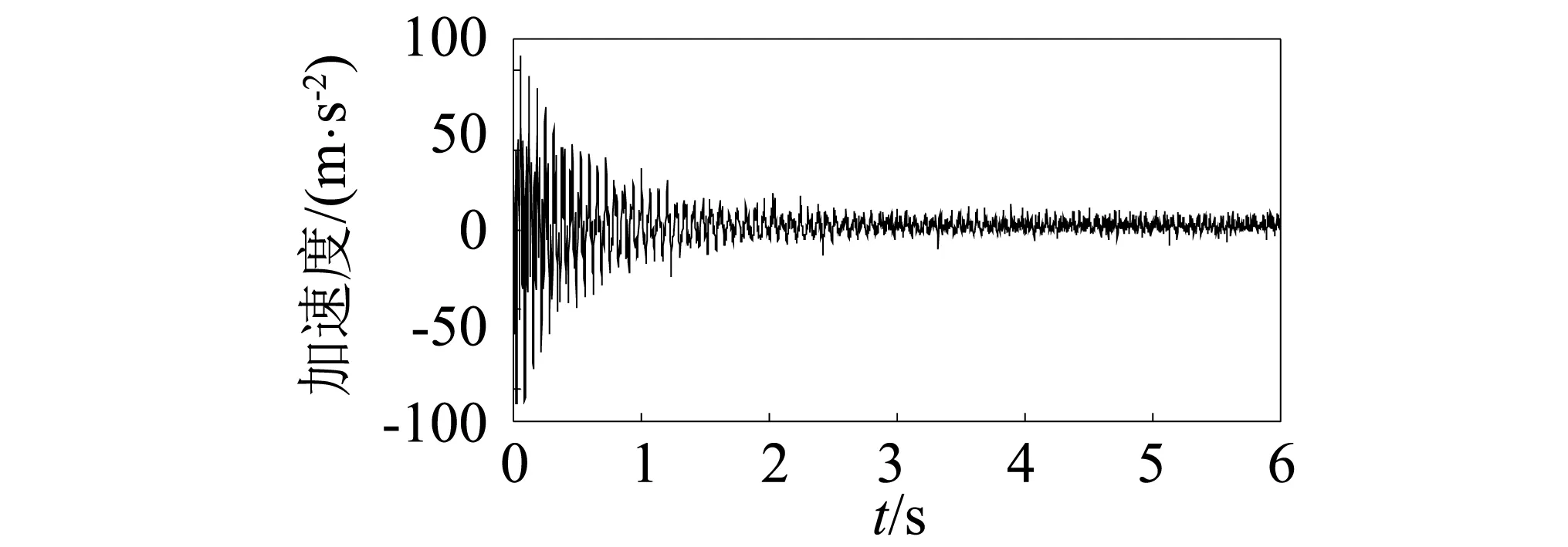
图16 拉力正弦变化时索的加速度响应Fig.16 The measured cable acceleration responses with sinusoidally varying tension force

图17 拉力正弦变化时实测信号小波量图Fig.17 The wavelet scalogram of the measured cable acceleration responses with sinusoidally varying tension force

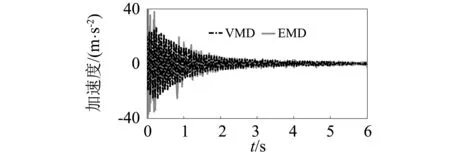
图18 分解后的加速度信号一阶模态分量Fig.18 The first order modal component of the measured cable acceleration responses with sinusoidally varying tension force

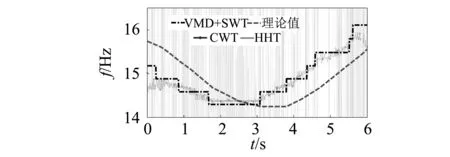
图19 拉力正弦变化时索瞬时频率识别结果Fig.19 The identified instantaneous frequency of the cable with sinusoidally varying cable tension force

表4 拉力正弦变化时索瞬时频率识别精度指标Tab.4IA of instantaneous frequency identification of the cable with sinusoidally varying cable tension force%

4 结 论

自然环境激励下的土木工程结构/构件本质上属于时变和非线性系统，其响应信号呈现非平稳性。因此，本文基于变分模态分解和同步挤压小波变换算法提出一种识别时变结构响应信号瞬时频率的新方法。该方法不仅通过引入小波量图快速便捷地确定响应信号中的模态分量个数，解决了VMD这种非递归模式的频率分割算法的典型问题，同时该方法引入的VMD算法解决了同步挤压小波变换无法准确分解响应信号的问题，从而进一步提高了同步挤压小波变换识别瞬时频率的精度。通过一个数值算例和两个时变结构试验对提出的新方法进行了验证，研究结果表明：

(1)使用VMD时所需的模态分量个数可通过直接观察小波量图中频率分量的个数直接判断。但当小波量图上某一频带范围内的能量不连续且不明显时，该分量可忽略不计。

(2)VMD算法能够有效分离时变多分量响应信号，一定程度上避免了EMD算法中的端点效应和模态叠混等问题。

(3)基于变分模态分解和同步挤压小波变换的联合算法能够有效识别时变结构/构件非平稳响应信号的瞬时频率，且识别精度优于HHT和CWT。