基于FPGA的TDC设计及非线性校正
金博存,杨瑞强
(兰州空间技术物理研究所 真空技术与物理重点实验室,兰州 730000)
0 引言
时间作为七个基本物理常量之一,是目前可实现超高精度测量的物理量之一[1]。在现代科学研究中许多物理量需要转换成时间间隔信息进行测量,时间数字转换器(Time to Digital Converter,TDC)是实现高精度时间间隔测量的技术手段之一。目前,TDC技术被广泛应用于粒子物理探测、深空通讯、频率测量等领域。在飞行时间质谱仪和火星能量粒子分析仪中,可利用TDC对粒子的飞行时间和电流脉冲波形上升时间进行测量,从而完成对粒子种类鉴别。TDC分辨率和精度的高低将直接决定飞行时间质谱仪和火星能量粒子分析仪中的粒子鉴别能力。目前TDC的实现方式大多采取ASIC(专用集成电路)和FPGA实现,相对ASIC-TDC以FPGA实现的TDC具有成本低、高灵活性、研发周期短等优点。基于FPGA内进位链资源实现的TDC因其可实现较高的测量分辨率已成为目前FPGA-TDC领域中研究热点。
1 基于FPGA的TDC测量技术
目前在FPGA实现TDC主要采取Nutt内插法[2],将待测时间间隔分为粗、细两个过程。测量原理如图1所示,粗测量单元完成对时钟周期整数倍的时间间隔的测量,而细测量单元则完成对开始(Start)结束(Stop)不足一个时钟周期的时间间隔的测量,待测时间间隔ΔT可由式(1)得到。

式中:T0为计数器的时钟周期;NC为计数器的测量值;Ta和Tb为不足一个时钟周期的时间间隔。
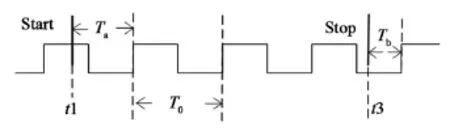
图1 粗计数结合细测量原理图Fig.1 The measurement of coarse counter combined with fine time
粗测量一般采用计数器来实现,计数器可以使TDC获得更大的测量动态范围,再结合其他细测量的技术对不足一个时钟周期的时间间隔进行测量。从技术途径,在FPGA中实现细测量内插方式可以分为两类:一是如何获取已知延迟时间更小的延迟单元(如延迟链法,脉冲收缩法);二是如何将待测时间间隔进行等比例的放大(如游标法)[3-5]。本设计的FPGA-TDC采用延迟链法构建细测量单元,延迟链法原理如图2所示。信号在延迟链上传递由于每个延迟单元延迟时间已知,可利用通过触发器来锁存延迟链的状态从而获得待测时间间隔。

图2 延迟链法原理图Fig.2 Diagram of the delay line
通过研究发现FPGA中的进位链具有延迟时间小且延迟时间相对稳定的特点[3],因此设计通过FPGA内部的进位资源构建延迟链来实现TDC的细测量单元。
2 FPGA-TDC的实现
设计选用Xilinx的Spartan 6系列的XC6SLX16 FPGA来实现TDC电路。图3为所设计TDC电路整体结构框图,整个TDC测量系统可以划分为四个部分:“粗”测量单元、“细”测量单元、编码单元、数据缓存单元。
在Spartan6系列的XC6SLX16器件中,最多能实现236级加法进位链。在仿真时,设计196级加法器级联其延迟时间约为4.1 ns。由此可以算出TDC测量系统中计数器的时钟频率应为f=1/T=1/4 ns=250 MHz。为了避免计数器的亚稳态现象,粗测量单元采用两个工作在正反250 MHz时钟下的12位计数器,可实现的TDC电路的测量范围为:16.384 us。

图3 TDC整体结构框图Fig.3 Block diagram of the time-to-digital converter
细测量单元采用Spartan6器件中进位链资源来构成加法延迟链进行时间内插。在Xilinx的Spartan6上使用加法器生成进位链时,首先通过Xilinx FPGA开发软件ISE中的Spartan6器件原语去调用Slice中的进位链资源,然后通过约束语句描述进位链的位置信息。将所有进位链中的加法器的被加数端置1,初始时刻所有进位链上的加法器输出端为1。当起始信号到来时位于进位链中的加法输出依次从1跳变为0,此时通过D触发器锁存进位链的状态即可获得待测时间间隔。进位链中的D触发器采用Slice中自带的D触发器,确保每一个延迟单元的输出信号能够被完全一致的采集。
在对进位链构成的细测量单元进行布线后,仿真时发现每一级加法器的输出信号的延迟时间并不相等。通过查看Spartan6的用户手册,发现Spartan6器件Slice中的进位链是一种超前进位链,这种超前进位的结构是造成每一级加法器输出延迟时间不一致的原因。为了获得延迟时间稳定的最小延迟单元,对进位链中的延迟单元进行了重新的划分。将一个Slice内部的四个加法器作为一个最小延迟单元其延迟时间约为83 ps。整个细测量单元共使用196级加法器构成50个最小延迟单元,总延迟时间约为4.1 ns。由延迟链法原理可知,细测量单元输出数据为n位温度计码的格式,不利于后期的存储和处理。因此,设计编码单元将细测量的输出转换成普通的二进制码。
最后,利用FPGA内部的RAM资源作为数据缓存单元,对粗测量和细测量结果进行保存。此外该RAM单元还可用于构建相应的查找表完成对细测量单元的非线性校正工作。
3 码密度测试平台
进位链中延迟单元延迟时间的不均匀性是造成TDC测量精度下降的主要原因之一,此外通过FPGA设计软件仿真的延迟时间并不能反映其真实测量的延迟情况。因此,应设计相应的测试平台对TDC延迟单元的延迟时间进行测试。采用码密度测试法对TDC进行测试,码密度测试法是基于大量数据统计的测试方法[67]。对于随机的测试信号当统计次数足够多时,不同码值被击中的频率即可表征相应码值的时间宽度。测试时,向延时链中输入大量的随机跳变脉冲,假设有N个随机跳变脉冲,第i个延迟单元采样得到的码密度数据为M,可以得出第i个延迟单元的延迟时间M为:

式中:Ti为第i个延迟单元的延迟时间;N为码密度测试总数;M为第i个延迟单元的统计次数;TCLK为系统的时钟周期(4 ns)。码密度测试法的随机信号在实际应用中很难产生,因此在测试时使信号源产生一个与时钟频率不相关的周期信号来代替随机信号。信号源采用AFG3102输出一个4 MHz的信号模拟大量随机脉冲的产生源,将AFG3102输出信号通过同轴电缆连接至FPGA延迟链的输入端口,延迟链中触发器采样频率为250 MHz由FPGA内锁相环提供。在FPGA例化一个RAM来存储每次细测量的结果,最后将RAM中的数据通过串口发送至PC端进行后续的处理。测试样本总数为200 000个,测试所得的码密度直方图、微分非线性、积分非线性如图4~图6所示。

图4 码密度直方图Fig.4 Histogram of code density

图5 微分非线性图Fig.5 Diagram of differential nonlinearity
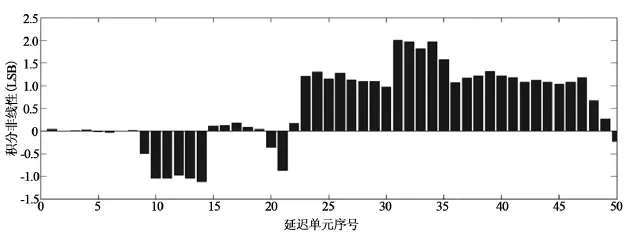
图6 积分非线性图Fig.6 Diagram of integral nonlinearity
从测试结果可以看出延迟链中存在延迟时间过长的延迟单元,这些过长的延迟单元造成TDC测量的非线性程度增加。如果延迟单元的微分非线性大于1 LSB,会产生失码现象从而导致TDC的时间测量分辨率性能降低。为找到造成这些延迟单元延迟时间过长的原因,通过查看FPGA底层布局布线,发现产生这一现象的原因是进位链的长度超出了Spartan6器件内部一个Clock Region所能覆盖的最大长度,使得进位链布线过长增加延迟单元延迟时间。进位链的结构在FPGA中是固定的,通过手动布线改变这些进位链的布线资源并不合理且容易引入额外的延迟时间。因此采用软件算法上校正的方式对其进行修改以提高TDC的测量性能。
4 非线性校正
4.1 校正方式
由前仿真和码密度测试法得知,其延迟链中存在较大延迟时间的延迟单元,这些延迟单元的存在会影响TDC时间测量的精度。因此,需要对延迟链进行校准以提高测量的准确度。对延迟链的校正方法有两种:一种是平均法(average delay);另一种是bin-by-bin的方法,bin-by-bin校正即通过码密度测试得到每个延迟单元的延迟时间然后制成相应的查找表对其进行校准[8]。平均法其原理是产生一个时间间隔已知的信号,让这个延迟时间已知的信号通过延迟链,从输出结果可以得出在延迟链上传播多少个延迟单元。假设两次记录的位置为N1和N2,则每个延迟单元的平均延迟时间td为:

式中:td为延迟单元的平均延迟时间;ts为总延迟时间;N2和N1为信号在延迟链中传播所记录延迟单元的位置。平均法并不能对每个延迟单元延迟时间进行校准,尤其是对于延迟时间较大延迟单元,平均法会产生较大的误差。而采用bin-by-bin校正方式可以对延迟链上的各个延迟单元进行校准。因此,设计采用bin-by-bin的校正方式,利用码密度测试得到的延迟链的各个延迟单元的延迟时间,将各个单元的延迟时间大小存为一个数组wk置于RAM中作为每次测量之后的校正向量,输入信号传播到第n个延迟单元的延迟时间可表示为:

式中:tn为信号传播到第n个延迟单元的延迟时间;wn为第n个延迟单元的延迟时间。在编码单元获取细测量结果后可根据式(4)在RAM中制作相应的查找表,进而获得待测时间间隔。采用bin-by-bin的校正方式可以对每一个延迟单元的延迟时间进行校准,尤其是针那些对延迟时间较大的延迟单元bin-by-bin的校正方式可以提高TDC的测量准确性。
4.2 TDC精度测试
在完成对TDC延迟链的校正之后需设计相应测试平台验证TDC整体测量的准确度。利用长度不同的同轴电缆(RG174)来产生固定时间间隔,并利用TDC测试固定的时间间隔以验证TDC的测量精度。在测试前首先应对同轴电缆延迟时间进行测量,利用信号源AFG3102和示波器MDO4104B测试不同长度的同轴电缆延迟时间,其延迟时间如表1所列。

表1 同轴电缆长度延迟时间Table1 The delay time of coaxial-cable
根据最小二乘法对测量到的同轴电缆的长度和延迟时间进行拟合,得到拟合线性方程为:

式中:x为同轴电缆长度;Y同轴电缆的延迟时间。拟合相关系数为R-square=0.999 3,剩余标准差(RMSE)为:0.07拟合效果良好。由此可知单位cm同轴电缆(RG174)延迟时间约为51 ps左右。利用不同长度的同轴电缆构造不同的延迟时间,并利用TDC测量已知的时间间隔以检验经过bin-bybin校正后的TDC测试精度。利用TDC多次测量固定5.10 ns(长度差在1 m的RG174同轴电缆)的时间间隔测量结果如图7所示,测量平均值为5.21 ns,标准差为0.140 ns。利用TDC多次测量固定7.60 ns(长度差在1.5 m的RG174同轴电缆)的时间间隔测量结果如图8所示,测量平均值为7.52 ns,标准差为0.168 ns。

图7 5.1 ns时间间隔精度测试结果图Fig.7 Performance of the 5.1 ns time interval accuracy
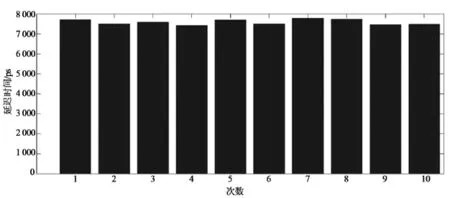
图8 7.60 ns时间间隔精度测试结果图Fig. 8 Performance of the 7.60 ns time interval accuracy
由此结果可以看出采用bin-by-bin的校正方式可将TDC的测量精度的最大偏差校准到约等于一个最大延迟单元的延迟时间。
5 结论
完成了基于Spartan6-FPGA的TDC电路设计与实现,针对设计中遇到的问题,做出了一系列解决方案。采用码密度测试法对延迟单元的延迟时间进行测量,针对TDC延迟链中存在延迟时间较大的延迟单元,采用bin-by-bin的校正方式对TDC的细测量结果进行校正以提高TDC的测量精度。设计的TDC电路可实现测量指标为:TDC最小分辨(LSB)83 ps、TDC测量精度小于2 LSB、TDC测量动态范围16 us。

