考虑伺服系统增益不确定的船舶动力定位自适应有限时间控制
张国庆 黄晨峰 吴晓雪 张显库
由于海洋资源开发和海洋工程作业的需要,人们对于深海作业的浮式生产系统(半潜平台、生产油船、供给船等)的定位方式日益重视.船舶动力定位技术是指在不借助锚泊系统的情况下,船舶利用自身的推进装置抵御风、浪、流等外界扰动的影响,以一定的姿态保持在海面某一目标位置或精确地跟踪某一轨迹,以完成各种作业的功能[1−3].它具有不受海水深度影响、定位准确快速等优点.由于水面船舶不可避免地将遭受如风、浪和流等外部环境带来的强扰动,以及复杂的水动力的不确定性,给控制器的设计带来巨大的困难[4−6].同时,船舶的纵荡,横荡和艏摇三个自由度之间存在着强耦合,且其中任一自由度的不稳定都将对整个系统造成巨大影响,所以要求三个自由度同时稳定[7].Do[8]基于李雅普诺夫直接法提出了一种输出反馈的控制方法,通过构造自适应观测器来估计船舶的速度和未知参数,设计的控制器能够迫使船舶位置和艏向角渐近稳定于期望值.Du等[9]采用高增益观测器对船舶的位置和艏向角进行估计,并引入径向基函数(Radial basis function,RBF)神经网络补偿船舶模型的不确定性,设计的控制器不需要模型和外界扰动的先验知识.王元慧等[10]基于非线性模型预测控制技术设计了船舶动力定位控制器,并通过仿真验证了非线性模型预测控制器的有效性.Hassani等[11]提出了一种基于多模型的滤波理论的反馈控制方法,通过对时变海洋环境中的高频部分进行滤波,使船舶在恶劣海况下的动力定位性能得到显著提高.Grovlen等[12]通过引进矢量逆推的概念,在控制器设计过程中忽略了时变环境扰动的影响,从而简化了船舶动力定位控制律逆推方法,并且得到全局指数稳定的结果.以上研究大多得到的是渐近稳定或指数稳定的控制结果,鲜有基于有限时间理论[13]的船舶动力定位控制方法的相关文献.为此,在考虑伺服系统增益不确定的前提下,针对模型参数不确定、外部扰动未知的船舶动力定位控制问题,本文提出了一类自适应非奇异终端滑模的控制方法,并通过Lyapunov稳定性理论证明了闭环系统是实际有限时间稳定的,最后采用一艘供给船进行数值仿真实验,证明了所设计控制器的有效性.本文的创新点主要有:1)设计了一种终端滑模的控制方法,实现了船舶动力定位系统运动学回路和动力学回路的双环有限时间稳定,且收敛精度高,鲁棒性强;2)针对伺服系统的增益不确定问题引入自适应参数学习律,避免了再在执行部分构建控制命令–执行变量之间的闭环,得到了控制输入为实际可测螺距变量的结果,更易于工程实现.
1 问题描述与预备知识
1.1 预备知识
为了方便后续分析,这里给出有限时间稳定的相关定义和引理[14−17].考虑如下非线性系统:

其中,x为状态变量,入变量,为连续函数,且f(0)=0.如果系统(1)是Lyapunov稳定的,且存在时间函数,使得对于所有的t≥恒成立,则称系统(1)是有限时间稳定的[14].
引理1.针对式(1)描述的系统,假设存在连续可微的正定函数,标量λ>0,0<α<1和0<ζ<∞,使得式成立,则可以说系统 x˙ =是PFS的[5].且到达时间为
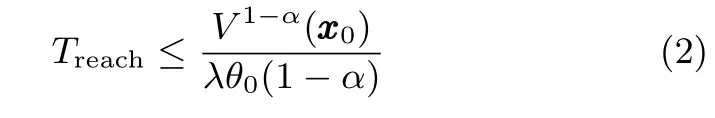
引理2.对于任意实数xi,如果存在r∈(0,1),则有下述不等式成立[16]:
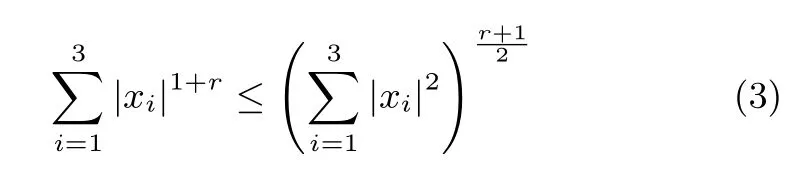
引理3.对于任意实数xi,如果存在r∈(0,1),则有下述不等式成立[17]:
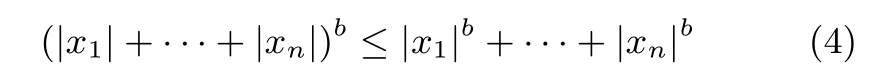
1.2 动力定位船舶的数学模型
假设动力定位船舶是左右对称的,只考虑船舶前进、横漂和艏摇3个自由度的平面运动,则动力定位船舶的非线性模型为



假设1.惯性矩阵为M是正定可逆的对称矩阵,即M.该假设与水面船舶船体左右,前后近似对称的特性是相符的.
假设2.M和 N(v)为未知模型参数矩阵且上界已知,其满足下列条件:

假设3.在式(6)中,τw为上界已知的扰动,即存在向量且.
注1.考虑实际海洋工程中主机提供给推进器的能量是有限的,因此,对于特定的船舶来说,推力系数矩阵必须满足为未知常量且仅用于稳定性分析.
2 非奇异终端滑模控制器设计
将船舶动力定位系统的控制器设计分为两步.首采用Lyapunov直接法设计运动学回路的有限时间虚拟控制律;然后基于非奇异终端滑模的方法设计系统的动力学回路控制器,同时考虑船舶动力定位系统执行器的增益不确定问题,最终设计出符合海洋工程实践,控制输入为调距桨可变螺距的船舶动力定位自适应有限时间控制律.
步骤1.船舶动力定位的期望轨迹为,定义船舶动力定位的位置误差为

对时间求导,可得

将v视为虚拟控制向量,选择镇定函数向量αv为

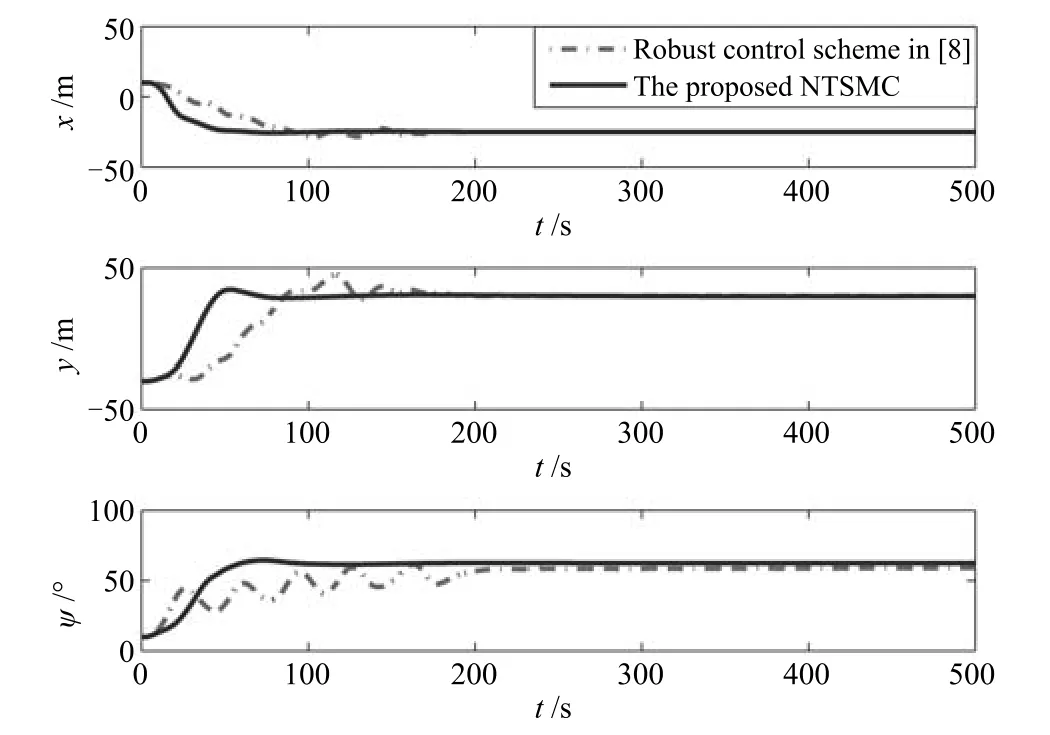
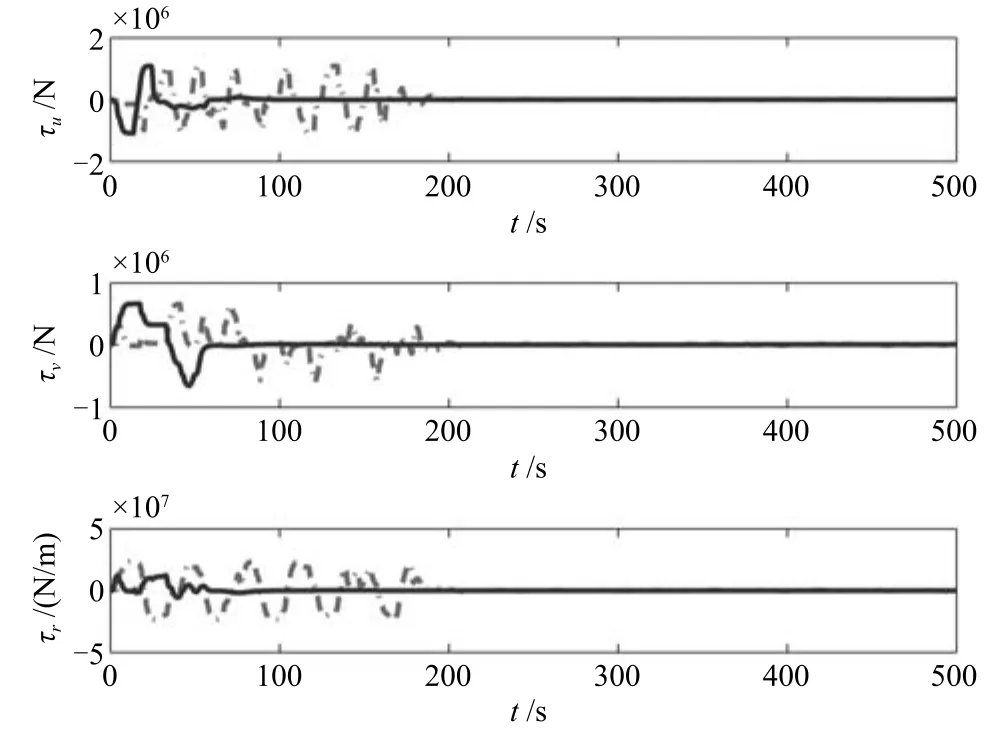
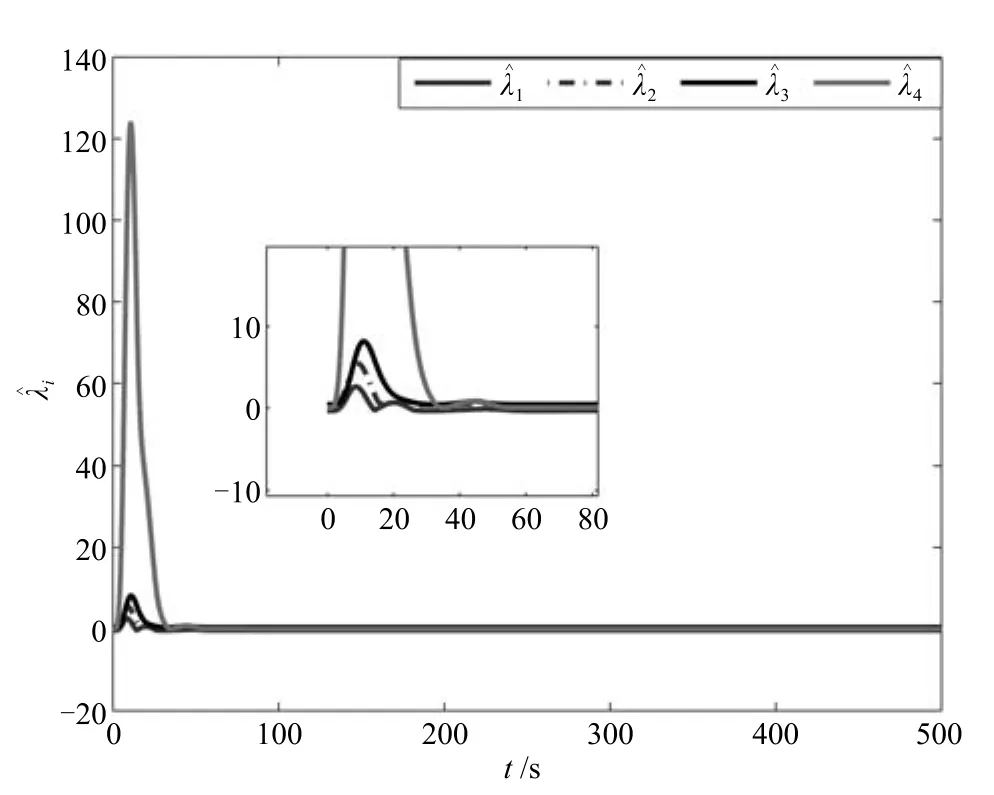
式中,χ为位置误差的正定对称设计矩阵,且0 步骤2.设计如下非奇异终端滑模面: 其中,p为正整数且满足为正定的设计参数矩阵.表示向量的分数次幂 对非奇异终端滑模面(17)求导得 根据式(16)和式(18),得 第三,雷可夫和约翰逊声称体验哲学不继承任何业已发展的哲学理论,是一种全新的哲学理论[3]496,并认为由于它的创建,两千多年来人类关于哲学的思考已成过去,哲学再不是原来的样子[3]3。如此言过其实的话语完全忽略了马克思主义关于思维、认识的观点。目前,国内已有学者将体验哲学与马克思主义哲学观进行了对比研究[9-10],结论是体验哲学观与马克思主义认识论在许多方面有共同之处,这表明体验哲学中的许多论点是马克思主义认识论早已阐释过的。如此看来,体验哲学的观点并不全是创新性的,说它“彻底改变了传统的西方哲学观”[11]是站不住脚的。 根据式(7)得: 其中, 其中,αp是控制律,的伪逆矩阵,是λ的估计值且.则非奇异终端滑模控制律设计为 Φ为待设计与状态有关的函数.设计函数Φ为 其中,ς>0. 注2.上述控制器设计时,由于在滑模面设计时引入了符号函数,必然会引起系统高频振动,因此采用饱和函数代替符号函数消除抖动[18−19].定义饱和函数的形式如下: 其中,4为边界层厚度. 根据文献[20]的方法在线更新的值.相应的自适应律为 定理1.考虑执行器增益不确定问题,针对已知模型参数不确定上界和外部扰动上界的船舶动力定位系统(5),(6),(7),在终端滑模控制律(22)及自适应律(26)的作用下,船舶闭环系统内的状态在有限时间内收敛到且保持在期望值的一个领域内. 证明.构造系统的Lyapunov函数: 将V对t求导得: 将控制律(22)和自适应律(26)代入上式,得 其中, 对于任意标量ξ0>1/2,有下列不等式成立: 由引理2可知,系统是有限时间收敛的,且系统的状态变量会在有限时间收敛到如下稳定域内: 即滑模面的一个邻域内: 注3.在实际海洋环境中,船舶的航行始终会受到风、浪和流的干扰,导致本文控制律下动力定位船舶的闭环系统为实际有限时间稳定,这也与文献[21]相符合.实际上,终端滑模控制器的强鲁棒性和快速收敛性可以通过增大控制器增益的方法来体现,但单一加大控制参数势必会引起控制输入的抖增而导致执行器过载损坏. 为了验证设计的船舶动力定位自适应终端滑模控制器的性能,以一艘动力定位供给船为仿真对象进行仿真研究.该供给船的质量为m=4.591×106kg,长度为L=76.2m,配备有两个主推进器和首尾侧推,推进器布置如图1所示,其中ly1=5m,ly2=−5m,lx3=25m,lx4=−25m.模型参数如下: 本文采用文献[6]中的风、浪、流的机理模型所产生的外界环境干扰力和力矩作用于船舶模型.其中,海浪模型和风模型是耦合的,即风生浪模型.设置海洋环境干扰为6级,具体参数为:风向ψwind=45◦,风速Vwind=12.5m/s,流向βcur=120◦,流速Vcur=0.5m/s. 图2∼4是动力定位船舶在两种控制律(本文有限时间控制律和文献[8]中渐近稳定控制律)下的控制效果对比,从图中可以看出,两种控制器均能保持系统最终稳定状态.图中实线为本文控制律下的控制结果,虚线为文献[8]中控制律下的控制结果. 图2为供给船的平面位置(x,y)及艏向角ψ的变化曲线,仿真试验表明,两种控制律都能迫使供给船的空间位置和艏向角收敛于期望值,且本文所设计控制器在50s左右稳定优于文献[8]中200s左右稳定时间,进一步实验表明供给船在运动到期望的目标位置以后能够保持在该期望位置附近,实现动力定位的控制目标. 图1 供给船推进器布局图Fig.1 Thruster configuration diagram for the supply vessel 图2 船舶的位置和艏向角x,y,ψ历时变化曲线Fig.2 Position and orientation variablesx,y,ψunder different control laws 图3 船舶速度u,v,r历时变化曲线Fig.3 The kinematic variablesu,v,runder different control laws 图4 船舶动力定位控制律历时变化曲线Fig.4 Curves of ship dynamic positioning control laws 图3和图4分别为供给船速度和控制律历时变化曲线,得益于终端滑模控制器强鲁棒性和高稳态精度的特点,可以看出在本文控制律式下,供给船的速度变量得到快速镇定. 图5 增益不确定估计参数1,2,3,4历时变化曲线Fig.5 Curves of estimations for gain uncertainties1,2,3,4 图6 执行器螺距控制输入历时变化曲线Fig.6 Curves of the propeller pitch of actuators 本文针对水面船舶的动力定位问题,考虑船舶在海洋工程实践中存在的伺服系统增益不确定现象,通过对模型参数不确定和海洋环境扰动上界的估计,设计了一种自适应终端滑模控制器.利用终端滑模具有有限时间收敛、鲁棒性强且收敛精度高的优点实现船舶运动学回路和动力学回路的有限时间收敛.同时对执行器的增益系数进行参数自适应,进一步得到了控制输入为调距桨可变螺距输入的结果.借助Lyapunov稳定性理论证明了设计的自适应终端滑模控制器是实际有限时间稳定(PFS)的;最后,以一艘配备两个主推进器和首尾侧推的供给船进行了仿真研究,仿真结果验证了自适应终端滑模控制器的有效性.
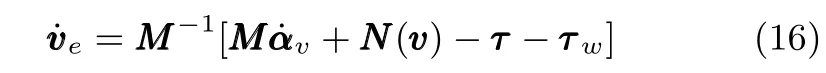


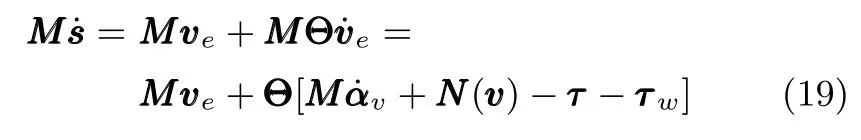
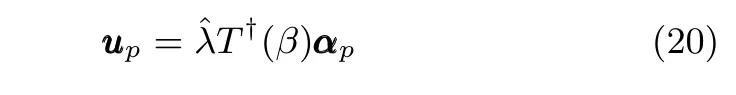
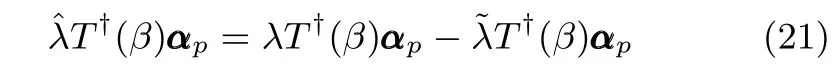

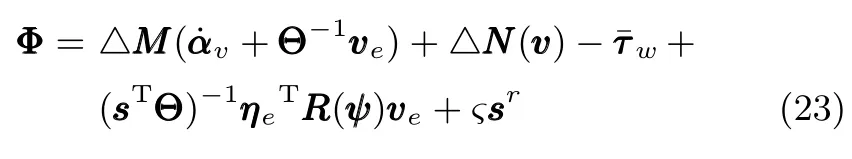



3 系统稳定性分析


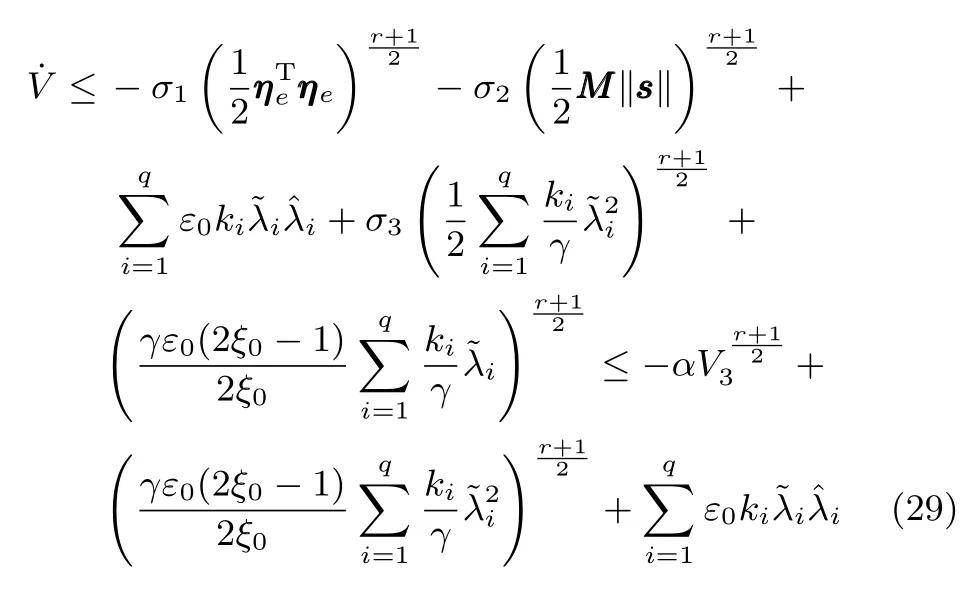

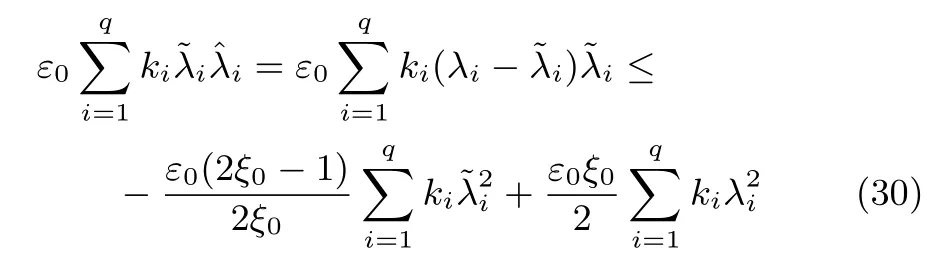


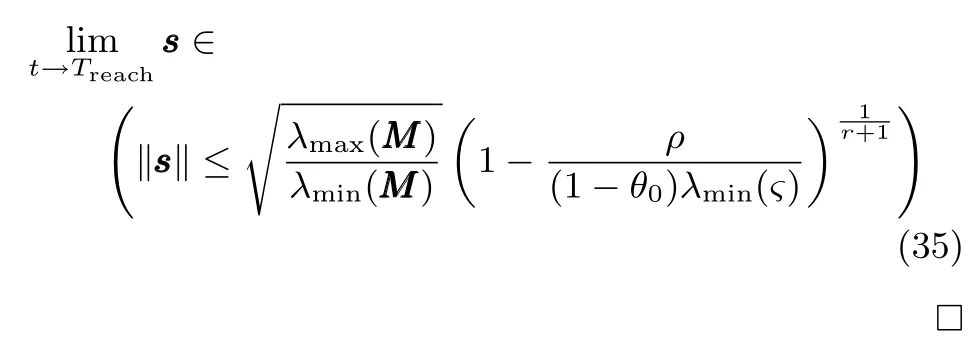
4 仿真研究





5 结论

