一类不确定非线性系统的重复学习控制
李鹤 孙明轩 张静
学习控制能够处理有限时间区间上重复作业的控制系统.这种控制算法通过每次实际运行结果修正控制输入,随着迭代次数的增加不断提高控制性能,因此在实际系统中得到了广泛应用,如工业机器人、数控机床、硬盘驱动装置、化工间歇过程等[1−2].
近年来,基于Lyapunov方法的迭代学习控制引起人们的关注[3−5].设计学习控制器时需要处理系统存在的不确定性,通常包括参数不确定性与非参数不确定性.目前,有许多关于工业机器人系统迭代学习控制的研究成果[6−9];文献[10]针对一类非线性系统,采用自适应算法学习固定常值参数;文献[11]针对工业机械臂,通过一类自适应迭代学习控制算法估计不随迭代轴变化的时变参数;文献[12]将高阶内模与学习控制算法相结合,处理随迭代轴变化的时变参数;文献[13]针对非线性参数不确定系统,基于自适应重复学习控制算法学习周期参数;文献[14]通过鲁棒自适应及Backstepping方法分别处理参数与非参数不确定性;文献[15]采用神经网络及傅里叶级数逼近方法,估计周期已知的时变参数;文献[16]通过自适应迭代学习控制算法,处理一类高阶非线性系统的参数不确定性与初值问题;文献[17]针对具有未知控制方向的纯反馈非线性系统,通过自适应迭代学习控制策略,处理系统存在的参数不确定性;文献[18]通过周期自适应学习控制方法,解决了输入饱和非线性系统中含时滞的参数不确定性.此外,文献[19]通过自适应迭代学习控制方法,处理纯反馈非线性系统中的参数不确定性与非一致期望轨迹.可参数化的不确定系统,通常要求参数为固定常值、周期或时变参数,而实际系统的不确定性不仅仅包括可参数化情形,因此人们开始研究非参数不确定性.文献[20]针对一类连续非线性系统,通过迭代学习控制方法,处理非参数不确定性;文献[21]通过鲁棒自适应迭代学习控制方法,解决了离散非线性系统中的参数与非参数不确定性;文献[22]将迭代学习控制与模糊逼近相结合,利用反步控制策略,以处理纯反馈非线性系统的非参数不确定性;文献[23]针对控制增益与状态有关的多输入多输出非线性系统,通过迭代学习控制算法处理非参数不确定性;文献[24]通过鲁棒迭代学习控制方法,解决了一类连续非线性系统的非参数不确定性.文献[20,23−24]均考虑控制增益与状态有关的控制系统,并且非线性函数满足Lipschitz条件,特别地,所提出的控制方法,需要已知的信息包括:控制输入增益的最小值与非线性函数的界函数,然而实际系统中该界函数很难精确获得.
迭代学习控制算法要求每次迭代开始时保证严格的初始定位,系统初态与参考轨迹的初值一致,然而实际系统的复位精度有限,往往会导致系统存在初始误差,从而影响控制精度.因此,为提高系统的控制性能,解决初始定位问题是有意义的.重复学习控制,要求系统每次迭代的初值与前一次迭代的终值相同,且参考轨迹是封闭的,有效回避了迭代学习控制的初始定位问题.与重复控制不同的是,重复学习控制放宽了对周期的要求.文献[9]提出重复学习控制方法,通过自适应重复学习机制处理机械臂系统的常参数不确定性.文献[25]考虑了迭代学习控制中5种不同的初始条件,其中第5种情况与重复学习控制的初始条件相同.如何通过重复学习控制解决非线性系统的非参数不确定性问题,是学习控制领域中一项重要的研究内容,特别地,对于未知界函数情况下的非参数不确定性,目前几乎未有相关的研究成果.
基于以上讨论,本文针对一类在有限时间区间上执行重复任务的不确定非线性系统,提出一种用于解决满足Lipschitz条件非参数不确定性问题的控制方法.该方法采用带死区修正的学习律,对期望控制输入与界函数平方进行估计,以避免参数的正向累加导致系统发散.通过该学习律设计重复学习控制器,采用带死区的Lyapunov函数,保证了闭环系统所有信号的有界性,并且实现了跟踪误差在有限时间区间上收敛于给定的邻域.此外,所提出的控制方法能够处理与状态有关的非线性控制增益.与文献[20,23−24]不同的是:1)对于满足Lipschitz条件的非参数不确定系统,本文并未假设其界函数已知.文中基于重复学习方法,对该界函数的平方进行估计.在已发表的相关文献中,这一做法尚未见报道;2)本文设计带死区修正的学习律,对该界函数的平方进行估计,这不仅方便了收敛性分析,并且避免了参数的正向叠加对系统收敛性能的影响,同时,利用带死区的Lyapunov函数,以保证系统跟踪误差收敛于给定的邻域;3)本文所设计的重复学习控制算法,以尽可能少的系统模型信息(仅已知控制输入增益最小值gmin)处理非参数不确定性,从而较少地依赖于系统信息,更方便于控制器的实现.进一步,本文通过仿真与实验验证了所提控制方法的有效性.
1 问题描述
考虑一类不确定时变非线性系统
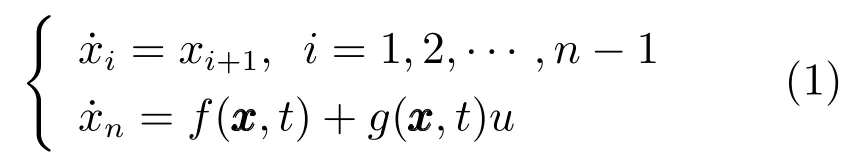
假设1.控制输入增益函数符号已知,且存在常数gmin满足.
注1.假设1中,要求为严格正的或者严格负的.不失一般性,本文假定,,其中gmin为已知常数.
假设 2.非线性函数满足:,其中,定义Lipschitz系数(即时变函数)分别为非线性项的界函数.
注2.假设2中,在有限时间区间上为Lipschitz连续,且本文并未要求界函数lf(t),lg(t)已知.
本文采用重复学习控制算法,受控系统应具有如下属性[9]:
属性1.系统在有限时间区间上重复运行.
属性2.期望状态是给定且封闭的.
属性3.系统每次运行的初值与前一次运行的终值一致.
属性4.被学习的时变参数与迭代轴无关.
属性5.在所有作业区间中系统动态特性相同.
根据属性1~5,系统(1)在有限时间区间[0,T]上重复运行,满足:
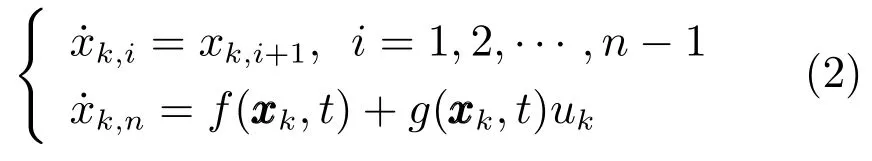
其中,k=0,1,2,···为迭代次数.
本文控制目标为,针对系统(2),设计重复学习控制器uk(t),使得系统状态随着迭代次数k的增加,在有限时间区间[0,T]上收敛于给定的期望状态.

其中,
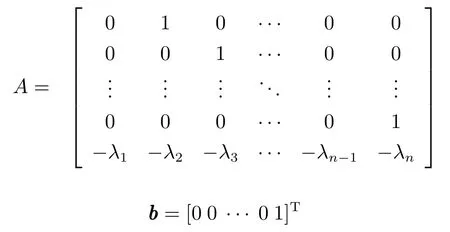
未知期望控制输入ud满足:

使得


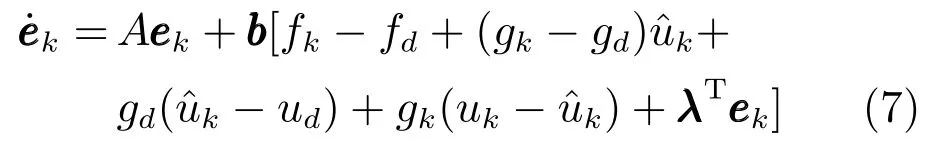
为了实现上述控制目标,本文设计重复学习控制算法以处理式(7)中的不确定性.文中对未知期望控制输入ud进行估计,得到;分析非线性项,针对其界函数的平方设计学习律,以估计值修正控制输入uk.第2节设计重复控制算法,给出该算法稳定性与收敛性分析;第3节通过仿真算例及电机实验结果表明该控制算法的有效性.
2 RLC的设计与分析
针对系统(2),设计带死区修正的学习律,估计非线性不确定性的界函数,进一步,以获得的估计值设计重复学习控制器,从而实现跟踪误差收敛于给定的邻域.
定义死区函数
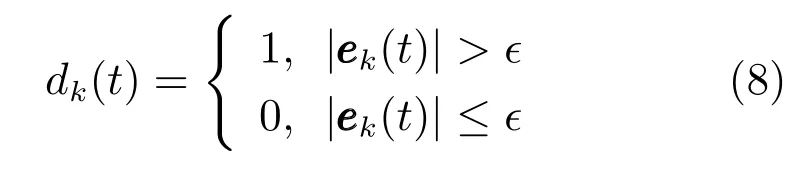
其中,为给定常数.
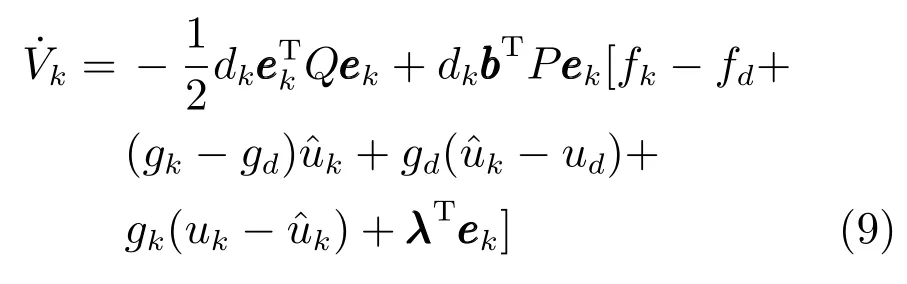
依据假设2,整理式(9)得
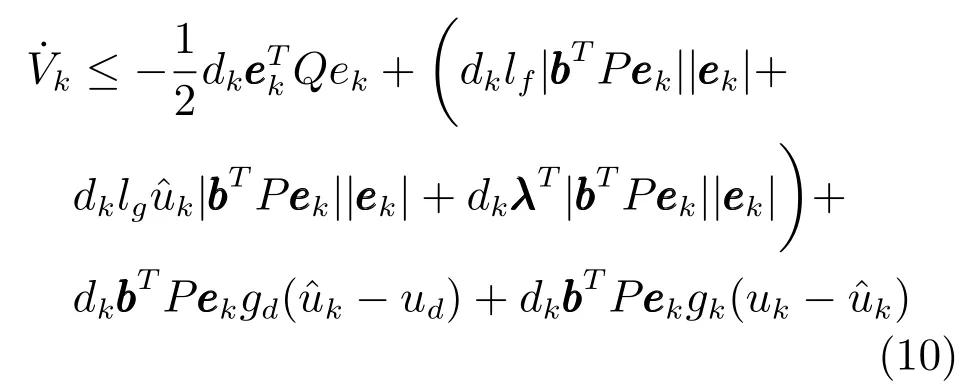
其中,lf,lg为未知参数.
基于式(10),设计如下控制律
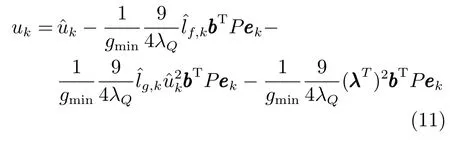
设计如下学习律
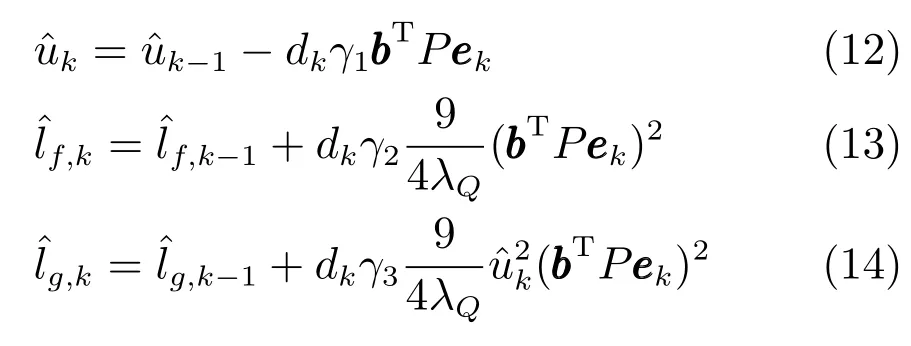
注3.设计带死区修正的学习律(12)~(14),1)避免了系统在有限时间运行后,跟踪误差在零点附近不断累加导致被学习参数发散;2)当跟踪误差进入误差带后,将不再进行参数估计.
注4.文献[20]中对于满足Lipschitz条件的非线性函数,要求其界函数已知,但实际系统往往难以精确获得其界函数,这将影响系统的控制性能.本文通过带死区修正的学习律(13)和(14)对该界函数的平方进行估计,使得所设计的控制算法较少地依赖于系统本身,从而更适合应用于实际系统.
将式(11)代入式(10)得:


因此,L0(t)在t∈[0,T]上有界,由式(22)知Lk(T)有界,根据Lk(t)定义知,有界.由式(21)知:
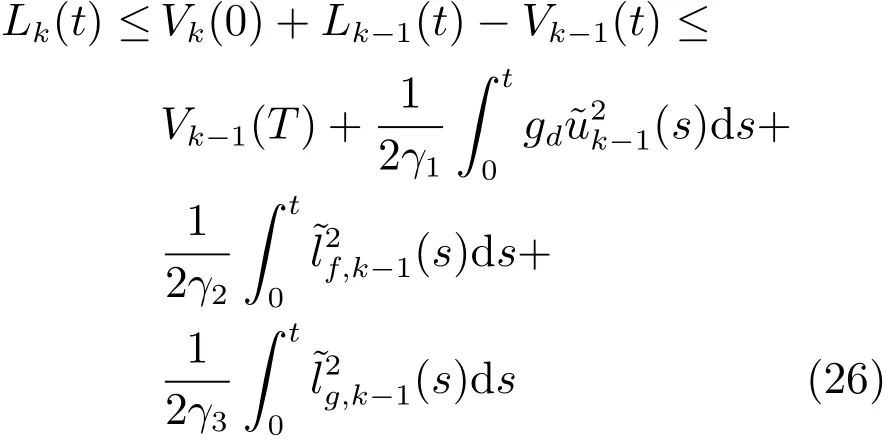
因此,∀k={0,1,2,···},Lk(t) 在t∈[0,T]上有界;由Lk(t)的定义知,Vk(t)在t∈[0,T]上有界;由Vk(t)的定义知,ek(t)在t∈[0,T]上有界.
由式(22)知,对于任意K>1,

注5.定理1对界函数的平方及期望控制输入ud采用带死区修正的估计律,设计重复学习控制器,在仅仅已知gmin的情况下,实现了跟踪误差收敛于邻域.
3 仿真与实验
为了验证文中提出的控制算法的有效性,第3.1节对小车倒摆系统进行仿真;第3.2节在电机平台上实现该控制算法,并给出实验结果.
3.1 仿真算例
小车倒摆系统可由系统(1)描述,其中
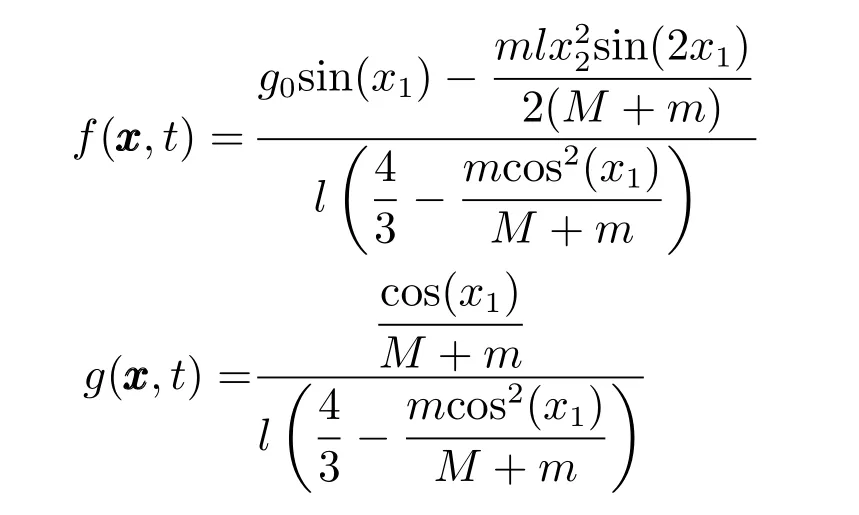
这里,n=2,x1为倒摆杆的角位移,x2为倒摆杆的角速度,u是控制输入;g0=9.8m/s为重力常数;M=1.0kg,m=0.1kg分别为小车和倒摆杆的质量;l=0.5m为摆杆长度的一半.给定参考轨迹为.系统初始状态设为x1(0)=0,x2(0)=0.2π,非线性函数g(x,t)的下界为gmin=1.39.分别选取矩阵A,Q为
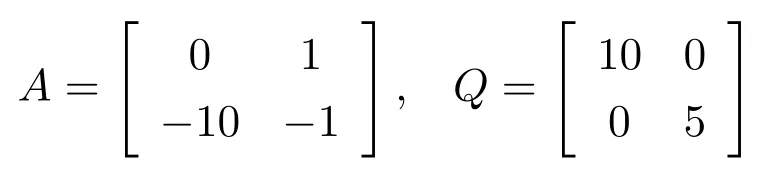
解Lyapunov方程ATP+PA=−Q得:

采用重复学习控制器(11),学习律(12)~(14),其中控制器参数分别为. 定义性能指标.系统运行28个周期,仿真结果如图1~5所示.图1刻画了性能指标Jk,由图1知随着迭代次数的增加,系统跟踪误差逐步收敛.图2给出第28次迭代的控制输入uk.图3给出参考输入的估计的变化过程.图4与图5分别为界函数平方的估计在28 次迭代中的变化情况.

图1 误差性能指标JkFig.1 Error performance indexJk
3.2 实验结果
交流电机实验平台,包括旋转电机(APMSBN01AGN,额定功率100W,额定电压200V,额定转速3000r/s);光电增量编码器(分辨率24000线/转);智能伺服驱动(ELMO HAR-5/60-3);DSP控制器(SEED-DEC2812V2.1开发板)及上位机(DELL计算机).上位机通过CCS STUDIO将编译好的程序下载至DSP开发板,通过D/A模块转换为伺服驱动ELMO所需的模拟信号(±10V电压),将该模拟信号传入ELMO驱动器获得PWM三相电压驱动电机,同时ELMO通过光电增量编码器接收电机信号,将该信号通过反馈通道输出至DSP开发板形成闭环控制系统.

图2 第28次迭代的控制输入ukFig.2 The control inputukat the 28th iteration
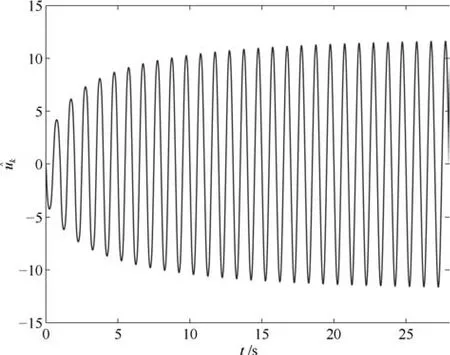
图3 参考输入估计kFig.3Estimatek

图4 界函数估计f,kFig.4 Estimate of the bound functionf,k
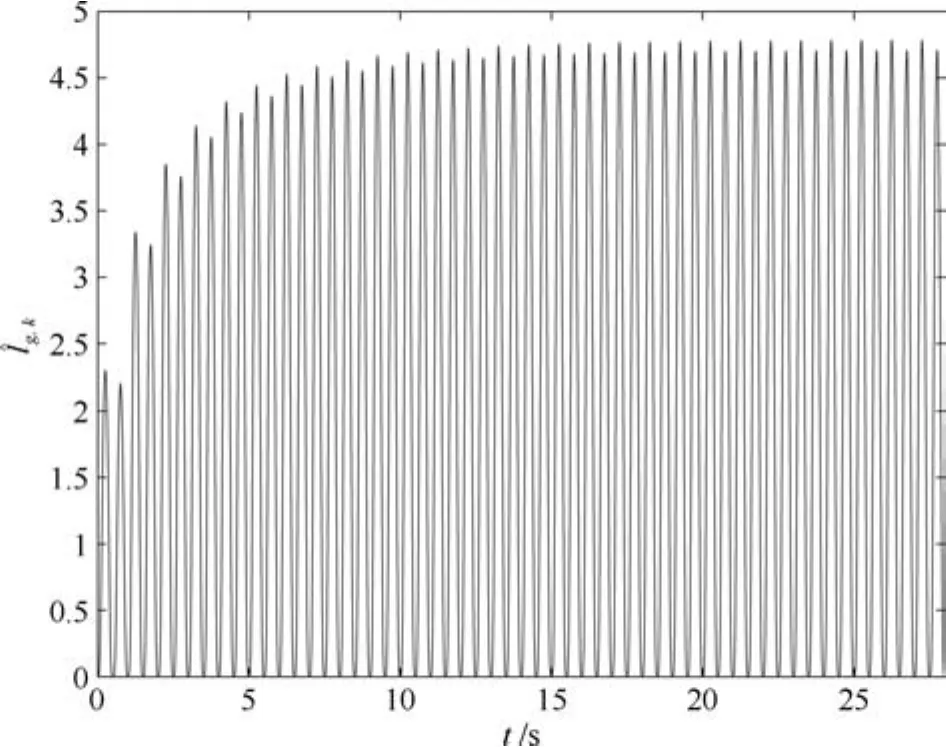
图5 界函数估计ˆlg,kFig.5 Estimate of the bound functionˆlg,k
给定参考轨迹

其中,正弦信号的频率f=2Hz.分别选取矩阵A,Q为

解Lyapunov方程得:

采用控制律(11),学习律(12)~(14),其中参数分别为,采样时间t=1ms.定义,其中c=0.01.实验结果如图6~11所示.
图6刻画了位置跟踪误差的性能指标在17次迭代过程中的变化情况,在第14次迭代以后误差保持在0.3邻域内.图7给出系统的位置跟踪误差.图8为控制输入uk.图9描述了参考输入的估计,由图8和9知,随着迭代次数的增加,逐步逼近控制输入uk.图10和11分别给出界函数平方的估计.由实验结果知,针对交流电机采用重复学习控制律,随着迭代次数的增加,能够保证跟踪误差收敛于死区界定的邻域.
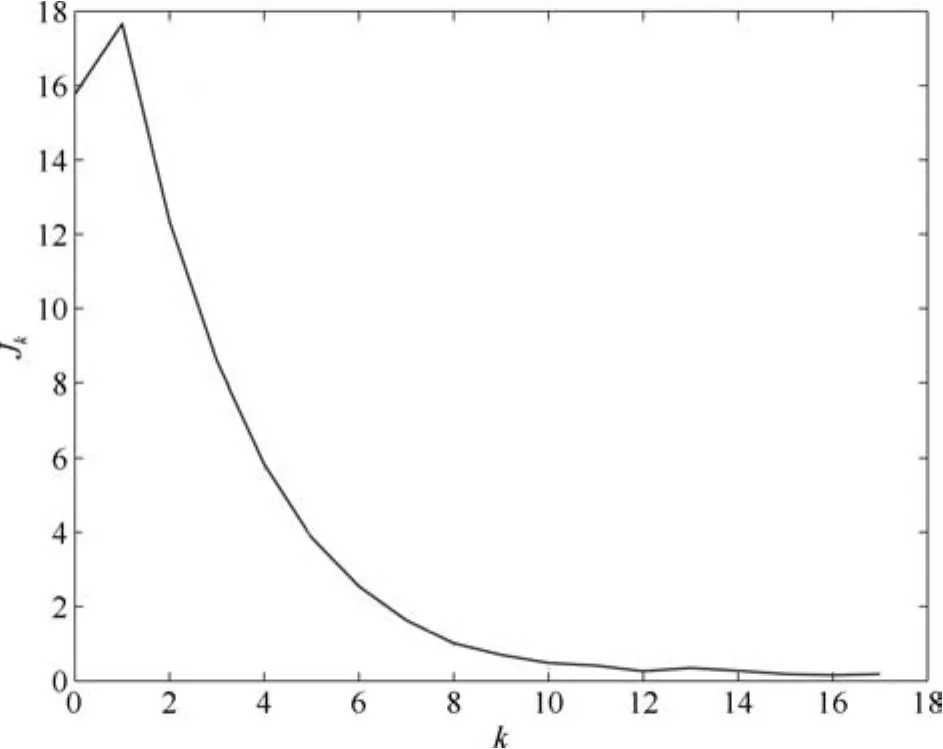
图6 误差性能指标JkFig.6 Error performance indexJk
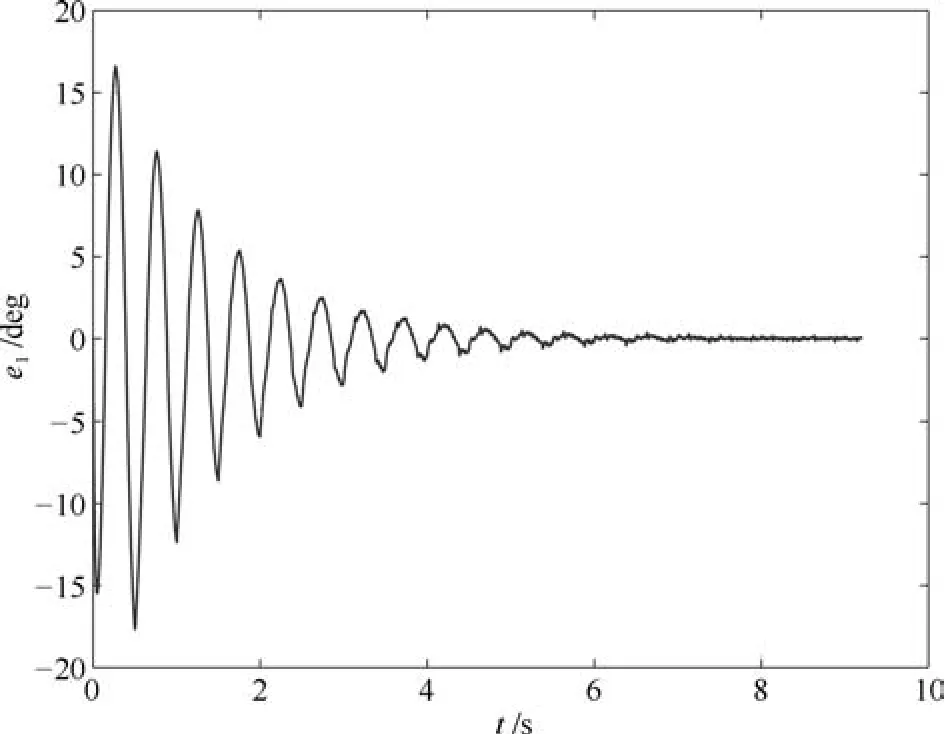
图7 位置跟踪误差e1Fig.7 Position tracking errore1
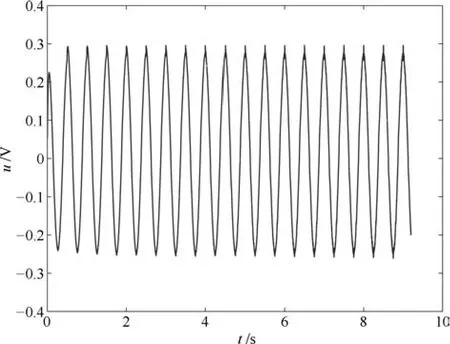
图8 控制输入ukFig.8 Control inputuk

图9 参考输入的估计kFig.9Control inputk

图10 界函数估计f,kFig.10 Estimate of the bound functionf,k
为了进一步说明本文所提方法的有效性,下面采用文献[20]中所提方法设计控制器(31),并给出对比的实验结果.

设计期望控制的学习律为
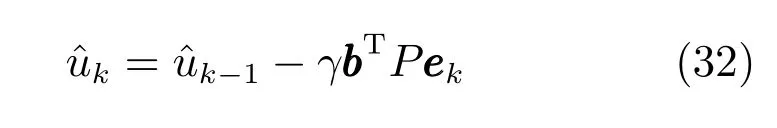
选用参考轨迹(28),采样时间为1ms.选取式(29)中的矩阵A,Q,则矩阵P为式(30).
2)选取不同的gmin进行对比.控制器(31)的参数为,1250,1500;基于重复学习方法所设计的控制器(11) 的参数为.实验结果如图15~17所示.
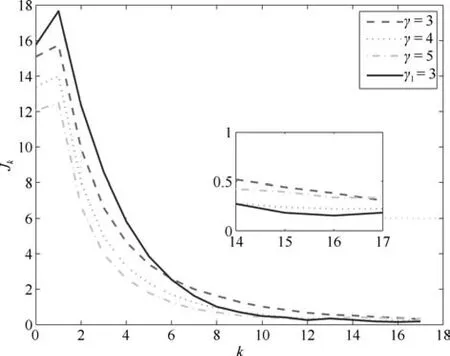
图12 误差性能指标Jk(其中三条虚线为控制器(31)的实验结果,实线为控制器(11)的实验结果)Fig.12 Error performance indexJk(the three dotted lines are the result by controller(31),the solid line is the result by controller(11))

图13 控制输入uk(其中三条虚线为控制器(31)的实验结果,实线为控制器(11)的实验结果)Fig.13 Control inputuk(the three dotted lines are the result by controller(31),the solid line is the result by controller(11))
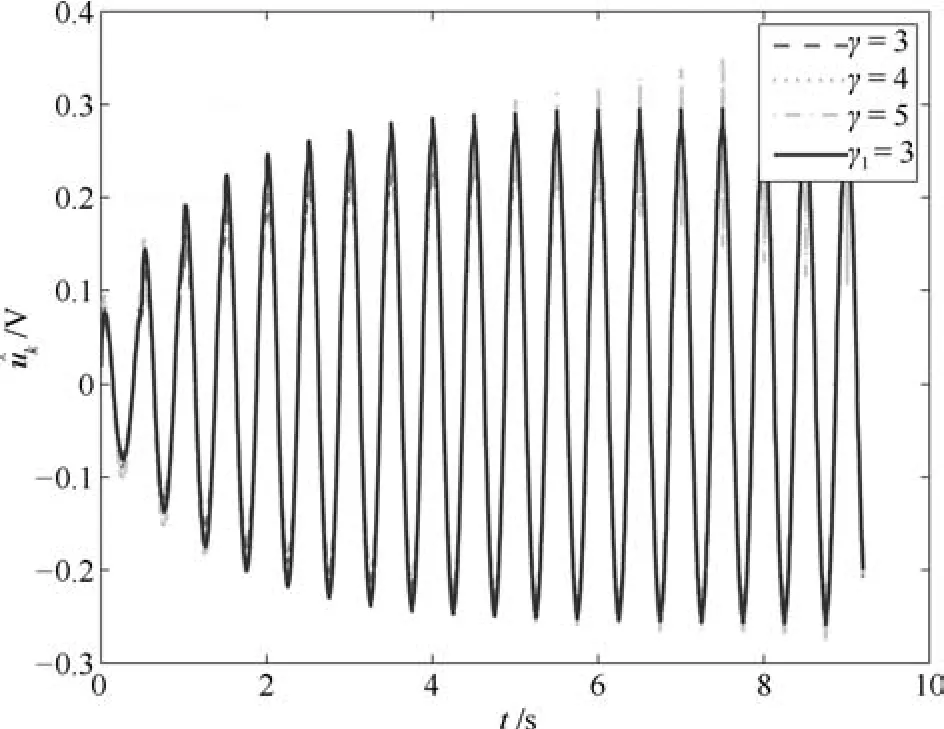
图14 参考输入的估计k(其中三条虚线为控制器(31)的实验结果,实线为控制器(11)的实验结果)Fig.14Control inputk(the three dotted lines are the result by controller(31),the solid line is the result by controller(11))
由图12与图15可以看出,文献[20]所提的控制方法与本文所设计的控制方法,均可用于处理非线性系统存在的非参数不确定性,实现跟踪误差在有限时间区间上的收敛.本文所设计的控制器(11),在仅已知gmin的情况下,并且不使用高控制增益与较大的先验值gmin时,与控制器(31)相比,具有较好的跟踪精度.图13和14,图16和17分别给出控制输入uk及其估计k的变化过程.由图12、图15知,当控制器(31)的控制增益γ与gmin分别增大时,其跟踪误差逐渐减小,然而图13和14表明,其控制输入逐渐发散.
实验结果表明,本文给出的重复学习控制算法,在仅已知控制输入增益的最小值gmin的情况下,尽可能少地依赖于系统模型,并且获得了良好的控制性能,这一结果进一步验证了该方法的有效性.
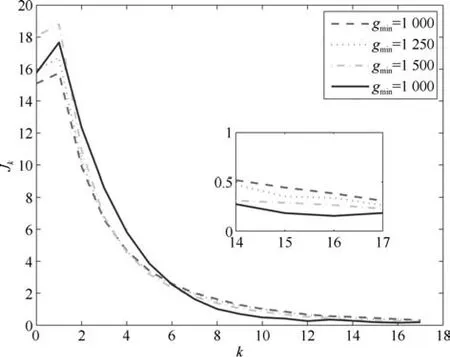
图15 误差性能指标Jk(其中三条虚线为控制器(31)的实验结果,实线为控制器(11)的实验结果)Fig.15 Error performance indexJk(the three dotted lines are the result by controller(31),the solid line is the result by controller(11))
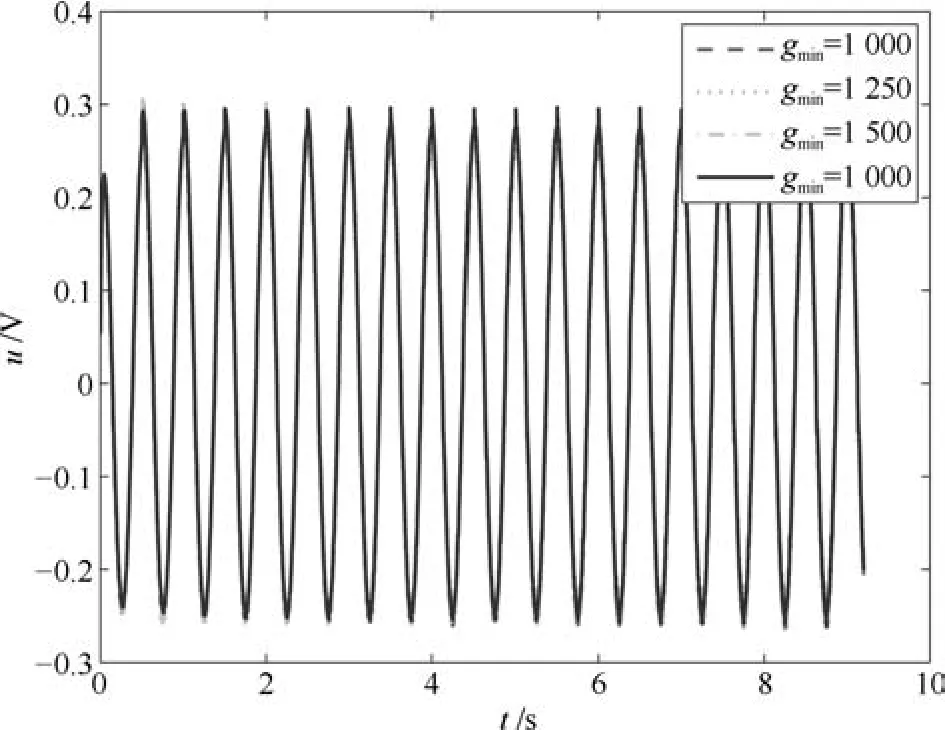
图16 控制输入uk(其中三条虚线为控制器(31)的实验结果,实线为控制器(11)的实验结果)Fig.16 Control inputuk(the three dotted lines are the result by controller(31),the solid line is the result by controller(11))
4 结论
本文研究一类不确定非线性系统的非参数不确定性问题,并基于Lyapunov分析方法设计控制器.为了处理满足Lipschitz条件的非参数不确定性,提出一种重复学习控制算法.该算法较少地依赖于系统模型,在仅已知控制输入增益最小值gmin的情况下,通过对满足Lipschitz条件的界函数进行估计,处理系统存在的非参数不确定性.文中采用带死区修正的学习律,以避免参数的正向累加影响系统的收敛性.同时,本文设计带死区的Lyapunov函数,以保证跟踪误差收敛于给定的邻域及闭环系统所有信号的有界性.此外,该控制方法能够处理与状态有关的非线性控制增益.进一步,通过仿真与实验结果,验证了本文所提控制方法的有效性.
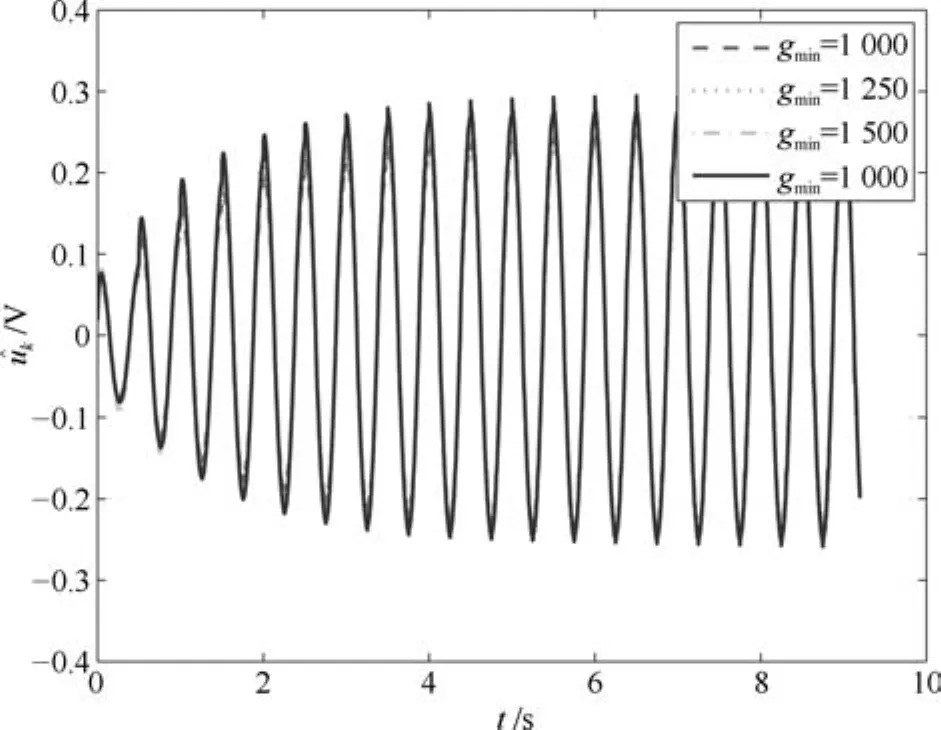
图17 参考输入的估计k(其中三条虚线为控制器(31)的实验结果,实线为控制器(11)的实验结果)Fig.17Control inputk(the three dotted lines are the result by controller(31),the solid line is the result by controller(11))

