基于通用背景−联合估计(UB-JE)的说话人识别方法
汪海彬 郭剑毅 毛存礼 余正涛
语音是人们用来交流和沟通的最自然、最直接的方式之一,因此,语音是一种重要的生物特征.作为一种重要的身份鉴定技术,目前说话人识别[1−2]已广泛运用于国家安全、司法鉴定、电话银行及门禁安全等领域.与此同时,说话人识别仍有许多问题需要解决,例如信道多样化的识别、噪声对识别性能的影响等,这就涉及到对说话人识别算法的研究.
2000年左右,Reynolds等[3]提出的高斯混合模型–通用背景模型 (Gaussian mixture modeluniversal background model,GMM-UBM),以其特有的良好性能和灵活的模型结构,降低了说话人模型对训练集的依赖,迅速成为当时说话人识别领域的主流方法之一,推动了整个领域的发展[4−5].由GMM-UBM 的思想可知,在高斯混合函数的均值超向量(Gaussian mixture model supervector,GSV)中包含有说话人语句的所有信息.根据该思想,Kenny等[6−7]提出了联合因子分析方法(Joint factor analysis,JFA),认为说话人语句中包含说话人信息和信道信息两部分,因此,GSV又可被分解为说话人和信道两部分.Dehak[8]研究发现,在对JFA进行信道补偿时,信道空间存在掩盖和重叠问题,信道空间中不可避免地包含了一部分说话人的信息,即不能准确地对说话人与信道分别建模.在此基础上,Dehak等[9−11]提出了i-vector方法,该方法认为对GSV进行处理时不应该区分说话人和信道,而应该把它们看成一个整体,即总变化空间.但是,在总变化空间中存在信道失配问题,Dehak等[9]又提出了一些信道补偿技术:线性鉴别分析(Linear discriminant analysis,LDA)和类内协方差规整(Within class covariance normalization,WCCN)等.近几年来,基于i-vector方法的说话人识别模型(图1)明显提升了说话人识别系统的性能,是目前说话人识别领域中最热门的建模方法之一[12−13].在美国国家标准技术局组织的说话人评测(The National Institute of Standards and Technology speaker recognition evaluation,NIST SRE)中,该方法的性能明显优于GMM-UBM[3]和GSV-SVM(Gaussian mixture model supervectorsupport vector machine)[14−15]等方法,是处于国际研究前沿的一种说话人识别方法.
i-vector是一种有效的因子分析方法,其中总变化因子空间的估计是基础和关键.为了得到性能更好的i-vector方法,本文结合常规的因子分析方法提出了一种新的总变化因子空间估计算法,即通用背景–联合估计(Universal background-joint estimation algorithm,UB-JE)算法.首先,针对说话人识别任务中正负样本分布不平衡问题,本文借鉴GMM-UBM 的思想,结合i-vector方法,通过大量的非训练数据来训练形成一个包含大量说话人的通用背景初始总变化空间,从而提出了总变化矩阵通用背景(Universal background,UB)算法;其次,在i-vector模型中由于均值不能很好地与更新后的总变化因子空间耦合,我们根据因子分析理论结合文献[16−17]提出了一种总变化矩阵联合估计(Joint estimation,JE)算法;最后,将两种算法相结合得到通用背景–联合估计(UB-JE)算法.
本文结构如下:第1节介绍了因子分析方法的理论,主要是高斯混合模型超向量、联合因子分析方法和总变化因子分析方法;第2节提出通用背景–联合估计总变化矩阵估计算法,包含两种总变化因子空间估计算法,即通用背景算法和联合估计算法;第3节是针对提出的三种总变化因子空间估计算法的实验与结果分析;第4节是结论.
1 因子分析方法理论
1.1 高斯混合模型超向量
由于GMM-UBM[3]是先用一些无关数据训练一个通用背景模型(Universal background model,UBM),然后利用训练数据对该UBM 进行数据更新,得到代表单个说话人的高斯混合模型(Gaussian mixture model,GMM).按照GMM-UBM 模型的原理,说话人所有的语音信息都包含在由说话人GSV[14−15]中(GSV形成过程见图2).一般情况下,在说话人识别领域里常用的超向量是均值超向量,因此,下文中的超向量如果没有特别指明,均默认为均值超向量.
1.2 联合因子分析方法
随着科技的发展,语音可以通过多种渠道获取,在说话人识别任务中相应地产生了信道失配问题.Kenny等[6−7]认为一段语音信号中应包含说话人信息和信道信息两部分,因此对说话人进行识别时,GSV应该被分解为说话人和信道两部分,分别对它们建立模型,然后去除无关信息(信道模型),留下有用信息(说话人模型),然后再进行估计,这就是JFA的思想.

图1 i-vector说话人识别系统Fig.1 i-vector speaker recognition system
根据Kenny提出的JFA思路,假设有一个混合度为C的GMM-UBM 模型,训练时的语音特征参数为F维,则形成一个FC维的均值超向量,则该超向量可表示为


图2 GMM均值超向量的形成过程Fig.2 The formation process of GMM mean super vector
其中,ms,h为特定说话人s的第h段语音所形成的FC×1维的GSV,mu是FC×1维的UBM超矢量,U表示信道空间,是一FC×Ru维矩阵,其中Ru为信道因子数,V表示说话人空间,是一FC×Rv维矩阵,Rv是说话人因子数,D是残差空间,是一个FC×FC维的对角矩阵,xs,h表示信道因子,ys表示说话人s的因子,zs是残差因子.一般来说,10 由式(1)可知,在JFA中需要对mu,U,V以及D进行预先估计,由于mu已预先得到,因此只需要估计其他三个矩阵,即λ=(U,V,D).关于这三个矩阵的估计参见文献[16]. 由于JFA存在空间掩盖和空间重叠问题[8],不能很好地区分说话人和信道.Dehak等提出了ivector[9−10],i-vector把说话人和信道看成一个整体,根据JFA可把i-vector表示为 其中,s为特定说话人GSV,m为UBM超矢量,T表示总变化因子空间,迭代更新时,先随机初始化,w为总变化因子,即i-vector,ε为残差. 其中,Σ为对角协方差矩阵,可用UBM 协方差代替. 由式(2)可知,i-vector的建模可简化为对模型参数λ=(s,m,T,Σ)的估计,由上述理论可知,训练数据的s,m很容易得到,因此,可简化为对λ=(T,Σ)的估计.其中最关键的是对总变化因子空间T的估计,T的估计类似于JFA中说话人空间估计,可以采用最大期望(EM)算法得到,参见文献[9].步骤如下: 步骤1.估计统计量.一段语音特征参数为xs,t,UBM 超矢量为m,则 其中,Nc,s为零阶统计量,Fc,s为一阶统计量,Sc,s为二阶统计量,mc为m中的第c个分量,γc,s,t为第c个高斯密度函数后验概率. 步骤2.(E步)计算总变化因子w的一阶统计量和二阶统计量. 其中,Ls为临时中间变量,为w的一阶统计量(需要的结果)和二阶统计量,Ns为Nc,s的对角拼接FC×FC维矩阵,Fs为Fc,s拼接的FC维矢量,Σ为UBM协方差. 步骤3.(M步)更新T和Σ. T更新: Σ更新: 其中,Ss为Sc,s拼接的FC×FC维矩阵,N=为所有说话人零阶统计量之和.(当反复迭代几次后,就可得到收敛的T和Σ). 在i-vector中T的估计是关键和基础,由上一节可知,T是通过随机初始化然后通过迭代产生的,但并没有考虑到通用背景的情况.本文根据GMMUBM的思想,先通过背景无关数据产生一个初始化的Tubm,然后再进行迭代更新,提出了一种总变化因子空间通用背景算法.在常规的i-vector算法中,用均值最大化算法(Expectation maximum,EM)对数据更新时,仅仅考虑到T和Σ,而没有对m进行更新.为了使得i-vector能够有更好的结合性,本文又提出了一种同时更新m和T的联合估计算法.在本节最后,我们把上述两种算法相结合,提出通用背景–联合估计算法. 首先,利用大量的无关数据训练一个UBM 超向量,并根据i-vector中T估计方法估计一通用背景变化空间Tubm.然后,将Tubm作为EM 算法中对T估计的初始矩阵,进行自适应计算(如图3所示).具体如下: 图3 总变化因子的常规估计算法和UB算法(虚线框)比较Fig.3 Comparison of conventional estimation algorithm of total variation factor with UB(dashed frame) 步骤1.通过前端处理将大量的无关数据训练成一个UBM超向量,并结合第1.3节中T的估计算法,生成一个通用背景下的总变化空间,记为Tubm. 步骤2.将Tubm代入式(7),生成Ls. 步骤3.将Ls代入式(8)和式(9)生成E[ws]和E[wswTs]. 步骤4.结合Tubm,E[ws]以及E[wswTs],根据第1.3节中的EM算法,依次对T和Σ进行更新. 步骤5.观察T和Σ是否收敛或者达到迭代次数.如果没有,则返回步骤2继续;否则退出. 由第1.3节可知,i-vector的建模可转化为对λ=(s,m,T,Σ)的估计.其中,s与m已预先估计好了,即GSV和UBM超矢量,因此,只更新λ=(T,Σ).事实上,在更新T和的Σ的同时,也应该更新m,即λ=(m,T,Σ),只有这样,不断更新的参数模型才会更加耦合. 本文提出一种m,T联合估计算法,即 把T和m看成一个整体,在更新T的同时,也更新m.此时,i-vector模型表示为λ1=(T1,Σ),根据式(2)可写为 其中,s为GSV,w1=[wT1]T,称为联合变化因子,T称为联合变化空间,ε为残差. 根据第1.3节中i-vector中的EM更新算法可得: 步骤1.(E步) 步骤2.(M步) 对T1更新: 对Σ更新: 对T1的更新就是对T和m同时更新. 基于上述两种算法,本文将它们相结合形成互补,提出了一种新的算法,即UB-JE(如图4所示).具体如下: 步骤1.通过大量无关数据得到UBM超向量,集合JE算法中T1的估计算法,得到通用背景–联合总变化空间T1ubm. 步骤2.将T1ubm代入式(15),生成Js. 步骤3.将Js代入式 (16)和式(17),生成E[w1s]和E[w1sw1Ts]. 步骤4.结合T1ubm,E[w1s]以及E[w1sw1Ts],根据JE算法中的EM算法,依次对T1和Σ进行更新. 步骤5.观察T1和Σ是否收敛或者达到迭代次数.如果没有,则返回步骤2继续;否则退出. 图4 通用背景–联合估计算法(虚线框)Fig.4 Diagram of universal background-joint estimation algorithm(dashed frame) 实验的测试数据采用TIMIT语音库[18]、MDSVC语音库[19]以及一组由MDSVC语音库组成的长时语音数据.实验在预处理阶段包括:有效语音端点检测(短时能量与平均过零率相结合的方法)、预加重(因子为0.95)、分帧(帧长25ms,帧移12.5ms)和加窗.实验采用39维美尔倒谱系数(Mel frequency cepstral coefficients,MFCC)特征参数(基本特征包括1维能量和12维倒谱、13维一阶差分特征以及13维二阶差分特征).实验中,UBM混合数为512,密度函数方差采用对角矩阵.在i-vector训练中,总变化因子空间维数设置为400,训练时迭代次数取6次. 运用5300句TIMIT语音(女性1620句语音,男性3680句语音)、MDSVC中Enroll_Session1+Enrol_Session2以及用HTK工具[20]对MDSVC语音数据组合长句(48Enroll_Session1+48Enroll_Session2+40Imposter共136长句)分别训练UBM模型和T.实验训练数据为100人(30个女性,70个男性,每人9句语音)TIMIT语音、MDSVC中Imposter(23个文件的男性和17个文件的女性中各50句)以及MDSVC中部分数据(30个文件的男性和30个文件的女性中各50句);测试数据为TIMIT中100人(30个女性,70个男性,每人1句语音)、MDSVC Imposter(23个文件的男性和17个文件的女性中的剩余4句)以及MDSVC中部分数据(30个文件的男性和30个文件的女性中各4句)(详见表1).本文设置了一个基线实验(GMM-UBM)[3]来验证因子分析方法(i-vector)的有效性. 表1 实验所用语音库Table 1 The corpus used in the experiment 本文采用等错误率(Equal error rate,EER)和2010年的NIST SRE中的最小检测代价函数(Minimum detection cost function 2010,Min-DCF10)[21]作为性能评测指标.MinDCF10与EER越小说明系统的性能越好. 检测代价函数计算公式为 表2 MinDCF10参数设定Table 2 MinDCF10 parameter setting 为了验证所提算法的有效性,本文基于两种不同的语音库设置了四个实验:实验1基于TIMIT语音库;实验2基于MDSVC语音库;实验3是在两者综合的语音库中完成的;实验4基于MDSVC语音库组成的长时语音数据.每一个实验做6次比较试验,即基线实验(GMM-UBM)[3]、本文提出的三个新算法、总变化矩阵传统算法以及文献[22]中i-vector矢量规整PLDA技术.由于不同语音库的录音条件、方式等不同,四个实验分别代表了四种不同的实验环境.表3~6分别给出在不同语音库上各算法训练T后的系统性能比较.表中括号里的是性能提升值. 表3 GMM-UBM、传统算法估计T、本文所提出算法估计T以及PLDA在TIMIT语音库上的性能对比Table 3 Performance comparison of GMM-UBM,the traditional algorithm to estimateT,the proposed algorithms to estimateT,and the PLDA on TIMIT corpora 表4 GMM-UBM、传统算法估计T、本文所提出算法估计T以及PLDA在MDSVC语音库上的性能对比Table 4 Performance comparison of GMM-UBM,the traditional algorithm to estimateT,the proposed algorithms to estimateT,and the PLDA on MDSVC corpora 表5 GMM-UBM、传统算法估计T、本文所提出算法估计T以及PLDA在TIMIT+MDSVC语音库上的性能对比Table 5 Performance comparison of GMM-UBM,the traditional algorithm to estimateT,the proposed algorithms to estimateT,and the PLDA on TIMIT mixed MDSVC corpora 表6 GMM-UBM、传统算法估计T、本文所提出算法估计T以及PLDA在MDSVC长句语音库上的性能对比Table 6 Performance comparison of GMM-UBM,the traditional algorithm to estimateT,the proposed algorithms to estimateT,and the PLDA on MDSVC long sentence corpora 为了更加直观地观察实验结果,本文分别作了图5和图6.图5是在不同语音库中各个算法的性能比较(表3∼6的内容),图6是不同算法在四种语音库中的性能比较(包含表7). 表7 通用背景–联合估计算法在不同语音库中的性能对比Table 7 Performance comparison of universal background-joint estimation algorithm on different speech corpus 从以上图表可以看出,在TIMIT数据集、MDSVC数据集、TIMIT+MDSVC综合集或MDSVC长句集上,1)因子分析方法相较于基线系统(GMM-UBM)性能都有显著提升.2)新提出算法的性能都有一定提升,特别是通用背景–联合估计算法的性能在TIMIT中提升了较为明显,EER和MinDCF10分别提升21%和24%.同时,在实验环境更加复杂的综合集TIMIT+MDSVC上性能也有一定提升,EER和MinDCF10分别提升了8.3%和6.9%.通过每单个实验的对比发现,联合估计算法的性能要一致性的优于通用背景算法,两者结合的算法(通用背景–联合估计)可以得到更优的系统.3)相比于文献[22]中i-vector矢量规整PLDA技术,本文提出的算法(UB-JE)在不同语音数据库中,性能有一定的提升. 但是对比表3~6的数据可知,表6中算法的性能最好,其次是表3,然后是表4,最后才到表5(从表7和图6可以看出),这是由于长时语音相对短时语音更能准确地代表说话人信息以及随着语音数据复杂程度的提高,系统的性能受到一定的影响.现阶段说话人识别领域一个热门方向就是针对语音数据复杂程度展开的,即多信道下的说话人识别,这是说话人识别发展的一个趋势. 图5 不同语音库中各算法性能对比Fig.5 Performance comparison of algorithms on different speech corpus 图6 不同算法在四种语音库中的性能对比Fig.6 Performance comparison of different algorithms on four speech corpus 本文主要研究了说话人识别算法i-vector中总变化因子空间T的估计,提出了四种T估计算法.实验结果显示,在三种语音库中,新提出的三种算法对系统的性能都有一定的提升(如图5),且不同语音库对每一种算法的性能都有一定的影响(如图6).实验结果证明有效估计T对整个i-vector模型起着至关重要的作用,验证了前面i-vector理论分析,T的估计引领着整个模型.语音库的选择对整个系统的性能有一定影响,下一步将在更加复杂的语音库(如NIST SRE语音库)上进行评测实验.1.3 总变化因子分析方法

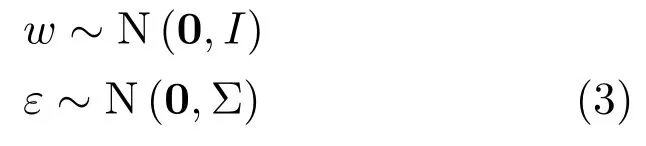
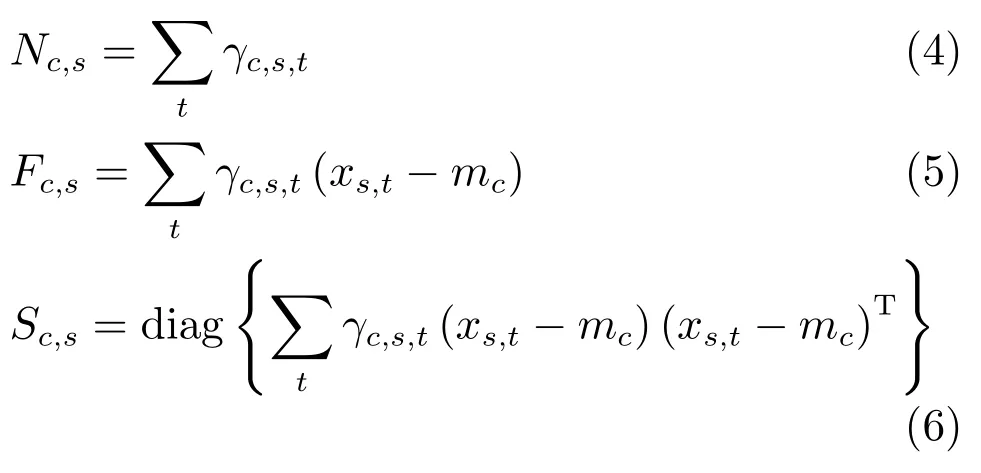

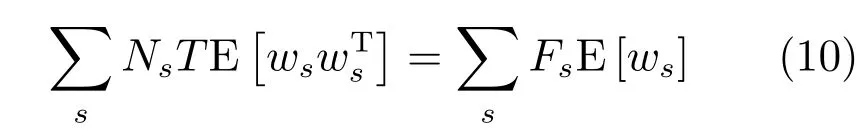
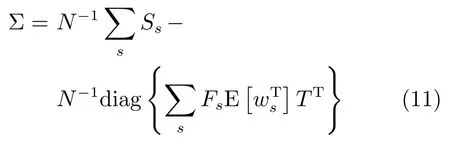
2 总变化因子空间通用背景−联合估计算法
2.1 通用背景算法(UB)
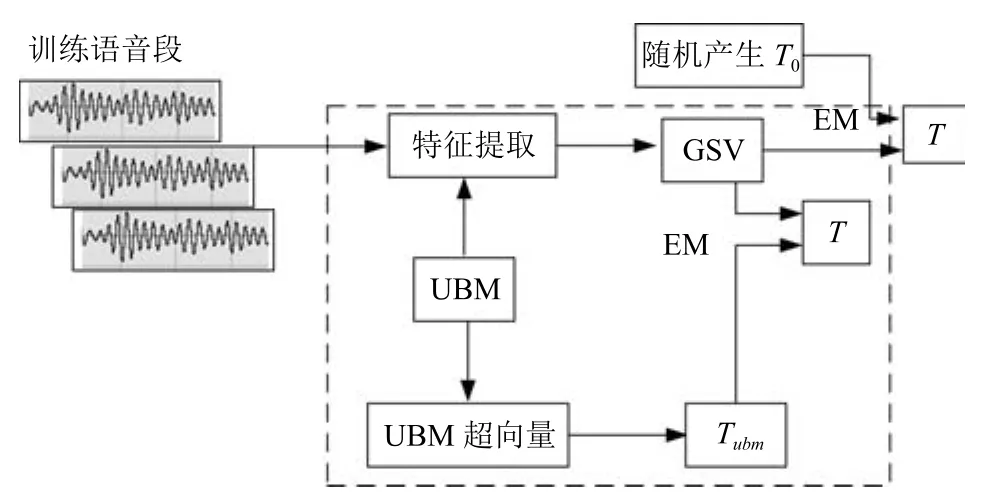
2.2 联合估计算法(JE)

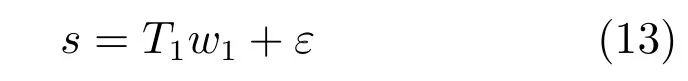
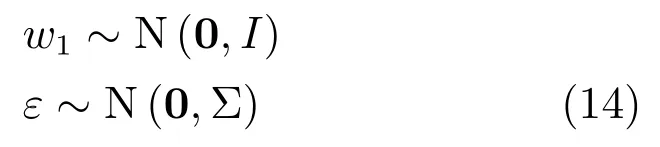

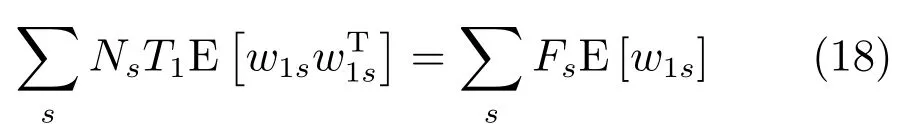

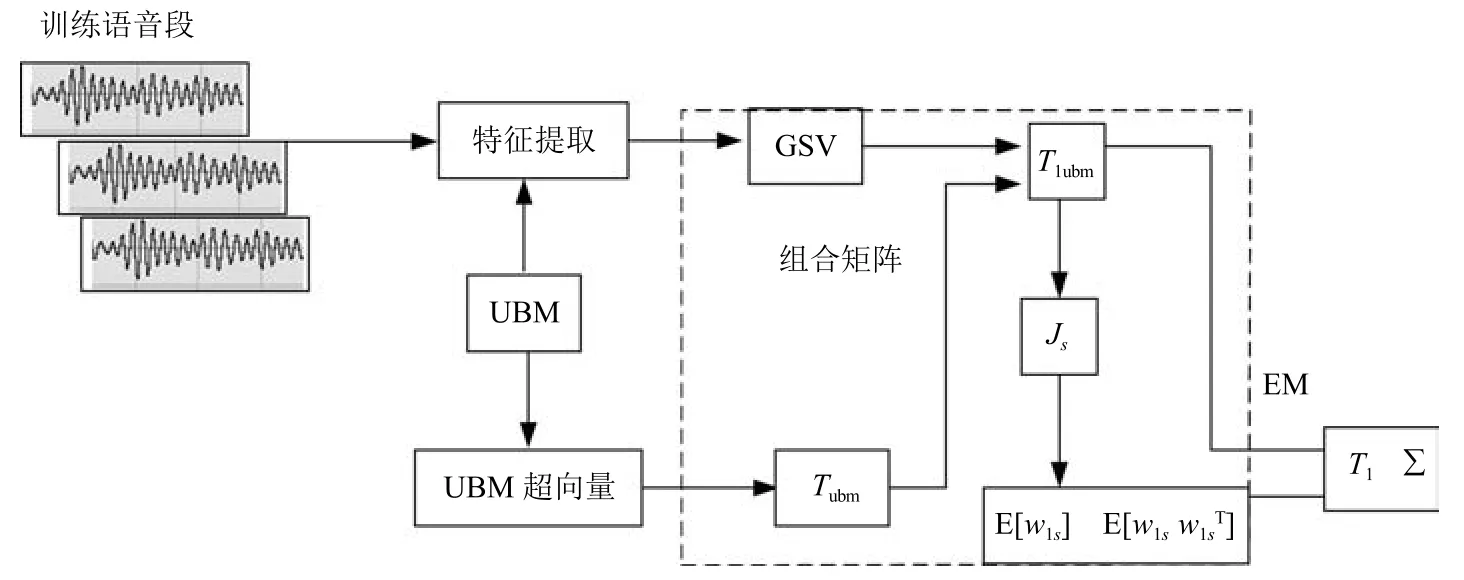
2.3 通用背景−联合估计算法(UB-JE)
3 实验与分析
3.1 实验设置

3.2 评价指标


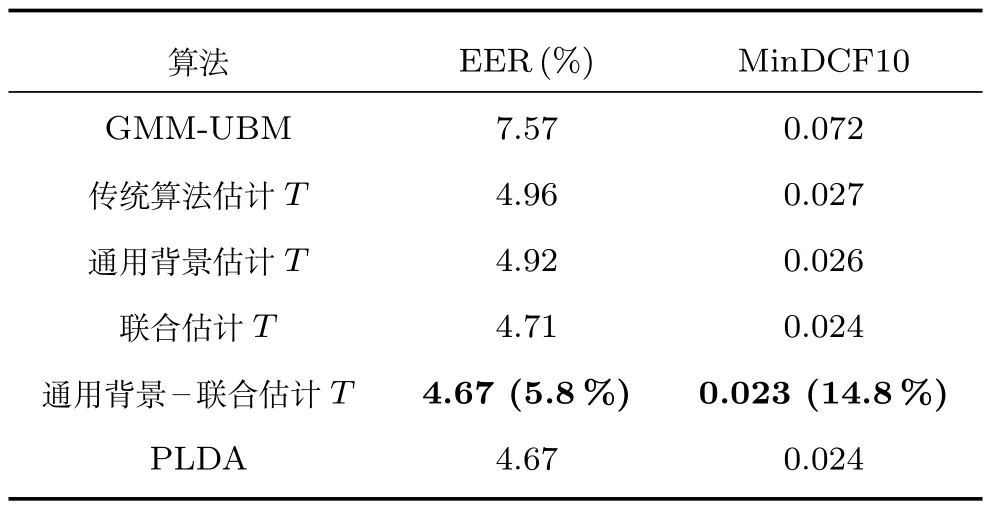
3.3 实验设计与结果分析






4 结论

